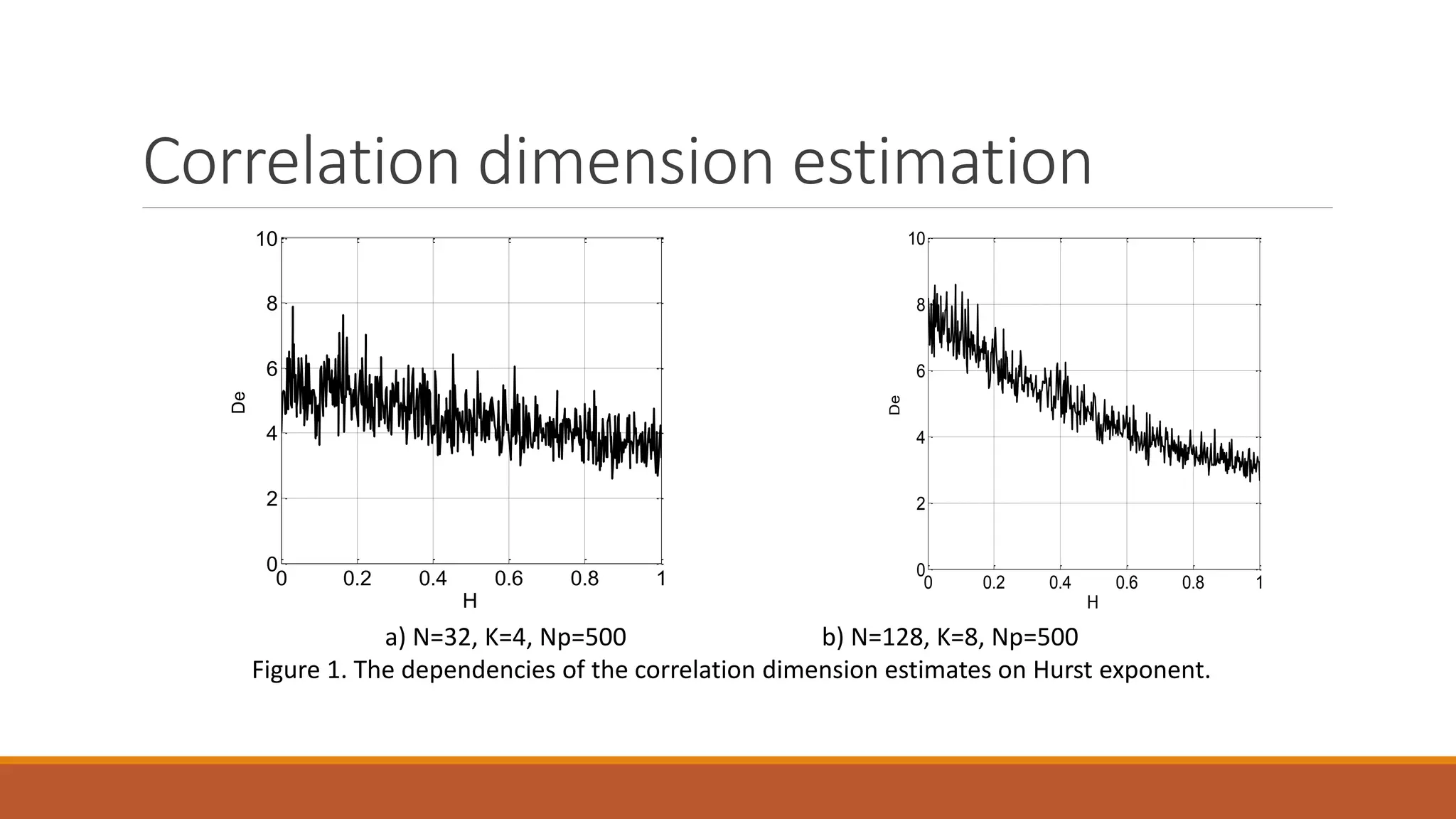
This document proposes two adaptive scanning methods for optimally scanning Gaussian and fractal Brownian images and estimating their correlation dimension. The first method chooses the scanning direction based on the criterion of maximum correlation coefficient between subsequent pixels. The second method chooses the direction based on maximum scalar product between the previous and following vector. Both methods are evaluated on test images and are shown to produce optimal scanning trajectories that take advantage of correlations in the images. Estimation of correlation dimension using the scanning methods is also demonstrated to simplify object detection problems.

1. Optimal Scanning of Gaussian
and Fractal Brownian Images
with an Estimation of
Correlation Dimension
A.Yu. Parshin, PhD,
Prof. Yu.N. Parshin, Doctor of Technical Sciences
Ryazan State Radio Engineering University, Ryazan, Russia
parshin.y.n@rsreu.ru

2. Already known scanning methods
Static scanning methods
◦ Usual scanning methods – vertical, horizontal, diagonal.
◦ Space-filling curves – Peano-Hilbert curves.
Adaptive scanning methods
◦ Choosing scanning method for every image.
◦ Calculation of information parameter and considering it as criterion of scanning direction.

3. Calculation of correlation dimension
Usage of time-delayed values of observable component as values of non-observable components:
Distances between vectors (DE=3):
              2
33
2
22
2
11 mkmkmki txtxtxtxtxtxr 
Number of vectors:
ED
N
N 
DE – dimension of space of embeddings
Ns – number of signal samples
 1,...,  EE DnDnn xxx
  12  DDE
  1 DDE
Dimension of space of embeddings is chosen according to value of object dimension D:
For specific task it is enough to use the following expression:

4. Calculation of correlation dimension
Combined probability density function of independent distances:
Combined probability density function of dependent distances from second vector to each other:
   
 










1,0,0
1,0,
|
1
1
r
r
r
D
m
M
m
rD
Dw
 
 
 
 



















.3
,,...,3,,,0
,...,3,,
,
,|
maxmin
maxmin
1
min
32
minmax
122
kNm
Nkrrr
Nkrrr
rr
rr
D
Dw
kkm
kkm
D
km
N
Nm kk
rr

5. Calculation of correlation dimension
Classic interpretation of correlation dimension:
Maximum likelihood algorithm for independent distances:
Likelihood function for dependent distances:
Maximum likelihood algorithm for dependent distances:
 


 M
m
m
DD
est
r
M
DwD
E
1
0
ln
|maxarg r
        .,|||, 1
min
32
minmax
1
1
1
1
122112112








  D
km
N
Nm kk
D
m
N
m
rr
rr
D
rDDwDwDw rrrrr
   
1
32
min
1
1
1 lnln32ˆ




 







 
N
Nm
km
N
m
m rrrND
 
r
rC
D N
nr log
log
limlim
0 


6. Correlation function of fractal Brownian
surface
The correlation of the pixels series is specified as follows:
Let us define a fractal Brownian surface as an assembly of the random values X(i,j) given on the
2D coordinate axis. A probability measure of the random value increments:
the correlation coefficient of increments equals:
        2211221121 ,,,,,, kkkkkkkks jijiRjipjipkkR  M
       jiXjjiiXjiXjiXX ,,,, 1122 
 
    1
1
,,,
2
2
1
2
1
2
12
2
12
2211












H
ji
jjii
jijir

7. Construction of fractal Brownian surface
based on correlation function
100 200 300 400 500
50
100
150
200
250
300
350
400
450
500
100 200 300 400 500
50
100
150
200
250
300
350
400
450
500
100 200 300 400 500
50
100
150
200
250
300
350
400
450
500
20 40 60 80 100
10
20
30
40
50
60
70
80
90
100
20 40 60 80 100
10
20
30
40
50
60
70
80
90
100
20 40 60 80 100
10
20
30
40
50
60
70
80
90
100
a) H=0,1 b) H=0,5 c) H=0,9
Figure 2. Image of 2D Fractal Brownian motion
a) ax=0,01, ay=0,1 b) ax= 0,1, ay= 0,1 c) ax= 0,1, ay= 0,01
Figure 3. Image of 2D Gaussian process

8. Proposed scanning methods
Algorithm 1
Scanning direction is chosen by criterion of correlation coefficient maximum of each subsequent
pixel. This method uses image characteristics, averaged by significant ensemble of samples, but
it doesn’t consider properties of particular image.
In case of image in the form of fractal Brownian surface correlation of pixels equals:
 H
x
H
xx
H
x
H
y
H
yy
H
ymn mmnnnmnnR 222222
2
,
4





 



9. Proposed scanning methods
Algorithm 2
Scanning direction is chosen by criterion of scalar product maximum of previous vector X and
following vector Y.
Steps of this algorithm:
◦ First vector consists of M image pixels from first line of current frame;
◦ One of Q predefined directions from last pixel to end of next vector is considered;
◦ standard scalar product is evaluated for pair of vectors previous X and each of Q considered directions Y
as follows:
◦ maximum value of scalar product defines a pair of vectors and thereby the direction of scan trajectory;
◦ scan trajectory moves to new pixel, which is last for chosen vector;
◦ the algorithm is repeated until majority pixels are covered.
 
YX
YX
YX


,
,R

10. Optimal scanning trajectories
0 10 20 30 40 50 60 70
0
10
20
30
40
50
60
70
0 10 20 30 40 50 60 70
0
10
20
30
40
50
60
70
10 20 30 40 50 60
10
20
30
40
50
60
10 20 30 40 50 60
10
20
30
40
50
60
Figure 4. Optimal scanning trajectory
by 1-st method, image of figure 2c
Figure 5. Optimal scanning trajectory
by 2-st method, image of figure 2c
Figure 6. Optimal scanning trajectory
by 1-st method, image of figure 3a
Figure 7. Optimal scanning trajectory
by 2-st method, image of figure 3a

11. Correlation dimension estimation
0 0.2 0.4 0.6 0.8 1
0
2
4
6
8
10De
H
0 0.2 0.4 0.6 0.8 1
0
2
4
6
8
10
De
H
a) N=32, K=4, Np=500 b) N=128, K=8, Np=500
Figure 1. The dependencies of the correlation dimension estimates on Hurst exponent.

12. Conclusion
◦ Appliance of maximum likelihood algorithm demands provision of maximum
correlations between image pixels in one-dimension sequence.
◦ Scanning by maximum correlation coefficient criterion provides bigger
difference between values of correlation dimension estimates and therefore
simplifies solution of object detection problem.

13. Thanks for Your attention!