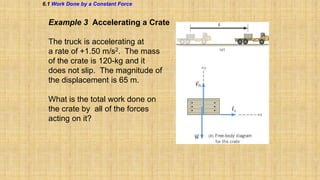
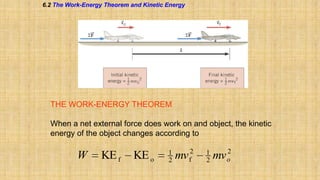
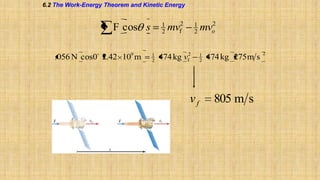
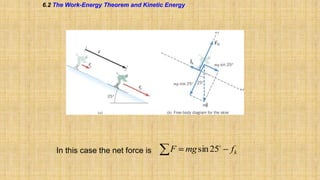
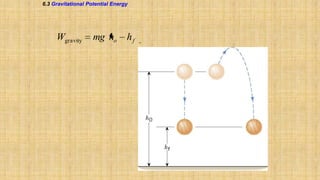
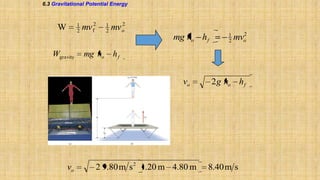
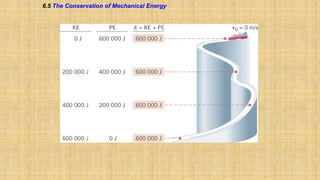
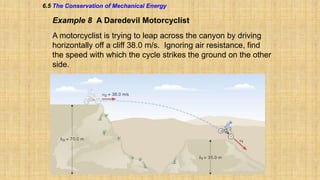
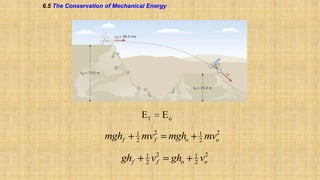
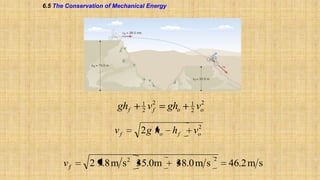
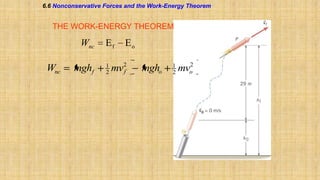
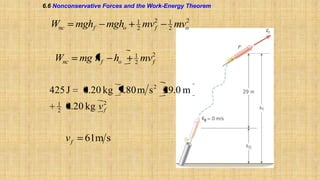
The document summarizes key concepts about work, energy, and power from physics. It defines work as force multiplied by displacement and discusses how work depends on the angle between force and displacement. It introduces the work-energy theorem which relates work to changes in kinetic and potential energy. It defines kinetic and gravitational potential energy. It discusses conservative versus nonconservative forces and how the total mechanical energy is conserved for conservative forces. It also defines power as the rate at which work is done or energy is converted. The overall document covers various forms and conversions of energy according to physics principles like conservation of energy.

1. Work done by: Mrreynon

2. Chapter 6
Work and Energy

3. 6.1 Work Done by a Constant Force
W
Fd
or
W
Fs
1 N m 1 joule J

4. 6.1 Work Done by a Constant Force
cos0 1
W
F cos s
cos90
cos180
0
1

5. 6.1 Work Done by a Constant Force
Example 1 Pulling a Suitcase-on-Wheels
Find the work done if the force is 45.0-N, the angle is 50.0
degrees, and the displacement is 75.0 m.
W
F cos s
2170 J
45.0 N cos50.0 75.0 m

6. 6.1 Work Done by a Constant Force
W
W
F cos 0 s
F cos180 s
Fs
Fs

7. 6.1 Work Done by a Constant Force
Example 3 Accelerating a Crate
The truck is accelerating at
a rate of +1.50 m/s2. The mass
of the crate is 120-kg and it
does not slip. The magnitude of
the displacement is 65 m.
What is the total work done on
the crate by all of the forces
acting on it?

8. 6.1 Work Done by a Constant Force
The angle between the displacement
and the friction force is 0 degrees.
fs
W
ma
120 kg 1.5 m s 2
180 N cos 0 65 m
180 N
1.2 10 4 J

9. 6.2 The Work-Energy Theorem and Kinetic Energy
DEFINITION OF KINETIC ENERGY
The kinetic energy KE of and object with mass
m and speed v is given by
KE
1
2
mv
2

10. 6.2 The Work-Energy Theorem and Kinetic Energy
THE WORK-ENERGY THEOREM
When a net external force does work on and object, the kinetic
energy of the object changes according to
W
KE f
KE o
1
2
mv
2
f
1
2
mv
2
o

11. 6.2 The Work-Energy Theorem and Kinetic Energy
Example 4 Deep Space 1
The mass of the space probe is 474-kg and its initial velocity
is 275 m/s. If the .056 N force acts on the probe through a
displacement of 2.42 109m, what is its final speed?

12. 6.2 The Work-Energy Theorem and Kinetic Energy
W
W
F cos s
1
2
mv
2
f
1
2
mv
2
o

13. 6.2 The Work-Energy Theorem and Kinetic Energy
1
2
F cos s
.056 N cos0 2.42 109 m
1
2
mvf2
1
2
474 kg vf2
vf
2
mvo
1
2
474 kg 275 m s
805 m s
2

14. 6.2 The Work-Energy Theorem and Kinetic Energy
In this case the net force is
F
mg sin 25
fk

15. 6.3 Gravitational Potential Energy
W
Wgravity
F cos s
mg ho
hf

16. 6.3 Gravitational Potential Energy
Wgravity
mg ho
hf

17. 6.3 Gravitational Potential Energy
Example 7 A Gymnast on a Trampoline
The gymnast leaves the trampoline at an initial height of 1.20 m
and reaches a maximum height of 4.80 m before falling back
down. What was the initial speed of the gymnast?

18. 6.3 Gravitational Potential Energy
1
2
W
Wgravity
mv f2
mg ho
1
2
2
mv o
mg ho h f
2
mvo
hf
vo
vo
1
2
2 9.80 m s 2 1.20 m 4.80 m
2 g ho h f
8.40 m s

19. 6.3 Gravitational Potential Energy
Wgravity
mgho
mgh f
DEFINITION OF GRAVITATIONAL POTENTIAL ENERGY
The gravitational potential energy PE is the energy that an
object of mass m has because of its position relative to the
surface of the earth.
PE
mgh
1 N m 1 joule J

20. 6.4 Conservative Versus Nonconservative Forces
THE WORK-ENERGY THEOREM
Wnc
KE
PE

21. 6.5 The Conservation of Mechanical Energy
Wnc
KE
Wnc
PE
KE f
KE f
KE o
PE f
Wnc
Ef
KE o
PE f
PE o
PE o
Eo
If the net work on an object by nonconservative forces
is zero, then its energy does not change:
Ef
Eo

22. 6.5 The Conservation of Mechanical Energy
THE PRINCIPLE OF CONSERVATION OF
MECHANICAL ENERGY
The total mechanical energy (E = KE + PE) of an object
remains constant as the object moves.

23. 6.5 The Conservation of Mechanical Energy

24. 6.5 The Conservation of Mechanical Energy
Example 8 A Daredevil Motorcyclist
A motorcyclist is trying to leap across the canyon by driving
horizontally off a cliff 38.0 m/s. Ignoring air resistance, find
the speed with which the cycle strikes the ground on the other
side.

25. 6.5 The Conservation of Mechanical Energy
Ef
mghf
ghf
1
2
Eo
2
f
mgho
v2
f
gho
mv
1
2
1
2
1
2
2
o
mv
2
vo

26. 6.5 The Conservation of Mechanical Energy
ghf
vf
vf
1
2
v2
f
gho
2 g ho h f
2
2 9.8 m s 35.0m
1
2
2
vo
2
vo
38.0 m s
2
46.2 m s

27. 6.6 Nonconservative Forces and the Work-Energy Theorem
THE WORK-ENERGY THEOREM
Wnc
Wnc
mghf
Ef
Eo
1
2
2
f
mv
mgho
1
2
2
o
mv

28. 6.6 Nonconservative Forces and the Work-Energy Theorem
Example 11 Fireworks
Assuming that the nonconservative force
generated by the burning propellant does
425 J of work, what is the final speed
of the rocket. Ignore air resistance.
Wnc
mgho
mghf
1
2
2
mvo
1
2
mv 2
f

29. 6.6 Nonconservative Forces and the Work-Energy Theorem
Wnc
mghf
Wnc
425 J
1
2
mgho
mg h f
1
2
mv
2
f
1
2
2
o
mv
mv2
f
0.20 kg 9.80 m s 2 29.0 m
0.20 kg v 2
f
vf
ho
1
2
61m s

30. 6.7 Power
DEFINITION OF AVERAGE POWER
Average power is the rate at which work is done, and it
is obtained by dividing the work by the time required to
perform the work.
P
Work
Time
joule s
W
t
watt (W)

31. 6.7 Power
P
Change in energy
Time
1 horsepower 550 foot pounds second 745.7 watts
P
Fv

32. 6.7 Power

33. 6.8 Other Forms of Energy and the Conservation of Energy
THE PRINCIPLE OF CONSERVATION OF ENERGY
Energy can neither be created not destroyed, but can
only be converted from one form to another.