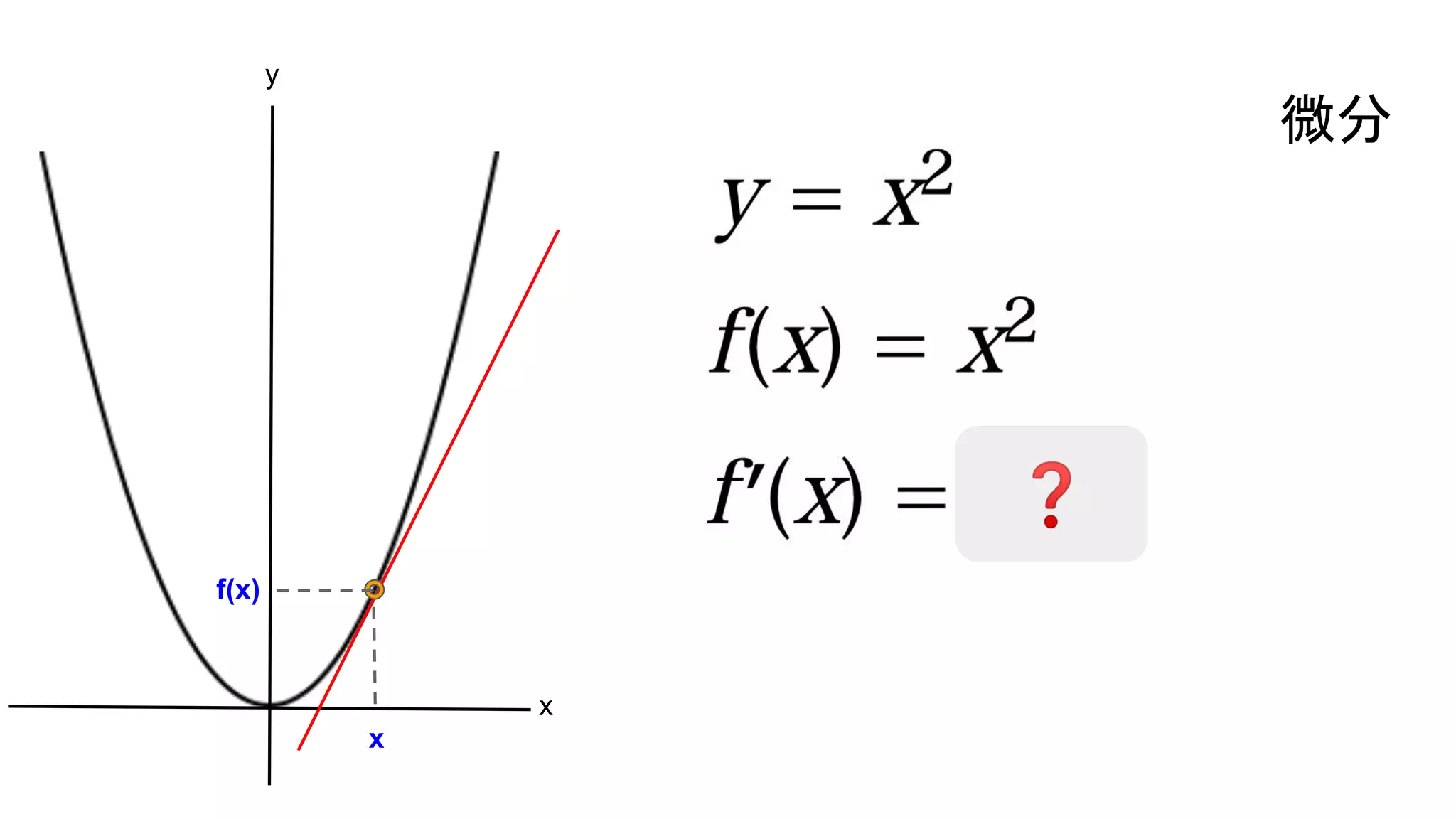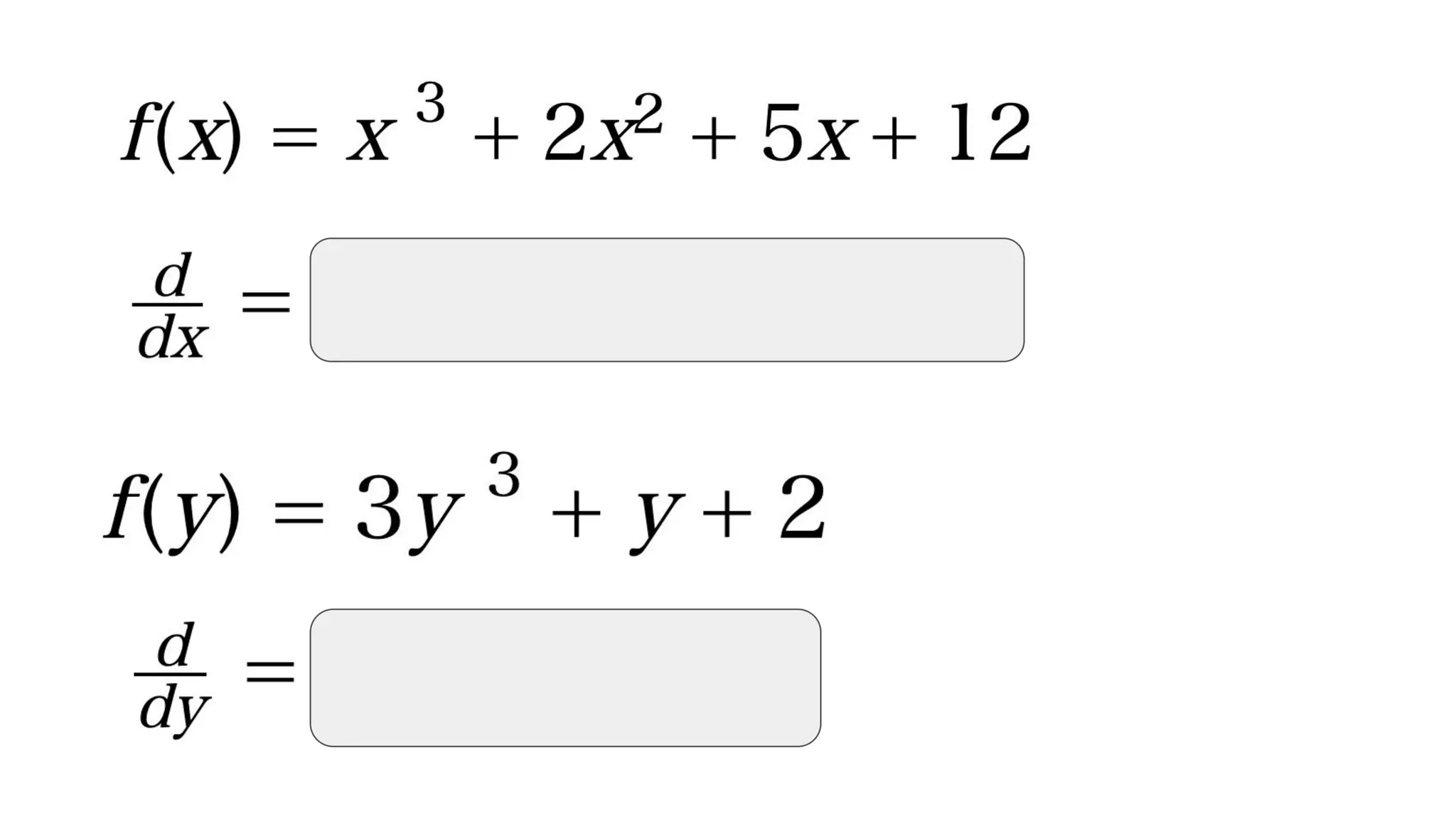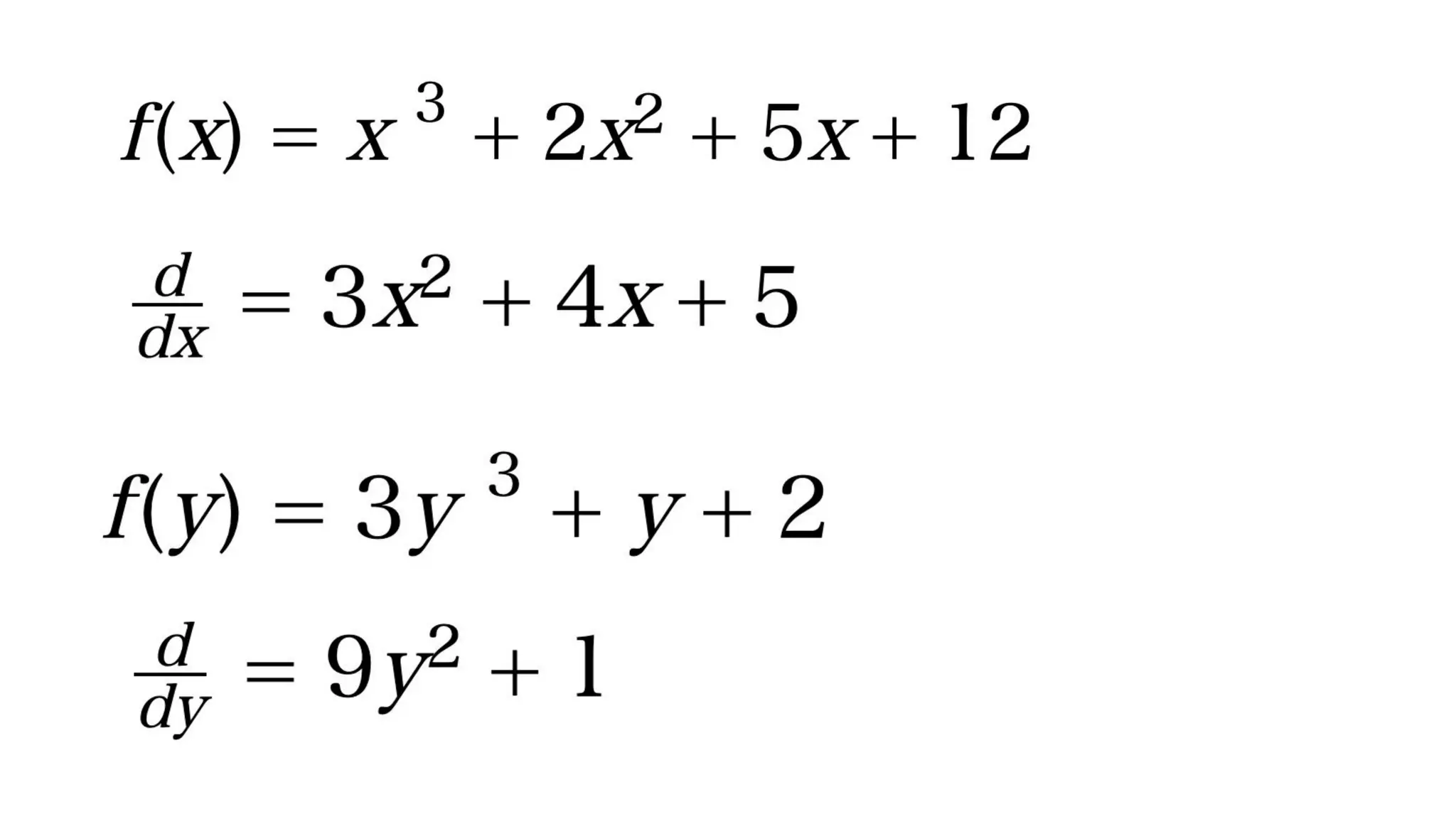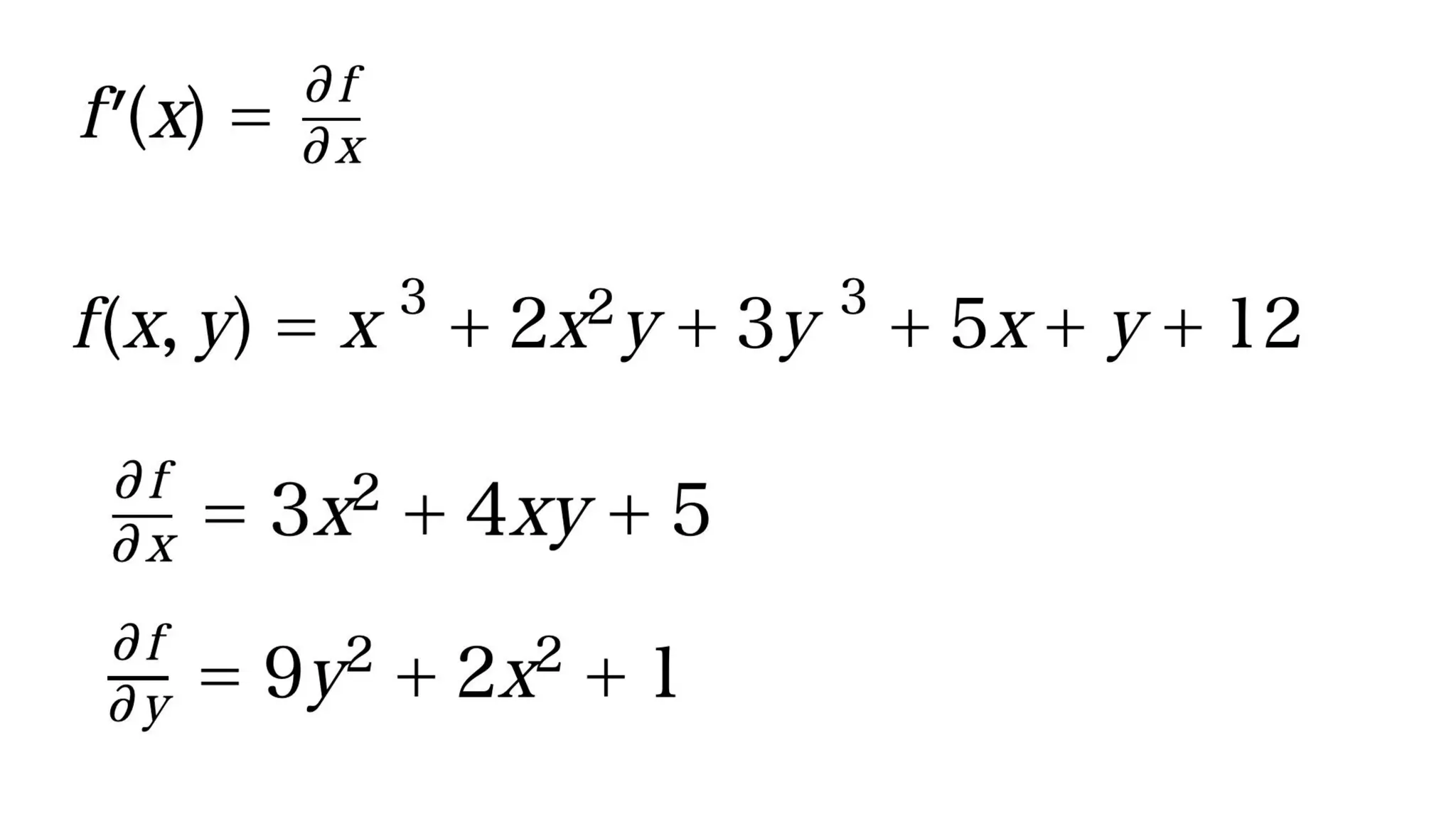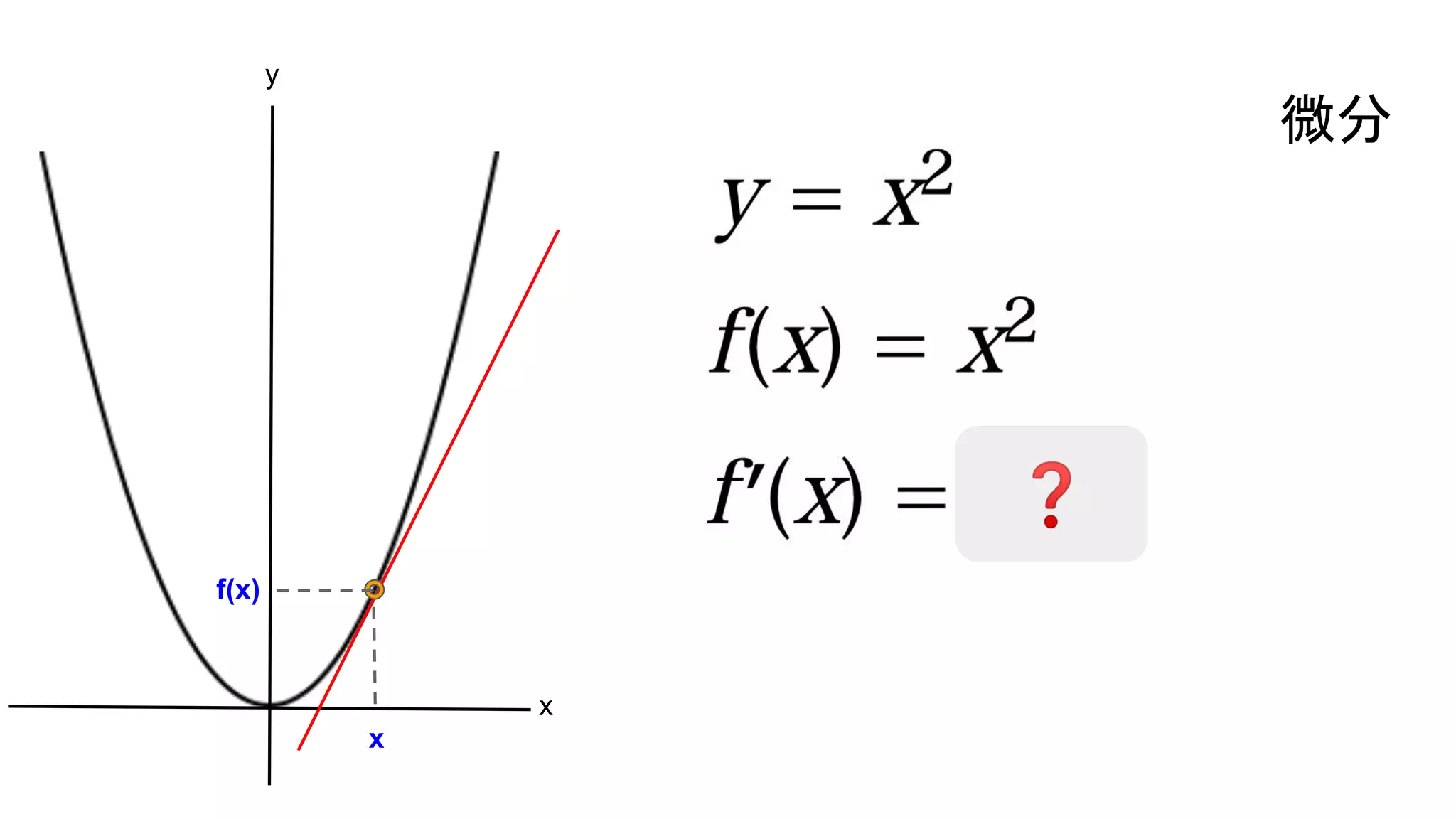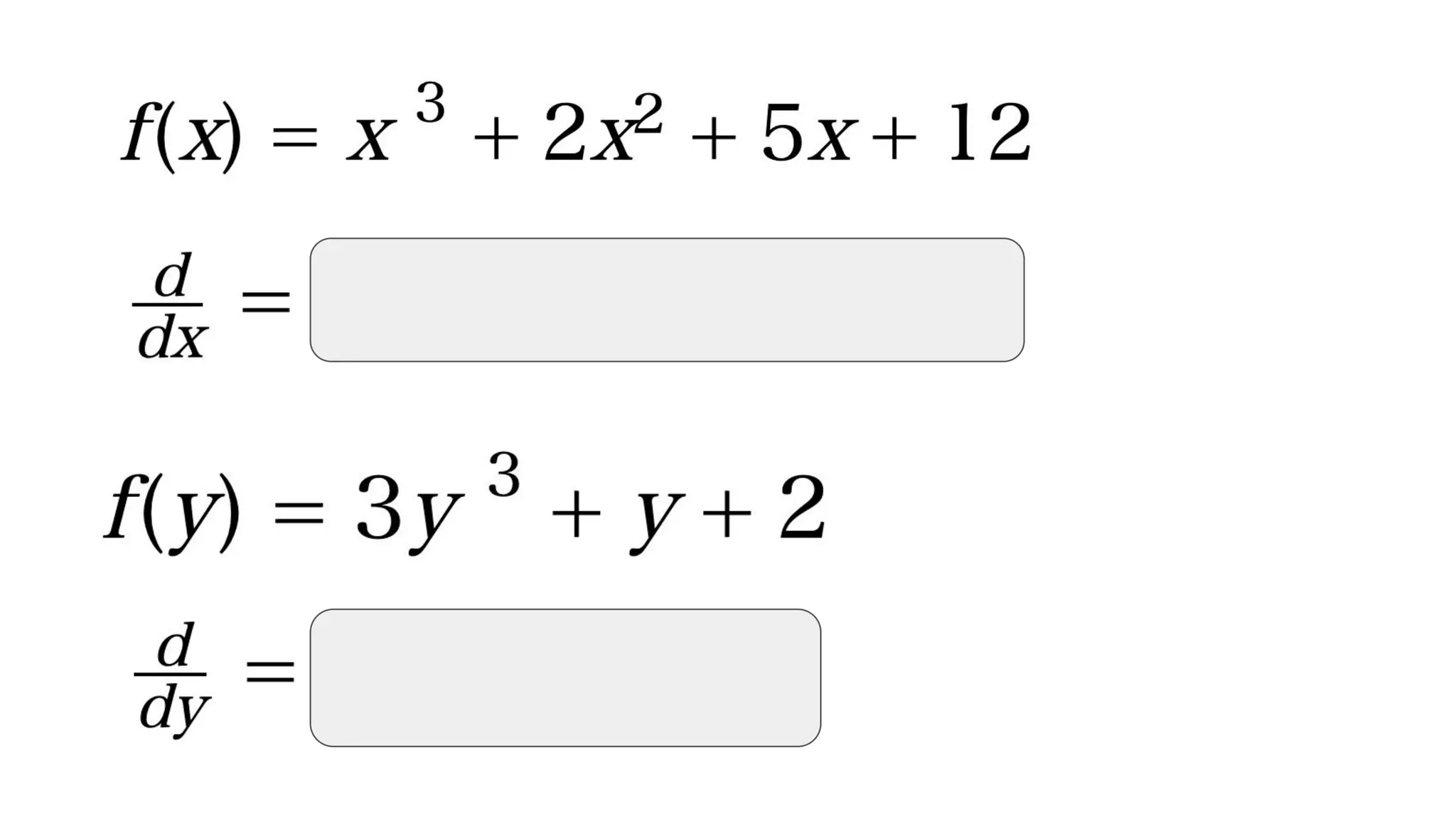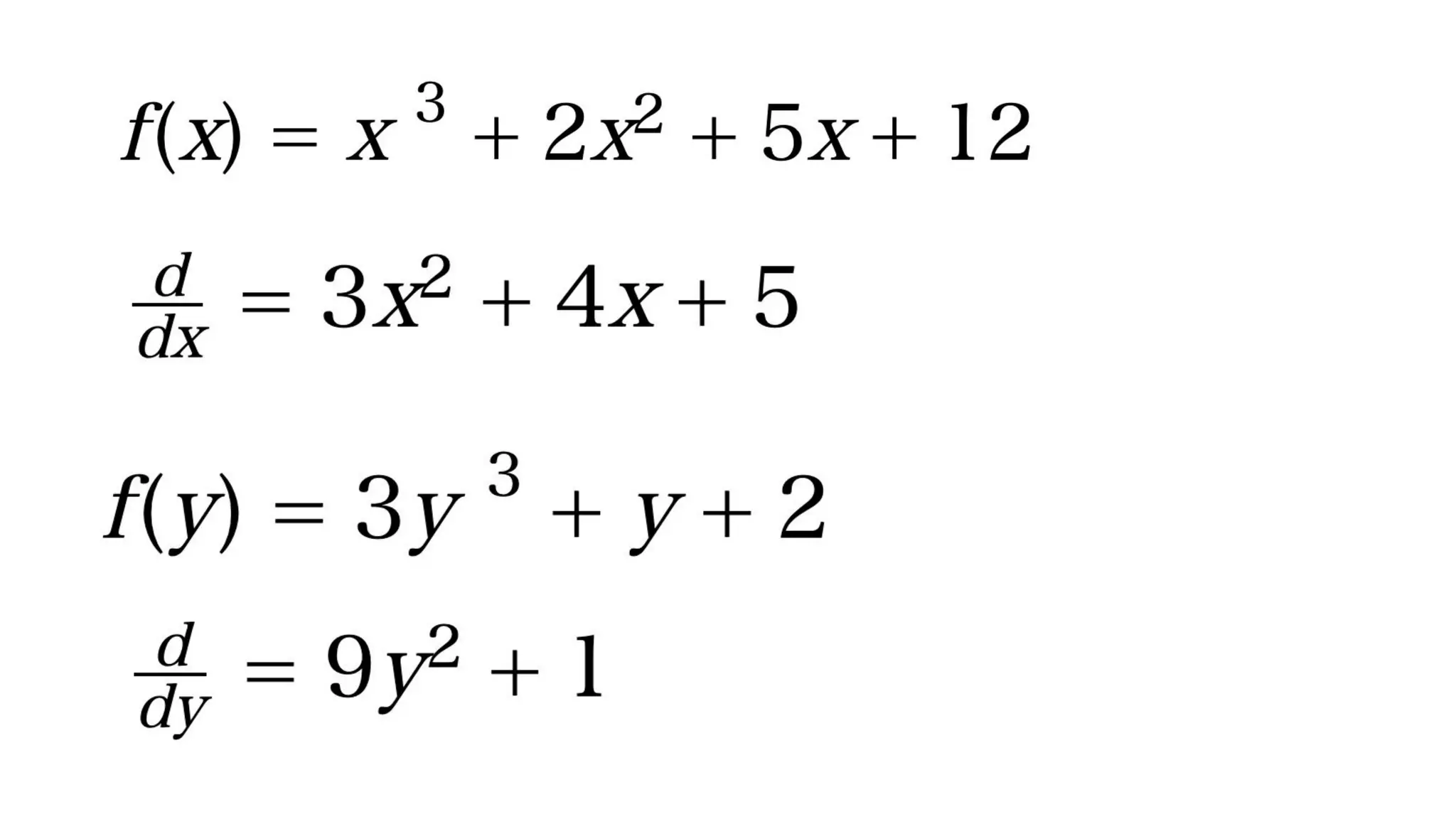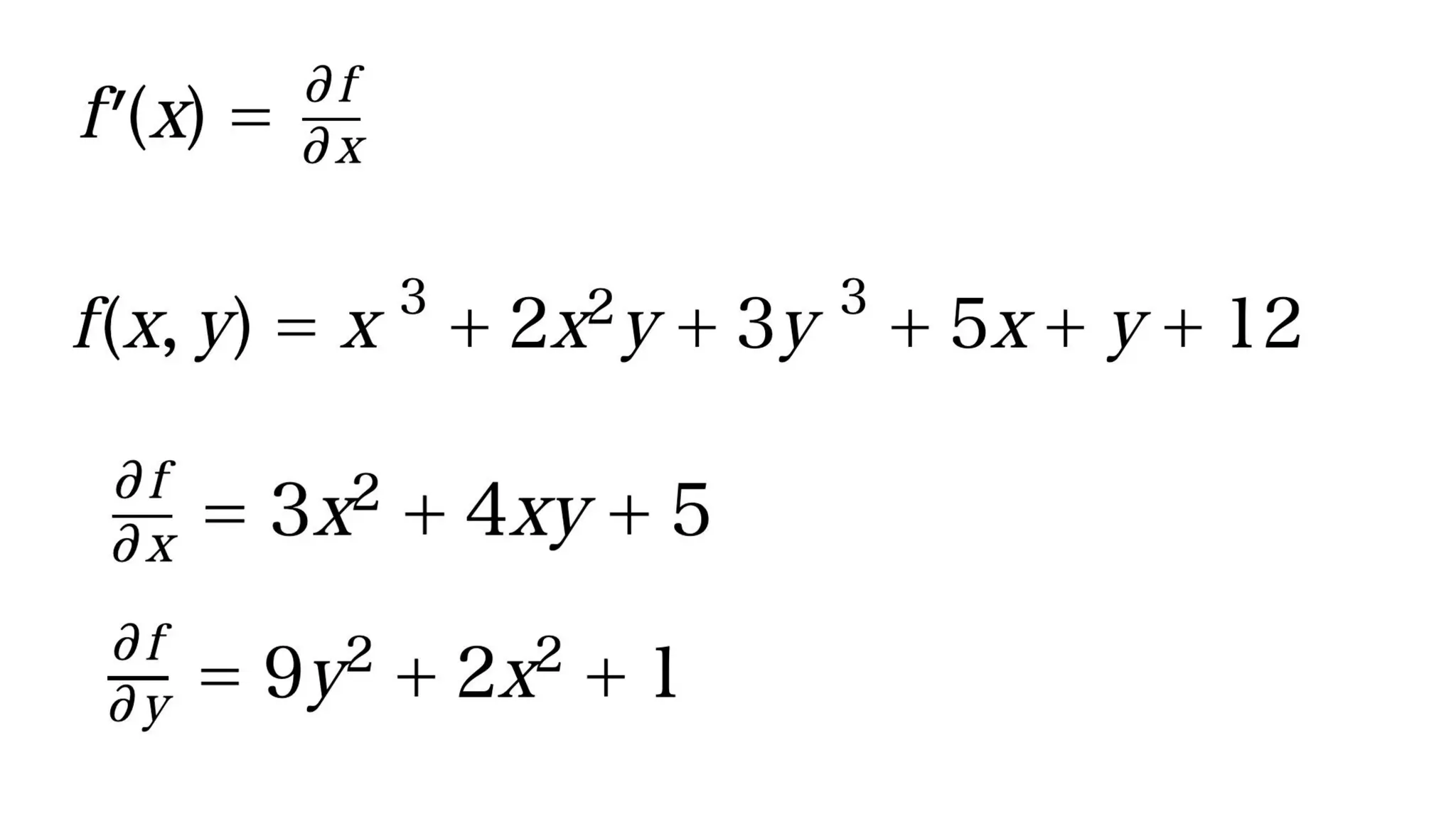More Related Content
PDF
PPTX
Magnitude ~ extend the Euler Characteristics via Möbius Inversion ~ PDF
PDF
PPTX
Operad and Recognition Principle PPTX
Introduction to Persistence Theory PPTX
PDF
What's hot
PPTX
Introduction to Topological Data Analysis PPTX
PDF
PPTX
PPTX
PPTX
PDF
PDF
PDF
PDF
PDF
imset による条件付き独立性の記述(文献紹介) PPTX
PDF
introductino to persistent homology and topological data analysis PDF
Introduction to Categorical Programming PDF
パターン認識と機械学習 §8.3.4 有向グラフとの関係 PPTX
PDF
PDF
PDF
Introduction to Categorical Programming (Revised) PDF
PRML輪講用資料10章(パターン認識と機械学習,近似推論法) More from Akihiro ITO
PDF
Bootleg_202303_越境してみたときのアウェイ感。.pdf PDF
PDF
202209_kintoneCafeNagoya_deepkintone.pdf PDF
20220810_JDLA合格者の会_CDLE_LT_06.pdf PDF
20220713_JP_Stripes#100-3 PDF
20200930 CDLE LT#2_COD_AkihiroITO PDF
PDF
2019_G検定対策_数学講座02_行列とベクトル PDF
2019_G検定対策_数学講座01_ディープラーニングでの基礎計算問題 PDF
20190301_SkillUpAI_AI導入スタートへのG検定活用 PDF
20181022 abeja cloudai_night_nico_airesourcedev PDF
20181016 ceatec2018 meti_session_nico_ito PDF
201807_AnnotationMeetUp_JetsonTX2での顔認識+Annotation用UIの実装 PDF
Jetson TX2での顔認識+Annotation用UIの実装 PDF
「G検定」を受けてみた。 2018/6/6 JSAI2018 PDF
JDLA Deep Learning for GENERAL 2017(所謂、G検定)はどんなだったか。 Recently uploaded
PDF
ふみこんで学ぶ世界遺産700<第2版>世界遺産検定準1級公式テキスト(2026年発売) PDF
プログラミング講座 【小学校高学年向け】Revision 6 2025/11/30 PPTX
Introduction to Japanese Language Learning.pptx PDF
横浜国立大学3年生に向けて研究室を紹介するスライド【2026年度研究室配属について】 PDF
高等専門学校卒業資格における準学士学位 (Associate Degre) の制度的展望 —国際的学位制度との比較から— PDF
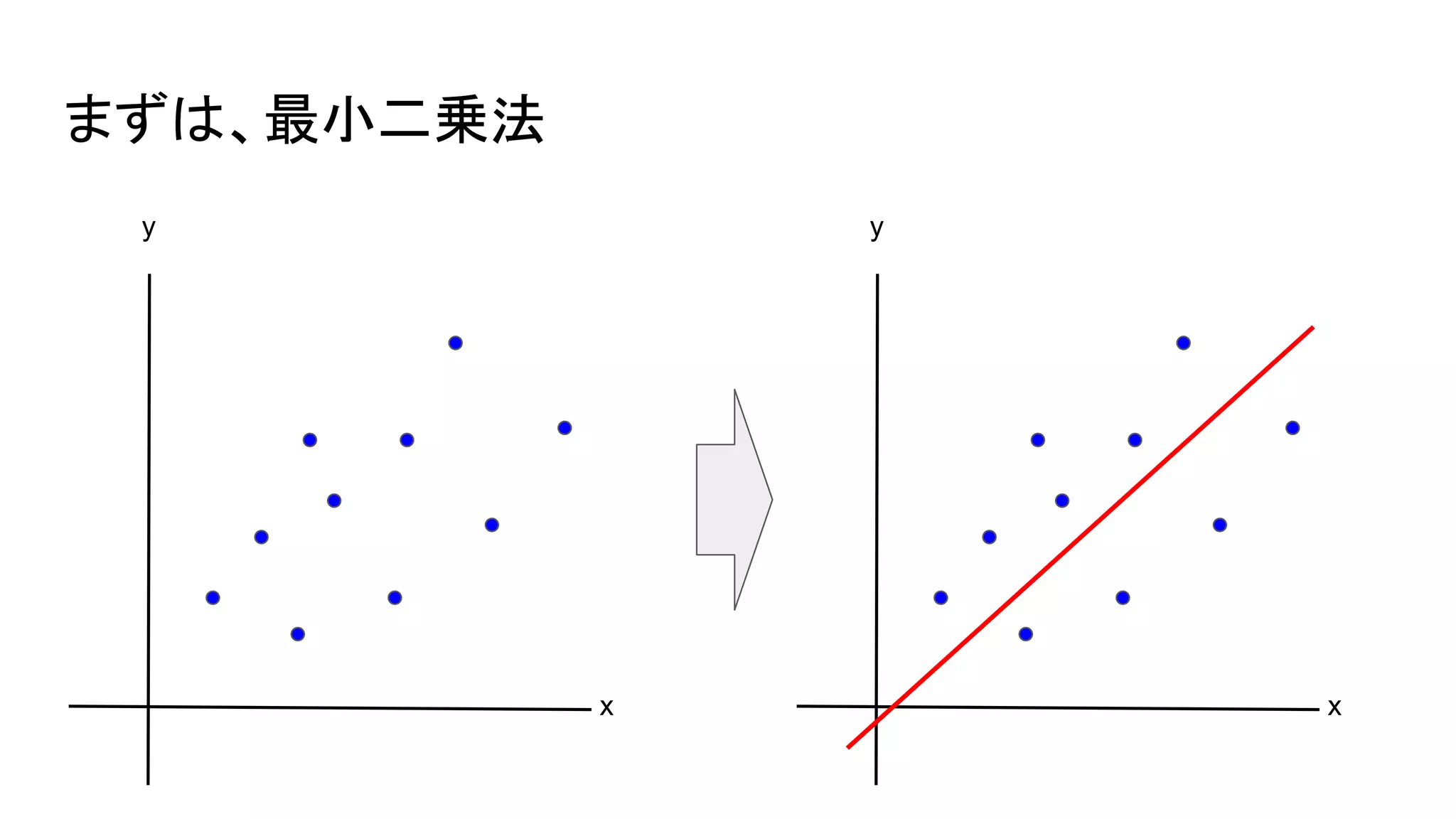
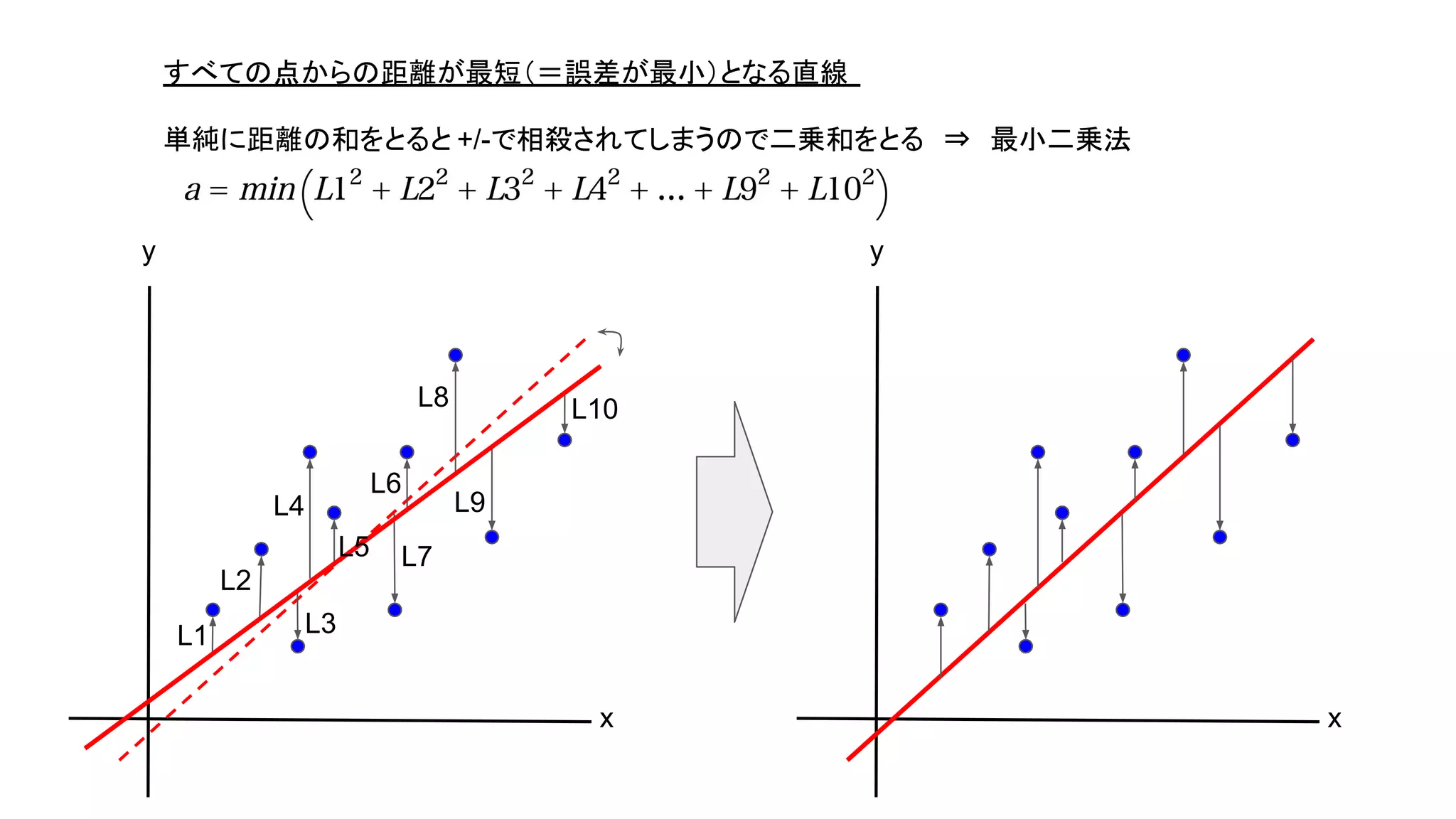
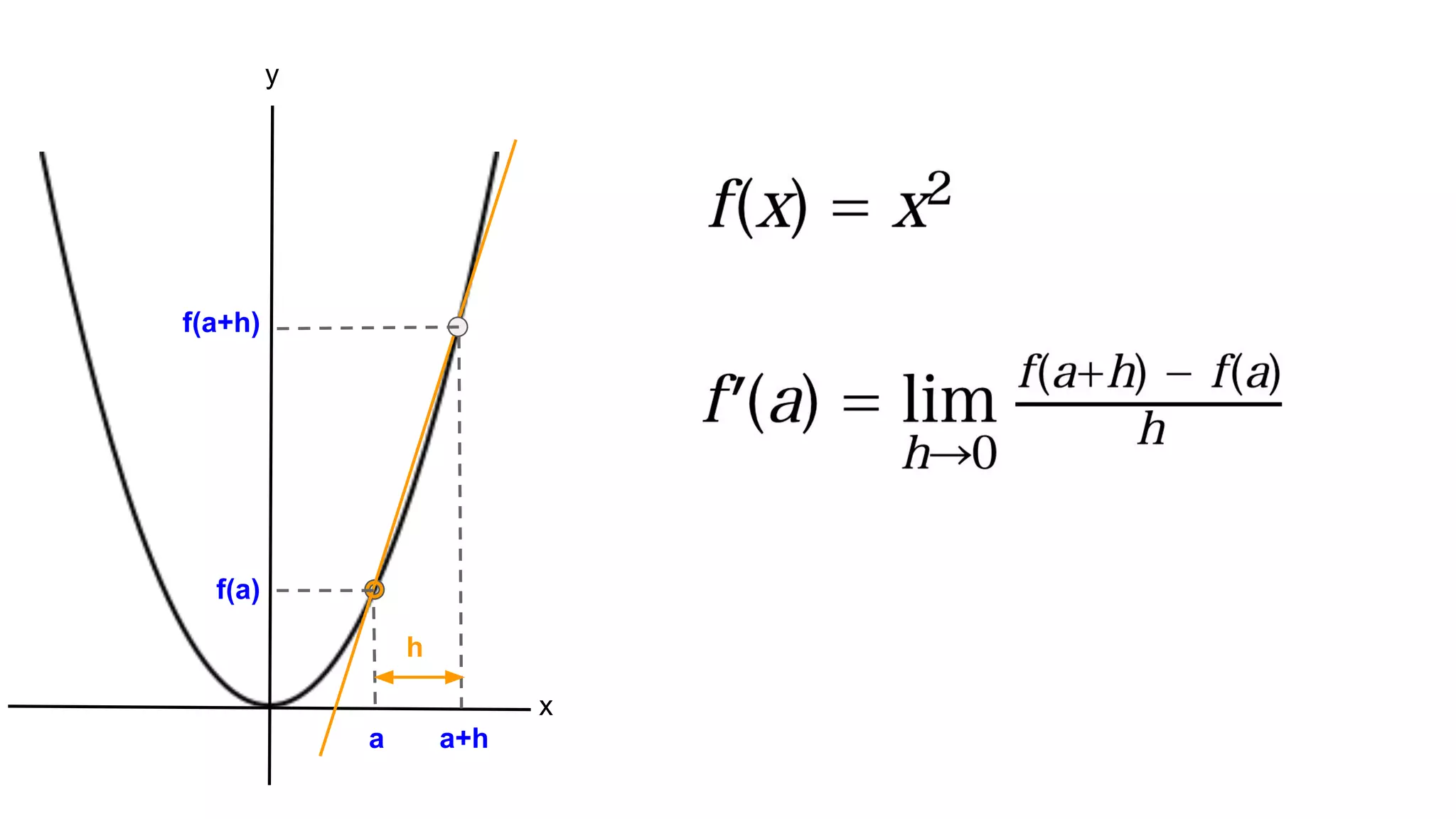
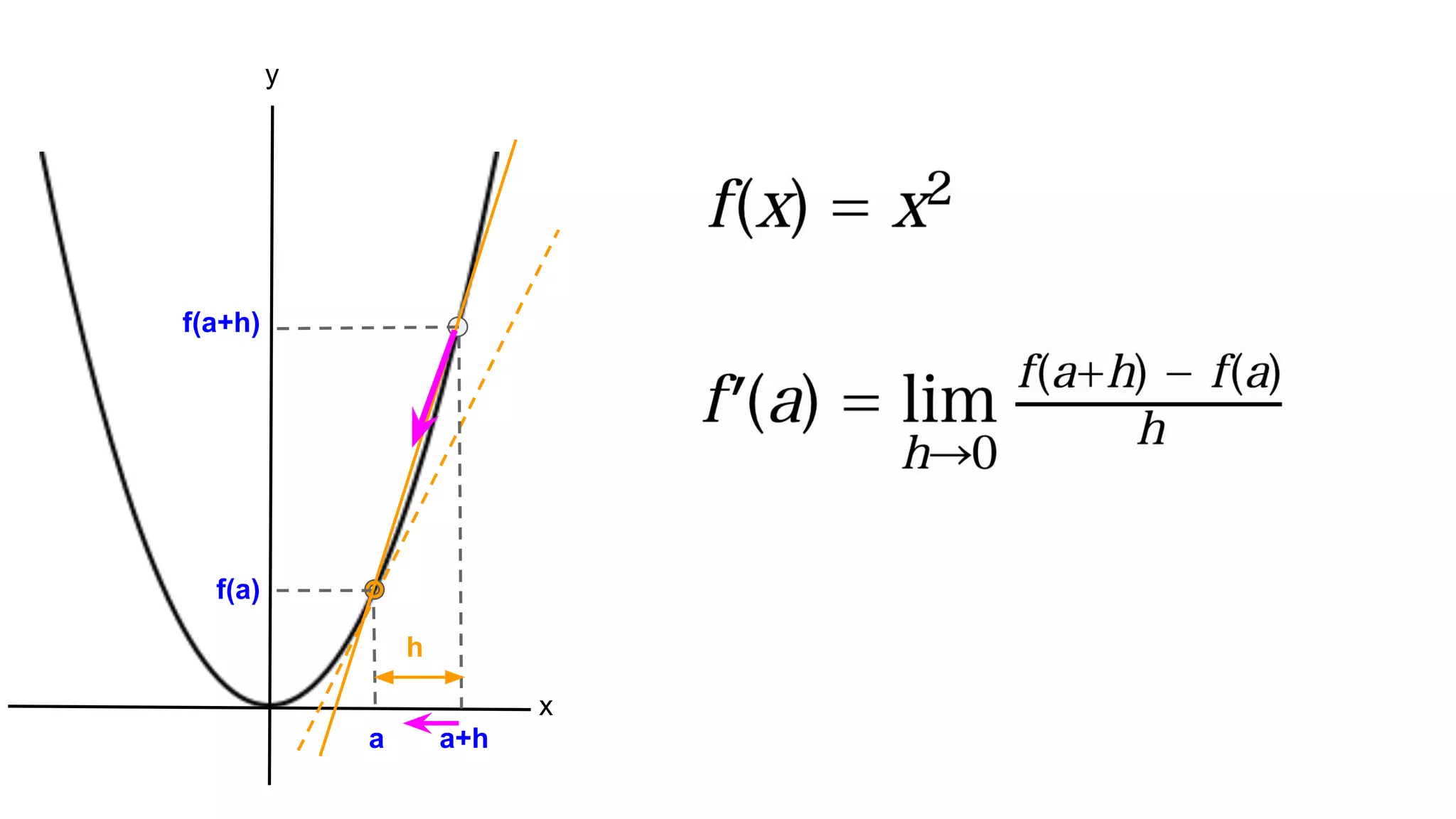
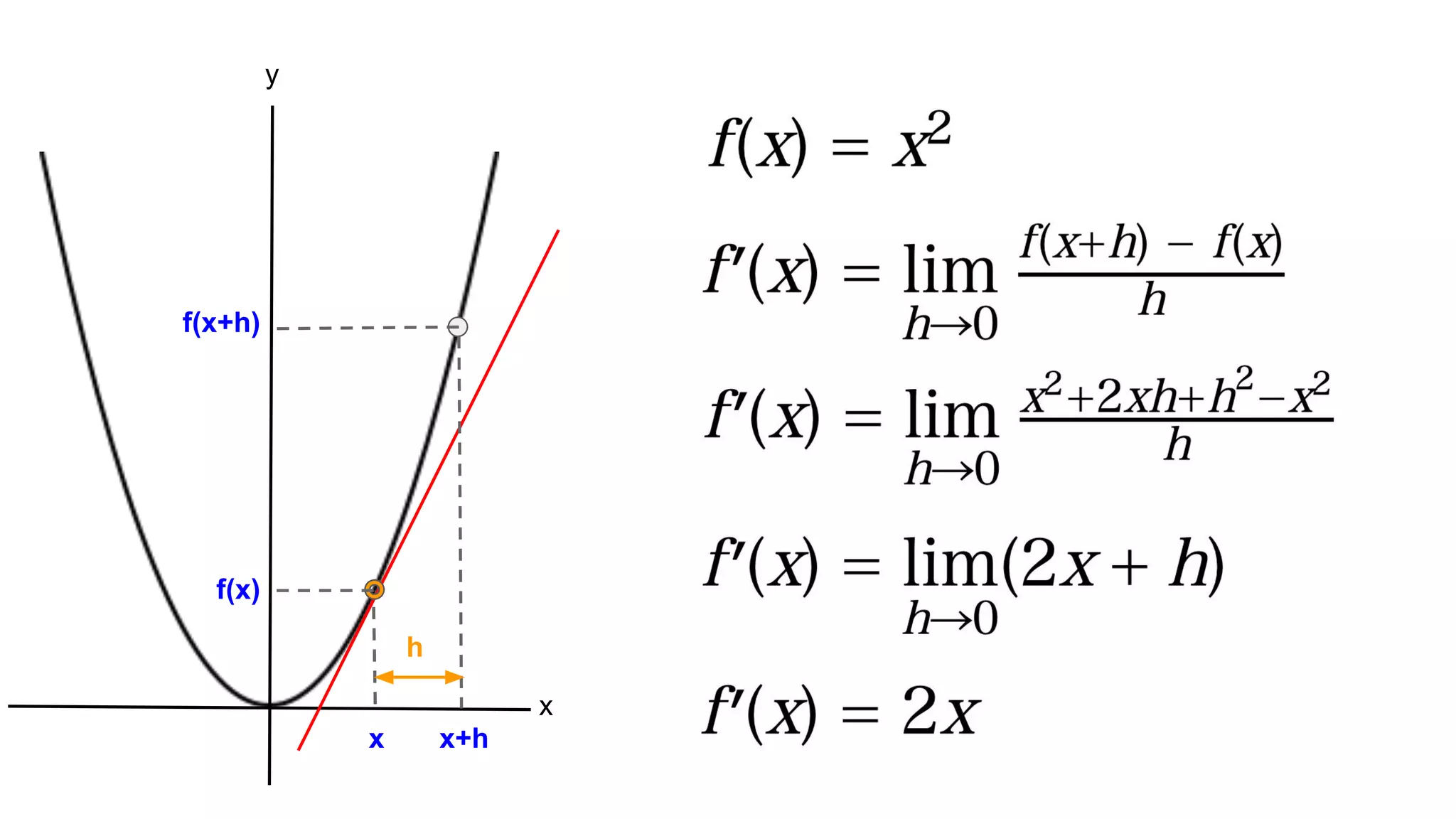
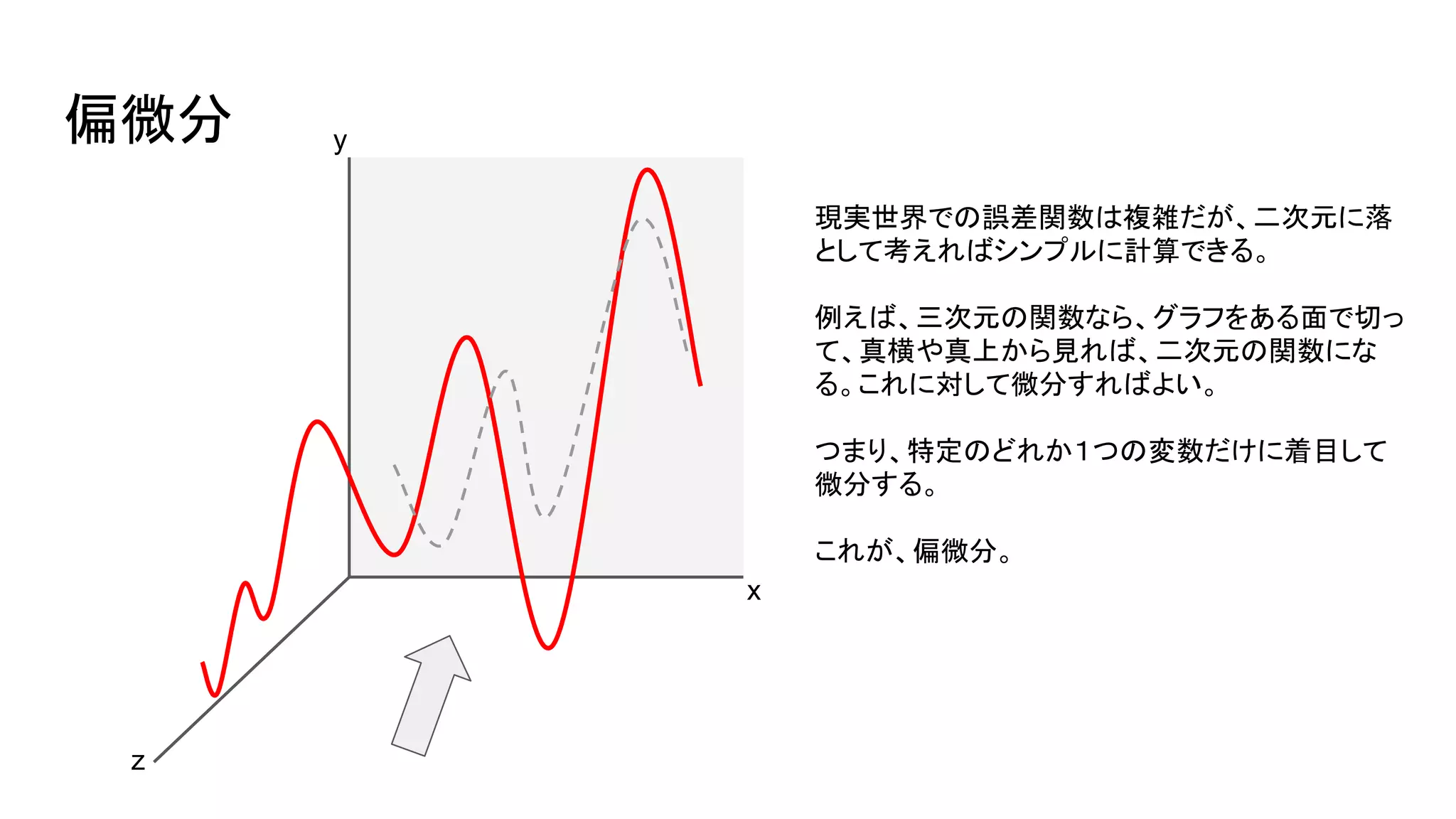
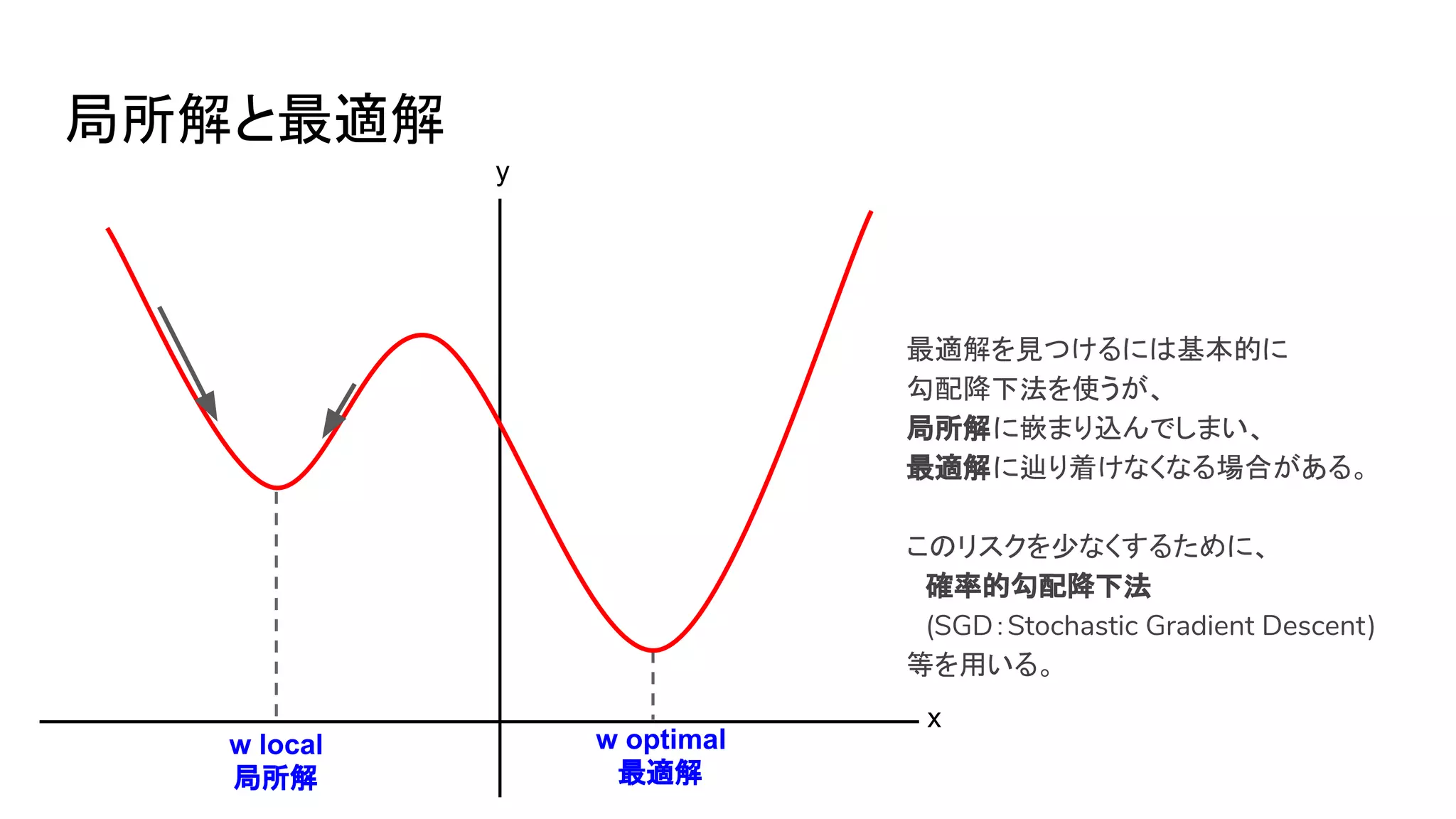
横浜国立大学3年生に向けて研究室を紹介する資料【2026年度研究室配属について】 2019_G検定対策_数学講座03_微分
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 10.
- 13.