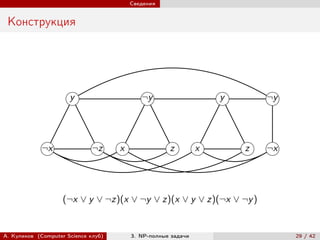
Лекция обрещает внимание на np-полные задачи в области информатики, включая задачи поиска, такие как пропозициональная выполнимость, задача о коммивояжере и задача о рюкзаке. Обсуждаются эффективные алгоритмы для решения определенных задач, способных работать за полиномиальное время, и графические задачи с экспоненциальным числом кандидатов. Лектор также объясняет, как задачи оптимизации могут быть переформулированы как задачи поиска без изменения их сложности.