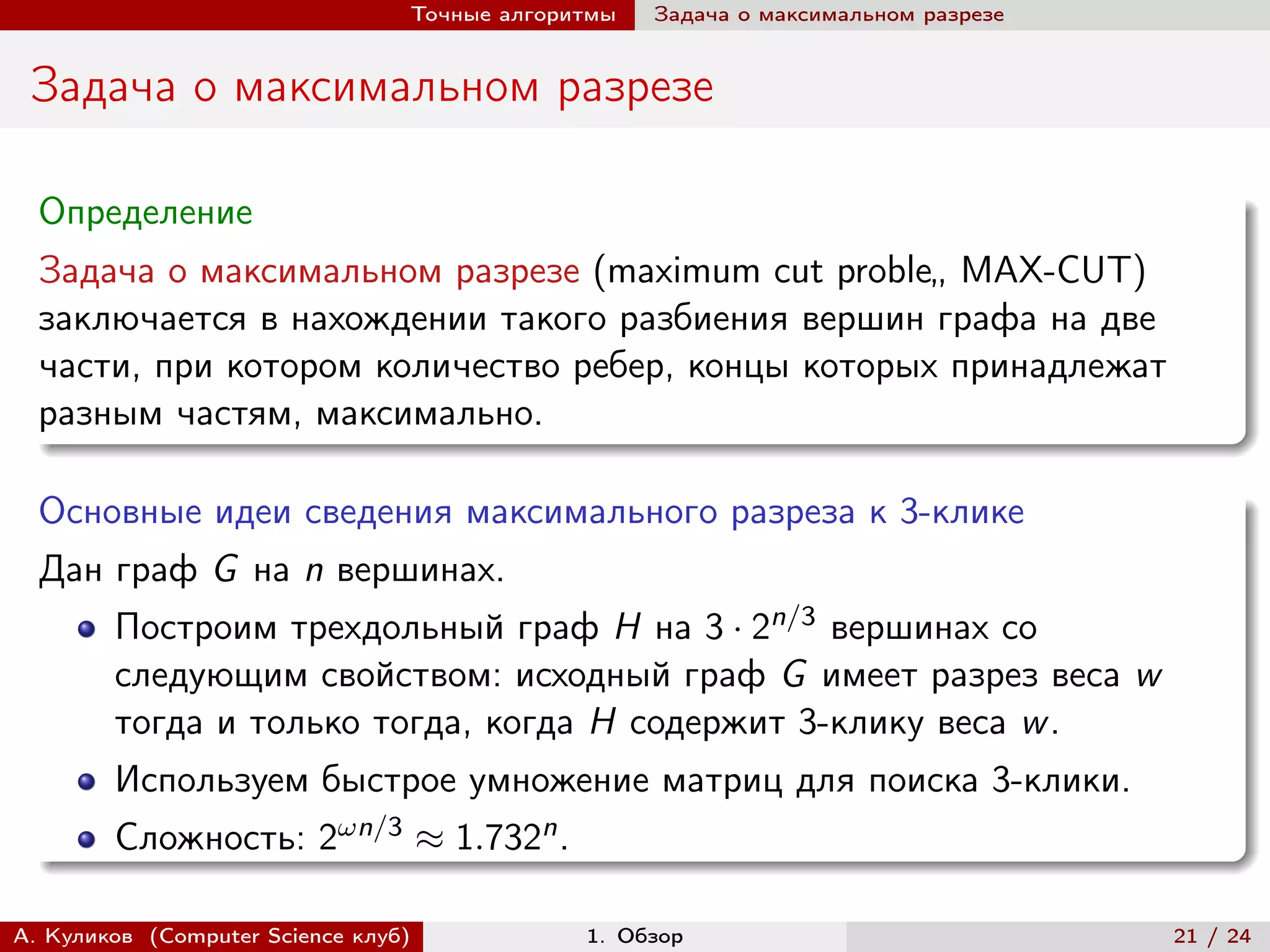
Лекция об алгоритмах для NP-трудных задач вводит понятия классов P и NP, а также обсуждает важность NP-полных задач. Основное внимание уделяется трудностям нахождения полиномиальных алгоритмов для этих задач, а также методам поиска решений для задач выполнимости. Лекция также рассматривает сравнение разных подходов к решению этих сложных задач.





























![Точные алгоритмы Задача о максимальном разрезе
Анализ алгоритма
Лемма
Алгоритм выдает правильный ответ за время O(n ), где ≈ 2.376 —
экспонента перемножения матриц (matrix multiplication exponent).
Доказательство
важное свойство матрицы смежности: Ak [i, j] есть количество
путей длины k из вершины i в вершину j в графе G (легко
доказать по индукции)
А. Куликов (Computer Science клуб) 1. Обзор 20 / 24](https://image.slidesharecdn.com/20090913algorithmsfornphardproblemskulikovlecture01-100811010042-phpapp02/75/20090913-algorithmsfornphardproblems-kulikov_lecture01-56-2048.jpg)
![Точные алгоритмы Задача о максимальном разрезе
Анализ алгоритма
Лемма
Алгоритм выдает правильный ответ за время O(n ), где ≈ 2.376 —
экспонента перемножения матриц (matrix multiplication exponent).
Доказательство
важное свойство матрицы смежности: Ak [i, j] есть количество
путей длины k из вершины i в вершину j в графе G (легко
доказать по индукции)
3-клика — это путь длины 3 из вершины в саму себя
А. Куликов (Computer Science клуб) 1. Обзор 20 / 24](https://image.slidesharecdn.com/20090913algorithmsfornphardproblemskulikovlecture01-100811010042-phpapp02/75/20090913-algorithmsfornphardproblems-kulikov_lecture01-57-2048.jpg)
![Точные алгоритмы Задача о максимальном разрезе
Анализ алгоритма
Лемма
Алгоритм выдает правильный ответ за время O(n ), где ≈ 2.376 —
экспонента перемножения матриц (matrix multiplication exponent).
Доказательство
важное свойство матрицы смежности: Ak [i, j] есть количество
путей длины k из вершины i в вершину j в графе G (легко
доказать по индукции)
3-клика — это путь длины 3 из вершины в саму себя
для вычисления A3 требуется два умножения матриц
А. Куликов (Computer Science клуб) 1. Обзор 20 / 24](https://image.slidesharecdn.com/20090913algorithmsfornphardproblemskulikovlecture01-100811010042-phpapp02/75/20090913-algorithmsfornphardproblems-kulikov_lecture01-58-2048.jpg)