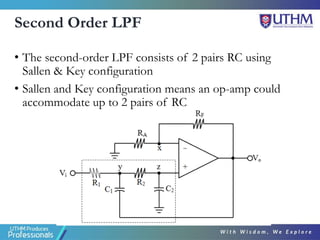
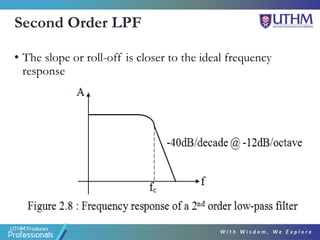
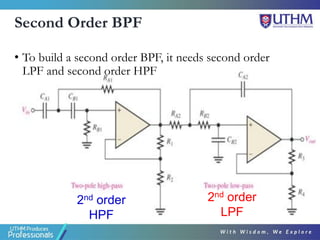
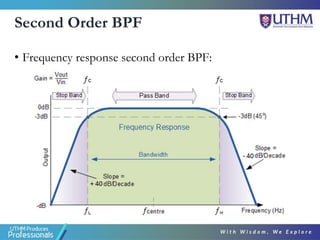
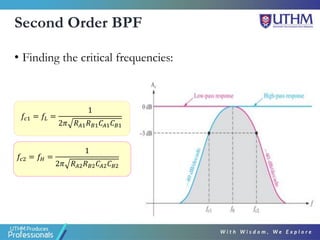
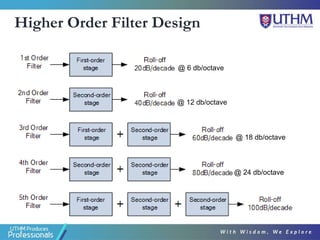
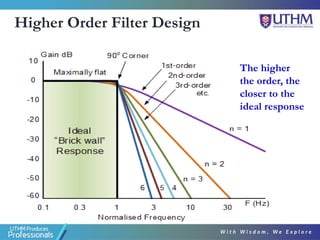
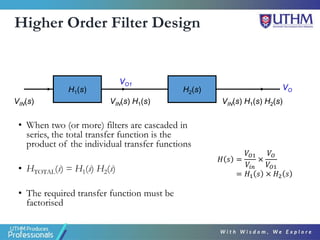
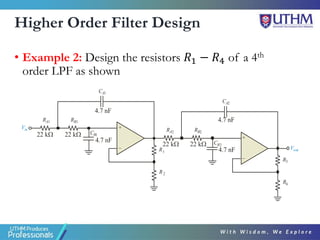
This document discusses the design of second order active filters including low pass, high pass, and band pass filters. It describes how to design these filters using Sallen-Key configurations with op-amps. Higher order filters can be designed by cascading multiple lower order filter sections. The document provides examples of designing second order high pass and fourth order low pass filters by calculating component values based on desired cut-off frequencies and Butterworth polynomials.