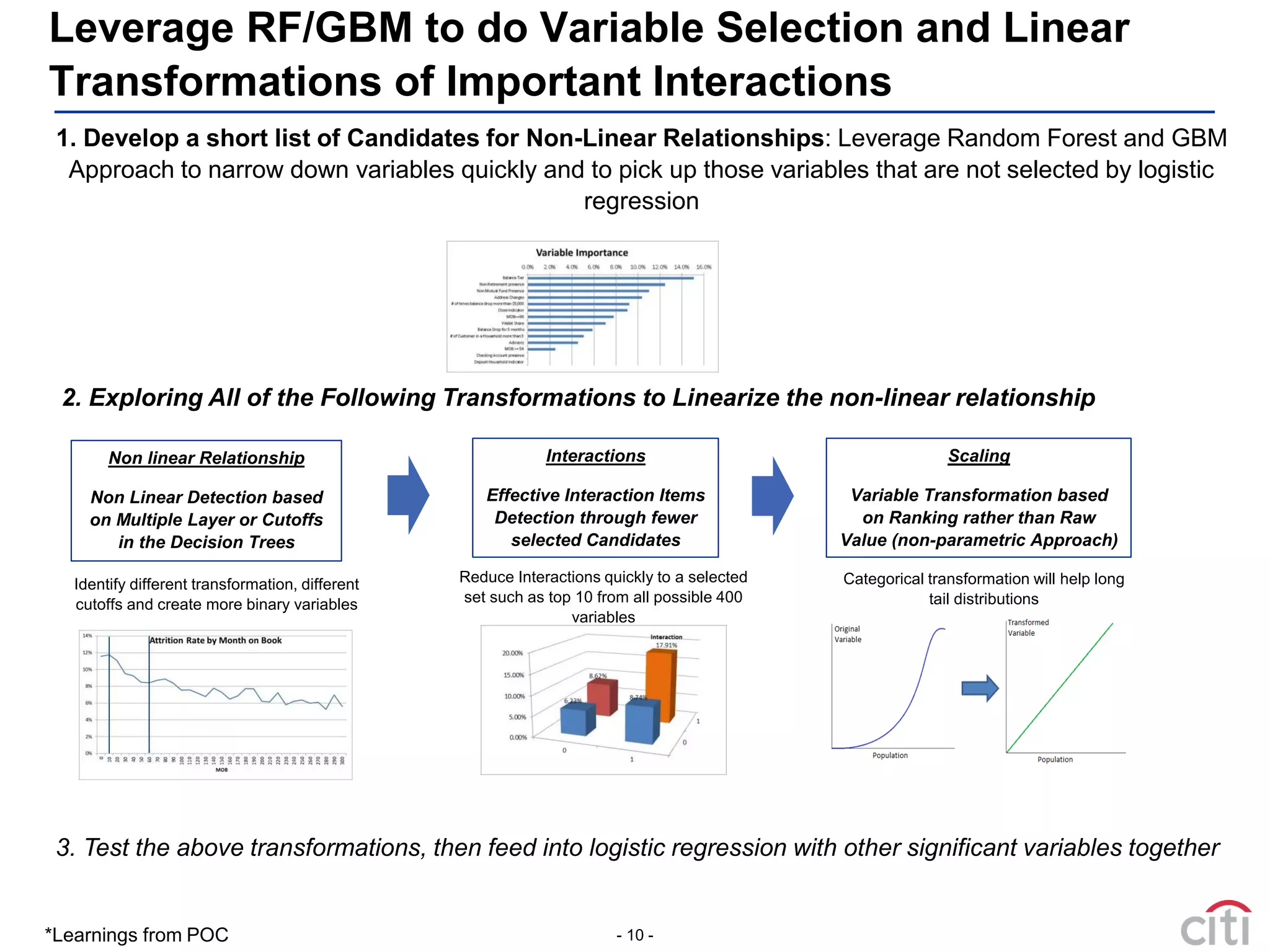
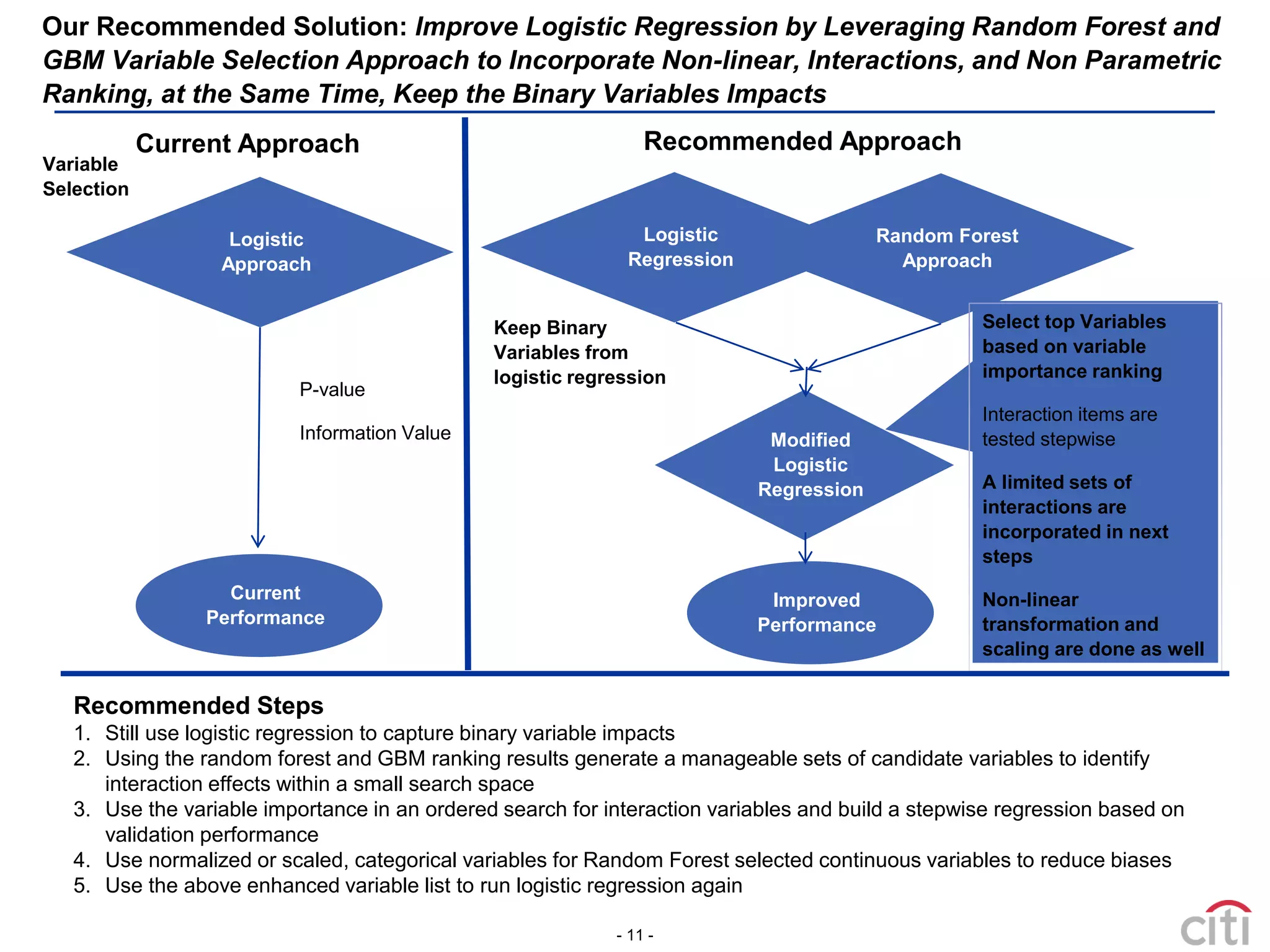
This document proposes a modified logistic regression approach that leverages random forest and gradient boosted machines (GBM) to enhance variable selection. It begins by discussing how different variable selection methods can generate different predictive drivers. It then reviews literature showing random forest often outperforms logistic regression and is well-suited for credit scoring. The document explains how algorithm selection is intertwined with variable selection and variable transformations. It recommends using random forest and GBM to narrow variables, detect non-linear relationships and interactions, and transform variables before incorporating them into a modified logistic regression model. This hybrid approach aims to incorporate benefits from both ensemble methods and logistic regression.

1. A Modified Logistic Regression Approach Enhanced by
New Interactions and Scaling Detections through
Random Forest and GBM
Yulin Ning, Senior Director
Next Gen Analytics
Global Analytics Platform and Capabilities
Citi Global Consumer Bank
Predictive Analytics World, New York
Oct 30th, 2017
Presenter’s View Only – does not reflect Citigroup’s View

2. - 1 -
Who Are We and What Our Strategy Is
Infrastructure / Data
Processes
Platforms and CapabilitiesCiti Global Consumer
Priorities
POC Management
Framework
Ongoing Industry
Research
Talent / Data
Scientist Disciplines
Capabilities
Development / POCs
Innovative Culture
Next Generation
Analytics Strategy
Customer
Centricity
Global
Digital Bank

3. - 2 -
Today’s Topic
A Modified Logistic Regression Approach Enhanced by New
Interactions and Scaling Detections through Random Forest and
GBM - A practical adoption of machine learning into predictive analytic discipline
Problem statement: algorithm selection intertwines with variable selection methods
Literature review
Key components of predictive analytics
Algorithm selection Intertwining with variable selection
Use Random Forest (RF) and GBM to enhance variable selection
A modified logistic regression approach to incorporate benefit from Random Forest and GBM

4. - 3 -
Problem Statement: Different Variable Selection Methods
Generated Different Drivers During our POC Work
 A variety of methods were explored by our 3 MAs (Liana,Jonathan, and Jason) to do the initial variables/drivers
selections for one of our POC
 Stepwise variable selection and information value method based on logistic regression
 Variable importance based on Random Forest and GBM
 Different methods generate different results, reflecting the needs to re-fining the modeling options to ensure scaled,
un-biased, and conditional variable importance
*Learnings from POC
Binary Indicator Variables
(a total of 17 Variables)
Category variables
Continuous variables
(7 Variables are exactly
the same, 22 similar type,
but not exactly the same)
Continuous Balance
Variables(5 Variables)
 15 Closed Account Indicators
 6 Other Indicators
 16 are count related variables
 3 Balance related fields
• Only 60% Overlap for similar type of
variables
• Only 14% variable are exactly the same
• Binary variables are skewed to the left and
continuous variables are skewed to the
right
 10 Balance variables
 13 count related fields
 4 Indicators
 3 Categories
Logistic
Random
Forest

5. - 4 -
Our Experience Triggered us to Do: Literature Review on
Variable Selection Methods Comparisons
Although there are a lot of different options for algorithms, the good news is that only a few handful
algorithms have been consistently out-performing.
1. Random Forest is found to perform better than logistic regression in literature
Why and how to use random forest variable importance measures, Carolin Strobl (LMU M¨unchen) and Achim Zeileis (WU Wien), 2008, Dortmund
Elements of Optimal Predictive Modeling Success in Data Science: An Analysis of Survey Data for the ‘Give Me Some Credit’ Competition Hosted on Kaggle, Dhruv
Sharma, March 2, 2013
Random forests have been found to outperform standard logistic regression models by 5-7% and well suited for credit scoring out of the box due to their ability to deal with
corrected variables which confound modeling process using regression methods (Sharma, 2009, Sharma, 2011)
2. Kaggle Competition Results also indicate random forest is a favorite approach by data
scientists a few years earlier
3. GBM is a relative new phenomena
4. Deep learning gains popularity for unstructured data handling recently

6. Key Components of Predictive Analytics
Feature Generations
• Event
• Interactions
• Non-linear Transformation
• Peer Statistics
• ……
Algorithms
• Decision Trees
• Logistic Regression
• Support Vector Machine
• Random Forest
• GBM
• Deep Learning
• AI
• ……
Computing Proficiency
Scalable parallel processing
In-memory pull (Spark)
Iterations for converging
Variable Selection
Adaptive Feedback Loop
Adaptive learning
Real Time Delivery
Real time business benefit
Profile Data
Transaction Data
Event
Contextual
Interaction
Digital
Social
Value of Data Value of Algorithms
Driver Analysis
Value of Time

7. - 6 -
Algorithm Selection Intertwining with Variable Selection
and Fundamental Algorithm Assumptions
 Algorithm selection impacts final variable selected and assumptions made
Variable
Selection
Model Fitting
Model
Validations
Assumptions
Algorithm
Selection
Key Points
 Distribution
 Categorical
 Non-linear relationship
 Type of relationship

8. - 7 -
Fundamental Understandings: Random Forest’s
Strengths and Weaknesses versus Logistic Regression
Logistic Regression Random Forest
Strength • Conventional methods and easy to
execute
• Un-biased estimate for binary variable
• The most powerful aspect about random forests is
variable importance ranking which estimates the
predictive value of variables by scrambling the variable
and seeing by how much the model performance drops.
• Variable importance captured non linear as well as
interaction impacts among variables
• A probability is associated with many different trees,
variable selection will be more stable
• Variable importance reflects both the significant level as
well as the weight of the coefficient
Weakness • Too much focus on the significant level,
less focus on the weight of the
coefficients
• It is up to modeler to detect and
incorporate the non-linear transformation
as well as interactions
• Default option is biased towards continuous variables,
less favor of categorical and binary variables
• Unbiased solution is very complex and computationally
intensive (cforest package)
Ensemble Approach is Needed
• Incorporate binary variable impact
• Incorporate non linear relationship
• Incorporate interactions
• Scaling continuous variables from Random Forest approach to reduce biases
 No one method is perfect, ensemble approach tends to perform better
 Un-biased, conditional, and scaling in Random Forest is very computationally intensive and is less practical
 A simplified modified logistic regression is more appropriate by using Random Forest as a variable selection and non-
linear transformation tool

9. - 8 -
Fundamental Understandings: Random Forest as
Compared with GBM
Key Observations:
 Random sampling with replacement
 Multiple datasets, same algorithms or
parameter controls
 Random variable columns and random row
selections (un-biased)
 Variable importance is derived from dropping
the variable, a backward calculation
……
Random with replacement Independent sampling
Average of Predictions
……
Random sampling from residual
Additive of Predictions
Key Observations:
 Random sampling without replacement
 Sequential residual datasets
 Weak leaners
 Same independent variables, different models
 Additive of predictions

10. - 9 -
Fundamental Understandings: GBM’s Strengths and
Weaknesses versus Random Forest
Random Forest GBM
Common • Both are ensemble learning methods and predict from individual trees. They differ in the way the trees
are built - order and the way the results are combined.
• No scaling of inputs, so you do not need to do careful features normalization, can learn higher order
interaction quickly, scalable for computing. Random Forest and GBM tree based machine learning
approaches intrinsically enact their feature selections.
• Random Forest trains each tree
independently. This randomness helps
reduce biases and less likely to overfit.
• Fewer parameters to tune
• GBM build trees one at a time, where each new tree
helps to correct errors made by previously trained tree.
With each tree added
• More parameters to tune, such as number of trees, depth
of trees and learning rate, and the each tree built is
generally shallow.
Data Drawn • Random with replacement
• Same algorithm, different samples
• Average
• Random without replacement
• Residual
• Additive prediction
Trade-offs • Low Bias + High Variance • High Bias + Low Variance
Strength • Easier to tune
• Un-biased estimate for binary variable
• A well-tuned model out-perform RF method
• Gradient boosting does a better job of handling
multicollinearity than RF
• GBM have tendency on concentrating on a few variables
Weakness • Do not do well with time
• Some times misinterpreted
• Easy to over fit
• More parameters to tune
• Take longer to train because of sequential nature

11. - 10 -
Leverage RF/GBM to do Variable Selection and Linear
Transformations of Important Interactions
Reduce Interactions quickly to a selected
set such as top 10 from all possible 400
variables
1. Develop a short list of Candidates for Non-Linear Relationships: Leverage Random Forest and GBM
Approach to narrow down variables quickly and to pick up those variables that are not selected by logistic
regression
Non linear Relationship
Non Linear Detection based
on Multiple Layer or Cutoffs
in the Decision Trees
Interactions
Effective Interaction Items
Detection through fewer
selected Candidates
Scaling
Variable Transformation based
on Ranking rather than Raw
Value (non-parametric Approach)
Categorical transformation will help long
tail distributions
Identify different transformation, different
cutoffs and create more binary variables
2. Exploring All of the Following Transformations to Linearize the non-linear relationship
3. Test the above transformations, then feed into logistic regression with other significant variables together
*Learnings from POC

12. - 11 -
Our Recommended Solution: Improve Logistic Regression by Leveraging Random Forest and
GBM Variable Selection Approach to Incorporate Non-linear, Interactions, and Non Parametric
Ranking, at the Same Time, Keep the Binary Variables Impacts
Recommended Approach
Logistic
Approach
Variable
Selection
Random Forest
Approach
Logistic
Regression
Modified
Logistic
Regression
Current Approach
Select top Variables
based on variable
importance ranking
Interaction items are
tested stepwise
A limited sets of
interactions are
incorporated in next
steps
Non-linear
transformation and
scaling are done as well
Keep Binary
Variables from
logistic regression
Improved
Performance
P-value
Information Value
Current
Performance
Recommended Steps
1. Still use logistic regression to capture binary variable impacts
2. Using the random forest and GBM ranking results generate a manageable sets of candidate variables to identify
interaction effects within a small search space
3. Use the variable importance in an ordered search for interaction variables and build a stepwise regression based on
validation performance
4. Use normalized or scaled, categorical variables for Random Forest selected continuous variables to reduce biases
5. Use the above enhanced variable list to run logistic regression again

13. - 12 -
 Benefit from Recommended Approach: An 0-10% Lift is Observed if we leverage
Random Forest for Non-linear relationship and Variables Interaction Detection
Benefit from Recommended Approach: An 0-10% Lift is
Observed

14. - 13 -
Conclusions
 Although there are a lot of different options for algorithms, the good news is that only a
few handful algorithms have been consistently out-performing. We did not need to start
from scratch. Although there are many different ways of coding, R, Java, Python, the
underlying algorithm are mostly similar. A lot of differences happened on the iteration
process, data re-engineering, and feature creations.
 Model variable selection process is a key component of predictive analytics. Whereas
logistic regression depends on feature selection/discovery being done beforehand,
Random Forest and GBM tree based machine learning approaches intrinsically enact
their feature selections.
 However, default options for Random Forest and GBM are biased towards continuous
variables, less favor of categorical and binary variables. Unbiased solution is very
computational intensive.
 We proposed a new approach that combines the strengths of intrinsic feature selection
from Random Forest and GBM to detect non-linear relationship, scaling, and interaction
items and apply these non-linear transformations into traditional approach. A 0-10% lift
is observed.