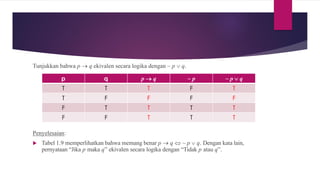
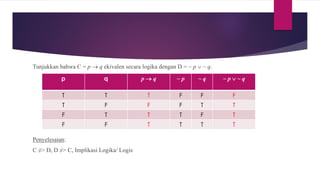
Dokumen ini membahas konsep-konsep dasar dalam teori himpunan, termasuk definisi, penulisan, jenis-jenis himpunan, serta operasi-operasi yang dapat dilakukan pada himpunan. Terdapat penjelasan mengenai himpunan semesta, himpunan kosong, himpunan bagian, dan operasi seperti gabungan, irisan, dan selisih. Selain itu, disertakan juga contoh-contoh untuk memperjelas penerapan teori himpunan dalam matematika.



















































![13
3. Representasi Relasi dengan Matriks
• Misalkan R adalah relasi dari A = {a1, a2, …, am} dan B =
{b1, b2, …, bn}.
• Relasi R dapat disajikan dengan matriks M = [mij],
b1 b2 bn
M =
mn
m
m
n
n
m
m
m
m
m
m
m
m
m
m
a
a
a
2
1
2
22
21
1
12
11
2
1
yang dalam hal ini
=
R
b
a
R
b
a
m
j
i
j
i
ij
)
,
(
,
0
)
,
(
,
1](https://image.slidesharecdn.com/12-220930132520-c79d4159/85/1_2-pdf-53-320.jpg)













































































































![Di dalam bahasa alami (bahasa percakapan manusia), seperti Bahasa Indonesia
dan Bahasa Inggris, terdapat hubungan sebab-akibat antara hipotesis dengan
konklusi, misalnya pada implikasi
“Jika suhu mencapai 80°C, maka alarm berbunyi.”
Implikasi seeprti ini adalah normal dalam Bahasa Indonesia. Tetapi, dalam penalaran
matematik, kita memandang implikasi lebih umum daripada implikasi dalam bahasa
alami. Konsep matematik mengenai implikasi independen dari hubungan sebab-akibat
antara hipotesis dan konklusi. Definisi kita mengenai implikasi adalah pada nilai
kebenarannya, bukan didasarkan pada penggunaan bahasa [ROS03]. Misalnya pada
implikasi
“Jika Paris adalah ibukota Perancis, maka 1 + 1 = 2”](https://image.slidesharecdn.com/12-220930132520-c79d4159/85/1_2-pdf-163-320.jpg)