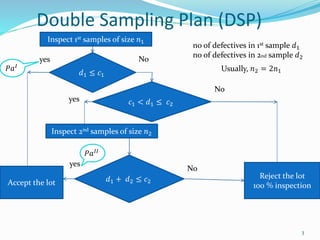
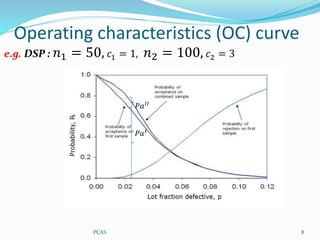
This document discusses a double sampling plan (DSP) acceptance sampling procedure. It defines key terms related to DSP including: probability of acceptance after the first (PaI) and second (PaII) samples, operating characteristics curve, average outgoing quality (AOQ), average outgoing quality limit (AOQL), average sample number (ASN), and average total inspection (ATI). It provides an example of calculating PaI, PaII, and Pa for a DSP with n1=50, c1=1, n2=100, c2=3 and incoming quality p=0.05. It also summarizes advantages and disadvantages of DSP compared to a single sampling plan.