Downloaded 62 times
Uploaded byDmitry Grapov
1 statistical analysis
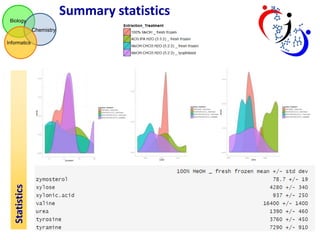
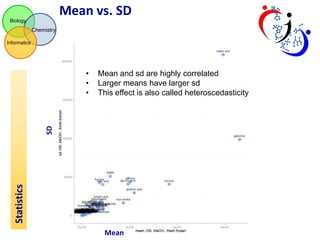
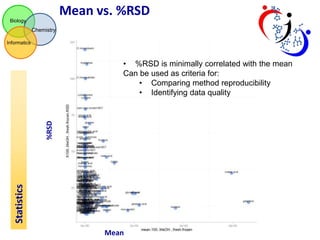
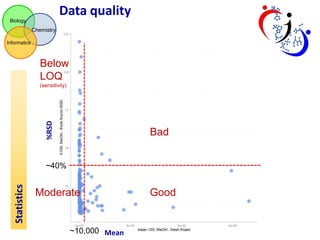
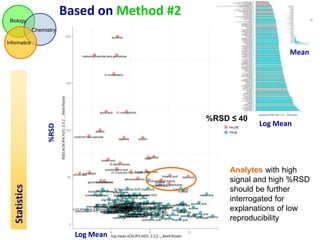
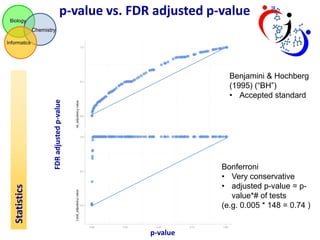
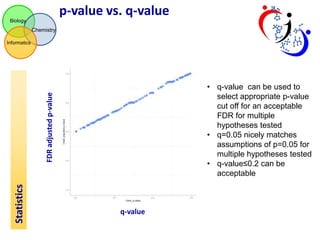
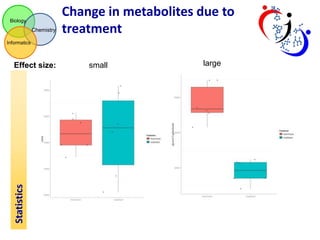
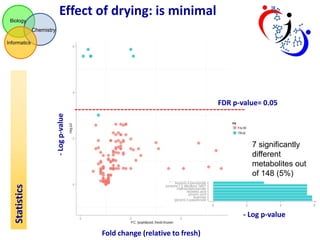
This document summarizes the analysis of different extraction and drying protocols for pumpkin leaf metabolites. It compares various metrics like mean, standard deviation, and percent relative standard deviation (%RSD) to identify the optimal sample processing method. Method #2, using acetonitrile, isopropanol and water in a 3:3:2 ratio, showed the lowest average %RSD and most metabolites below a 40% RSD cutoff, making it the optimal method. Statistical tests found minimal effect of drying on metabolite levels. A power analysis determined sample sizes needed to detect certain minimum effect sizes.
1 statistical analysis
- 1. Biology Chemistry Informatics Evaluation of sampleprocessing protocols for the analysis of pumpkin leaf metabolites Statistics Goals: Compare different extraction and drying protocols to identify the “optimal” sample processing approach Topics: 1. Data quality overview 2. Statistical comparisons 3. Power analysis
- 2. Data Quality Overview Biology Chemistry Informatics Goal:Calculate and visualize the summary statistics for each metabolite/treatment (Use DATA: Pumpkin data 1.csv) Calculate: 1. Mean and standard deviation (sd) 2. The percent relative standard deviation, %RSD, (sd/mean)*100 Statistics Visualize: 1. The relationship between mean vs. sd, mean and %RSD 2. Compare mean metabolite values for all treatments Exercises: 1. Describe the relationship between analyte mean and sd, mean and %RSD? 2. Describe what constitutes an “optimal” method? 3. Which extraction/treatment should be chosen to process further samples?
- 3.
- 4. Mean vs. SD Biology Chemistry Informatics Meanand sd are highly correlated Larger means have larger sd This effect is also called heteroscedasticity Statistics SD • • • Mean
- 5. Mean vs. %RSD Biology Chemistry Informatics Statistics %RSD •%RSD is minimally correlated with the mean Can be used as criteria for: • Comparing method reproducibility • Identifying data quality Mean
- 6. Qualities of %RSD Biology Chemistry Informatics • • • %RSD(also called the coefficient of variation or CV) is the sd (variation) scaled by the mean (magnitude). Removes the relationship between variation and magnitude Provides a single value which can be used to compare the variation of a measurement among different treatments/samples Statistics Showing the mean and sd of the %RSD for all metabolites for a given treatment
- 7.
- 8. Selecting the “optimal”method Biology Chemistry Informatics Optimal can be: 1. Lowest average %RSD for all measurements 2. Lowest %RSD for measurements of interest 3. Largest number of metabolites passing %RSD cutoff 4. Lowest average %RSD for all measurements passing %RSD cutoff Using strategy #4 for metabolites %RSD ≤ 40 Statistics Count Method #2 (ACN/IPA/water 3:3:2) looks optimal… %RSD (mean sd)
- 9. Based on Method#2 Biology Chemistry Informatics Mean %RSD %RSD ≤ 40 Log Mean Statistics Analytes with high signal and high %RSD should be further interrogated for explanations of low reproducibility Log Mean
- 10. Biology Chemistry Statistical comparison ofthe effects of sample drying Informatics Goals: identify the effect of treatment (fresh/lyophylized) on Methods #3-4 performance? (Use DATA: Pumpkin data 2.csv) Count %RSD (mean sd) Statistics Steps: 1. Use t-Test to compare metabolite means for each treatment 2. Correct for the false discovery rate (FDR) adjusted p-value 3. Estimate FDR (q-value) Visualize: 1. Relationship between p-value and FDR adjusted p-value 2. Relationship between FDR adjusted p-value and q-value 3. Box plots for highest and lowest p-value metabolites Questions: 1. When should you use a one-sample, two-sample or paired t-test, ANOVA? *return to 0-introduction
- 11. Hypothesis Testing Strategies Biology Chemistry Statistics Informatics •One sample t-Test is used to compare single value to a population mean • Two sample t-Test is used to compare 2 independent populations • Paired t-Test is used to compare the same population (intervention, repeated measures) • One-way ANOVA (analysis of variance) is used to compare n populations for one factor • Two-way ANOVA is used to compare n populations for 2 factors • ANCOVA (analysis of covariance) is used to adjust n populations for covariate (typically continuous) prior to testing for n factors • Mixed effects models are versatile analogue to linear model or ANOVA/ANCOVA and typically used to adjust for covariates or variance due to repeated measures *All of the above are parametric tests, and some of which have non-parametric analogues
- 12. p-value vs. FDRadjusted p-value Biology Chemistry Informatics FDR adjusted p-value Benjamini & Hochberg (1995) (“BH”) • Accepted standard Statistics Bonferroni • Very conservative • adjusted p-value = pvalue*# of tests (e.g. 0.005 * 148 = 0.74 ) p-value
- 13. p-value vs. q-value Biology Chemistry Informatics Statistics FDRadjusted p-value • q-value can be used to select appropriate p-value cut off for an acceptable FDR for multiple hypotheses tested • q=0.05 nicely matches assumptions of p=0.05 for multiple hypotheses tested • q-value≤0.2 can be acceptable q-value
- 14. Biology Chemistry Change in metabolitesdue to treatment Informatics Statistics Effect size: small large
- 15. Effect of drying:is minimal Biology Chemistry Informatics - Log p-value FDR p-value= 0.05 Statistics 7 significantly different metabolites out of 148 (5%) - Log p-value Fold change (relative to fresh)
- 16. Power analysis Biology Chemistry Informatics Goals: Usepower analysis to plan a follow up experiment to detect differences in metabolites due to treatment Steps: 1. Calculate effect size and power for three metabolites 2. Given the observed effect size calculate the number of samples needed to reach 80% power Statistics Questions: 1. How would you take FDR in to account?
- 17. Power analysis Biology Chemistry Informatics Statistics Scaled differencein means between treatments Ability to detect a difference when it exists (control false negative rate) Probability of being wrong when spotting a difference (control false positive rate)
- 18. Power analysis Biology Chemistry Informatics The minimumfold change (FC) in means observable by the study can be calculated using RSD and estimated effect size to reach 0.8 (80%) power given the population size Statistics RSD = 0.21 and effect size (EF) =1.2 We can observe a minimum of a 38% change in means at 0.8 power (p= 0.05).