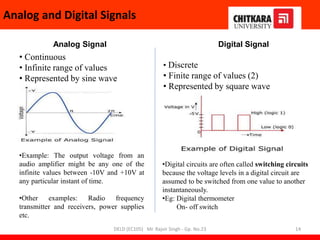
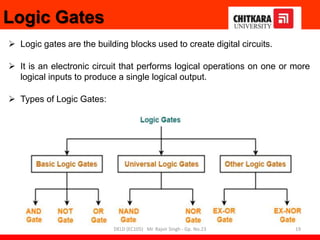
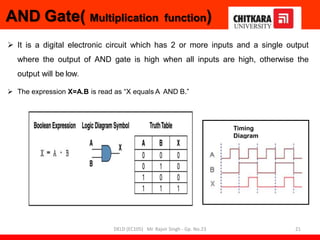
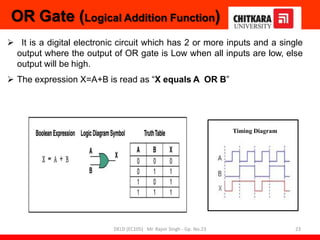
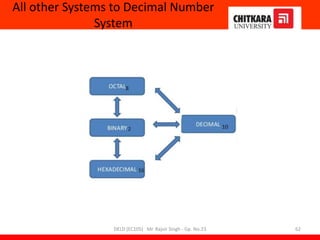
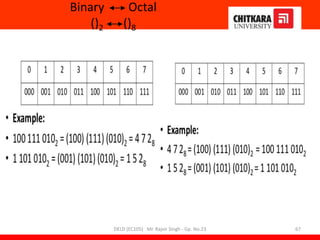
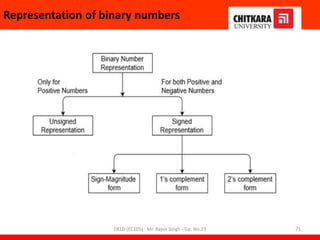
This document provides information about a Digital Electronics and Logic Design (DELD) course. It includes:
- The course name, code, semester, credits, and faculty member.
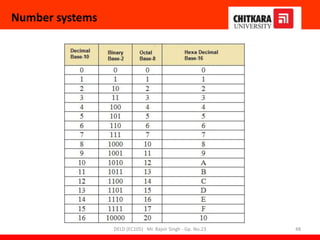
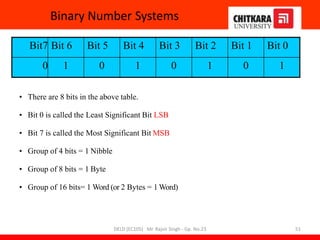
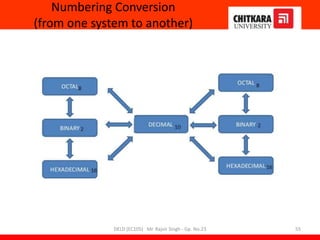
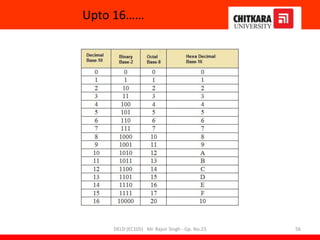
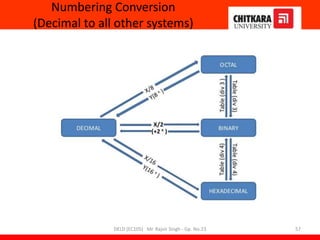
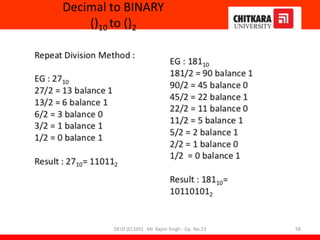
- An overview of the course content which teaches fundamentals of digital logic design, number systems, logic elements, circuit design and optimization.
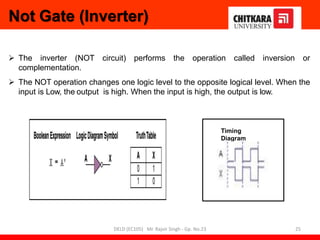
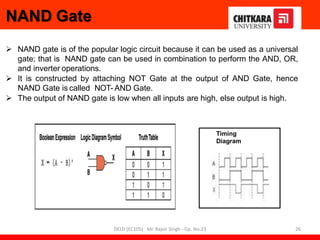
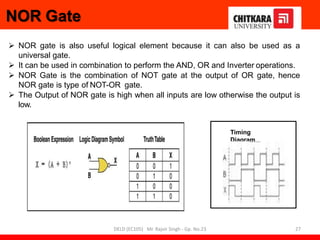
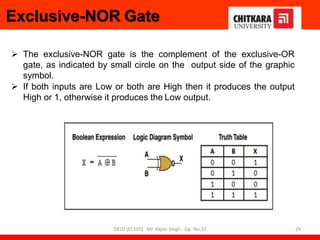
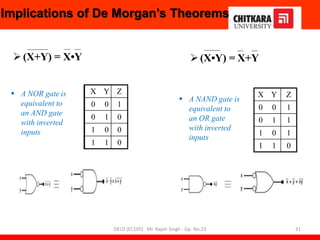
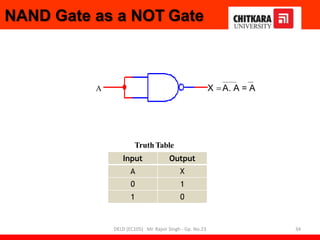
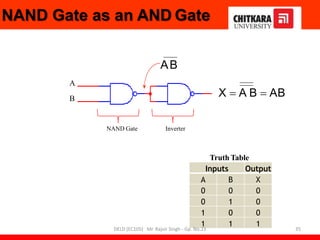
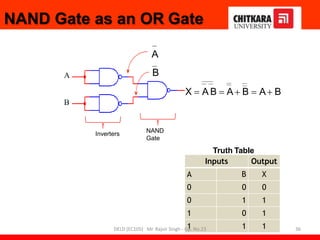
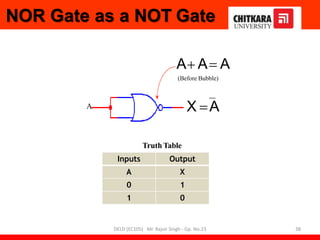
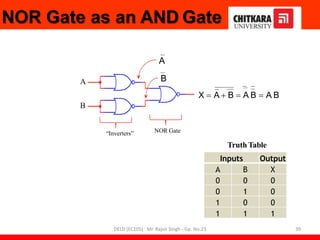
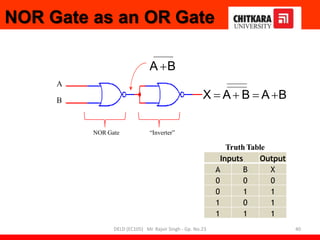
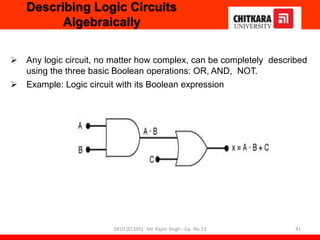
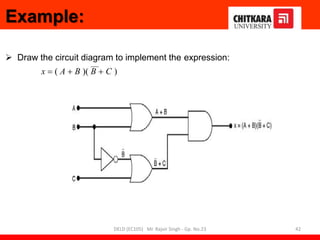
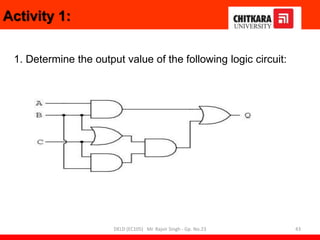
- Descriptions of logic gates like AND, OR, NOT, NAND and NOR gates along with their truth tables and diagrams.
- Details about the syllabus, course outcomes, recommended books and the content of the first unit on digital concepts and logic gates.