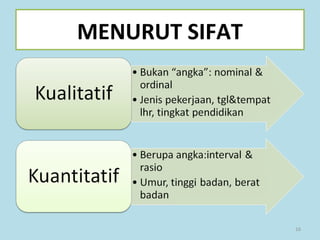
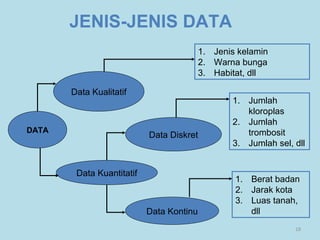
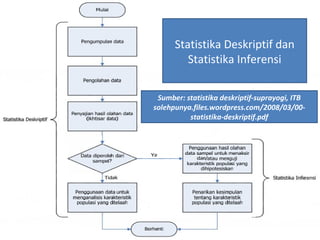
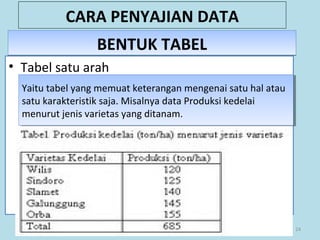
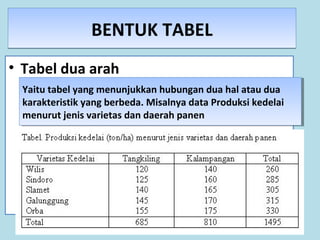
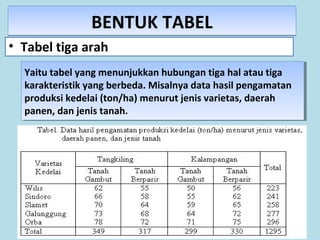
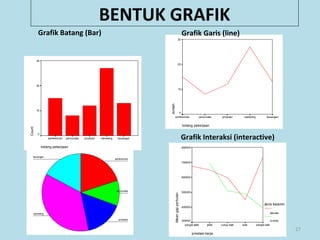
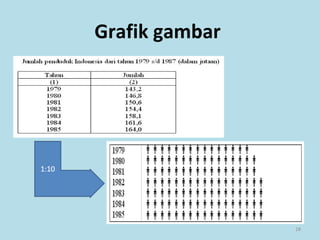
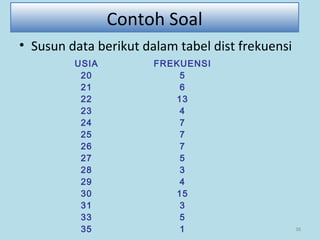
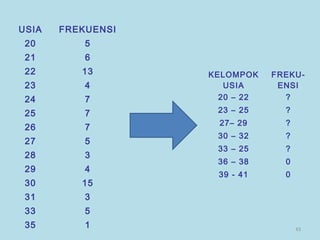
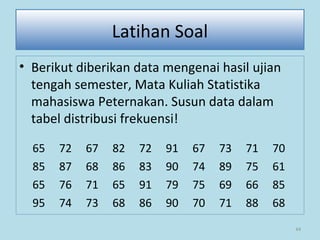
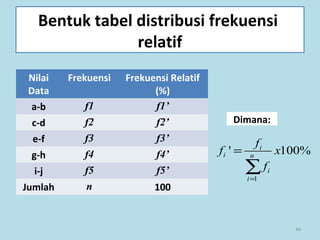
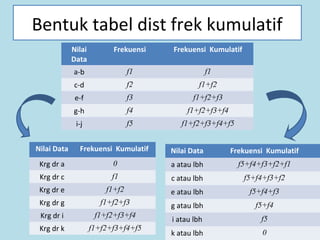
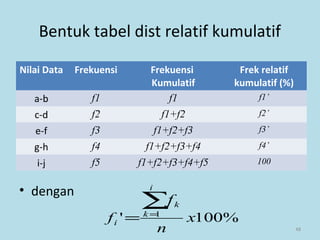
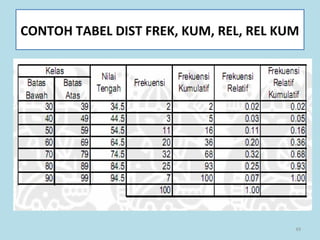
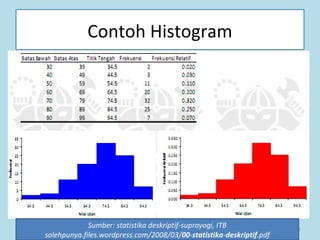
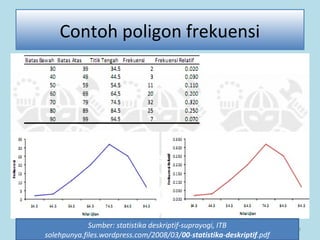
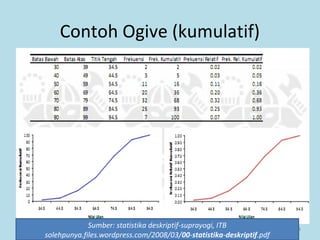
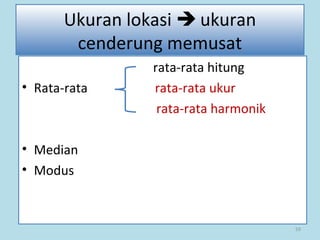
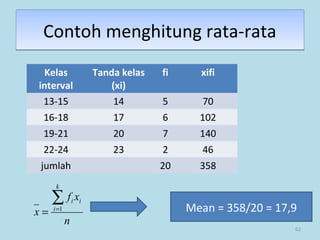
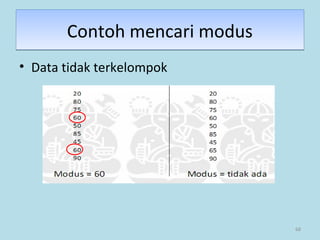
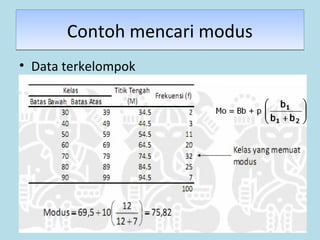
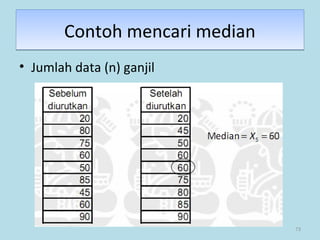
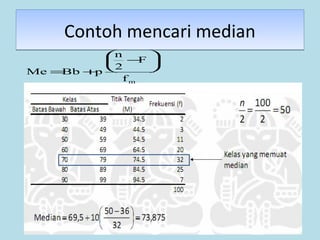
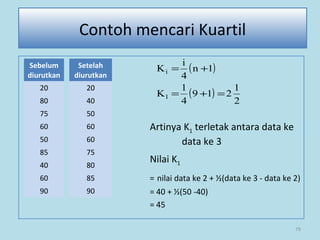
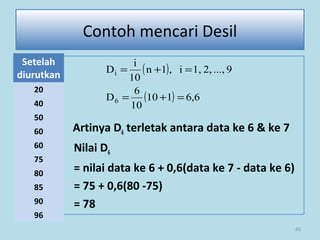
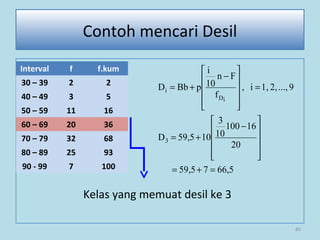
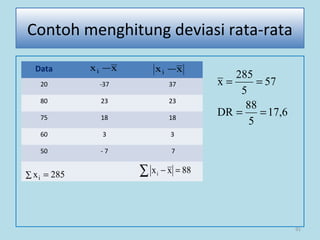
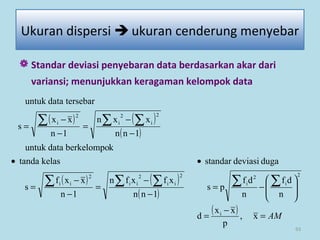
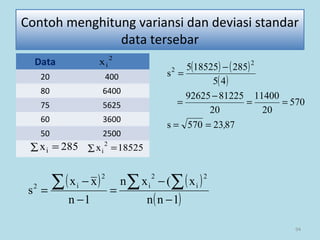
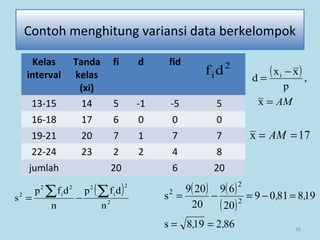
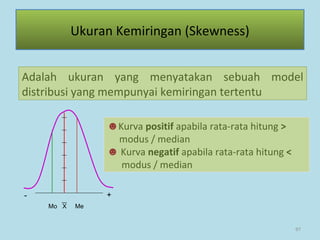
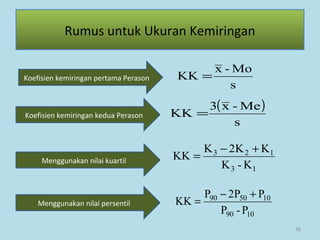
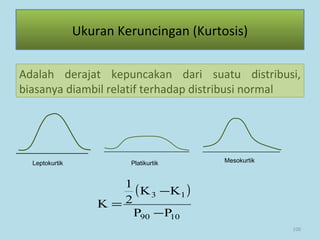
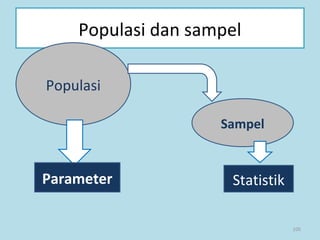
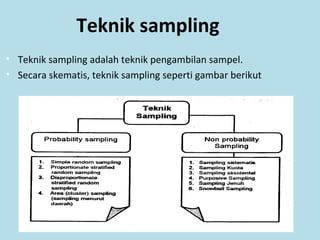
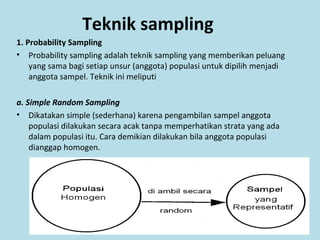
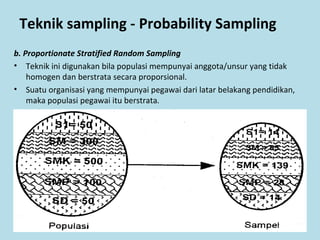
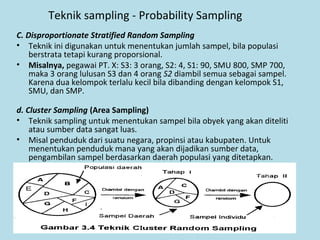
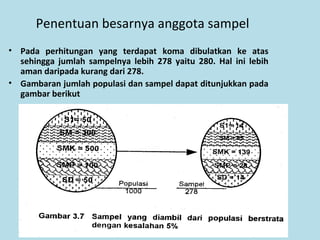
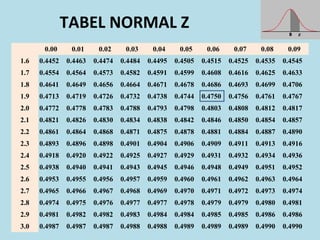
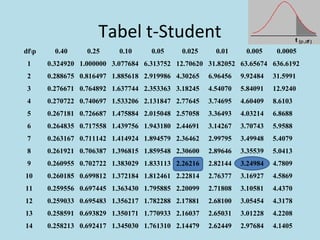
Dokumen ini membahas tentang statistika, termasuk pengertian, jenis-jenis data, metode pengumpulan, serta penyajian dan analisis data. Terdapat penjelasan mengenai statistik deskriptif dan inferensial, serta aplikasi di bidang biostatistika. Selain itu, dokumen ini menjelaskan langkah-langkah statistik dan jenis tabel distribusi frekuensi.

1. 1
STATISTIKA
DR. IR. LA ODE NAFIU, M.Si.
Prof. DR. IR. TAKDIR SAILI, M.Si.
LA ODE ARSAD SANI, S.Pt., M.Sc.
ACHMAD SELAMET AKU, S.Pt., M.Si.
JURUSAN PETERNAKAN
FPT-UHO

2. TUJUAN PEMBELAJARAN
1. Memahami pengertian statistika, serta jenis, tipe dan sifat
data
2. Memahami penyajian data
3. Memahami distribusi frekeuensi
4. Memahami ukuran pemusatan
5. Memahami jenis dan cara melakukan sampling serta
penentuan ukuran sampel
6. Memahami Distribusi peluang
7. Memahami penaksiaran parameter
8. Memahami pengujian hipotesis
9. Mampu menghitung korelasi dan regresi
10. Memahami dan menganalisis statistik non parametrik
2

3. PENDAHULUAN
3

4. PENGERTIAN
• Statistik:
- Suatu kumpulan angka yang tersusun lebih
dari satu angka
- Data yang diperoleh dari hasil observasi
berupa data cacahan atau data ukuran.
• Dalam statistika tercakup dua pekerjaan
penting, yaitu : Penyajian dan
penafsiran....DATA  informasi
4

5. PENGERTIAN
• Statistika adalah:
1.ilmu yang mempelajari tentang teknik
pengumpulan data, penyajian data dan
analisis data untuk penarikan kesimpulan
terhadap populasi
2.metode yang berhubungan dengan penyajian
dan penafsiran kejadian yang bersifat
peluang dalam suatu penyelidikan terencana
atau penelitian ilmiah
5

6. 6
Biostatistika yaitu penerapan metode statistika dalam
memecahkan permasalahan dalam bidang biologi
•Mencari deskripsi suatu variable
•Mencari hubungan antar variable
•Menentukan perbedaan respon akibat perlakuan yang
diberikan
Statistik diperlukan sbg alat utk membantu
memecahkan berbagai masalah melalui penelitian
Penelitian = penyelidikan/pencarian yg sistematik thd
kebenaran yg blm terungkap (Leedy, 1974)
PENGERTIAN

7. 7
Ciri-ciri penelitian :
• dimulai dg adanya pertanyaan
• membutuhkan pernyataan yg jelas
• membutuhkan perencanaan
• dilakukan secara bertahap
• mengajukan hipotesis
• mengemukakan fakta dan makna dg
benar
• bersifat sirkuler

8. 8
Dalam melakukan suatu penelitian harus
dilandasi dengan penggunaan metode
ilmiah
Syarat metode ilmiah:
•Dasar :- fakta/data reliable, valid, ternilai
- teori yg relevan
•Sifat : universal, obyektif. Jujur dan
terbuka
•Logis, kritis, analistis, dinamis dan inovatif

9. Data kasar (raw data) diperoleh dari
hasil pengukuran suatu variable
pada sample yg diambil dari suatu
populasi menggunakan teknik
pengambilan sample tertentu

10. Langkah-langkah kegiatan statistika utk
menangani data kasar :
1.Pengumpulan data
2.Pengolahan data (diurutkan atau
digolongkan)
3.Penyajian data dalam tabel atau grafik
4.Penafsiran sajian data
5.Analisa data
6.Penafsiran dan pengambilan kesimpulan
7.Pemanfaat penafsiran dan kesimpulan utk
penentuan kegiatan penelitian lbih lanjut

11. 11
Poin 1,2,3,4,7 disebut statistik deskriptif = stat.
Deduktif (tanpa analisis, tanpa generalisasi, tanpa
pengujian hipotesis, dan hanya melakukan
perhitungan-perhitungan saja)
Disajikan dalam bentuk tabel distribusi frekuensi
(mean, modus, median), bar-diagram, histogram,
polygon, dll
Poin 5,6 disebut statistik inferensial = stat. Induktif (dg
analisis, generalisasi, pengujian hipotesis)
Uji t,z, F

12. 12
TIPE DATA STATISTIKTIPE DATA STATISTIK
• Data nominal
• Data ordinal
• Data interval
• Data rasio
DATA NOMINAL :
Data berskala nominal adalah data yang diperoleh dengan
cara kategorisasi atau klasifikasi.
CIRI : posisi data setara
tidak bisa dilakukan operasi matematika (+, -, x, :)
CONTOH : jenis kelamin, jenis pekerjaan
KualitatifKualitatif
KuantitatifKuantitatif

13. 13
TIPE DATA STATISTIKTIPE DATA STATISTIK
DATA ORDINAL :
Data berskala ordinal adalah data yang diperoleh
dengan cara kategorisasi atau klasifikasi, tetapi di
antara data tersebut terdapat hubungan
CIRI : posisi data tidak setara
tidak bisa dilakukan operasi matematika (+, -, x, :)
CONTOH : kepuasan kerja (1= tidak puas; 2= kurang
pusat; 3=cukup puas; 4=puas; 5=sangat puas)

14. TIPE DATA STATISTIKTIPE DATA STATISTIK
DATA INTERVAL :
Data berskala interval adalah data yang diperoleh dengan cara
pengukuran, di mana jarak antara dua titik skala sudah
diketahui.
CIRI : Tidak ada kategorisasi
bisa dilakukan operasi matematika
CONTOH : temperatur yang diukur berdasarkan 0
C dan 0
F,
DATA INTERVAL :
Data berskala interval adalah data yang diperoleh dengan cara
pengukuran, di mana jarak antara dua titik skala sudah
diketahui.
CIRI : Tidak ada kategorisasi
bisa dilakukan operasi matematika
CONTOH : temperatur yang diukur berdasarkan 0
C dan 0
F,
DATA RASIO :
Data berskala rasio adalah data yang diperoleh dengan cara
pengukuran, di mana jarak antara dua titik skala sudah
diketahui dan mempunyai titik 0 absolut.
CIRI : tidak ada kategorisasi
bisa dilakukan operasi matematika
CONTOH : gaji, skor ujian, jumlah buku
DATA RASIO :
Data berskala rasio adalah data yang diperoleh dengan cara
pengukuran, di mana jarak antara dua titik skala sudah
diketahui dan mempunyai titik 0 absolut.
CIRI : tidak ada kategorisasi
bisa dilakukan operasi matematika
CONTOH : gaji, skor ujian, jumlah buku

15. 15
KLASIFIKASI JENIS DATA

16. 16
MENURUT SIFAT

17. DATA KUALITATIF
Data kualitatif = berbentuk kategori & atribut,
diperoleh dari hasil pengamatan
DATA KUANTITATIF
• berbentuk bilangan, diperoleh dari kegiatan
pengukuran
1. Data diskrit= diperoleh dengan cara menghitung
atau membilang, misal jumlah kursi per ruang ada
40 buah.
2. Data kontinyu= diperoleh dengan cara mengukur,
misal tinggi badan 165 cm
17
SIFAT DATA

18. 18
JENIS-JENIS DATA
DATA
Data Kualitatif
Data Kuantitatif
Data Diskret
Data Kontinu
1. Jenis kelamin
2. Warna bunga
3. Habitat, dll
1. Jumlah
kloroplas
2. Jumlah
trombosit
3. Jumlah sel, dll
1. Berat badan
2. Jarak kota
3. Luas tanah,
dll

19. CARA PENGUMPULAN DATA
• Wawancara
• Observasi langsung
• Angket
• Studi Pustaka
19

20. 20
• Statistika Deskriptif
• Statistika Inferensial
STATISTIKA MENURUT FUNGSINYA
Menggambarkan dan menganalisis kelompok
data yang diberikan tanpa penarikan
kesimpulan mengenai kelompok data yang
lebih besar
Penerapan metode statistik untuk menaksir
dan/atau menguji karakteristik populasi yang
dihipotesiskan berdasarkan data sampel

21. 21
Statistika Deskriptif dan
Statistika Inferensi
Sumber: statistika deskriptif-suprayogi, ITB
solehpunya.files.wordpress.com/2008/03/00-
statistika-deskriptif.pdf

22. PENYAJIAN DATA
22

23. 23
TUJUAN PENYAJIAN DATATUJUAN PENYAJIAN DATA
• Memberi gambaran yang sistematis tentang
peristiwa-peristiwa yang merupakan hasil
penelitian atau observasi,
• Data lebih cepat ditangkap dan dimengerti,
• Memudahkan dalam membuat analisis data,
dan
• Membuat proses pengambilan keputusan
dan kesimpulan lebih tepat, cepat, dan
akurat.

24. 24
BENTUK TABELBENTUK TABEL
• Tabel satu arah
Yaitu tabel yang memuat keterangan mengenai satu hal atau
satu karakteristik saja. Misalnya data Produksi kedelai
menurut jenis varietas yang ditanam.
Yaitu tabel yang memuat keterangan mengenai satu hal atau
satu karakteristik saja. Misalnya data Produksi kedelai
menurut jenis varietas yang ditanam.
CARA PENYAJIAN DATA

25. 25
BENTUK TABELBENTUK TABEL
• Tabel dua arah
Yaitu tabel yang menunjukkan hubungan dua hal atau dua
karakteristik yang berbeda. Misalnya data Produksi kedelai
menurut jenis varietas dan daerah panen
Yaitu tabel yang menunjukkan hubungan dua hal atau dua
karakteristik yang berbeda. Misalnya data Produksi kedelai
menurut jenis varietas dan daerah panen

26. 26
BENTUK TABELBENTUK TABEL
• Tabel tiga arah
Yaitu tabel yang menunjukkan hubungan tiga hal atau tiga
karakteristik yang berbeda. Misalnya data hasil pengamatan
produksi kedelai (ton/ha) menurut jenis varietas, daerah
panen, dan jenis tanah.
Yaitu tabel yang menunjukkan hubungan tiga hal atau tiga
karakteristik yang berbeda. Misalnya data hasil pengamatan
produksi kedelai (ton/ha) menurut jenis varietas, daerah
panen, dan jenis tanah.

27. 27
bidang pekerjaan
keuanganmarketingproduksipersonaliaadministrasi
Jumlah
30
20
10
0
keuangan
marketing
produksi
personalia
administrasi
prestasi kerja
sangat baikbaikcukup baikjeleksangat jelek
Meangajiperbulan
800000
700000
600000
500000
400000
300000
Jenis kelamin
laki-laki
w anita
Grafik Batang (Bar) Grafik Garis (line)
Grafik lingkaran (pie) Grafik Interaksi (interactive)
bidang pekerjaan
keuanganmarketingproduksipersonaliaadministrasi
Count
30
20
10
0
BENTUK GRAFIK

28. 28
Grafik gambar

29. ISTILAH DALAM STATISTIKA
• Obyek = benda hidup atau mati yg diuji unsur-unsur, sifat
dan kelakuannya melalui pengamatan, pengukuran dan
penilaian guna mendpt info atau nilai-nilai yg berguna
mengenai benda tsb
• VARIABEL
Suatu sifat dari obyek atau unsur dari obyek yg dpt diamati
atau diukur shg menghasilkan nilai, ukuran atau kriteria
lain yg dpt bervariasi
• VARIATE
Angka/nilai ukuran/keriteria lain yg dicapai suatu variabel
pada suatu individu atau unit statistik
• VARIASI
Adanya perbedaan antar nilai/variate/ukuran dll dari suatu
variabel pada populasi atau sampel
29

30. • VARIABILITAS
Kemungkinan utk bervariasi dr nilai suatu variable pd
suatu populasi atau sample
PARAMETER
suatu variabel terukur yg digunakan sbg kriteria utk
mengevaluasi suatu populasi atau sistem
• NILAI PARAMETRIK
suatu nilai dari suatu parameter yg diperoleh dari
perhitungan atau data sensus, masih harus di analisis.
NILAI STATISTIK
suatu nilai dari suatu parameter yg diperoleh dari
perhitungan sampel atau data sensus.
30
ISTILAH DALAM STATISTIKA

31. Statistika Parametrik:
• Membutuhkan pengukuran kuantitatif dengan
data interval atau rasio
• mempertimbangkan jenis sebaran/distribusi
data, yaitu apakah data menyebar normal atau
tidak.
• Contoh metode statistika parametrik: uji-z (1
atau 2 sampel), uji-t (1 atau 2 sampel), korelasi
pearson, Perancangan Percobaan (1 or 2-way
ANOVA parametrik), dll.
JENIS STATISTIKA

32. Statistika Nonparametrik:
• Membutuhkan data dengan data ordinal dan
nominal
• Merupakan statistika bebas sebaran (tdk
mensyaratkan bentuk sebaran parameter
populasi, baik normal atau tidak).
• Contoh metode Statistika non-
parametrik:Binomial test, Chi-square test,
Median test, Friedman Test, dll.
32
ISTILAH DALAM STATISTIKA

33. PERTANYAAN
1. Uraikan perbedaan tipe data interval dan
rasio dan berikan contoh
2. Uraikan perbedaan sifat data kualitatif dan
data kuantitatif dan berikan contoh
3. Jelaskan tujuan penyajian data
4. Uraikan perbedaan statistika deskriptif dan
inferensia
5. Jelaskan macam-macam bentuk penyajian
data secara grafik dan berikan contohnya
33

34. 34
DISTRIBUSI FREKUENSI

35. 35
Distribusi Frekuensi
• Bentuk pengelompokan data untuk
menggambarkan distribusi data
• Dapat dinyatakan dalam
 bentuk tabel distribusi frekuensi
 histogram atau poligon frekuensi

36. 36
Prosedur Umum Penyusunan
Tabel Dist Frekuensi
• Tentukan banyaknya kelas
• Tentukan lebar kelas
• Hitung frekuensi untuk setiap kelas

37. 37
Contoh tabel dist frekuensi
KELOMPOK FREKUENSI
Kelompok ke-1 f1
Kelompok ke-2 f2
Kelompok ke-3 f3
Kelompok ke-i fi
Kelompok ke-k fk
k
n = Σ fi
i=1
Pendidikan Frekuensi
S1 62
S2 19
S3 9
90
k
n = Σ fi = f1 + f2 + f3 +….. + fi + …… + fk
i=1

38. 38
Contoh Soal
• Susun data berikut dalam tabel dist frekuensi
USIA FREKUENSI
20 5
21 6
22 13
23 4
24 7
25 7
26 7
27 5
28 3
29 4
30 15
31 3
33 5
35 1

39. 39
Langkah-langkah
• Tentukan rentang
• Tentukan banyak kelas (k)
• Tentukan panjang kelas (p)
RENTANG: NILAI DATA TERBESAR – NILAI DATA TERKECILRENTANG: NILAI DATA TERBESAR – NILAI DATA TERKECIL
ATURAN STURGES:
k = 1 + (3,322)(log n)
ATURAN STURGES:
k = 1 + (3,322)(log n)
p = RENTANG/kp = RENTANG/k

40. 40
Catatan tentang panjang kelas
DATA PANJANG KELAS (p)

41. 41
Lanjutan langkah-langkah
• Tentukan nilai ujung bawah kelas interval
pertama
• Masukkan semua data ke dalam interval kelas
Boleh mengambil nilai data terkecil
atau nilai data yang lebih kecil dari nilai data
terkecil
Boleh mengambil nilai data terkecil
atau nilai data yang lebih kecil dari nilai data
terkecil

42. 42
Kembali ke contoh..
Membuat distribusi frekuensi :
1. Mencari rentang  35 – 20 = 15
2. Menentukan banyak kelas  k = 1 + 3,3 log n  7 atau
8
3. Menentukan panjang kelas  p = 15/7 = 2,5  2 atau 3
KELOMPOK USIA FREKUENSI
20 – 21 11
22 – 23 17
24 – 25 14
26 – 27 12
28 – 29 7
30 – 31 18
32 - 33 5
34 - 35 1
USIA FREKUENSI
20 5
21 6
22 13
23 4
24 7
25 7
26 7
27 5
28 3
29 4
30 15
31 3
33 5
35 1

43. 43
USIA FREKUENSI
20 5
21 6
22 13
23 4
24 7
25 7
26 7
27 5
28 3
29 4
30 15
31 3
33 5
35 1
KELOMPOK
USIA
FREKU-
ENSI
20 – 22 ?
23 – 25 ?
27– 29 ?
30 – 32 ?
33 – 25 ?
36 – 38 0
39 - 41 0

44. 44
• Berikut diberikan data mengenai hasil ujian
tengah semester, Mata Kuliah Statistika
mahasiswa Peternakan. Susun data dalam
tabel distribusi frekuensi!
65 72 67 82 72 91 67 73 71 70
85 87 68 86 83 90 74 89 75 61
65 76 71 65 91 79 75 69 66 85
95 74 73 68 86 90 70 71 88 68
Latihan Soal

45. 45
Macam-macam tabel distribusi
frekuensi

46. 46
Bentuk tabel distribusi frekuensi
relatif
Nilai
Data
Frekuensi Frekuensi Relatif
(%)
a-b f1 f1’
c-d f2 f2’
e-f f3 f3’
g-h f4 f4’
i-j f5 f5’
Jumlah n 100
1
' 100%i
i n
i
i
f
f x
f
=
=
∑
Dimana:

47. 47
Bentuk tabel dist frek kumulatif
Nilai
Data
Frekuensi Frekuensi Kumulatif
a-b f1 f1
c-d f2 f1+f2
e-f f3 f1+f2+f3
g-h f4 f1+f2+f3+f4
i-j f5 f1+f2+f3+f4+f5
Nilai Data Frekuensi Kumulatif
Krg dr a 0
Krg dr c f1
Krg dr e f1+f2
Krg dr g f1+f2+f3
Krg dr i f1+f2+f3+f4
Krg dr k f1+f2+f3+f4+f5
Nilai Data Frekuensi Kumulatif
a atau lbh f5+f4+f3+f2+f1
c atau lbh f5+f4+f3+f2
e atau lbh f5+f4+f3
g atau lbh f5+f4
i atau lbh f5
k atau lbh 0

48. 48
Bentuk tabel dist relatif kumulatif
• dengan
Nilai Data Frekuensi Frekuensi
Kumulatif
Frek relatif
kumulatif (%)
a-b f1 f1 f1’
c-d f2 f1+f2 f2’
e-f f3 f1+f2+f3 f3’
g-h f4 f1+f2+f3+f4 f4’
i-j f5 f1+f2+f3+f4+f5 100
%100' 1
x
n
f
f
i
k
k
i
∑=
=

49. 49
CONTOH TABEL DIST FREK, KUM, REL, REL KUM

50. 50
Macam-macam bentuk diagram
• Data tidak terkelompok : diagram batang,
diagram lingkaran, garis, gambar (simbol)
• Data terkelompok : histogram dan poligon
frekuensi, ogive

51. 51
Histogram dan poligon frekuensi
• Histogram mrpk bentuk diagram batng yg
digunakan untuk menggambarkan dist
frekuensi
• Poligon (kurva) frekuensi mrpk bentuk
diagram garis yg digunakan utk
menggambarkan dist frekuensi

52. 52
Contoh Histogram
Sumber: statistika deskriptif-suprayogi, ITB
solehpunya.files.wordpress.com/2008/03/00-statistika-deskriptif.pdf

53. 53
Contoh poligon frekuensi
Sumber: statistika deskriptif-suprayogi, ITB
solehpunya.files.wordpress.com/2008/03/00-statistika-deskriptif.pdf

54. 54
Contoh Ogive (kumulatif)
Sumber: statistika deskriptif-suprayogi, ITB
solehpunya.files.wordpress.com/2008/03/00-statistika-deskriptif.pdf

55. 55
Catatan tentang batas atas dan bawah
• Batas bawah (bb) = ujung bwh – ketelitian
data yang digunakan
• Batas atas (ba) = ujung atas + ketelitian data
yg digunakan
Data Ketelitian yang digunakan
Bil bulat 0,5
Bil satu desimal 0,05
Bil dua desimal 0,005
dst

56. 56
Catatan tentang titik tengah
(tanda kelas)
Titik tengah = ½ (ujung bawah + ujung atas)Titik tengah = ½ (ujung bawah + ujung atas)

57. 57
UKURAN PEMUSATANUKURAN PEMUSATAN

58. 58
Statistik
• Ukuran lokasi (pemusatan)
• Ukuran dispersi (sebaran)
• Ukuran kemiringan
• Ukuran keruncingan

59. 59
Ukuran lokasi  ukuran
cenderung memusat
rata-rata hitung
• Rata-rata rata-rata ukur
rata-rata harmonik
• Median
• Modus

60. 60
Rata-rata hitung data tersebar
• Data tersebar (tdk berkelompok)
n
x
x
n
i
i∑=
= 1

61. 61
Rata-rata hitung data terkelompok
1. Tanda kelas 2. rata-rata duga
xi : titik tengah kelas AM : titik tengah kelas
interval ke-i interval (pilih sbrg)
p : panjang kelas intv
n
xf
x
k
i
ii∑=
= 1
n
df
pAMx
k
i
ii∑=
+= 1
p
AMx
d i
i
−
=

62. 62
Contoh menghitung rata-rataContoh menghitung rata-rata
Mean = 358/20 = 17,9
Kelas
interval
Tanda kelas
(xi)
fi xifi
13-15 14 5 70
16-18 17 6 102
19-21 20 7 140
22-24 23 2 46
jumlah 20 358
n
xf
x
k
i
ii∑=
= 1

63. 63
Contoh menghitung rata-rataContoh menghitung rata-rata
Kelas interval Tanda kelas (xi) fi di fidi
13-15 14 5 (14-20)/3 = -2 -10
16-18 17 6 -1 -6
19-21 20 7 0 0
22-24 23 2 1 2
jumlah 20 -14
Mean = 20+ (3)(-14)/20 =20 – 2,1 = 17,9
AM Yg
dipilih
n
df
pAMx
k
i
ii∑=
+= 1
p
AMx
d i
i
−
=

64. 64
Rata-rata ukur dan harmonis
• Rata-rata ukur
dimana dan seterusnya
• Rata-rata harmonis
n
nxxxU .... 21=
4
3
3
2
2
1
x
x
x
x
x
x
==
∑=
= n
i ix
n
Rh
1
1

65. RATA-RATA UKUR
• Keterangan:
U = rata-rata ukur (rata-rata geometrik)
n = banyaknya sampel
Π = Huruf kapital π (pi) yang menyatakan jumlah dari hasil kali unsur-unsur data.
Rata-rata geometrik sering digunakan dalam bisnis dan ekonomi untuk
menghitung rata-rata tingkat perubahan, rata-rata tingkat pertumbuhan, atau
rasio rata-rata untuk data berurutan tetap atau hampir tetap atau untuk rata-rata
kenaikan dalam bentuk persentase.
• 1. Rata-Rata Ukur data Tunggal
• Contoh 1:
Berapakah rata-rata ukur dari data 2, 4, 8?
• Jawab:
»
» ATAU
65

66. Rata-rata Harmoni
Contoh:
• Tuan A melakukan perjalanan dengan kereta dari Bandung ke Sidoarjo
pulang pergi. Bandung ke Sidoarjo berkecepatan 90 km/jam, tetapi
waktu pulang mampir dulu ke yagyakarta dengan kecepatan 70 km/jam,
kemudian hari berikutnya dilanjutkan lagi perjalanan menuju Bandung
dengan kecepatan 80 km/jam, berapakah kecepatan rata rata ?
Penyelesaian:
* Kecepatan Pertama X1 = 90 km / jam : * Kecepatan Kedua X2= 70 km /
jam
* Kecepatan Ketiga X3 = 80 km / jam: n = 3
66
0,0143

67. 67
Modus
• Data kualitatif  gejala yang sering terjadi
• Data kuantitatif  angka yang sering muncul

68. 68
Contoh mencari modusContoh mencari modus
• Data tidak terkelompok

69. 69
Modus pada data terkelompok
Mo = Bb + p
dengan
Bb = batas bawah kelas interval yang mempunyai frekuensi
tertinggi
b1 = selisih frekuensi tertinggi dengan frekuensi dari kelas
interval yang lebih rendah.
b2 = selisih frekuensi tertinggi dengan frekuensi dari kelas
interval yang lebih tinggi.
p = panjang kelas.






+ 21
1
bb
b

70. 70
• Data terkelompok
Contoh mencari modusContoh mencari modus

71. 71
Median untuk data tidak
terkelompok
• Jika jumlah data (n) genap
•
• Jika jumlah data (n) ganjil
Me =
2
2
2n
-kedatanilai
2
n
-kedatanilai 




 +
+





Me =





 +
2
1n
-kedatanilai
Data harus diurutkan dulu dari terkecil ke terbesar

72. 72
Contoh mencari medianContoh mencari median
• Jumlah data (n) genap

73. 73
• Jumlah data (n) ganjil
Contoh mencari medianContoh mencari median

74. 74
Median data terkelompok
dengan
Bb : batas bawah kelas interval yang mengandung Me
fm : frekuensi kelas interval yang mengandung Me
F : frekuensi kumulatif sebelum kelas interval
yang mengandung Me
p : panjang kelas interval
mf
F
2
n
pBbMe






−
+=
Letak Me harus paling sedikit mencapai frekuensi setengah dari jumlah
data seluruhnya
Letak Me harus paling sedikit mencapai frekuensi setengah dari jumlah
data seluruhnya

75. 75
Contoh mencari medianContoh mencari median
mf
F
2
n
pBbMe






−
+=

76. 76
Hubungan Mean, Modus dan Median
Hubungan empiris antara ketiganya:
Mo +2 M = 3Me

77. • Kuartil
• Desil
• Persentil
77
Ukuran dispersi  ukuran cenderung menyebar

78. 78
Kuartil untuk data tidak berkelompok
dengan
Ki : letak kuartil ke i
n : banyaknya data
( ) 32,1,i,1n
4
i
Ki =+=

79. 79
Artinya K1 terletak antara data ke
2 dan data ke 3
Nilai K1
= nilai data ke 2 + ½(data ke 3 - data ke 2)
= 40 + ½(50 -40)
= 45
Contoh mencari Kuartil
Sebelum
diurutkan
20
80
75
60
50
85
40
60
90
Setelah
diurutkan
20
40
50
60
60
75
80
85
90
( )
( )
2
1
219
4
1
K
1n
4
i
K
1
i
=+=
+=

80. 80
dengan
Ki : letak kuartil ke i
Bb : batas bawah kelas interval yang mengandung Ki
fK : frekuensi kelas interval yang mengandung Ki
F : frekuensi kumulatif sebelum kelas interval yang
mengandung Ki
p : panjang kelas interval
32,1,i,
f
Fn
4
i
pBbK
iK
i =










−
+=
Kuartil data berkelompok

81. 81
Contoh mencari Kuartil
Kelas yang memuat kuartil ke 3
Interval f f. kum
30 – 39 2 2
40 – 49 3 5
50 – 59 11 16
60 – 69 20 36
70 – 79 32 68
80 – 89 25 93
90 - 99 7 100
82,32,879,5
25
68100
4
3
1079,5K
32,1,i,
f
Fn
4
i
pBbK
3
iK
i
=+=










−
+=
=










−
+=

82. 82
Desil untuk data tidak berkelompok
dengan
Di : letak desil ke i
n : banyaknya data
( ) 9...,2,1,i,1n
10
i
Di =+=

83. Artinya D6 terletak antara data ke 6 & ke 7
Nilai D6
= nilai data ke 6 + 0,6(data ke 7 - data ke 6)
= 75 + 0,6(80 -75)
= 78
83
Contoh mencari Desil
Setelah
diurutkan
20
40
50
60
60
75
80
85
90
96
( )
( ) ,66110
10
6
D
9...,2,1,i,1n
10
i
D
6
i
=+=
=+=

84. dengan
Di : letak desil ke i
Bb : batas bawah kelas interval yang mengandung Di
fD : frekuensi kelas interval yang mengandung Di
F : frekuensi kumulatif sebelum kelas interval yang
mengandung Di
p : panjang kelas interval
84
Desil data berkelompok
9...,2,1,i,
f
Fn
10
i
pBbD
iD
i =










−
+=

85. Kelas yang memuat desil ke 3
85
Contoh mencari Desil
Interval f f.kum
30 – 39 2 2
40 – 49 3 5
50 – 59 11 16
60 – 69 20 36
70 – 79 32 68
80 – 89 25 93
90 - 99 7 100 66,5759,5
20
16100
10
3
1059,5D
9...,2,1,i,
f
Fn
10
i
pBbD
3
iD
i
=+=










−
+=
=










−
+=

86. dengan
Pi : letak persentil ke i
n : banyaknya data
86
Persentil untuk data tidak berkelompok
( ) 99...,2,1,i,1n
100
i
Pi =+=

87. Artinya P57 terletak antara data ke 6 & ke 7
Nilai P57
= nilai data ke 6 + 0,27(data ke 7 - data ke 6)
= 75 + 0,27(80 -75)
= 76,35
87
Contoh mencari Persentil
Setelah
diurutkan
20
40
50
60
60
75
80
85
90
96
( )
( ) 6,27110
100
57
P
99...,2,1,i,1n
100
i
P
57
i
=+=
=+=

88. dengan
Pi : letak persentil ke i
Bb : batas bawah kelas interval yang mengandung Pi
fP : frekuensi kelas interval yang mengandung Pi
F : frekuensi kumulatif sebelum kelas interval yang
mengandung Pi
88
Persentil data berkelompok
99...,2,1,i,
f
Fn
100
i
pBbP
iP
i =










−
+=

89. 89
Contoh mencari Desil
Kelas yang memuat persentil ke 96
Interval f f.kum
30 – 39 2 2
40 – 49 3 5
50 – 59 11 16
60 – 69 20 36
70 – 79 32 68
80 – 89 25 93
90 - 99 7 100
93,794,295,89P
7
93100
100
96
105,89P
99...,2,1,i,
f
Fn
100
i
pBbP
i
96
P
i
i
=+=










−
+=
=










−
+=

90. 90
Ukuran Dispersi (
Range
Deviasi rata-rata
Ukuran dispersi  ukuran cenderung menyebar
Range = Nilai Maksimum – Nilai Minimum
n
xx
DR i∑ −
=

91. 91
Contoh menghitung deviasi rata-rata
Data
20 -37 37
80 23 23
75 18 18
60 3 3
50 - 7 7
6,17
5
88
DR
57
5
285
x
==
==
xxi − xxi −
285xi =∑
88xxi =−∑

92.  Variansi : penyebaran berdasarkan jumlah kuadrat
simpangan data terhadap rata-ratanya; melihat
ketidaksamaan sekelompok data
92
Ukuran dispersi  ukuran cenderung menyebar
( ) ( )
( )
( ) ( )
( )
( )
( ) AM=
−
=
−=
−
−
=
−
−
=
••
−
−
=
−
−
=
∑∑∑ ∑∑
∑ ∑∑
x
p
xx
d
n
dfp
n
dfp
s
1nn
xfxfn
1n
xxf
s
dugavariansikelastanda
kberkelompodatauntuk
1nn
x(xn
1n
xx
s
tersebardatauntuk
i
2
2
i
22
i
2
2
2
ii
2
ii
2
ii2
2
i
2
i
2
i2

93.  Standar deviasi penyebaran data berdasarkan akar dari
variansi; menunjukkan keragaman kelompok data
93
Ukuran dispersi  ukuran cenderung menyebar
( ) ( )
( )
( ) ( )
( )
( ) AM=
−
=








−=
−
−
=
−
−
=
••
−
−
=
−
−
=
∑∑∑ ∑∑
∑ ∑∑
x,
p
xx
d
n
df
n
df
ps
1nn
xfxfn
1n
xxf
s
dugadeviasistandarkelastanda
kberkelompodatauntuk
1nn
xxn
1n
xx
s
tersebardatauntuk
i
2
i
2
i
2
ii
2
ii
2
ii
2
i
2
i
2
i

94. 94
Contoh menghitung variansi dan deviasi standar
data tersebar
Data
20 400
80 6400
75 5625
60 3600
50 2500
( ) ( )
( )
8723570s
570
20
11400
20
8122592625
45
285185255
s
2
2
,==
==
−
=
−
=
2
ix
∑ =18525x
2
i∑ = 285xi
( ) ( )
( )1nn
x(xn
1n
xx
s
2
i
2
i
2
i2
−
−
=
−
−
=
∑ ∑∑

95. 95
Kelas
interval
Tanda
kelas (xi)
fi xifi
13-15 14 5 196 70 980
16-18 17 6 289 102 1734
19-21 20 7 400 140 2800
22-24 23 2 529 46 1058
jumlah 20 358 6572
Contoh menghitung variansi dan deviasi standar
data berkelompok
2
ix 2
iixf
( ) ( )
( )
942628s
628
380
3276
380
128164131440
1920
358657220
s
2
2
,,
,
==
==
−
=
−
=
( ) ( )
( )1nn
xfxfn
1n
xxf
s
2
ii
2
ii
2
ii2
−
−
=
−
−
=
∑ ∑∑

96. 96
Contoh menghitung variansi data berkelompok
17x == AM
Kelas
interval
Tanda
kelas
(xi)
fi d fid
13-15 14 5 -1 -5 5
16-18 17 6 0 0 0
19-21 20 7 1 7 7
22-24 23 2 2 4 8
jumlah 20 6 20
2
idf
( ) ( )
( )
862198s
1988109
20
69
20
209
s 2
2
2
,,
,,
==
=−=−=
( )
2
2
i
22
i
2
2
n
dfp
n
dfp
s
∑∑ −=
( )
AM=
−
=
x
,
p
xx
d i

97. 97
Ukuran Kemiringan (Skewness)
Adalah ukuran yang menyatakan sebuah model
distribusi yang mempunyai kemiringan tertentu
Mo X Me
+-
☻Kurva positif apabila rata-rata hitung >
modus / median
☻ Kurva negatif apabila rata-rata hitung <
modus / median

98. 98
Rumus untuk Ukuran Kemiringan
s
Mo-x
KK =Koefisien kemiringan pertama Perason
Koefisien kemiringan kedua Perason
( )
s
Me-x3
KK =
Menggunakan nilai persentil
Menggunakan nilai kuartil
K-K
KK2K
KK
13
123 +−
=
P-P
PP2P
KK
1090
105090 +−
=

99. • Jika koefisien kemiringan < nol, maka bentuk
distribusinya negatif
• Jika koefisien kemiringan = nol, maka bentuk
distribusinya simetrik
• Jika koefisien kemiringan >nol, maka bentuk
distribusinya positif
99
Kriteria untuk mengetahui model distribusi dari
koefisien kemiringan

100. 100
Ukuran Keruncingan (Kurtosis)
Adalah derajat kepuncakan dari suatu distribusi,
biasanya diambil relatif terhadap distribusi normal
Leptokurtik Platikurtik Mesokurtik
( )
PP
KK
2
1
K
1090
13
−
−
=

101. • Jika koefisien kurtosis kurang dari 0,263 maka
distribusinya adl platikurtik
• Jika koefisien kurtosis sama dengan 0,263
maka distribusinya adl mesokurtik
• Jika koefisien kurtosis lebih dari 0,263 maka
distribusinya adl leptokurtik
101
Kriteria untuk mengetahui model distribusi dari
koefisien kurtosis

102. 102
Contoh menghitung koefisien kemiringan dan
ukuran keruncingan
Kelas
interval
Tanda
kelas (xi)
fi
13-15 14 5
16-18 17 6
19-21 20 7
22-24 23 2
jumlah 20
( )
( )
( )
( )
( ) 21,5
7
11-18
3518P
13,7
5
0-2
3512P
2120
7
11-15
3518K
18
6
5-10
3515K
15,5
5
0-5
3512K
90
10
3
2
1
=+=
=+=
=+=
=+=
=+=
,
,
,,
,
,
( )
( )
300
87
3552
713521
5152120
2
1
K
060
714
290
5152120
515182-20,21
KK
,
,
,
,,
,,
,
,
,
,,
,
==
−
−
=
−=
−
=
−
+
=
Model
Distribusi ?

103. 103
Latihan Soal
Diketahui data seperti di bawah ini.
15 25 21 16 20 17 19 25 21 15 17 16 19 20 17
20 15 25 15 21 19 16 17 25 19 21 20 19 19 21
17 20 16 21 20 21 16 20 17 19 20 19 17 21 19
20 16 19 19 17 20 21 19 19 21 19 17 20 19 15
1. Buatlah : Distribusi frek, dist frek kumulatif, dist frek relatif,
dist frek relatif kumulatif
2. Gambarlah histogram dan poligon dari dist frek kumulatif
tersebut
3. Tentukan Mean, Median, Modus
4. Kuartil, Desil, Persentil

104. POPULASI DAN SAMPEL
104

105. 105
Populasi dan sampel
Populasi
Sampel
Parameter Statistik

106. 106
Populasi dan sampel
Populasi adalah data kuantitatif yang
menjadi objek telaah
Sampel adalah bagian dari populasi
Parameter adalah ukuran yang
mencerminkan karakteristik dari populasi
Statistik adalah ukuran yang mencerminkan
karakteristik dari sampel

107. POPULASI DAN SAMPEL
• Populasi
– Populasi adalah wilayah generalisasi yang terdiri atas;
obyek/subyek yang mempunyai kuantitas dan
karakteristik tertentu yang ditetapkan oleh peneliti
untuk dipelajari dan kemudian ditarik kesimpulannya.
• Sampel
– Sampel adalah sebagian dari jumlah dan karateristik
yang dimiliki oleh populasi.

108. Teknik sampling
• Teknik sampling adalah teknik pengambilan sampel.
• Secara skematis, teknik sampling seperti gambar berikut

109. Teknik sampling
1. Probability Sampling
• Probability sampling adalah teknik sampling yang memberikan peluang
yang sama bagi setiap unsur (anggota) populasi untuk dipilih menjadi
anggota sampel. Teknik ini meliputi
a. Simple Random Sampling
• Dikatakan simple (sederhana) karena pengambilan sampel anggota
populasi dilakukan secara acak tanpa memperhatikan strata yang ada
dalam populasi itu. Cara demikian dilakukan bila anggota populasi
dianggap homogen.

110. Teknik sampling - Probability Sampling
b. Proportionate Stratified Random Sampling
• Teknik ini digunakan bila populasi mempunyai anggota/unsur yang tidak
homogen dan berstrata secara proporsional.
• Suatu organisasi yang mempunyai pegawai dari latar belakang pendidikan,
maka populasi pegawai itu berstrata.

111. Teknik sampling - Probability Sampling
C. Disproportionate Stratified Random Sampling
• Teknik ini digunakan untuk menentukan jumlah sampel, bila populasi
berstrata tetapi kurang proporsional.
• Misalnya, pegawai PT. X: S3: 3 orang, S2: 4, S1: 90, SMU 800, SMP 700,
maka 3 orang lulusan S3 dan 4 orang S2 diambil semua sebagai sampel.
Karena dua kelompok terlalu kecil bila dibanding dengan kelompok S1,
SMU, dan SMP.
d. Cluster Sampling (Area Sampling)
• Teknik sampling untuk menentukan sampel bila obyek yang akan diteliti
atau sumber data sangat luas.
• Misal penduduk dari suatu negara, propinsi atau kabupaten. Untuk
menentukan penduduk mana yang akan dijadikan sumber data,
pengambilan sampel berdasarkan daerah populasi yang ditetapkan.

112. Teknik sampling - Nonprobability Sampling
2. Nonprobability Sampling
• Nonprabability Sampling adalah teknik yang tidak memberi
peluang/kesempatan sama bagi setiap unsur atau anggota
populasi untuk dipilih menjadi sampel.
a. Sampling Sistematis
• Sampling Sistematis adalah teknik penentuan sampel
berdasarkan urutan dari anggota populasi yang telah diberi
nomor urut.
• Misalnya anggota populasi yang terdiri dari 100 orang.
– Dari semua anggota itu diberi nomor urut, yaitu nomor 1
sampai dengan nomor 100. Pengambilan sampel dapat
dilakukan dengan nomor ganjil saja, genap saja, atau
kelipatan dari bilangan tertentu, misalnya kelipatan dari
bilangan lima. Untuk ini maka yang diambil sebagai sampel
adalah nomor 5, 10, 15, 20, dan seterusnya sampai 100.

113. Teknik sampling - Nonprobability Sampling
b. Sampling Kuota
• Sampling Kuota adalah teknik untuk menentukan sampel dari
populasi yang mempunyai ciri-ciri tertentu sampai jumlah
(kuota) yang diiginkan.
• Sebagai contoh, akan melakukan penelitian terhadap pegawai
golongan II, dan penelitian dilakukan secara kelompok.
– Setelah jumlah sampel ditentukan 100, dan jumlah
anggota peneiiti berjumlah 5 orang, maka setiap anggota
peneliti dapat memilih sampel secara bebas sesuai dengan
karateristik yang ditentukan (golongan II) sebanyak 20
orang.
c. Sampling Aksidental
• Sampling Aksidental adalah teknik penentuan sampel
berdasarkan kebetulan, yaitu siapa saja yang secara
kebetulan bertemu dengan peneliti dapat digunakan sebagai
sampel, bila dipandang orang yang kebetulan ditemui itu
cocok sebagai sumber data.

114. Teknik sampling - Nonprobability Sampling
d. Sampling Purposive
• Sampling Purposive adalah teknik penentuan sampel
dengan pertimbangan tertentu. Misalnya akan
melakukan penelitian tentang disiplin pegawai, maka
sampel yang dipilih adalah orang yang ahli dalam
bidang kepegawaian saja.
e. Sampling Jenuh
• Sampling Jenuh adalah teknik penentuan sampel bila
semua anggota populasi digunakan sebagai sampel.
Hal ini sering dilakukan bila jumlah populasi relatif
kecil, kurang dari 30 orang. Istilah lain sampel jenuh
adalah sensus, dimana semua anggota populasi
dijadikan sampel.

115. Teknik sampling - Nonprobability Sampling
f. Snowball Sampling
• Snowball sampling adalah teknik penentuan sampel yang mula-mula
jumlahnya kecil, kemudian sampel ini disuruh memilih teman-temannya
untuk dijadikan sampel. Begitu seterusnya, sehingga jumlah sampel
semakin banyak. Ibarat bola salju yang menggelinding, makin lama
semakin besar. Pada penelitian kualitatif banyak menggunakan sampel
Purposive dan Snowball.

116. Cara Melakukan Teknik Sampling
• Beberapa kriteria yang perlu diperhatikan dalam mengambil sampel
adalah sebagai berikut:
– Tentukan dulu daerah generalisasinya.
– Berilah batas-batas yang tegas tentang sifat-sifat populasi.
– Tentukan sumber-sumber informasi tentang populasi.
– Pilihlah teknik sampling dan hitunglah besar anggota sampel yang
sesuai dengan tujuan penelitiannya.
– Rumuskan persoalan yang akan diteliti.
– Tentukan/cari keterangan mengenai populasi yang akan diteliti.
– Definisikan unit-unit, istilah yang diperlukan.
– Tentukan unit sampling yang diperlukan.
– Tentukan skala pengukuran yang akan dipergunakan.
– Cari keterangan yang ada kaitannya dengan permasalahan yang
akan dibahas.
– Tentukan ukuran sampel yang akan dianalisis.

117. Cara melakukan teknik sampling
• Teknik sampling berguna agar:
– Mereduksi anggota populasi menjadi anggota
sampel yang mewakili populasinya (representatif),
sehingga kesimpulan terhadap populasi dapat
dipertanggungjawabkan,
– Lebih teliti menghitung yang sedikit daripada yang
banyak,
– Menghemat waktu, tenaga, biaya, menghemat
benda coba yang merusak.

118. Cara melakukan teknik sampling
• Beberapa kriteria yang perlu diperhatikan dalam mengambil
sampel adalah sebagai berikut:
– Menentukan daerah generalisasinya.
Banyak penelitian menurun mutunya karena generalisasi
kesimpulannya terlalu luas. Penyebabnya ialah karena
peneliti ingin agar hasil penelitiannya berlaku secara
meluas dan menganggap sampel yang dipilihnya sudah
mewakili populasinya.
– Membeikan batas yang tegas tentang sifat-sifat populasi.
Populasi tidak harus manusia. Populasi dapat pula berupa
benda-benda lainnya. Semua benda-benda yang akan
dijadikan populasi harus ditegaskan batas-batas
karakteristiknya, sehingga dapat menghindari kekaburan
dan kebingungan.
– Menentukan sumber-sumber informasi tentang populasi.
Ada beberapa sumber informasi yang dapat memberi
petunjuk tentang karakteristik suatu populasi. Umpamanya
didapat dari dokumen-dokumen.

119. Cara melakukan teknik sampling
• Beberapa kriteria yang perlu diperhatikan dalam mengambil
sampel adalah sebagai berikut:
– Pilih teknik sampling dan hitung besar anggota sampel yang
sesuai dengan tujuan penelitian.
– Rumuskan persoalan yang akan diteliti.
– Tentukan/cari keterangan mengenai populasi yang akan
diteliti.
– Definisikan unit-unit, istilah yang diperlukan.
– Tentukan unit sampling yang diperlukan.
– Tentukan skala pengukuran yang akan dipergunakan.
– Cari keterangan yang ada kaitannya dengan permasalahan
yang akan dibahas.
– Tentukan ukuran sampel yang akan dianalisis.

120. Penentuan besarnya anggota sampel
a. Contoh Menentukan Ukuran Sampel dengan Tabel Krecjie dan
Nomogram Harry King.
– Penelitian akan dilakukan terhadap iklim kerja suatu organisasi.
– Sumber data yang digunakan adalah para pegawai yang ada pada
organisasi tersebut (populasi).
– Jumlah pegawainya 1000 terdiri atas lulusan
• S1 = 50
• SM = 300
• SMK = 500
• SMP = 50
• SD = 100
(populasi berstrata).

121. Penentuan besarnya anggota sampel
• Jumlah populasi = 1000.
• Bila kesalahan 5%, maka jumlah sampelnya = 278.
• Karena populasi berstrata, maka sampelnya juga berstrata.
Stratanya menurut tingkat pendidikan. Dengan demikian
masing-masing sampel untuk tingkat pendidikan harus
proporsional sesuai dengan populasi. Jadi jumlah sampel untuk

122. Penentuan besarnya anggota sampel
• Pada perhitungan yang terdapat koma dibulatkan ke atas
sehingga jumlah sampelnya lebih 278 yaitu 280. Hal ini lebih
aman daripada kurang dari 278.
• Gambaran jumlah populasi dan sampel dapat ditunjukkan pada
gambar berikut

123. Penentuan besarnya anggota sampel
b. Contoh Menentukan Ukuran Sampel dengan Perhitungan
• Bila ukuran sampel lebih dari 100.000, maka peneliti tidak bisa melihat tabel
lagi, oleh karena itu peneliti harus dapat menghitung sendiri.
• Contoh 1:
– Misal seorang peneliti ingin mengetahui produktivitas kerja pegawai di
lembaga A. peneliti berhipotesis bahwa produktivitas kerja pegawai di
lembaga A paling sedikit 70 dari tolok ukur ideal yang ditetapkan. Untuk
menghitung ukuran sampel sebagai sumber datanya diperlukan rumus
sebagai berikut.
– n ≥ pq/ σp
2
– n= Ukuran sampel yang diperlukan
– p= Prosentase hipotesis (Ho) dinyatakan dalam peluang yang besarnya =
0,70
– q= 1 – 0,50 = 0,50
– σp= Perbedaan antara Ha dan Ho, dibagi dengan z pada tingkat
kepercayaan tertentu.

124. Penentuan Besarnya Anggota Sampel
• Untuk tingkat kepercayaan
– 68%, z = 1
– 95%, z = 1,96
– 99%, z = 2,58.
• Misal taraf kepercayaan 95% berarti z = 1,96 maka:
• Dengan demikian maka besamya ukuran sampel yang diperlukan sebagai
sumber data pada taraf kepercayaan 95% adalah:
• Atau 25 orang jadi paling sedikit diperlukan 25 orang sebagai sumber data.

125. Penentuan Besarnya Anggota Sampel
• Contoh 2
• Untuk menaksir berapa tingkat kepuasan kerja pegawai di lembaga
B diperlukan sebuah sampel. Taraf kepercayaan yang dikehendaki
99%. Perbedaan antara yang ditaksir dengan tolok ukur yang
ditetapkan tidak lebih dari 10%. Jika diketahui simpangan bakunya
20% maka ukuran sampel dapat dihitung dengan rumus sebagai
berikut:
• Dimana
• n = Ukuran sampel yang diperlukan
• b = Perbedaan antara yang ditaksir dengan tolok ukur penafsiran
• z = Harganya tergantung pada taraf kepercayaan yang ditetapkan.
(lihat keterangan pada contoh pertama).
• σ = Simpangan baku

126. Penentuan Besarnya Anggota Sampel
• Contoh 2
• Untuk menaksir berapa tingkat kepuasan kerja pegawai di lembaga B
diperlukan sebuah sampel. Taraf kepercayaan yang dikehendaki 99%.
Perbedaan antara yang ditaksir dengan tolok ukur yang ditetapkan
tidak lebih dari 10%. Jika diketahui simpangan bakunya 20% maka
ukuran sampel dapat dihitung dengan rumus sebagai berikut.
• Untuk contoh di atas maka besarnya sampel dapat dihitung.

127. Kesalahan Umum dalam Menentukan Anggota
Sampel
1. Gagal dalam menetapkan jumlah anggota populasi yang dapat
dipercaya
2. Menggunakan anggota sampel yang terlalu kecil.
3. Tidak menggunakan teknik sampling startified yang disyaratkan
4. Mengubah prosedur teknik sampling;
5. Mengubah rumus untuk menghitung besarnya anggota sampel
6. Memilih anggota sampel yang tidak sesuai dengan tujuan penelitian
7. Mengurangi anggota sampel yang telah ditentukan oleh
perhitungannya;
8. Memilih grup eksperimen dan grup kontrol dari populasi yang
berbeda;
9. Peneliti yang memakai grup sukarela, lupa atau sengaja tidak
membedakannya dengan grup wajib, akibatnya peneliti gagal dalam
menginterpretasikan hasil penelitiannya;

128. Kesalahan umum dalam menentukan anggota
sampel
10. Tidak memberikan alasan-alasan mengapa rumus dan
teknik sampling tertentu yang ia gunakan di dalam
penelitian.
11. Pemeriksaan yang kurang teliti dan lengkap terhadap
populasi
12. Kekeliruan nonsampling, penyebabnya adalah:
a) Populasi tidak didefinisikan sebagaimana mestinya.
b) Penyimpangan populasi tidak dipelajari.
c) Kuesioner tidak dirancang sesuai dengan keperluan.
d) Rumusan dan istilah tidak dipergunakan sebagaimana
mestinya.
e) Peneliti kurang memahami isi dari kuesioner sehingga
jawaban responden kurang sesuai dengan keinginan.
f) Responden tidak memberikan jawaban yang objektif
untuk memberikan jawaban.

129. 129
SEKIAN DAN
TERIMA
KASIH

130. TABEL NORMAL Z
0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09
0.0 0.0000 0.0040 0.0080 0.0120 0.0160 0.0199 0.0239 0.0279 0.0319 0.0359
0.1 0.0398 0.0438 0.0478 0.0517 0.0557 0.0596 0.0636 0.0675 0.0714 0.0753
0.2 0.0793 0.0832 0.0871 0.0910 0.0948 0.0987 0.1026 0.1064 0.1103 0.1141
0.3 0.1179 0.1217 0.1255 0.1293 0.1331 0.1368 0.1406 0.1443 0.1480 0.1517
0.4 0.1554 0.1591 0.1628 0.1664 0.1700 0.1736 0.1772 0.1808 0.1844 0.1879
0.5 0.1915 0.1950 0.1985 0.2019 0.2054 0.2088 0.2123 0.2157 0.2190 0.2224
0.6 0.2257 0.2291 0.2324 0.2357 0.2389 0.2422 0.2454 0.2486 0.2517 0.2549
0.7 0.2580 0.2611 0.2642 0.2673 0.2704 0.2734 0.2764 0.2794 0.2823 0.2852
0.8 0.2881 0.2910 0.2939 0.2967 0.2995 0.3023 0.3051 0.3078 0.3106 0.3133
0.9 0.3159 0.3186 0.3212 0.3238 0.3264 0.3289 0.3315 0.3340 0.3365 0.3389
1.0 0.3413 0.3438 0.3461 0.3485 0.3508 0.3531 0.3554 0.3577 0.3599 0.3621
1.1 0.3643 0.3665 0.3686 0.3708 0.3729 0.3749 0.3770 0.3790 0.3810 0.3830
1.2 0.3849 0.3869 0.3888 0.3907 0.3925 0.3944 0.3962 0.3980 0.3997 0.4015
1.3 0.4032 0.4049 0.4066 0.4082 0.4099 0.4115 0.4131 0.4147 0.4162 0.4177
1.4 0.4192 0.4207 0.4222 0.4236 0.4251 0.4265 0.4279 0.4292 0.4306 0.4319
1.5 0.4332 0.4345 0.4357 0.4370 0.4382 0.4394 0.4406 0.4418 0.4429 0.4441

131. TABEL NORMAL Z
0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09
1.6 0.4452 0.4463 0.4474 0.4484 0.4495 0.4505 0.4515 0.4525 0.4535 0.4545
1.7 0.4554 0.4564 0.4573 0.4582 0.4591 0.4599 0.4608 0.4616 0.4625 0.4633
1.8 0.4641 0.4649 0.4656 0.4664 0.4671 0.4678 0.4686 0.4693 0.4699 0.4706
1.9 0.4713 0.4719 0.4726 0.4732 0.4738 0.4744 0.4750 0.4756 0.4761 0.4767
2.0 0.4772 0.4778 0.4783 0.4788 0.4793 0.4798 0.4803 0.4808 0.4812 0.4817
2.1 0.4821 0.4826 0.4830 0.4834 0.4838 0.4842 0.4846 0.4850 0.4854 0.4857
2.2 0.4861 0.4864 0.4868 0.4871 0.4875 0.4878 0.4881 0.4884 0.4887 0.4890
2.3 0.4893 0.4896 0.4898 0.4901 0.4904 0.4906 0.4909 0.4911 0.4913 0.4916
2.4 0.4918 0.4920 0.4922 0.4925 0.4927 0.4929 0.4931 0.4932 0.4934 0.4936
2.5 0.4938 0.4940 0.4941 0.4943 0.4945 0.4946 0.4948 0.4949 0.4951 0.4952
2.6 0.4953 0.4955 0.4956 0.4957 0.4959 0.4960 0.4961 0.4962 0.4963 0.4964
2.7 0.4965 0.4966 0.4967 0.4968 0.4969 0.4970 0.4971 0.4972 0.4973 0.4974
2.8 0.4974 0.4975 0.4976 0.4977 0.4977 0.4978 0.4979 0.4979 0.4980 0.4981
2.9 0.4981 0.4982 0.4982 0.4983 0.4984 0.4984 0.4985 0.4985 0.4986 0.4986
3.0 0.4987 0.4987 0.4987 0.4988 0.4988 0.4989 0.4989 0.4989 0.4990 0.4990

132. Tabel t-Student
dfp 0.40 0.25 0.10 0.05 0.025 0.01 0.005 0.0005
1 0.324920 1.000000 3.077684 6.313752 12.70620 31.82052 63.65674 636.6192
2 0.288675 0.816497 1.885618 2.919986 4.30265 6.96456 9.92484 31.5991
3 0.276671 0.764892 1.637744 2.353363 3.18245 4.54070 5.84091 12.9240
4 0.270722 0.740697 1.533206 2.131847 2.77645 3.74695 4.60409 8.6103
5 0.267181 0.726687 1.475884 2.015048 2.57058 3.36493 4.03214 6.8688
6 0.264835 0.717558 1.439756 1.943180 2.44691 3.14267 3.70743 5.9588
7 0.263167 0.711142 1.414924 1.894579 2.36462 2.99795 3.49948 5.4079
8 0.261921 0.706387 1.396815 1.859548 2.30600 2.89646 3.35539 5.0413
9 0.260955 0.702722 1.383029 1.833113 2.26216 2.82144 3.24984 4.7809
10 0.260185 0.699812 1.372184 1.812461 2.22814 2.76377 3.16927 4.5869
11 0.259556 0.697445 1.363430 1.795885 2.20099 2.71808 3.10581 4.4370
12 0.259033 0.695483 1.356217 1.782288 2.17881 2.68100 3.05454 4.3178
13 0.258591 0.693829 1.350171 1.770933 2.16037 2.65031 3.01228 4.2208
14 0.258213 0.692417 1.345030 1.761310 2.14479 2.62449 2.97684 4.1405

133. Tabel t-Student
dfp 0.40 0.25 0.10 0.05 0.025 0.01 0.005 0.0005
15 0.257885 0.691197 1.340606 1.753050 2.13145 2.60248 2.94671 4.0728
16 0.257599 0.690132 1.336757 1.745884 2.11991 2.58349 2.92078 4.0150
17 0.257347 0.689195 1.333379 1.739607 2.10982 2.56693 2.89823 3.9651
18 0.257123 0.688364 1.330391 1.734064 2.10092 2.55238 2.87844 3.9216
19 0.256923 0.687621 1.327728 1.729133 2.09302 2.53948 2.86093 3.8834
20 0.256743 0.686954 1.325341 1.724718 2.08596 2.52798 2.84534 3.8495
21 0.256580 0.686352 1.323188 1.720743 2.07961 2.51765 2.83136 3.8193
22 0.256432 0.685805 1.321237 1.717144 2.07387 2.50832 2.81876 3.7921
23 0.256297 0.685306 1.319460 1.713872 2.06866 2.49987 2.80734 3.7676
24 0.256173 0.684850 1.317836 1.710882 2.06390 2.49216 2.79694 3.7454
25 0.256060 0.684430 1.316345 1.708141 2.05954 2.48511 2.78744 3.7251
26 0.255955 0.684043 1.314972 1.705618 2.05553 2.47863 2.77871 3.7066
27 0.255858 0.683685 1.313703 1.703288 2.05183 2.47266 2.77068 3.6896
28 0.255768 0.683353 1.312527 1.701131 2.04841 2.46714 2.76326 3.6739
29 0.255684 0.683044 1.311434 1.699127 2.04523 2.46202 2.75639 3.6594
30 0.255605 0.682756 1.310415 1.697261 2.04227 2.45726 2.75000 3.6460
inf 0.253347 0.674490 1.281552 1.644854 1.95996 2.32635 2.57583 3.2905