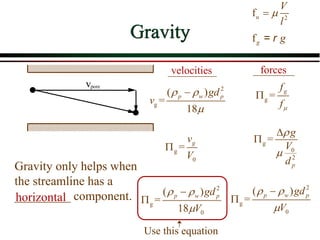
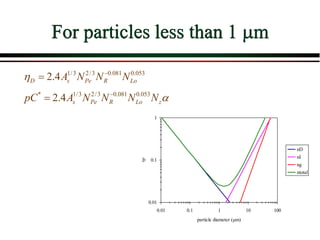
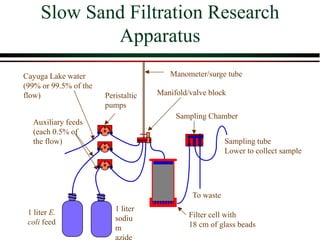
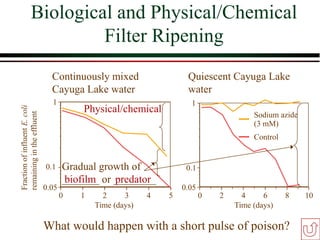
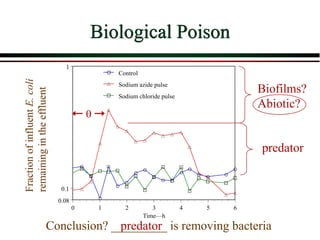
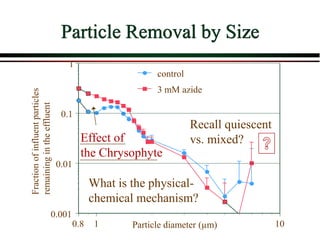
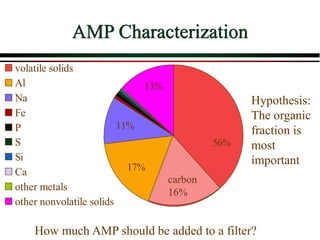
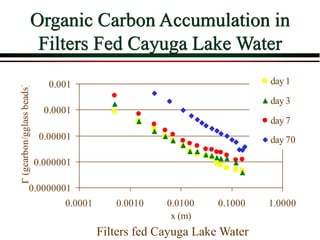
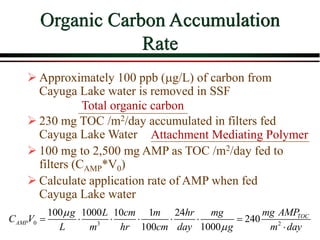
The document summarizes information from public health reports on the decline of typhoid fever in the late 19th/early 20th century. It finds that: 1) The decline happened gradually over time and was not associated with any centralized intervention like water filtration or chlorination. 2) Improved personal hygiene was likely the dominant factor in reducing typhoid, as the disease spread through food preparation with contaminated hands rather than centralized systems like water or milk. 3) Other factors like refrigeration and commercial/home refrigeration may have reduced summertime increases in typhoid by limiting bacterial growth in food.

1. Monroe L. Weber-Shirk
School of Civil and
Environmental Engineering
Filtration Theory

2. Field Trip To CUWTP
Monday at
2:20 pm at
loading dock

3. Public Health reports
 The decline happened over time and not rapidly as if it were associated with a
centralized intervention
 Chlorine was not responsible for the decline
 Filtration was not responsible for the decline
 The relatively high dose required for an infection would require gross
contamination of the water supply
 Therefore typhoid was generally not waterborne
 There is some evidence that typhoid was greater in the summer. This suggests
multiplication in the environment, most likely in food.
 Improved personal hygiene was likely the dominant factor
 Jakarta and Army evidence that the sources are local: (not centrally distributed like
milk, water, or meat, but food preparation with contaminated hands)
 Improved hygiene reduced contamination of food
 Refrigeration would have reduced the summertime typhoid by reducing
multiplication in food. Home refrigeration happened after the decline began, but
commercial refrigeration

4. Filtration Outline
 Particle Capture theory
Transport
Short range forces
Grain contact points
Dimensional Analysis
Trajectory Models
 Filters
Rapid
Slow (lots of detail here…)

5. References
 Tufenkji, N. and M. Elimelech (2004). "Correlation equation for
predicting single-collector efficiency in physicochemical filtration in
saturated porous media." Environmental-Science-and-Technology
38(2): 529-536.
 Cushing, R. S. and D. F. Lawler (1998). "Depth Filtration:
Fundamental Investigation through Three-Dimensional Trajectory
Analysis." Environmental Science and Technology 32(23): 3793 -
3801.
 Tobiason, J. E. and C. R. O'Melia (1988). "Physicochemical Aspects of
Particle Removal in Depth Filtration." Journal American Water Works
Association 80(12): 54-64.
 Yao, K.-M., M. T. Habibian, et al. (1971). "Water and Waste Water
Filtration: Concepts and Applications." Environmental Science and
Technology 5(11): 1105.

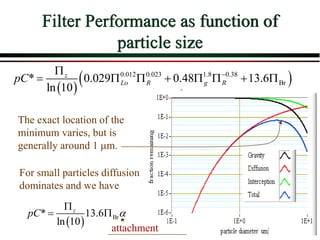
6. Overall Filter Performance
Iwasaki (1937) developed relationships
describing the performance of deep bed
filters.
0
=
dC
C
dz


C is the particle concentration [number/L3]
0 is the initial filter coefficient [1/L]
z is the media depth [L]
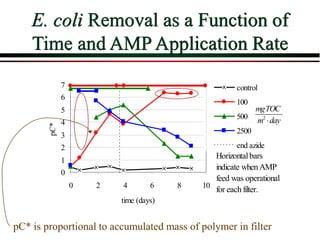
The particle’s chances of being caught are the same at all
depths in the filter; pC* is proportional to depth
0
=
dC
dz
C


0
0
0
=
C z
C
dC
dz
C


  0
0
ln =
C
z
C

 
  
 
  0
0
1
log *
ln 10
C
pC z
C

 
  
 
 

7. Particle Removal Mechanisms in
Filters
Transport to a surface
Attachment
Molecular diffusion
Inertia
Gravity
Interception
Straining
London van der Waals
collector

8. Filtration Performance: Dimensional
Analysis
What is the parameter we are interested in
measuring? _________________
How could we make performance
dimensionless? ____________
What are the important forces?
Effluent concentration
C/C0 or pC*
Inertia London van der Waals Electrostatic
Viscous
Need to create dimensionless force ratios!
Gravitational Thermal

9. Dimensionless Force Ratios
Reynolds Number
Froude Number
Weber Number
Mach Number
Pressure/Drag Coefficients
(dependent parameters that we measure experimentally)
Re
Vl
r
m
=
Fr
V
gl
=
( )
2
2
Cp
p
V
r
- D
=


l
V
W
2

c
V
M 
A
V
d
2
Drag
2
C


2
fu
V
l
m
=
fg g
r
=
2
f
l
s
s
=
2
f v
E
c
l
r
=
2
fi
V
l
r
=
( )
p g z
r
D + D

10. What is the Reynolds number for
filtration flow?
 What are the possible length scales?
 Void size (collector size) max of 0.7 mm in RSF
 Particle size
 Velocities
 V0 varies between 0.1 m/hr (SSF) and 10 m/hr (RSF)
 Take the largest length scale and highest velocity to find max
Re
 Thus viscosity is generally much more significant than inertia
 
3
3
1000 10 0.7 10
3600
Re 2
0.001
kg m hr
m
m hr s
kg
m s

  

  
  
 
 
 

 
Re
Vl




11. Choose viscosity!
In Fluid Mechanics inertia is a significant
“force” for most problems
In porous media filtration viscosity is more
important that inertia.
We will use viscosity as the repeating
parameter and get a different set of
dimensionless force ratios
Inertia
London
Viscous
Gravitational
Viscous
Thermal
Viscous
Electrostatic
Viscous

12. Gravity
2
g
0
( )
=
18
p w p
gd
V
 



2
g
( )
=
18
p w p
gd
v
 


vpore
g
0
=
g
v
V

Gravity only helps when
the streamline has a
_________ component.
horizontal
2
fu
V
l


fg g
r
=
g =
g
f
f

g
0
2
=
p
g
V
d




2
g
0
( )
= p w p
gd
V
 



velocities forces
Use this equation

13. Diffusion (Brownian Motion)
kB=1.38 x 10-23 J/°K
T = absolute temperature
vpore
2/3
2/3
-2/3 0
Br
0
=
3
c B
p c
V d k T
Pe
D d V d



 
 
   
   
   
3
B
p
k T
D
d


2
L
T
 
 
 
0 c
V d
Pe
D

d
c
D
v
d

dc is diameter of the collector
Diffusion velocity is
high when the particle
diameter is ________.
small
The exponent was obtained from an analytical model

14. London van der Waals
The London Group is a measure of the
attractive force
H is the Hamaker’s constant

Lo 2
p 0
4H
=
9 d V


20
= 0.75 10
H J


Van der Waals force
Viscous force

15. What about Electrostatic?
 Modelers have not succeeded in describing filter
performance when electrostatic repulsion is
significant
 Models tend to predict no particle removal if
electrostatic repulsion is significant.
 So until we get a better model we will neglect this
force with the understanding that filter
performance is poor if electrostatic repulsion is
significant

16. Geometric Parameters
What are the length scales that are related to
particle capture by a filter?
______________
__________________________
______________
Create dimensionless groups
Choose the repeating length ________
Filter depth (z)
Collector diameter (media size) (dc)
Particle diameter (dp)
p
R
c
d
d
  z
c
z
d
 
(dc)
Number of collectors!

17. Write the functional relationship
 
, ,
g Br Lo
* , ,
R z
pC f
     
 
, ,
g Br Lo
* ,
z R
pC f
     
If we double depth of filter what does pfz do? ___________
doubles
How do we get more detail on this functional relationship?
Empirical measurements
Numerical models

18. Numerical Models
Trajectory analysis (similar to the analysis
of flocculation)
A series of modeling attempts with
refinements
Began with a “single collector” model that
modeled London and electrostatic forces
with an attachment efficiency term (a)
 
, ,
g Br Lo
* ,
z R
pC f
       
 
g Br
*
ln 10
z
R
pC a


    
Addition
assumption

19. Array of Spheres Model (AOS)
Includes simplified geometry describing the
contact between collectors
Used trajectory analysis to determine which
particles would be captured
Used the numerical model results to
determine the form of the equation based on
dimensional analysis

20. AOS: The Media Trap
Isolated collectors Array of spheres model
Collector
Contacts

21. Contacts Matter!
Two Particle Traps
Particles that enter
centered above a
collector are trapped
in the stagnation
point.
Particles that enter on a
streamline that passes
through a contact point
between collectors get
trapped between two
collectors
This trajectory
analysis ignores
Brownian Motion
Collector
contact straining
 
 
0.012 0.023 1.8 0.38
* 0.029 0.48
ln 10
z
Lo R g R
pC 

     

22. Array of Spheres Model Results and
Critique
 
 
0.012 0.023 1.8 0.38
Br
* 0.029 0.48 13.6
ln 10
z
Lo R g R
pC 

       
Brownian wasn’t modeled
 The transport to the media surface by either the
fluid (interception, R), gravity (g), or diffusion
(Br) is followed by an attachment step controlled
by van der Waals (Lo)
 The transport and attachment steps occur in series
and thus removal should be described by the
product of these groups
 More work to be done!
13.6=4.04*As
1/3

23. AOS model deficiencies
 
 
0.012 0.023 1.8 0.38
Br
* 0.029 0.48 13.6
ln 10
z
Lo R g R
pC 

       
 
 
1.8 0.38
Br
* 0.029 0.48 13.6
ln 10
z
g R
pC 

     
=1!
This suggests a third transport mechanisms that is
constant and doesn’t require Brownian motion or
sedimentation! Could be interception, but interception
increases with particle size.
Given this error (and the likelihood that the numerical
model contained errors) the model results from the AOS
model should probably not be used!

24. Tufenkji and Elimelech with
Analysis by Weber-Shirk
vdW
H
=
N
kT
Pe
0 0
3
B
c p c
k T
D
N
V d d V d

 
 
   
   
   
2
G
0
( )
=
18
p p w
d g
N
V
 


p
R
c
d
N
d

0 D I G
   
  
1/3 0.081 0.715 0.052
2.4
D s R Pe vdW
A N N N
 

 
5
5 6
2 1
2 3 3 2
s
A

  


  
 
1/3
1
 
 
vdW
Pe 0
H
=
3
Lo
p c
N
N
N d V d


1/3 0.081 0.715 0.052 0.052
2.4
D s R Pe Pe Lo
A N N N N
  

1/3 2/3 0.081 0.052
2.4
D s Pe R Lo
A N N N
 

Lo 2
p 0
4H
=
9 d
N
V

Note that my NPe is the inverse of T&E

25. Interception
1.55 0.125 0.125
0.55
I S R Pe vdW
A N N N
 
1.55 0.125
0.55
I S R Lo
A N N
 
Pe vdW
0
A
=
3
Lo
p c
N N N
d V d



26. Gravity
0.24 1.11 0.053
0.22
G R G vdW
N N N
 

Pe vdW
0
H
=
3
Lo
p c
N N N
d V d


0.24 1.11 0.053 0.053
0.22
G R G Lo Pe
N N N N
  
 vdW
Pe
Lo
N
N
N


27. Total removal
0 D I G
   
  
1/3 2/3 0.081 0.052
2.4
D s Pe R Lo
A N N N
 

1.55 0.125
0.55
I S R Lo
A N N
 
0.24 1.11 0.053 0.053
0.22
G R G Lo Pe
N N N N
  

1/3 2/3 0.081 0.052 1.55 0.125 0.24 1.11 0.053 0.053
0 2.4 0.55 0.22
s Pe R Lo S R Lo R G Lo Pe
A N N N A N N N N N N
   
  
 
1/3 2/3 0.081 1.55 0.072 0.24 1.11 0.053 0.053
0 2.4 0.55 0.22
s Pe R S R Lo R G Pe Lo
A N N A N N N N N N
   
  

28. 0
ln =
C
z
C

 
  
 
0
3 1
2 c
d

 a


 
1/3 2/3 0.081 1.55 0.072 0.24 1.11 0.053 0.053
0 2.4 0.55 0.22
s Pe R S R Lo R G Pe Lo
A N N A N N N N N N
   
  
 
*
0
1
log
ln 10
C
pC z
C

 
  
 
 
 
 
*
0
3 1
2ln 10 c
z
pC
d

a
  
  
   
 
3 1
2ln 10
z
c
z
N
d

  
  
 
*
0
z
pC N a


29. For particles less than 1 m
1/3 2/3 0.081 0.053
2.4
D s Pe R Lo
A N N N
 

0.01
0.1
1
0.01 0.1 1 10 100
particle diameter (m)

0
nD
nI
ng
ntotal
* 1/3 2/3 0.081 0.053
2.4 s Pe R Lo z
pC A N N N N a



30. Brownian Motion
 Brownian motion dominates the transport and collection of
particles on the order of 1 m and smaller
 Brownian transport (diffusion) leads to nondeterministic
behavior and results in trajectories defined by stochastic
differential equations
 The problem is traditionally decoupled using the
assumption that the Brownian and deterministic transport
mechanisms are additive
 Sedimentation is less important for small particles because
the R group is small and the Br group is large
 
 
0.012 0.023 1.8 0.38
Br
* 0.029 0.48 13.6
ln 10
z
Lo R g R
pC 

       

31. Filter Performance as function of
particle size
The exact location of the
minimum varies, but is
generally around 1 m.
For small particles diffusion
dominates and we have
  Br
* 13.6
ln 10
z
pC a

 
 
 
0.012 0.023 1.8 0.38
Br
* 0.029 0.48 13.6
ln 10
z
Lo R g R
pC 

       
attachment

32. Estimate Dimensionless Brownian
Transport for a Bacteria Cell
 viscosity 1.00E-03 Ns/m2
dp Particle diameter 1.00E-06 m
kB Boltzman constant 1.38E-23 J/°K
dc Collector diameter 0.2E-03 m
T Absolute temperature 293 °K
V0 Filter approach
velocity
0.1 m/hr
Advection is 40x greater than diffusion
2/3
Br
0
13.6 = 13.6
3
B
p c
k T
d V d

 
  
 
 
 
   
2/3
23
Br
3 6 3
2
1.38 10 293
13.6 = 13.6
N s
3 1 10 1 10 0.10 0.2 10
m 3600
J
K
K
m hr
m m
hr s


  
 
 
 
 
 

 
 


   
 
  
   
 
   
 
Br
13.6 = 0.025


33. The Diffusion Surprise
 As particle size
decreases Brownian
motion becomes more
effective
 Viruses should be
removed efficiently by
filters (if attachment is
effective)
2/3
Br
0
13.6 = 13.6
3
B
p c
k T
d V d

 
  
 
 
0.001
0.01
0.1
1
10
1.E-09 1.E-08 1.E-07 1.E-06 1.E-05
Particle diameter (m)
Br
13.6

34. How deep must a filter (SSF) be for
diffusion to remove 99% of bacteria?
 Assume a is 1 and dc
is 0.2 mm
 a is ____
 pfz is ____
 z is _____
 What does this mean?
3.7 cm
1
2
  Br
* 13.6
ln 10
z
pC a

 
 
Br
ln 10 *
13.6
z
c
pC
z
d a
  

 
Br
ln 10 *
13.6
c
pC d
z
a


   
  
3
ln 10 2 0.2 10
0.025 1
m
z



If the attachment efficiency
were 1, then we could get great
particle capture in a 1 m deep
filter!

35. Filtration Technologies
 Slow (Filters→English→Slow sand→Biosand)
First filters used for municipal water treatment
Were unable to treat the turbid waters of the Ohio and
Mississippi Rivers
 Rapid (Mechanical→American→Rapid sand)
Used in Conventional Water Treatment Facilities
Used after coagulation/flocculation/sedimentation
High flow rates→clog daily→hydraulic cleaning
 Ceramic

36. Rapid Sand Filter
(Conventional US Treatment)
Sand
Gravel
Influent
Drain
Effluent Wash water
Anthracite
Size
(mm)
0.70
0.45 - 0.55
5 - 60
Specific
Gravity
1.6
2.65
2.65
Depth
(cm)
30
45
45

37. Filter Design
 Filter media
silica sand and anthracite coal
non-uniform media will stratify with _______ particles
at the top
 Flow rates
2.5 - 10 m/hr
 Backwash rates
set to obtain a bed porosity of 0.65 to 0.70
typically 50 m/hr
smaller

38. Sand
Gravel
Influent
Drain
Effluent Wash water
Anthracite
Backwash
Wash water is
treated water!
WHY?
Only clean water
should ever be on
bottom of filter!

39. Slow Sand Filtration
First filters to be used on a widespread basis
Fine sand with an effective size of 0.2 mm
Low flow rates (10 - 40 cm/hr)
Schmutzdecke (_____ ____) forms on top
of the filter
causes high head loss
must be removed periodically
Used without coagulation/flocculation!
filter cake

40. Typical Performance of SSF Fed
Cayuga Lake Water
0.05
0.1
1
0 1 2 3 4 5
Time (days)
Fraction
of
influent
E.
coli
remaining
in
the
effluent
Filter performance doesn’t improve if the filter
only receives distilled water
(Daily samples)

41. How do Slow Sand Filters
Remove Particles?
 How do slow sand filters remove particles
including bacteria, Giardia cysts, and
Cryptosporidium oocysts from water?
 Why does filter performance improve with time?
 Why don’t SSF always remove Cryptosporidium
oocysts?
 Is it a biological or a physical/chemical
mechanism?
 Would it be possible to improve the performance
of slow sand filters if we understood the
mechanism?

42. Slow Sand Filtration Research
Apparatus
Sampling tube
Lower to collect sample
Manifold/valve block
Peristaltic
pumps
Manometer/surge tube
Cayuga Lake water
(99% or 99.5% of the
flow)
Auxiliary feeds
(each 0.5% of
the flow)
1 liter E.
coli feed
1 liter
sodiu
m
To waste
Filter cell with
18 cm of glass beads
Sampling Chamber

43. Biological and Physical/Chemical
Filter Ripening
0.05
Quiescent Cayuga Lake
water
0.1
1
0 2 4 6 8 10
Time (days)
Control
Sodium azide
(3 mM)
Continuously mixed
Cayuga Lake water
0.05
0.1
1
0 1 2 3 4 5
Time (days)
Fraction
of
influent
E.
coli
remaining
in
the
effluent
What would happen with a short pulse of poison?
Gradual growth of
_______ or ________
biofilm predator
Physical/chemical

44. Biological Poison
Fraction
of
influent
E.
coli
remaining
in
the
effluent
predator
predator
Biofilms?
Abiotic?
Conclusion? _________ is removing bacteria
0.08
0.1
1
0 1 2 3 4 5 6
Time—h
Control
Sodium azide pulse
Sodium chloride pulse
q

45. Chrysophyte
long flagellum used for
locomotion and to provide
feeding current
short flagellum
stalk used to attach to
substrate (not actually
seen in present study)
1 µm

46. Particle Removal by Size
0.001
0.01
0.1
1
0.8 1 10
Particle diameter (µm)
control
3 mM azide
Fraction
of
influent
particles
remaining
in
the
effluent
Effect of
the Chrysophyte
What is the physical-
chemical mechanism?
Recall quiescent
vs. mixed?

47. Role of Natural Particles in SSF
Could be removal by straining
But SSF are removing particles 1 m in
diameter!
To remove such small particles by straining
the pores would have to be close to 1 m
and the head loss would be excessive
Removal must be by attachment to the
sticky particles!

48. Particle Capture Efficiency
Sand filters are inefficient capturers of
particles
Particles come into contact with filter media
surfaces many times, yet it is common for
filters to only remove 90% - 99% of the
particles.
Failure to capture more particles is due to
ineffective __________
Remember the diffusion surprise?
attachment

49. Techniques to Increase Particle
Attachment Efficiency
Make the particles stickier
The technique used in conventional water
treatment plants
Control coagulant dose and other coagulant aids
(cationic polymers)
Make the filter media stickier
Potato starch in rapid sand filters?
Biofilms in slow sand filters?
Mystery sticky agent present in surface waters
that is imported into slow sand filters?

50. Mystery Sticky Agent
Serendipity!
Head loss through a clogged filter decreases
if you add acid
Maybe the sticky agent is acid soluble
Maybe the sticky agent will become sticky
again if the acid is neutralized
Eureka!

51. Cayuga Lake Seston Extract
Concentrate particles from Cayuga Lake
Acidify with 1 N HCl
Centrifuge
Centrate contains polymer
Neutralize to form flocs

52. AMP Characterization
11%
13%
17%
56%
volatile solids
Al
Na
Fe
P
S
Si
Ca
other metals
other nonvolatile solids
How much AMP should be added to a filter?
Hypothesis:
The organic
fraction is
most
important
carbon
16%

53. Organic Carbon Accumulation in
Filters Fed Cayuga Lake Water
0.0000001
0.000001
0.00001
0.0001
0.001
0.0001 0.0010 0.0100 0.1000 1.0000
x (m)
G
(gcarbon/gglass
beads)
day 1
day 3
day 7
day 70
Filters fed Cayuga Lake Water

54. Organic Carbon Accumulation
Rate
 Approximately 100 ppb (g/L) of carbon from
Cayuga Lake water is removed in SSF
 230 mg TOC /m2/day accumulated in filters fed
Cayuga Lake Water
 100 mg to 2,500 mg AMP as TOC /m2/day fed to
filters (CAMP*V0)
 Calculate application rate of AMP when fed
Cayuga Lake water
Total organic carbon
0 3 2
100 1000 10 1 24
240
100 1000
TOC
AMP
mg AMP
g L cm m hr mg
C V
L m hr cm day g m day


      

Attachment Mediating Polymer

55. 0
1
2
3
4
5
6
7
0 2 4 6 8 10
time (days)
pC*
control
100
500
2500
end azide
Horizontalbars
indicate whenAMP
feed was operational
for eachfilter.
2
mgTOC
m day

0
1
2
3
4
5
6
7
0 2 4 6 8 10
time (days)
pC*
control
100
500
2500
end azide
Horizontalbars
indicate whenAMP
feed was operational
for eachfilter.
2
mgTOC
m day

E. coli Removal as a Function of
Time and AMP Application Rate
pC* is proportional to accumulated mass of polymer in filter

56. Head Loss Produced by AMP
0
0.2
0.4
0.6
0.8
1
1.2
0 2 4 6 8 10
time (days)
head
loss
(m)
control
100
500
2500
end azide
2
carbon
mg
m day

How much AMP does it take to get 1 m of head loss?
2 2
500
6 3
carbon carbon
mg g
days
m day m
 


57. What do we know about this
Polymer?
Soluble at very low (<1) and at very high
(>13) pH
Forms flocs readily at neutral pH
Contains protein (amino acids)
In acid solution amino acids are protonated and
exist as cations
In basic solution amino acids are deprotonated
and exist as anions
Could be irrelevant!

58. Dipolar Structure of Amino Acids
H—N —CH—C—O—H
H
R O
..
In acid solution In base solution
H—N —CH—C—O
H
R O
..
H—N —CH—C—O—H
H
R O
H
+
Carboxyl group
Amino group
cation anion

59. Sticky Media vs. Sticky Particles
 Sticky Media
Potentially treat filter
media at the beginning
of each filter run
No need to add
coagulants to water for
low turbidity waters
Filter will capture
particles much more
efficiently
 Sticky Particles
Easier to add coagulant
to water than to coat
the filter media

60. Current and Future Research
 Produce the polymer in the lab with an algae culture
 Develop methods to quantify the polymer
 Develop application techniques to optimize filter
performance
 How can we coat all of the media?
 Will the media remain sticky through a backwash?
 Will it be possible to remove particles from the media with a
normal backwash?
 What are the best ways to use this new coagulant?
 Why does the filter performance deteriorate when the AMP
feed is discontinued?
 Characterize the polymer

61. Conclusions
Filters could remove particles more
efficiently if the _________ efficiency
increased
SSF remove particles by two mechanisms
____________
_____________________________
pC* is proportional to accumulated mass of
AMP in the filter
Predation
Sticky polymer that coats the sand
attachment
 
, ,
g Br Lo
* ,
z R
pC f
      a

62. Contact Points

63. Polymer Accumulation in a Pore