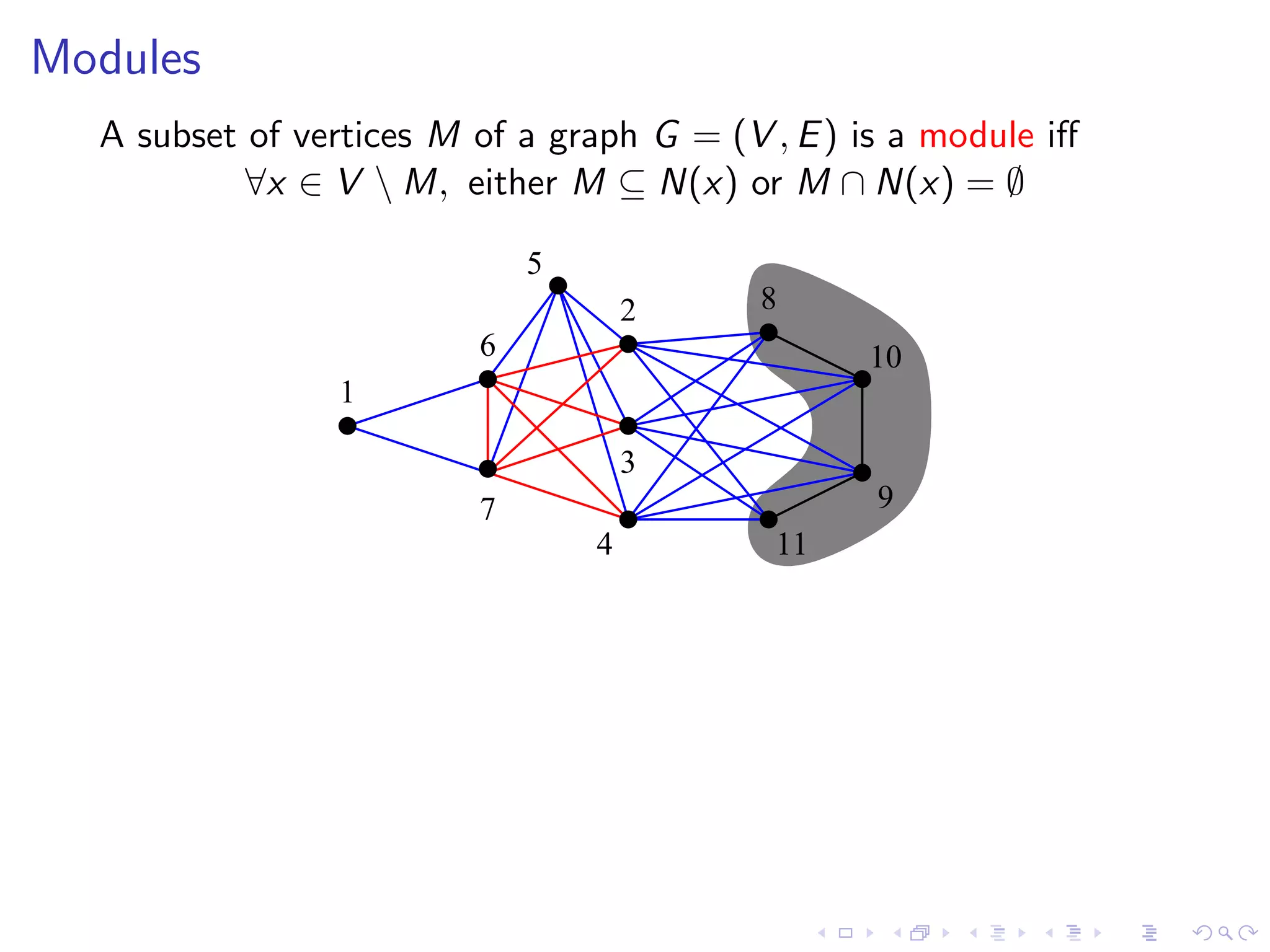
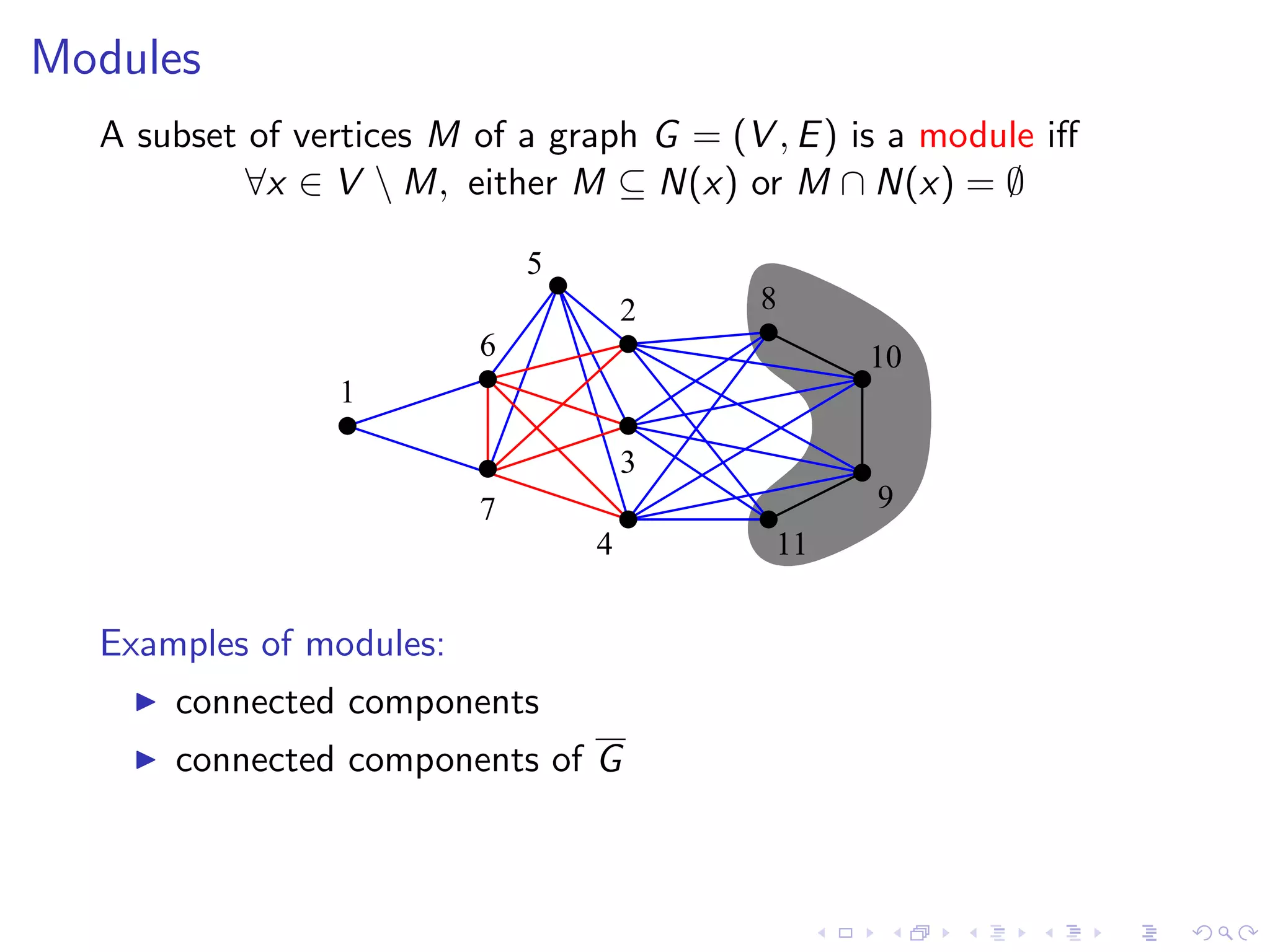
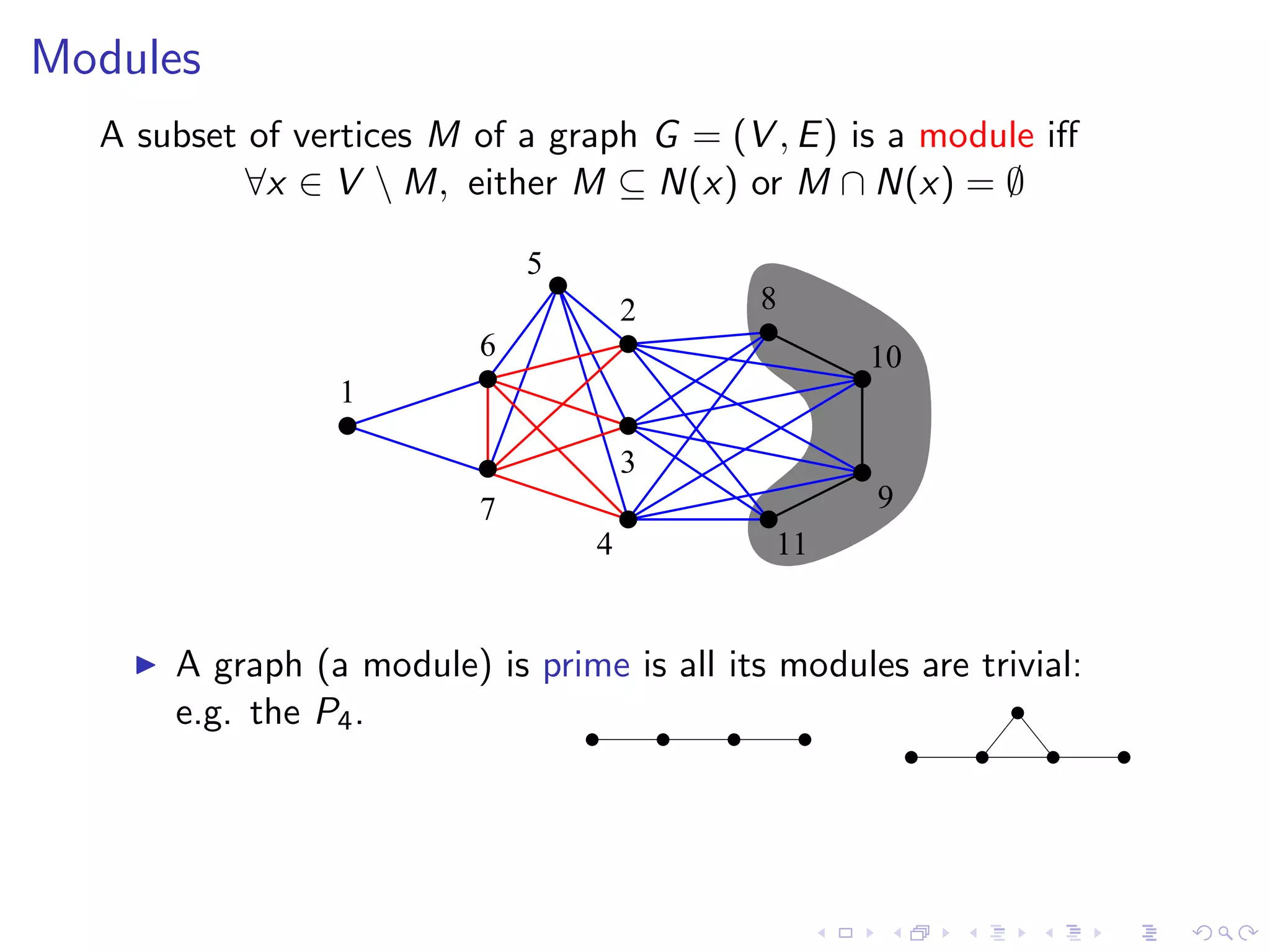
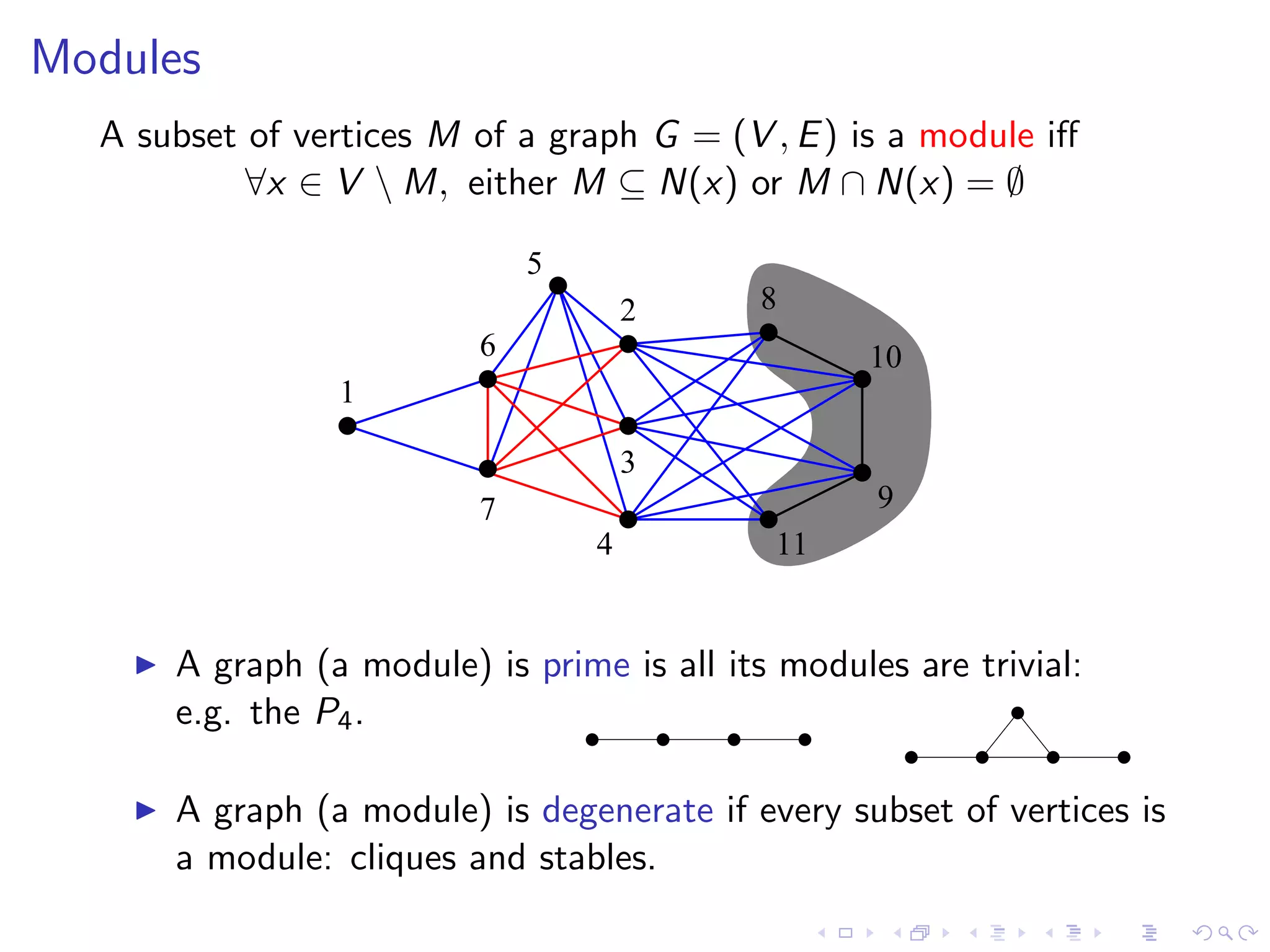
The document summarizes Christophe Paul's work on algorithms for modular decomposition. It discusses Ehrenfeucht et al's modular decomposition algorithm which computes the modular partition M(G,v) of a graph G with respect to a vertex v. It then computes the modular decomposition of the quotient graph G/M(G,v) and the induced subgraphs G[X] for each module X in M(G,v). The document also discusses Gallai's theorem on the decomposition of graphs into parallel, series, or prime modules and algorithms for recognizing cographs and computing the modular decomposition tree.


![Permutation graph recognition
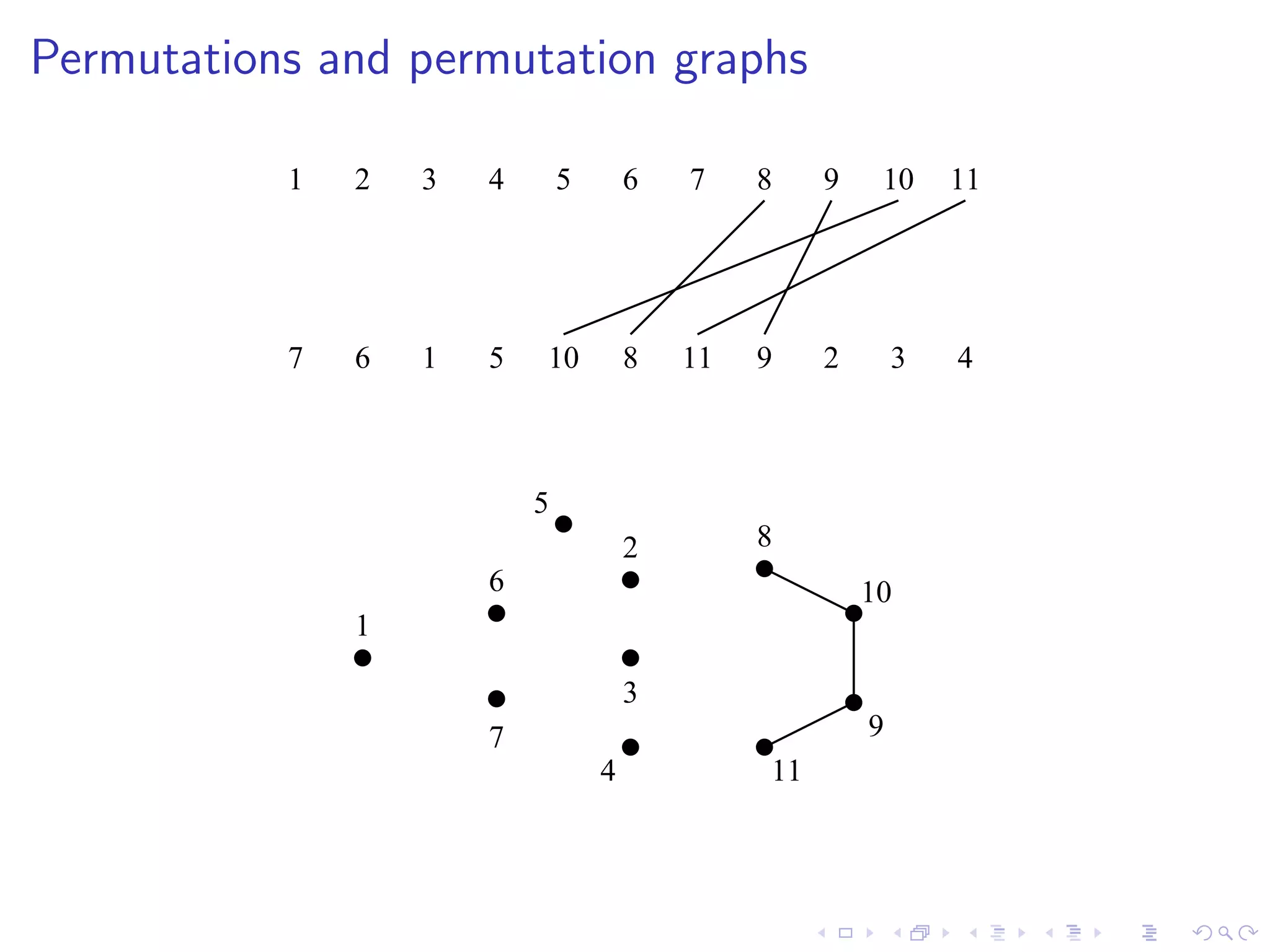
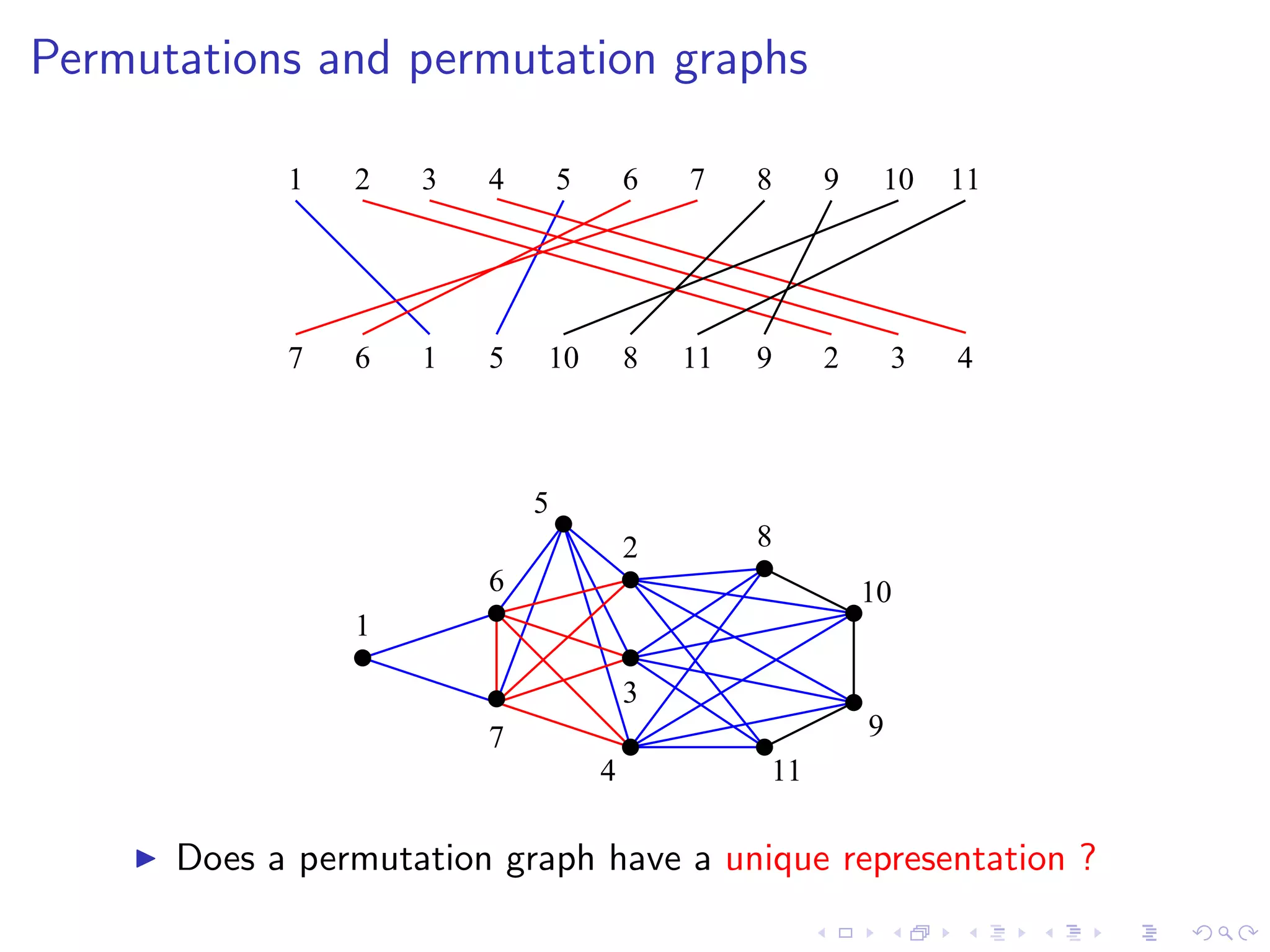
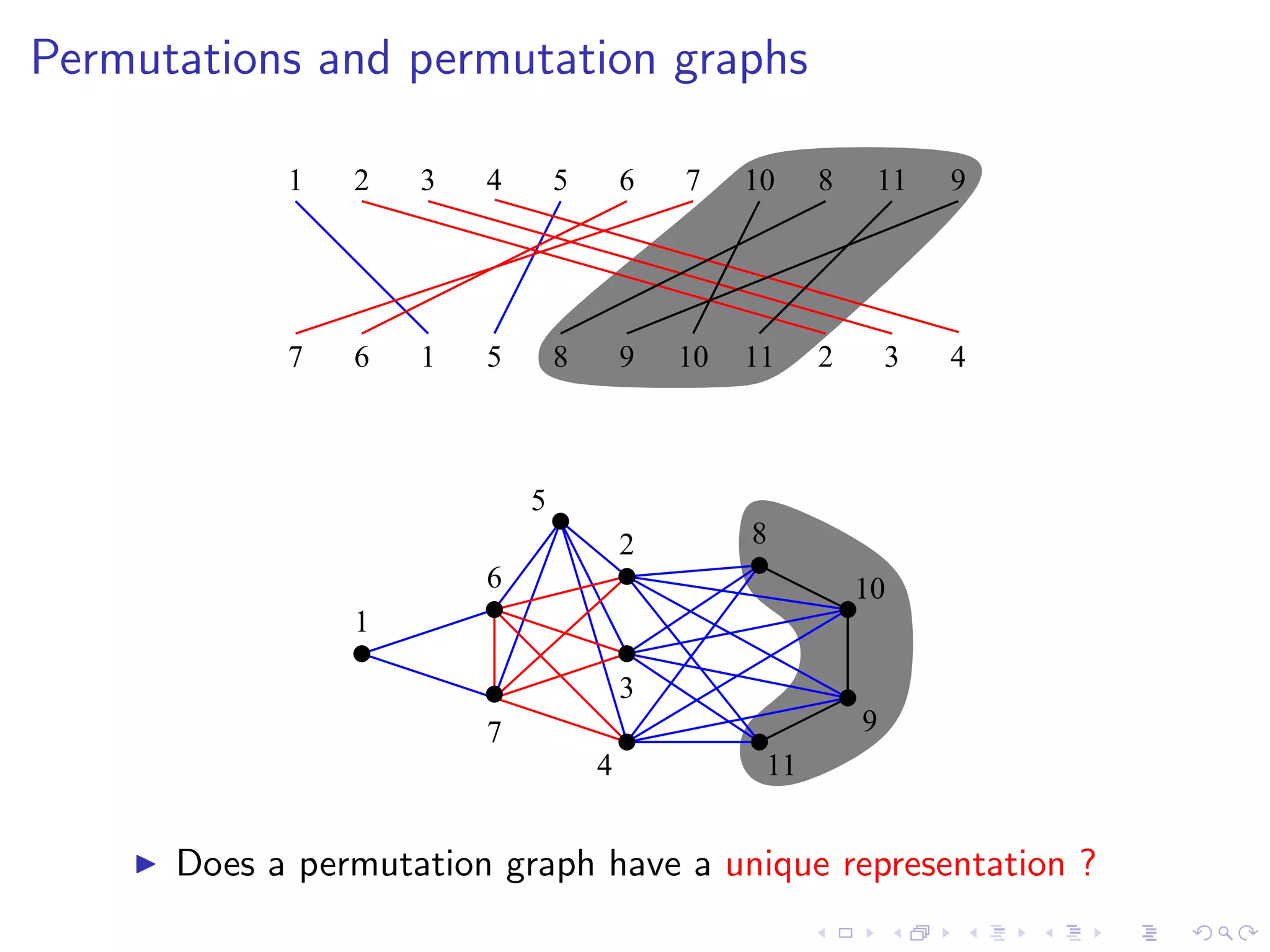
Theorem [Gallai’67]
A permutation graph has a unique representation (up to reversal)
iff it is prime.](https://image.slidesharecdn.com/04paul-120623180515-phpapp01/75/AlgoPerm2012-04-Christophe-Paul-11-2048.jpg)
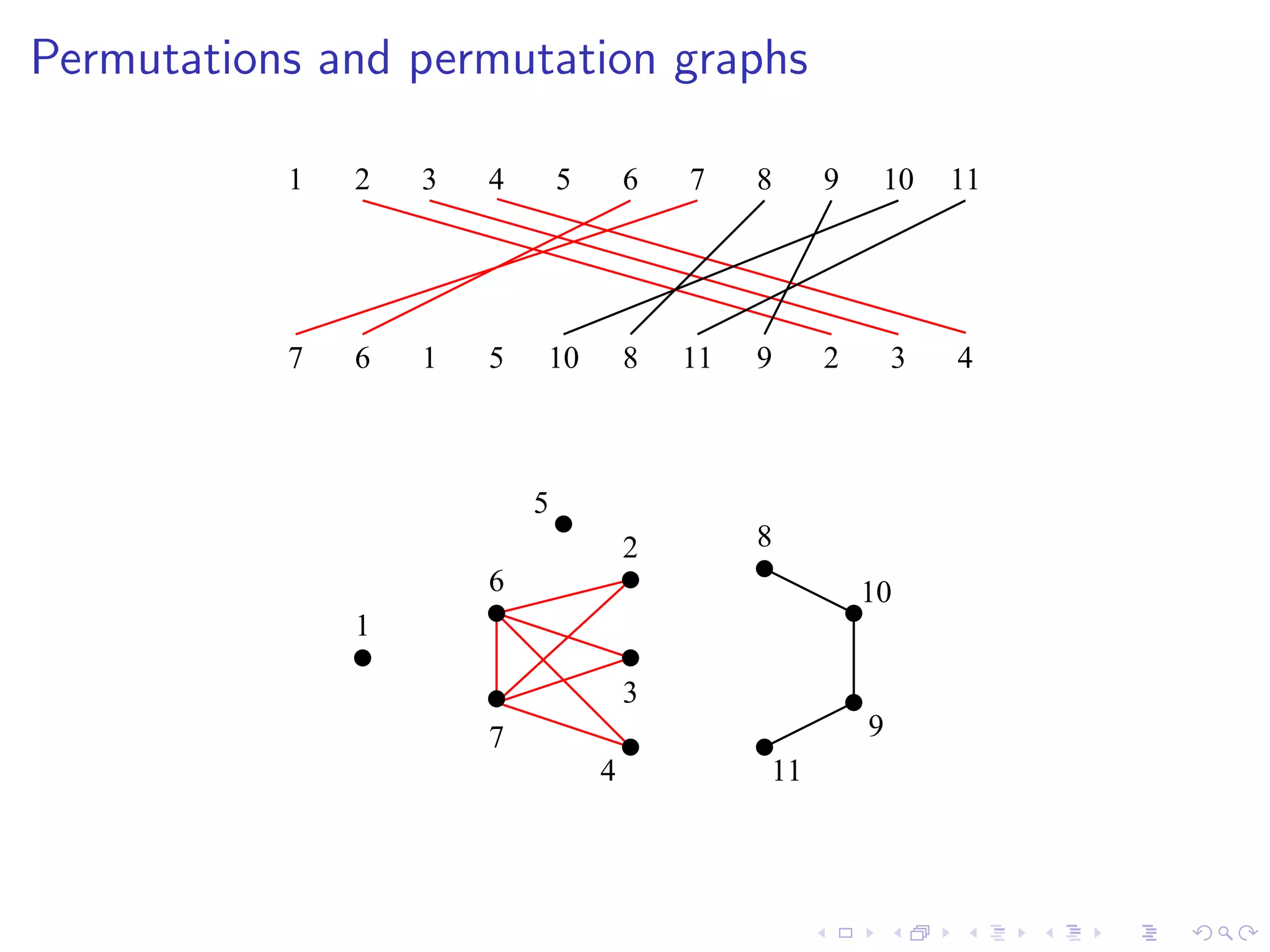
![Permutation graph recognition
Theorem [Gallai’67]
A permutation graph has a unique representation (up to reversal)
iff it is prime.
Recognition algorithm
Recursively solve the problem on modules
Solve the prime case (with linear time transitive orientation
algorithm)](https://image.slidesharecdn.com/04paul-120623180515-phpapp01/75/AlgoPerm2012-04-Christophe-Paul-12-2048.jpg)
![Permutation graph recognition
Theorem [Gallai’67]
A permutation graph has a unique representation (up to reversal)
iff it is prime.
Recognition algorithm
Recursively solve the problem on modules
Solve the prime case (with linear time transitive orientation
algorithm)
Theorem [McConnell and Spinrad’99]
The permutation graph recognition problem can be solved in
O(n + m) time
we need a linear time modular decomposition algorithm](https://image.slidesharecdn.com/04paul-120623180515-phpapp01/75/AlgoPerm2012-04-Christophe-Paul-13-2048.jpg)


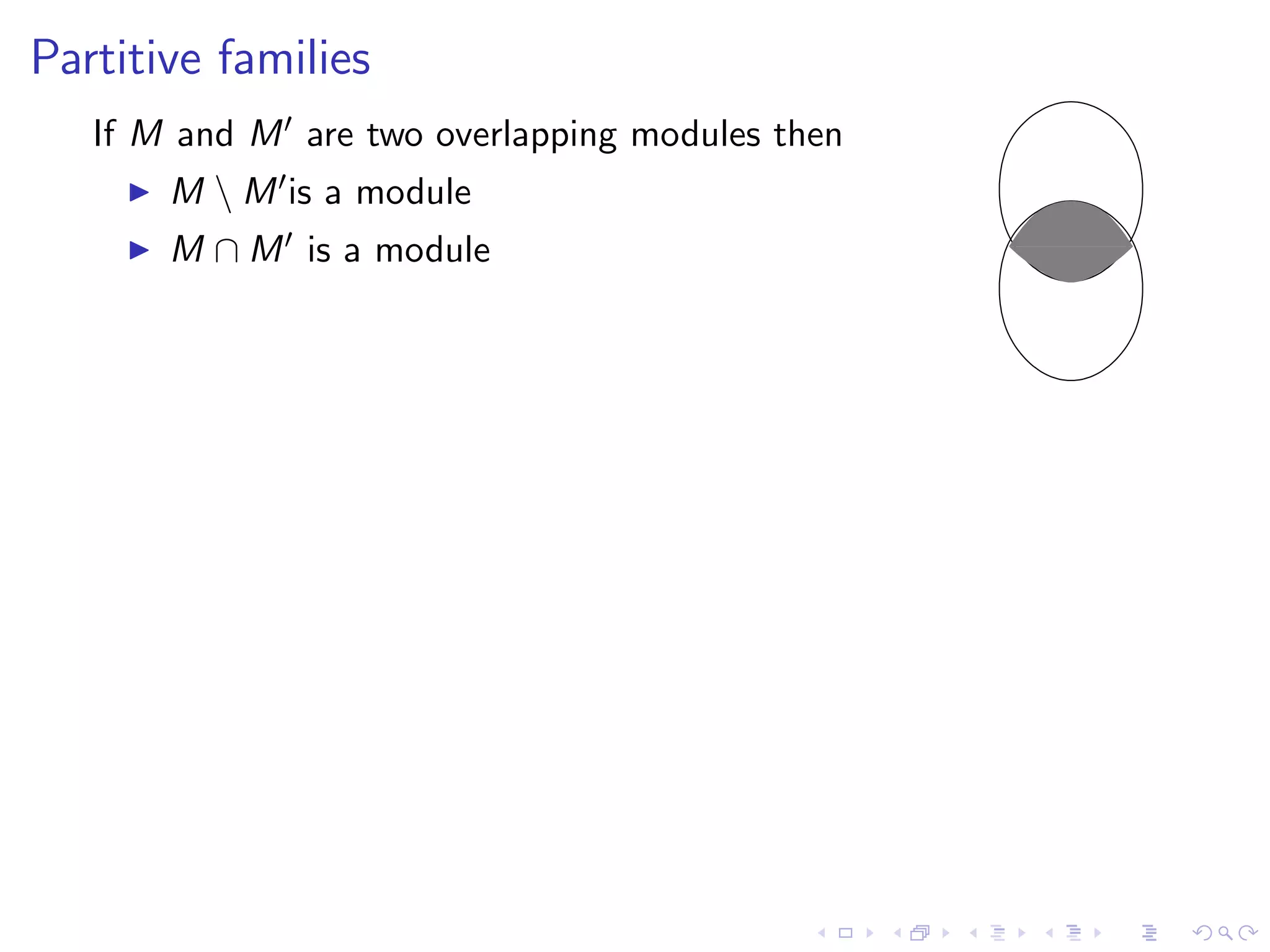

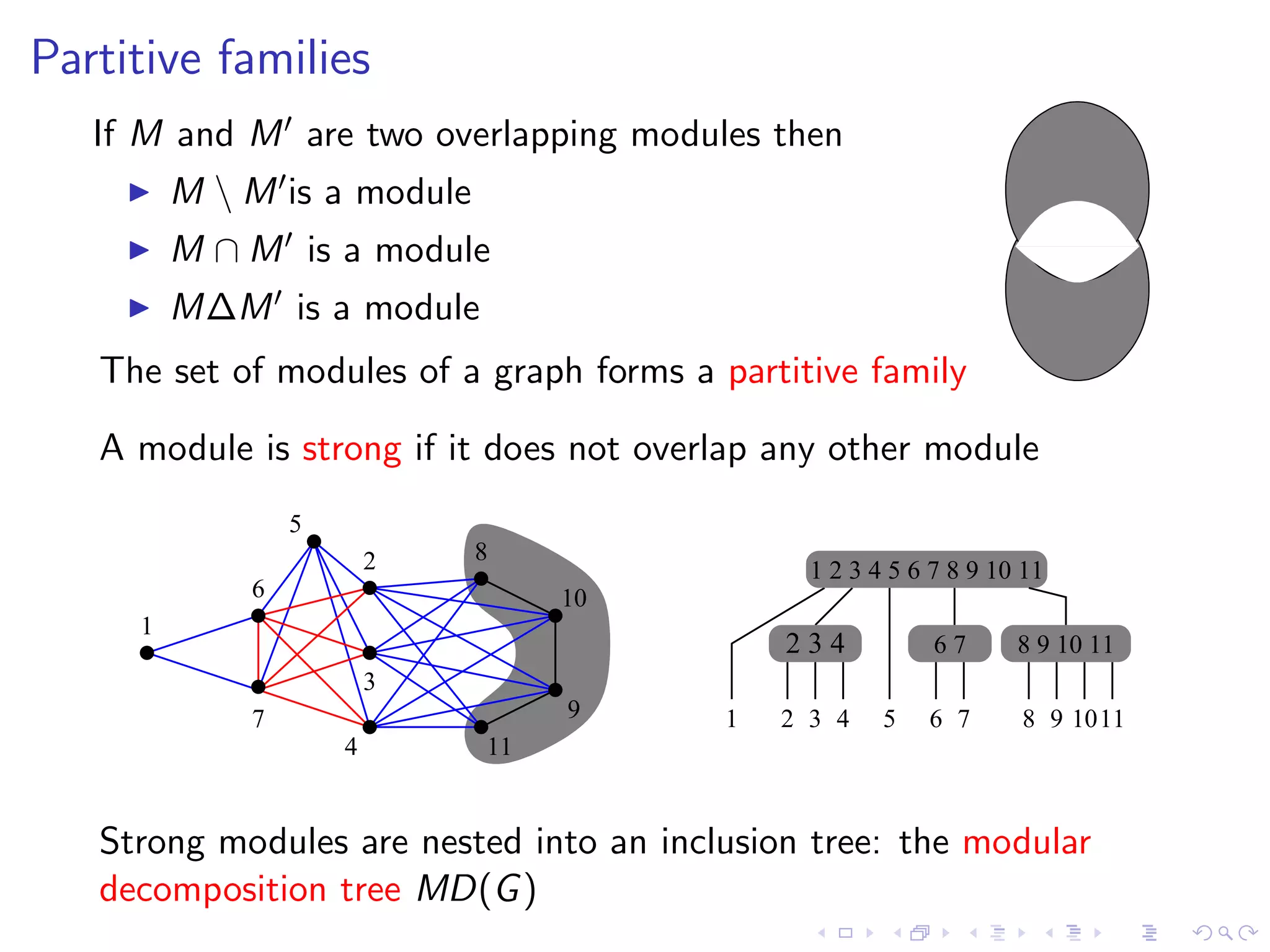
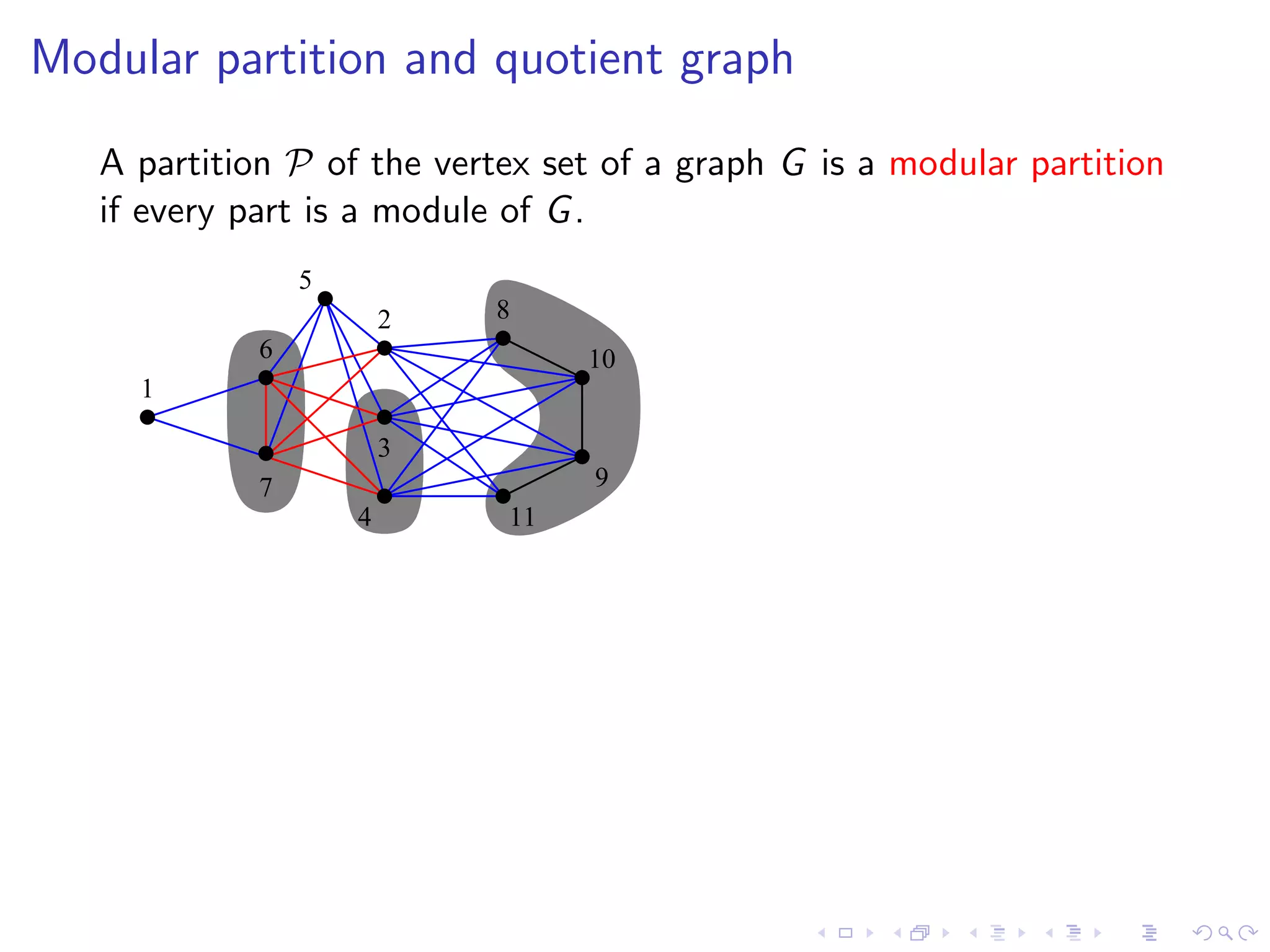
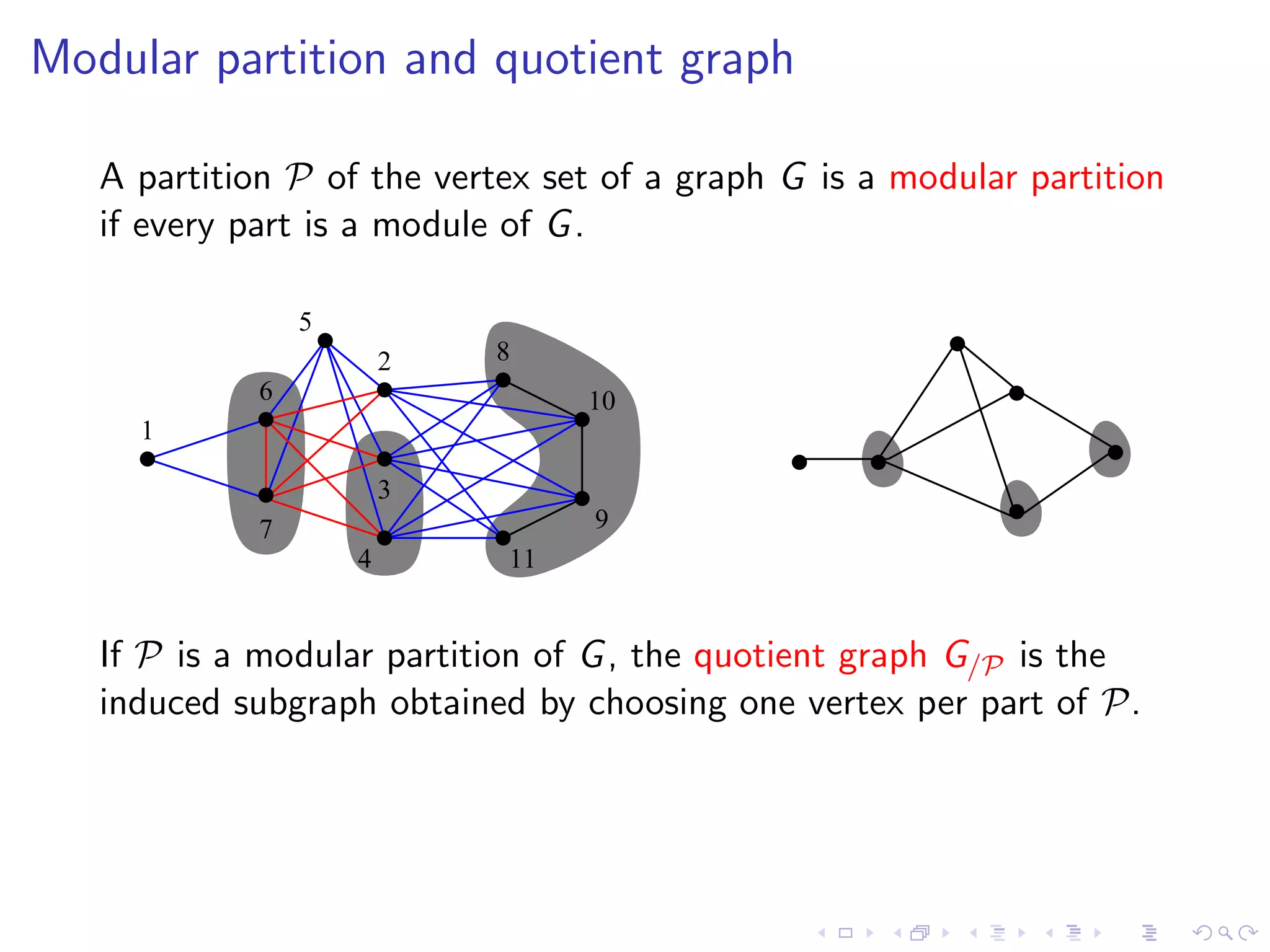
![Theorem [Gal’67,CHM81]
Let G = (V , E ) be a graph. Then either
1. (parallel) G is not connected, or
2. (series) G is not connected, or](https://image.slidesharecdn.com/04paul-120623180515-phpapp01/75/AlgoPerm2012-04-Christophe-Paul-21-2048.jpg)
![Theorem [Gal’67,CHM81]
Let G = (V , E ) be a graph. Then either
1. (parallel) G is not connected, or
2. (series) G is not connected, or
3. (prime) G/M(G ) is a prime graph, with M(G ) the modular
partition containing the maximal strong modules of G .
5 Prime
2 8 1 2 3 4 5 6 7 8 9 10 11
6 10
1
parallel series Prime
3 234 67 8 9 10 11
7 9
4 11 1 2 3 4 5 6 7 8 9 10 11](https://image.slidesharecdn.com/04paul-120623180515-phpapp01/75/AlgoPerm2012-04-Christophe-Paul-22-2048.jpg)
![Theorem [Gal’67,CHM81]
Let G = (V , E ) be a graph. Then either
1. (parallel) G is not connected, or
2. (series) G is not connected, or
3. (prime) G/M(G ) is a prime graph, with M(G ) the modular
partition containing the maximal strong modules of G .
5 Prime
2 8 1 2 3 4 5 6 7 8 9 10 11
6 10
1
parallel series Prime
3 234 67 8 9 10 11
7 9
4 11 1 2 3 4 5 6 7 8 9 10 11
Observation: If a P4 on {a, b, c, d} overlap a module M, then
|M ∩ {a, b, c, d}| = 1](https://image.slidesharecdn.com/04paul-120623180515-phpapp01/75/AlgoPerm2012-04-Christophe-Paul-23-2048.jpg)
![Modular decomposition algorithms
O(n4 ) [Cowan, James, Stanton’72]
O(n3 ) [Blass, 1978], [Habib, Maurer’79]
O(n2 ) [McConnell, Spinrad’89]](https://image.slidesharecdn.com/04paul-120623180515-phpapp01/75/AlgoPerm2012-04-Christophe-Paul-24-2048.jpg)
![Modular decomposition algorithms
O(n4 ) [Cowan, James, Stanton’72]
O(n3 ) [Blass, 1978], [Habib, Maurer’79]
O(n2 ) [McConnell, Spinrad’89]
O(n + mα(m, n)) [Spinrad’92], [Cournier, Habib’93]
O(n + m) [McConnell, Spinrad’94], [Cournier, Habib’94]](https://image.slidesharecdn.com/04paul-120623180515-phpapp01/75/AlgoPerm2012-04-Christophe-Paul-25-2048.jpg)
![Modular decomposition algorithms
O(n4 ) [Cowan, James, Stanton’72]
O(n3 ) [Blass, 1978], [Habib, Maurer’79]
O(n2 ) [McConnell, Spinrad’89]
O(n + mα(m, n)) [Spinrad’92], [Cournier, Habib’93]
O(n + m) [McConnell, Spinrad’94], [Cournier, Habib’94]
O(n + m log n) [Habib, Paul, Viennot’99] (factoring
permutation), [McConnell, Spinrad’00]](https://image.slidesharecdn.com/04paul-120623180515-phpapp01/75/AlgoPerm2012-04-Christophe-Paul-26-2048.jpg)
![Modular decomposition algorithms
O(n4 ) [Cowan, James, Stanton’72]
O(n3 ) [Blass, 1978], [Habib, Maurer’79]
O(n2 ) [McConnell, Spinrad’89]
O(n + mα(m, n)) [Spinrad’92], [Cournier, Habib’93]
O(n + m) [McConnell, Spinrad’94], [Cournier, Habib’94]
O(n + m log n) [Habib, Paul, Viennot’99] (factoring
permutation), [McConnell, Spinrad’00]
O(n + m) [Capelle, Habib’97] (factoring permutation)
[Dahlhaus, Gustedt, McConnell’97], [Tedder, Corneil, Habib,
Paul’08]
other many others for variants of modular decomposition](https://image.slidesharecdn.com/04paul-120623180515-phpapp01/75/AlgoPerm2012-04-Christophe-Paul-27-2048.jpg)
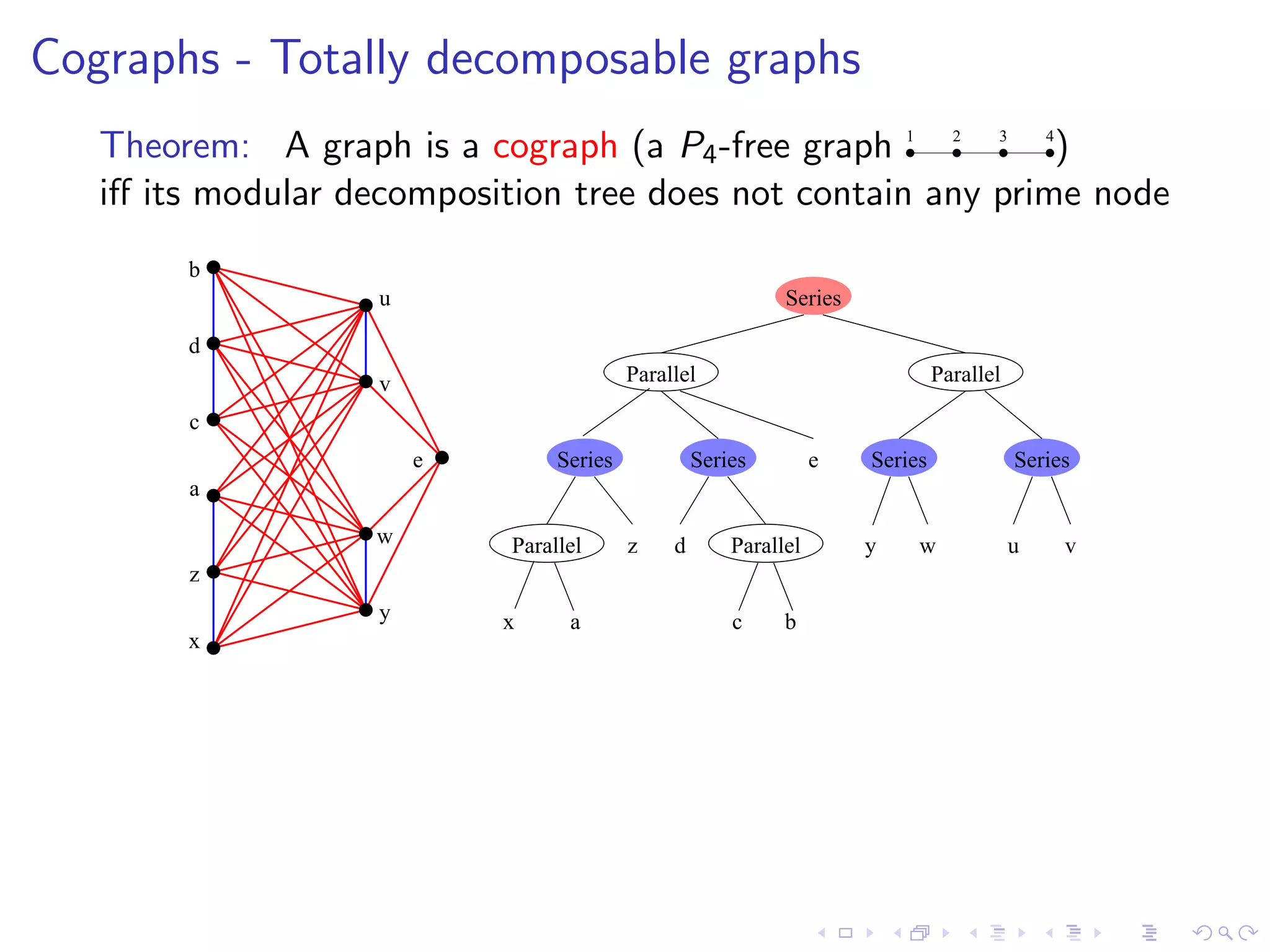
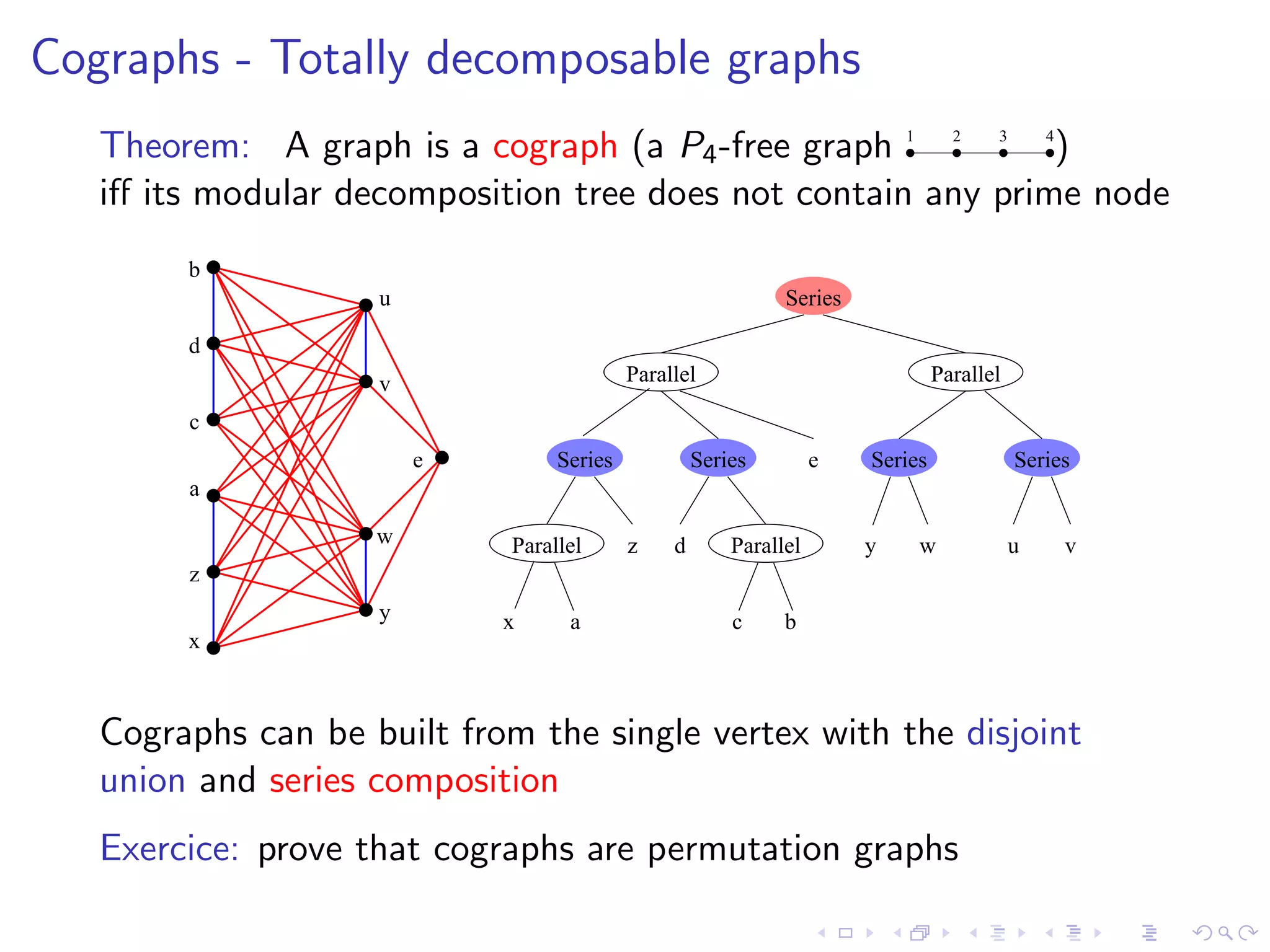
![Cographs - Totally decomposable graphs
Theorem: A graph is a cograph (a P4 -free graph 1 2 3 4)
iff its modular decomposition tree does not contain any prime node
b
u Series
d
v Parallel Parallel
c
e Series Series e Series Series
a
w Parallel z d Parallel y w u v
z
y x a c b
x
Linear time recognition algorithms
incremental [Corneil, Pearl, Stewart’85]
partition refinement [Habib, P.’05]
LexBFS [Bretscher, Corneil, Habib, P.’08]](https://image.slidesharecdn.com/04paul-120623180515-phpapp01/75/AlgoPerm2012-04-Christophe-Paul-30-2048.jpg)

![Ehrenfeucht et al’s modular decomposition algorithm
M(G , v ) is the modular partition composed by
{v } and the maximal modules of G not containing v .
series
prime parallel 8
9
8
9 A
@ A
@ C
B C
B
¡
¡
parallel series
series ! ! #
#
4
5
4
5 7
6 7
6
2
3
2
3
0
1
0
1
series ¢
£
¢
£
¨
©
¨
©
¦
§
¦
§
$
%
$
%
(
)
(
)
v ¤
¥
¤
¥
v
'
'
1. Compute M(G , v )
2. Compute MD(G/M(G ,v ) )
3. For each X ∈ M(G , v ) compute MD(G [X ])](https://image.slidesharecdn.com/04paul-120623180515-phpapp01/75/AlgoPerm2012-04-Christophe-Paul-32-2048.jpg)
![Computation of M(G , v ) (1)
Lemma [MR84] Let P be a modular partition of G = (V , E ).
X ⊆ P is a module of G/P iff ∪M∈X M is a module of G .
5
2 8
6 10
1
3
7 9
4 11](https://image.slidesharecdn.com/04paul-120623180515-phpapp01/75/AlgoPerm2012-04-Christophe-Paul-33-2048.jpg)
![Computation of M(G , v ) (1)
Lemma [MR84] Let P be a modular partition of G = (V , E ).
X ⊆ P is a module of G/P iff ∪M∈X M is a module of G .
A vertex x is a splitter for a set S of vertices if
∃y , z ∈ S with xy ∈ S and xz ∈ E /
We say that x separate y and z.
2
6
1 4
3
7](https://image.slidesharecdn.com/04paul-120623180515-phpapp01/75/AlgoPerm2012-04-Christophe-Paul-34-2048.jpg)
![Computation of M(G , v ) (1)
Lemma [MR84] Let P be a modular partition of G = (V , E ).
X ⊆ P is a module of G/P iff ∪M∈X M is a module of G .
A vertex x is a splitter for a set S of vertices if
∃y , z ∈ S with xy ∈ S and xz ∈ E /
We say that x separate y and z.
2
6 Lemma If x is a splitter for the set
1 4 S, then any module M containing S
must also contain x.
3
7](https://image.slidesharecdn.com/04paul-120623180515-phpapp01/75/AlgoPerm2012-04-Christophe-Paul-35-2048.jpg)






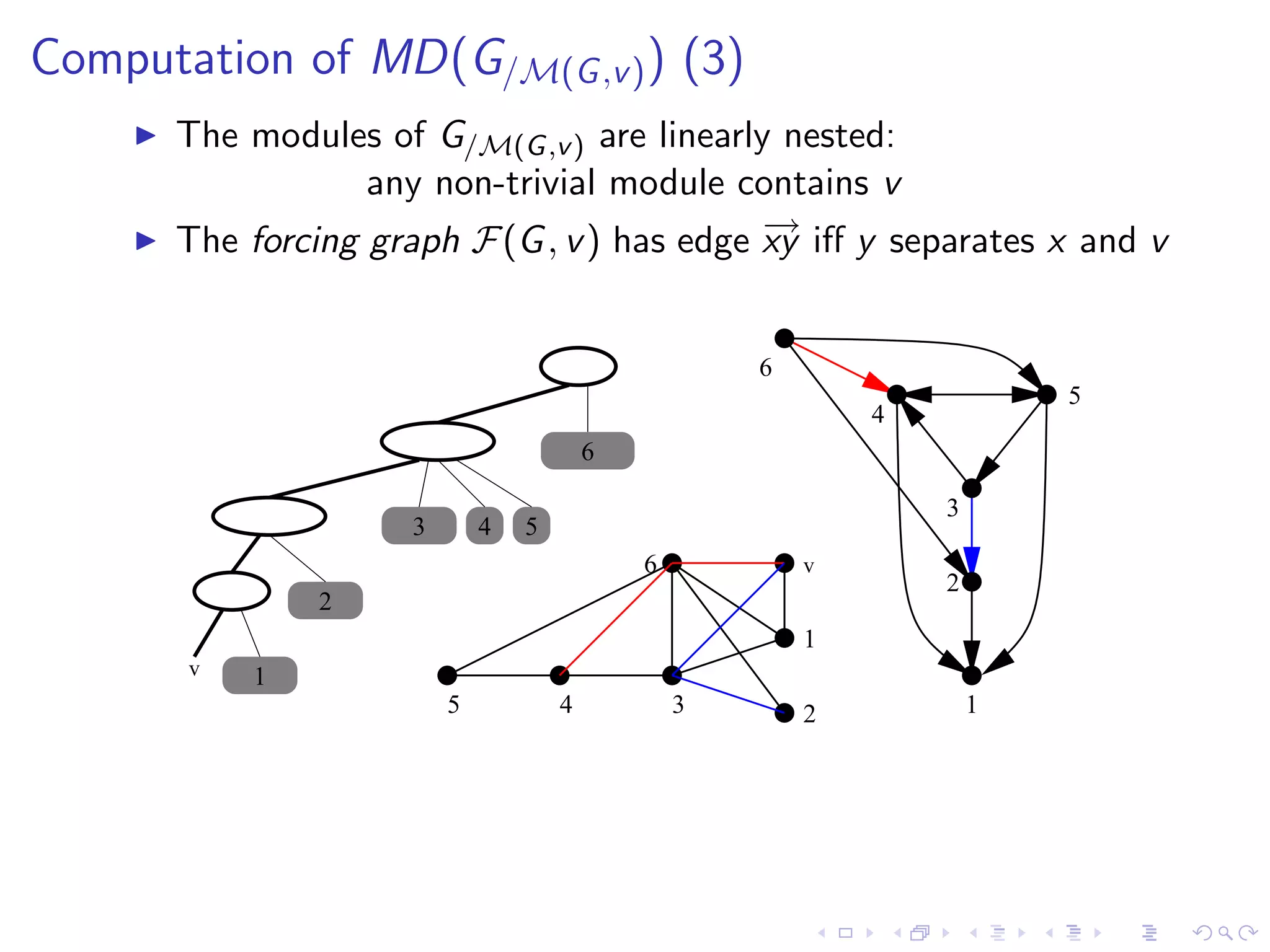
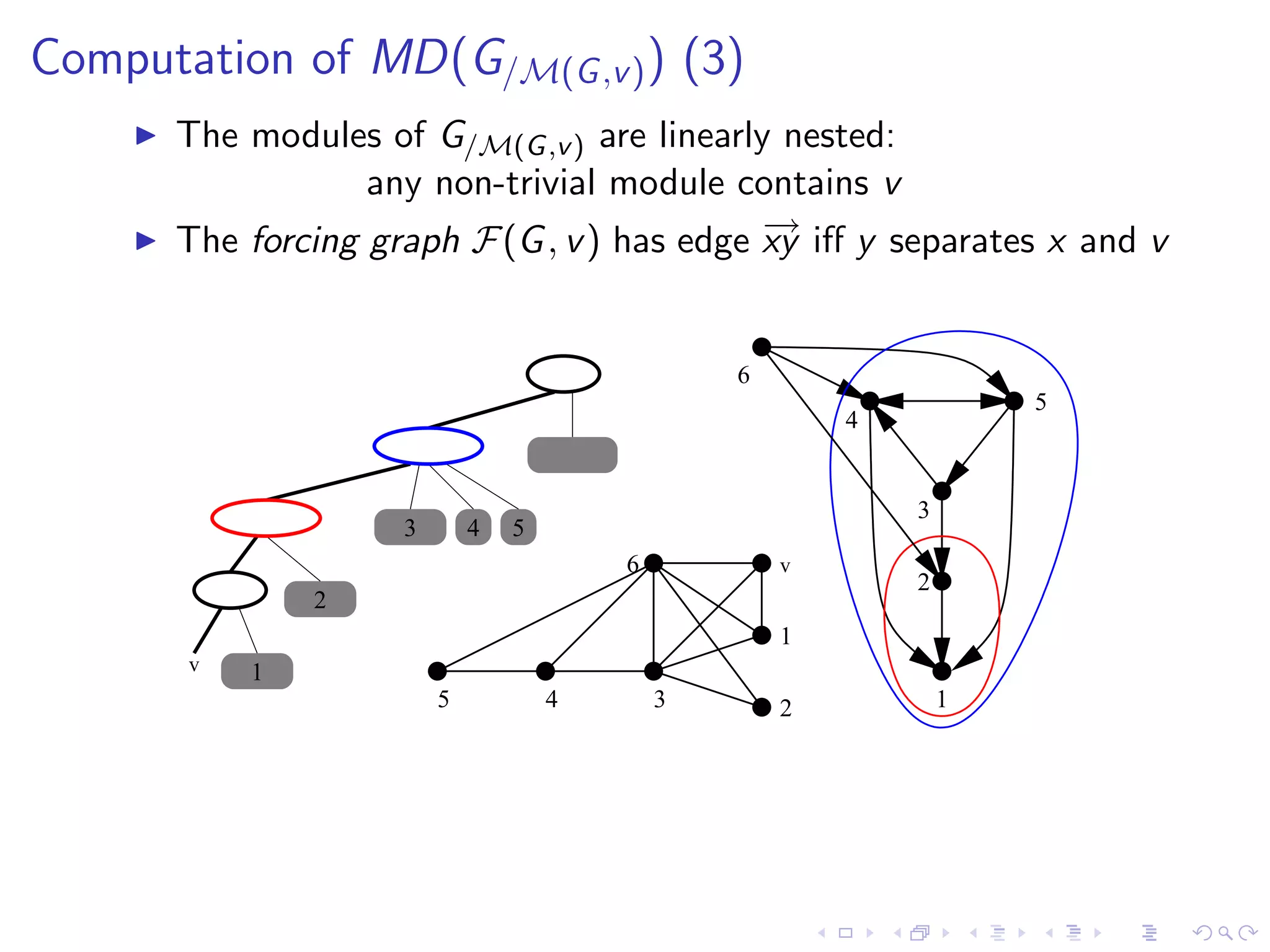
![Computation of MD(G/M(G ,v ) ) (4)
Complexity
[Ehrenfeucht et al.’94] gives a O(n2 ) complexity.
[MS00]: simple O(n + m log n) vertex partitioning algorithm
[DGM’01]: O(n + m.α(n, m)) and a more complicated
O(n + m) implementation.
Other algorithms
[CH94] and [MS94]: the first linear algorithms.
[MS99]: O(n + m) algorithm which extends to transitive
orientation.](https://image.slidesharecdn.com/04paul-120623180515-phpapp01/75/AlgoPerm2012-04-Christophe-Paul-44-2048.jpg)
![Computation of MD(G/M(G ,v ) ) (4)
Complexity
[Ehrenfeucht et al.’94] gives a O(n2 ) complexity.
[MS00]: simple O(n + m log n) vertex partitioning algorithm
[DGM’01]: O(n + m.α(n, m)) and a more complicated
O(n + m) implementation.
Other algorithms
[CH94] and [MS94]: the first linear algorithms.
[MS99]: O(n + m) algorithm which extends to transitive
orientation.
[Spinrad’03] The new [linear time] algorithm [MS99] is currently
too complex to describe easily [...] I hope and believe that in a
number of years the linear algorithm can be simplified as well.
[Tedder, Corneil, Habib, P.’08] simple linear time algorithm](https://image.slidesharecdn.com/04paul-120623180515-phpapp01/75/AlgoPerm2012-04-Christophe-Paul-45-2048.jpg)

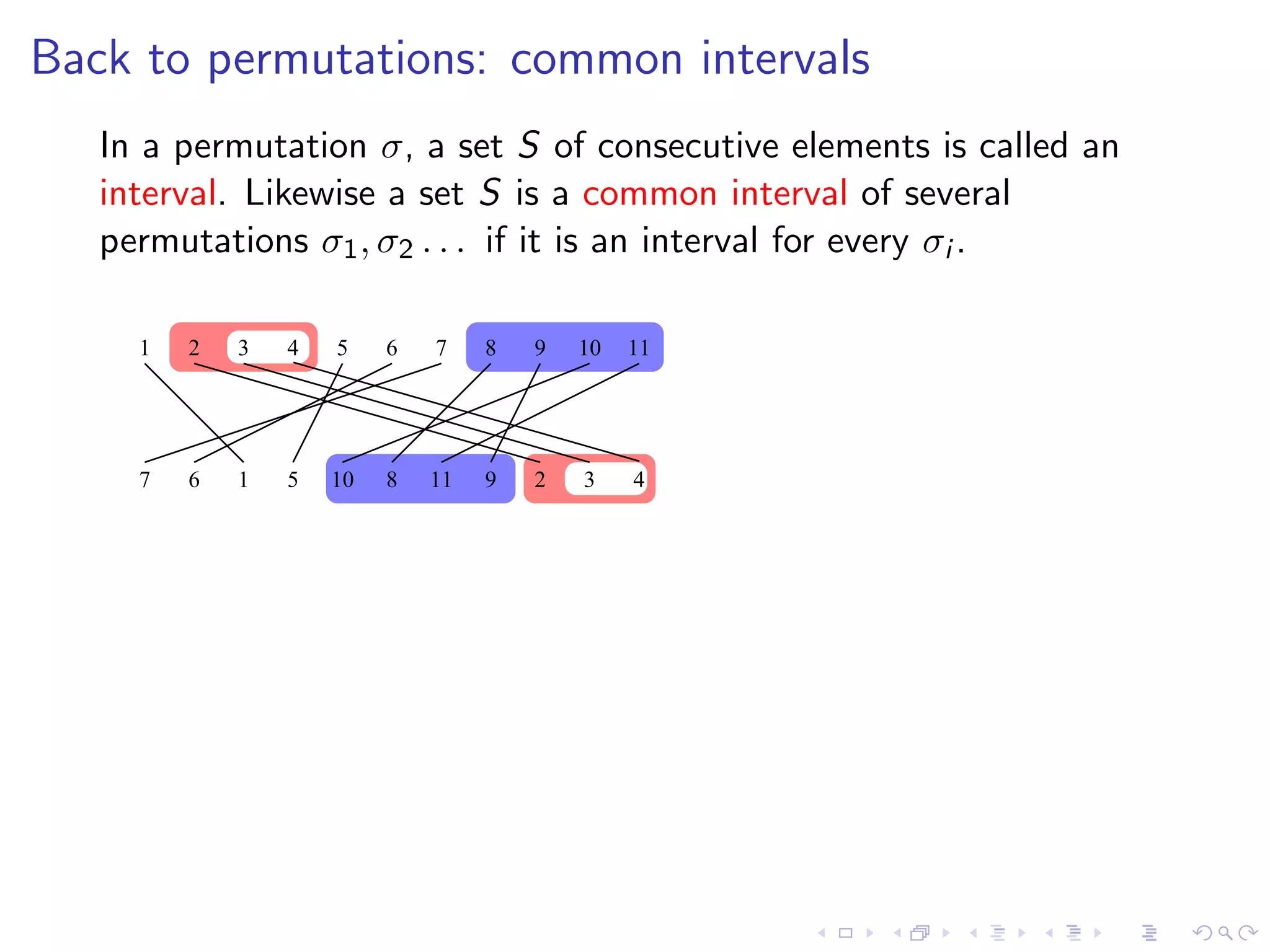
![Back to permutations: common intervals
In a permutation σ, a set S of consecutive elements is called an
interval. Likewise a set S is a common interval of several
permutations σ1 , σ2 . . . if it is an interval for every σi .
5
2 8
1 2 3 4 5 6 7 8 9 10 11
6 10
1
3
7 6 1 5 10 8 11 9 2 3 4 7 9
4 11
Obs.: common intervals of σ1 , σ2 are not modules of G (σ1 , σ2 )
Computation of all common intervals in linear time - O(n2 ) -
[Uno, Yagura’00]](https://image.slidesharecdn.com/04paul-120623180515-phpapp01/75/AlgoPerm2012-04-Christophe-Paul-49-2048.jpg)
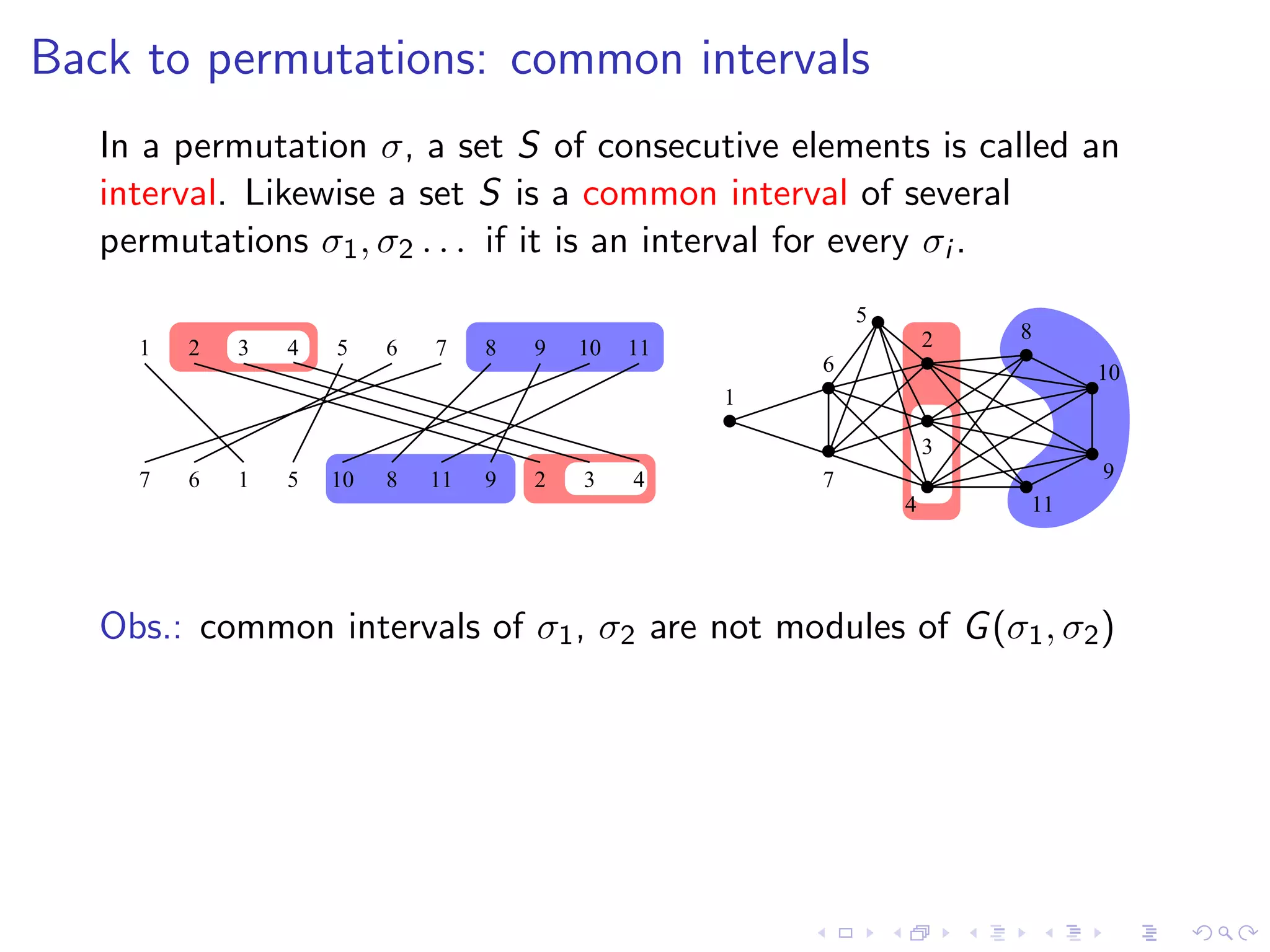
![Back to permutations: common intervals
In a permutation σ, a set S of consecutive elements is called an
interval. Likewise a set S is a common interval of several
permutations σ1 , σ2 . . . if it is an interval for every σi .
5
2 8
1 2 3 4 5 6 7 8 9 10 11
6 10
1
3
7 6 1 5 10 8 11 9 2 3 4 7 9
4 11
Obs.: common intervals of σ1 , σ2 are not modules of G (σ1 , σ2 )
Strong (common) interval doesn’t overlap other common intervals
Lemma [de Montgolfier] A set S is a strong interval of σ1 and σ2
iff it is a strong module of the permutation graph G (σ1 , σ2 )](https://image.slidesharecdn.com/04paul-120623180515-phpapp01/75/AlgoPerm2012-04-Christophe-Paul-50-2048.jpg)

![Common intervals (2)
The family of common intervals is weakly partitive:
7 1 6 5 4 3 2 9 8 11 10
7 1 5 3 8
if I1 and I2 are two common intervals then
I1 ∪ I2 is a common interval
I1 ∩ I2 is a common interval
I1 I2 and I2 I1 are common intervals
Let I be a partition of [1 . . . n] into common intervals of the
permutation σ, then we denote by σ/I the quotient permutation
defined on [1 . . . |I|]](https://image.slidesharecdn.com/04paul-120623180515-phpapp01/75/AlgoPerm2012-04-Christophe-Paul-52-2048.jpg)
![Common intervals (2)
The family of common intervals is weakly partitive:
7 1 6 5 4 3 2 9 8 11 10
4 1 3 2 5
if I1 and I2 are two common intervals then
I1 ∪ I2 is a common interval
I1 ∩ I2 is a common interval
I1 I2 and I2 I1 are common intervals
Let I be a partition of [1 . . . n] into common intervals of the
permutation σ, then we denote by σ/I the quotient permutation
defined on [1 . . . |I|]](https://image.slidesharecdn.com/04paul-120623180515-phpapp01/75/AlgoPerm2012-04-Christophe-Paul-53-2048.jpg)
![Common intervals (3)
Theorem Let σ be a permutation on [1, . . . n] and I be the
partition into maximal common intervals of σ, then either
1. σ/I = 1|I| - the identity on [1 . . . |I|]
2. σ/I = 1|I| - the reverse identity on [1 . . . |I|]
3. σ/I is prime - or simple (does not have non-trivial common
interval)](https://image.slidesharecdn.com/04paul-120623180515-phpapp01/75/AlgoPerm2012-04-Christophe-Paul-54-2048.jpg)
![Common intervals (3)
Theorem Let σ be a permutation on [1, . . . n] and I be the
partition into maximal common intervals of σ, then either
1. σ/I = 1|I| - the identity on [1 . . . |I|]
2. σ/I = 1|I| - the reverse identity on [1 . . . |I|]
3. σ/I is prime - or simple (does not have non-trivial common
interval)
7 1 6 5 4 3 2 9 8 11 10
Theorem (see e.g. [Bergeron et al.’08])
The common interval tree can be computed in O(n) time.](https://image.slidesharecdn.com/04paul-120623180515-phpapp01/75/AlgoPerm2012-04-Christophe-Paul-55-2048.jpg)




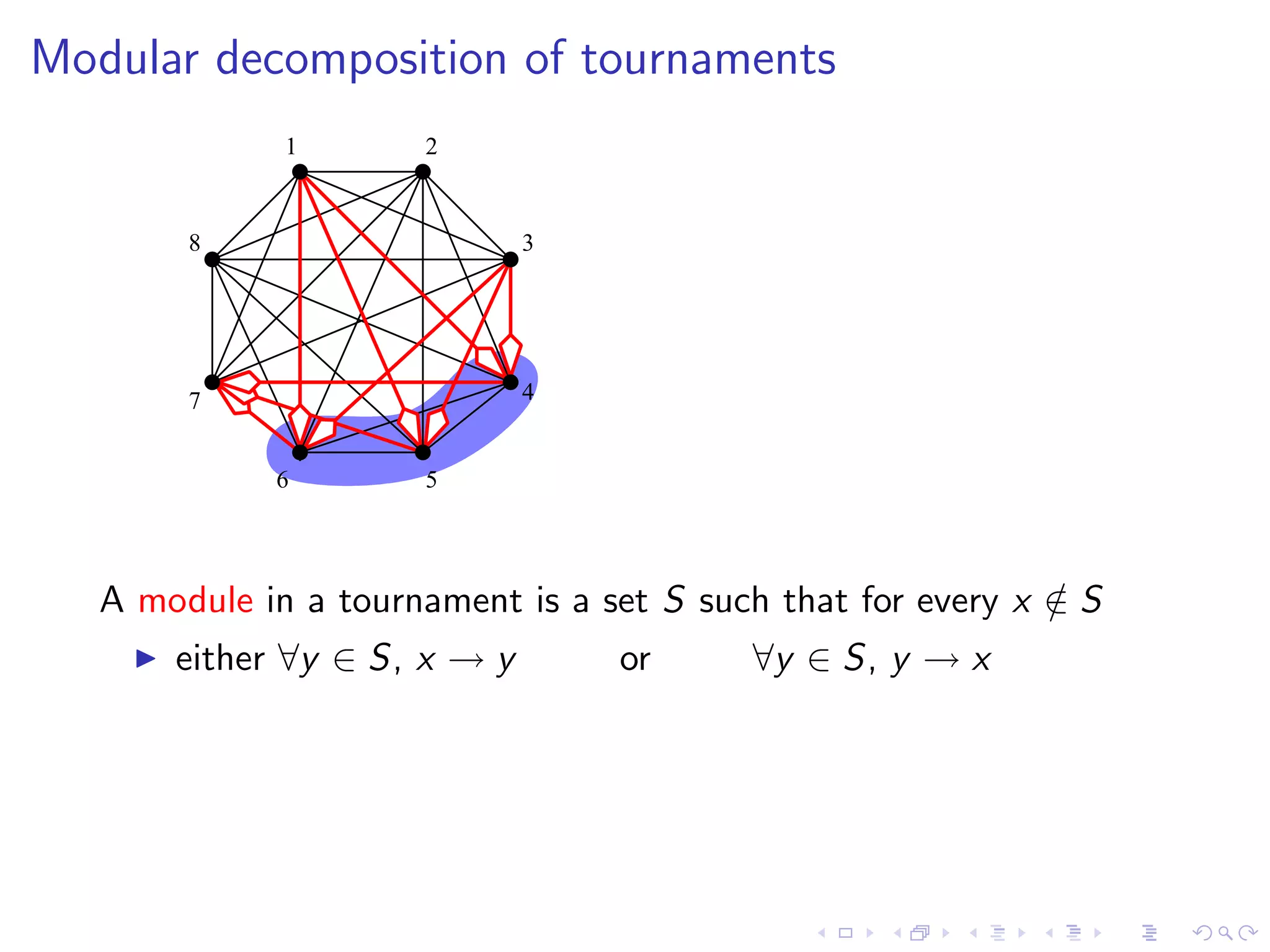
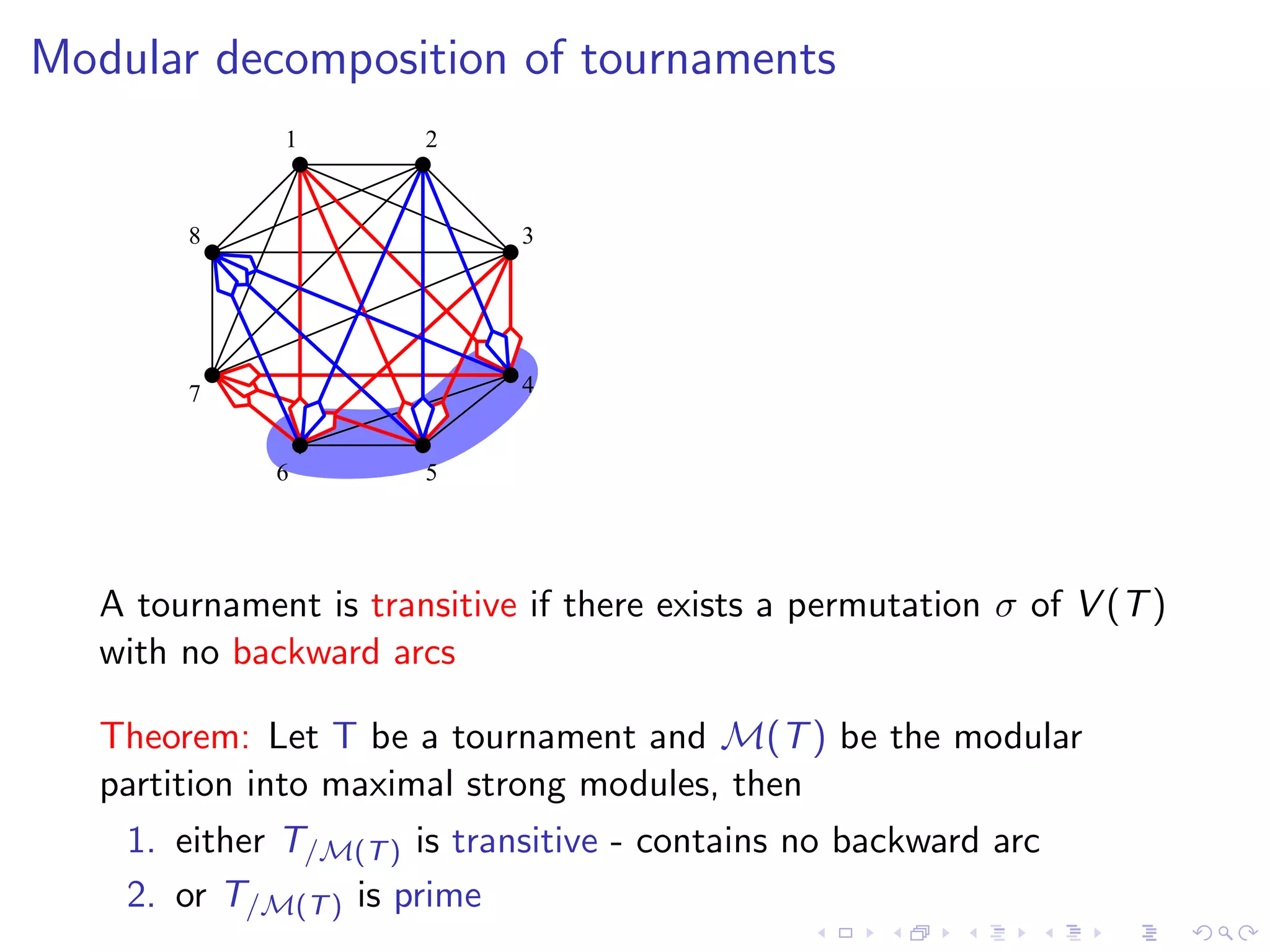
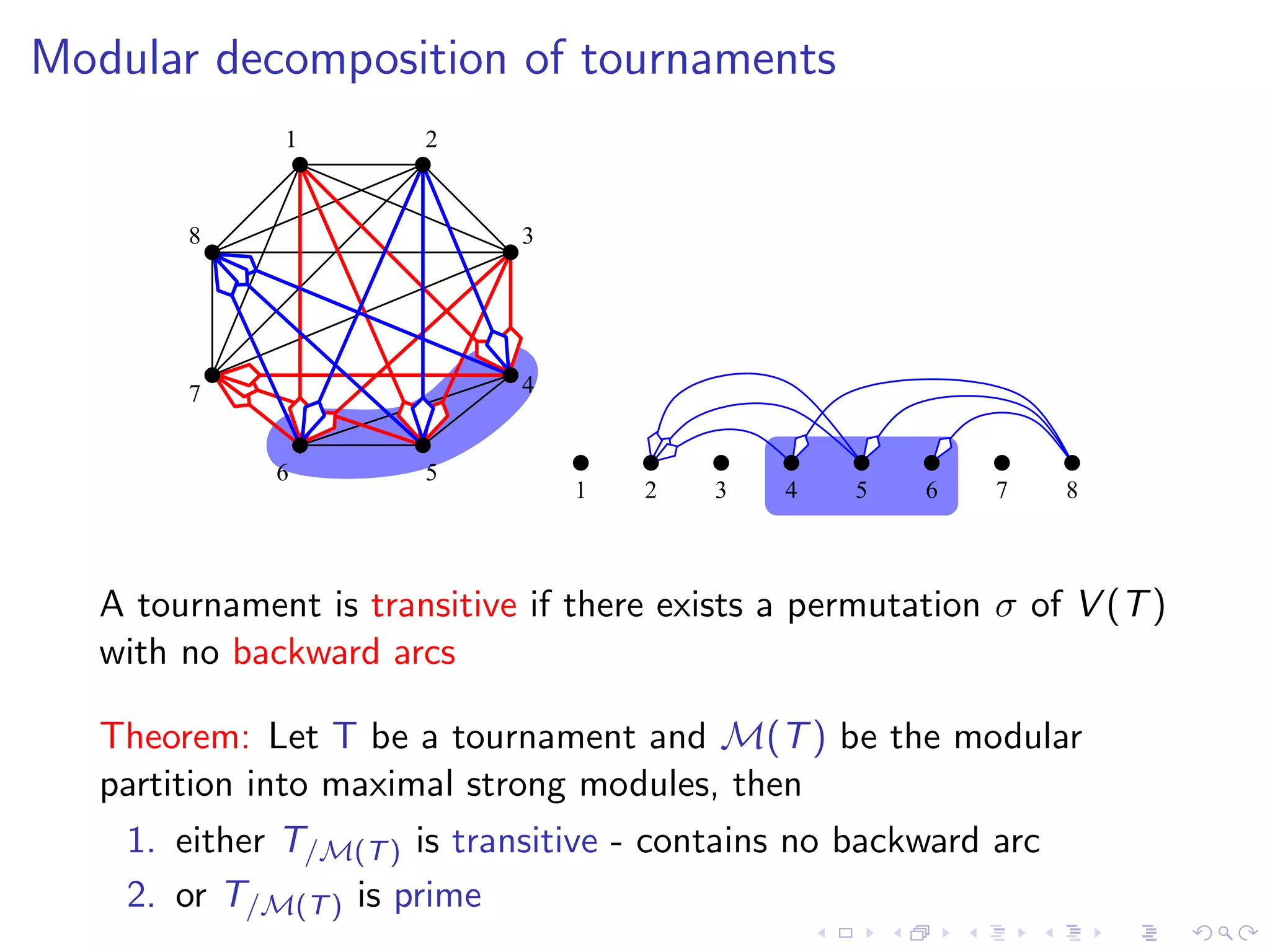

![Modular decomposition algorithm for tournaments
A factoring permutation of a tournament T (or a graph) is a
permutation σ of its vertices such that
every (strong) module of T is an interval of σ
Factoring permutation via a partition refinement algorithm in
linear time [de Mongolfier’03]
1 2 3 4 5 6 7 8](https://image.slidesharecdn.com/04paul-120623180515-phpapp01/75/AlgoPerm2012-04-Christophe-Paul-65-2048.jpg)
![Modular decomposition algorithm for tournaments
A factoring permutation of a tournament T (or a graph) is a
permutation σ of its vertices such that
every (strong) module of T is an interval of σ
Factoring permutation via a partition refinement algorithm in
linear time [de Mongolfier’03]
3 4 5 6 1 2 7 8](https://image.slidesharecdn.com/04paul-120623180515-phpapp01/75/AlgoPerm2012-04-Christophe-Paul-66-2048.jpg)
![Modular decomposition algorithm for tournaments
A factoring permutation of a tournament T (or a graph) is a
permutation σ of its vertices such that
every (strong) module of T is an interval of σ
Factoring permutation via a partition refinement algorithm in
linear time [de Mongolfier’03]
4 3 5 6 1 2 8 7](https://image.slidesharecdn.com/04paul-120623180515-phpapp01/75/AlgoPerm2012-04-Christophe-Paul-67-2048.jpg)
![Modular decomposition algorithm for tournaments
A factoring permutation of a tournament T (or a graph) is a
permutation σ of its vertices such that
every (strong) module of T is an interval of σ
Factoring permutation via a partition refinement algorithm in
linear time [de Mongolfier’03]
4 3 5 6 1 2 8 7](https://image.slidesharecdn.com/04paul-120623180515-phpapp01/75/AlgoPerm2012-04-Christophe-Paul-68-2048.jpg)
![Modular decomposition algorithm for tournaments
A factoring permutation of a tournament T (or a graph) is a
permutation σ of its vertices such that
every (strong) module of T is an interval of σ
Factoring permutation via a partition refinement algorithm in
linear time [de Mongolfier’03]
4 3 5 6 1 2 8 7
Modular decomposition tree from a factoring permutation in
linear time [Capelle’97]](https://image.slidesharecdn.com/04paul-120623180515-phpapp01/75/AlgoPerm2012-04-Christophe-Paul-69-2048.jpg)



![FAST: Feedback Arc Set in Tournament
A tournament T and an integer k
Find a permutation σ of the vertices with at most k backward
edges
1 2 3 4 5 6 7 8
NP-Complete [Alon’06] [Charbit et al.’07]
FTP [Raman, Saurabh’06] [Alon et al.’09]
(1 + )-approximation scheme [Kenyon-Mathieu, Schudy’07]](https://image.slidesharecdn.com/04paul-120623180515-phpapp01/75/AlgoPerm2012-04-Christophe-Paul-73-2048.jpg)
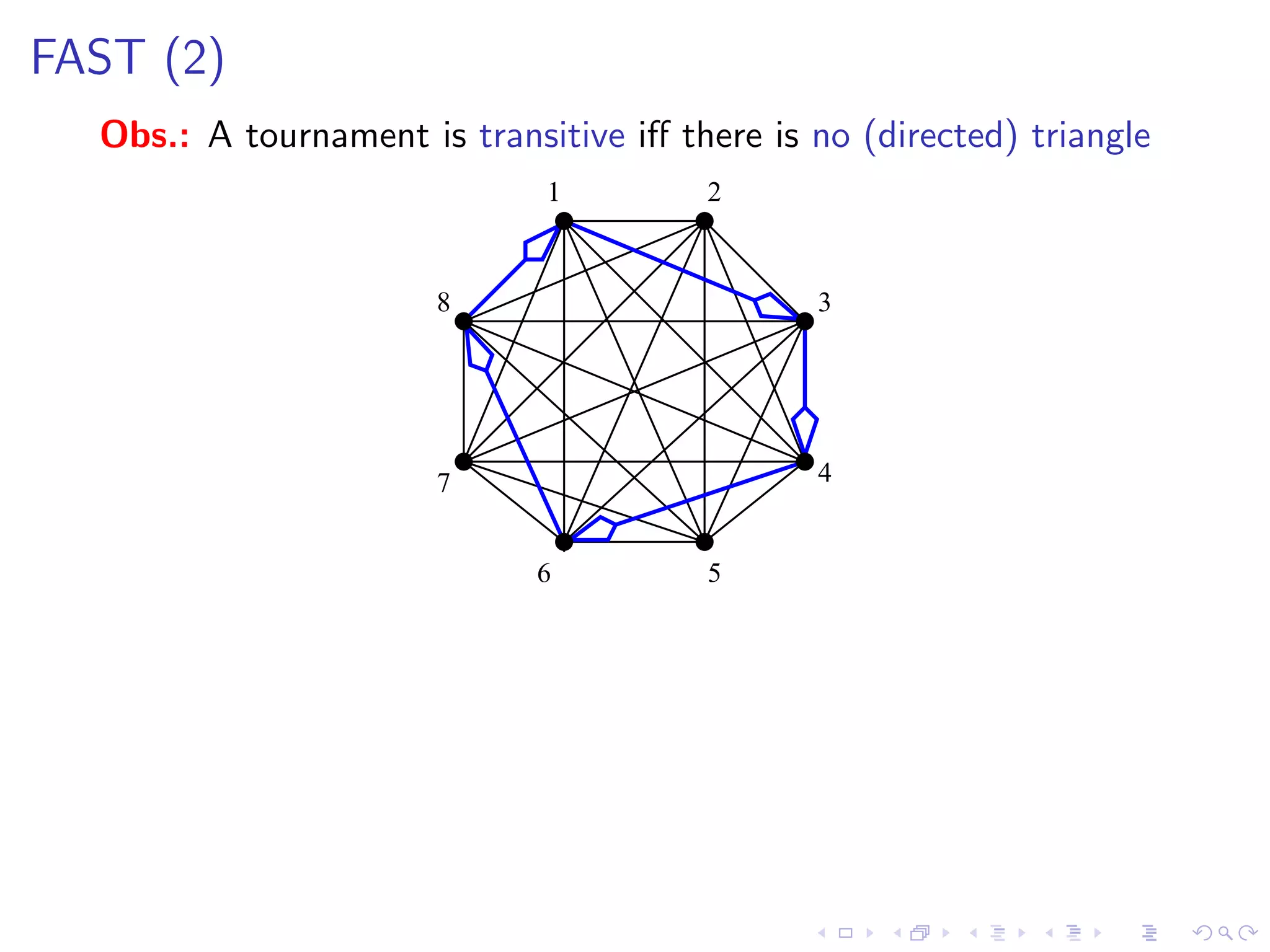
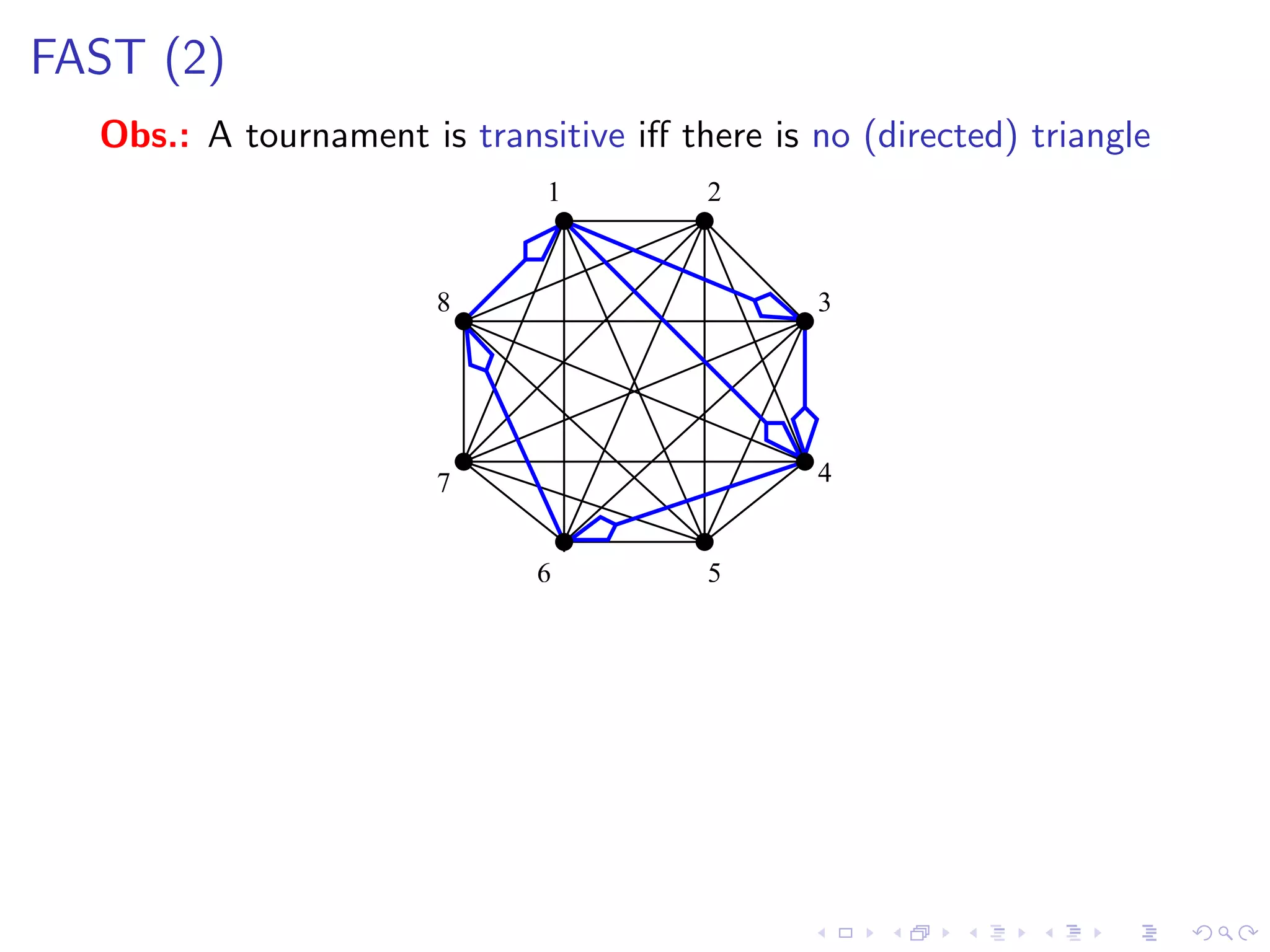
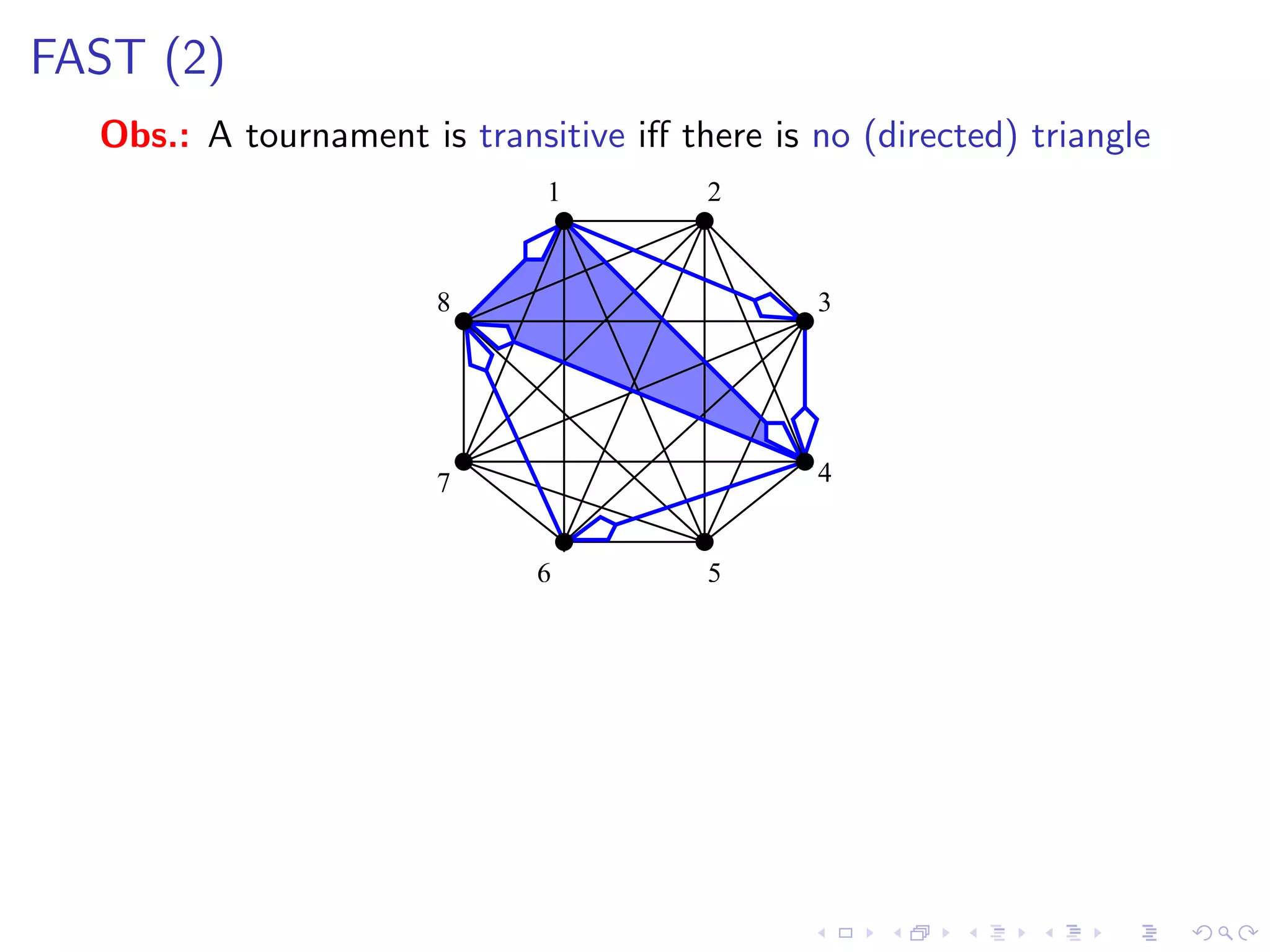
![FAST (2)
Obs.: A tournament is transitive iff there is no (directed) triangle
Rule 1 [irrelevant vertex] If a vertex v is not contained in any
triangle, then delete v
Rule 2 [sunflower] If there is an arc
belonging to more that k distinct triangles,
then reverse it and decrease k by 1](https://image.slidesharecdn.com/04paul-120623180515-phpapp01/75/AlgoPerm2012-04-Christophe-Paul-77-2048.jpg)
![FAST (2)
Obs.: A tournament is transitive iff there is no (directed) triangle
Rule 1 [irrelevant vertex] If a vertex v is not contained in any
triangle, then delete v
A reduced tournament contains no source nor sink
Rule 2 [sunflower] If there is an arc
belonging to more that k distinct triangles,
then reverse it and decrease k by 1
The span s(− ) of a backward arc of a reduced tournament is
→
uv 2k + 2](https://image.slidesharecdn.com/04paul-120623180515-phpapp01/75/AlgoPerm2012-04-Christophe-Paul-78-2048.jpg)
![FAST (3)
Rule 3 [acyclic module] Let M be a maximal acyclic module.
If there are at most p = |M| arcs from N + (M) to N − (M),
then reverse all these arcs and decrease k by p.](https://image.slidesharecdn.com/04paul-120623180515-phpapp01/75/AlgoPerm2012-04-Christophe-Paul-79-2048.jpg)
![FAST (3)
Rule 3 [acyclic module] Let M be a maximal acyclic module.
If there are at most p = |M| arcs from N + (M) to N − (M),
then reverse all these arcs and decrease k by p.](https://image.slidesharecdn.com/04paul-120623180515-phpapp01/75/AlgoPerm2012-04-Christophe-Paul-80-2048.jpg)
![FAST (3)
Rule 3 [acyclic module] Let M be a maximal acyclic module.
If there are at most p = |M| arcs from N + (M) to N − (M),
then reverse all these arcs and decrease k by p.
acyclic module Rule ⇒
ti2 s(− )
→
uv
ti](https://image.slidesharecdn.com/04paul-120623180515-phpapp01/75/AlgoPerm2012-04-Christophe-Paul-81-2048.jpg)
![FAST (3)
Rule 3 [acyclic module] Let M be a maximal acyclic module.
If there are at most p = |M| arcs from N + (M) to N − (M),
then reverse all these arcs and decrease k by p.
sunflower Rule ⇒
ti2 s(− )
→
uv k(2k + 2)](https://image.slidesharecdn.com/04paul-120623180515-phpapp01/75/AlgoPerm2012-04-Christophe-Paul-82-2048.jpg)
![FAST (3)
Rule 3 [acyclic module] Let M be a maximal acyclic module.
If there are at most p = |M| arcs from N + (M) to N − (M),
then reverse all these arcs and decrease k by p.
sunflower Rule ⇒
ti2 s(− )
→
uv k(2k + 2)
Theorem [Bessy et al.’09]: Every instance (T , k) of k-FAST can
be reduced in polynomial time to an equivalent instance (T , k )
such that √
|T | 2k + ti = O(k k) and k k](https://image.slidesharecdn.com/04paul-120623180515-phpapp01/75/AlgoPerm2012-04-Christophe-Paul-83-2048.jpg)

![Kernelization algorithm
poly time
(G,k) (G’,k’)
|G’¦=f(k)
Given a parameterized instance (I, k) of a problem, a kernelization
algorithm computes in polytime an equivalent instance (I , k ) st.
k = f (k) and |I | g (k)
√
we described a O(k k)-vertex kernel for FAST based on
modular decomposition
best known result: O(k)-vertex kernel ([Bessy et al.’09], [P.,
Perez, Thomass´’11])
e](https://image.slidesharecdn.com/04paul-120623180515-phpapp01/75/AlgoPerm2012-04-Christophe-Paul-85-2048.jpg)







