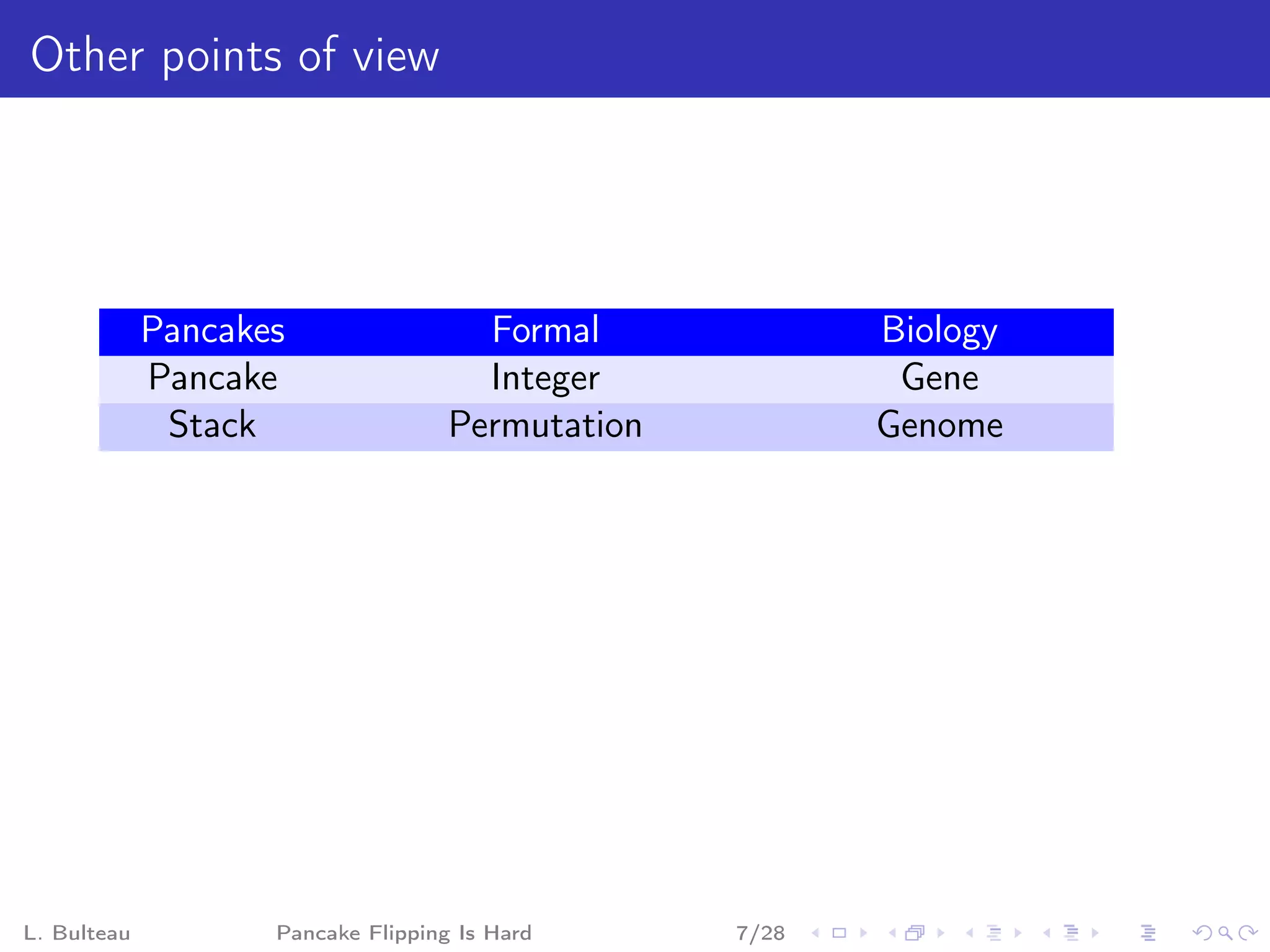
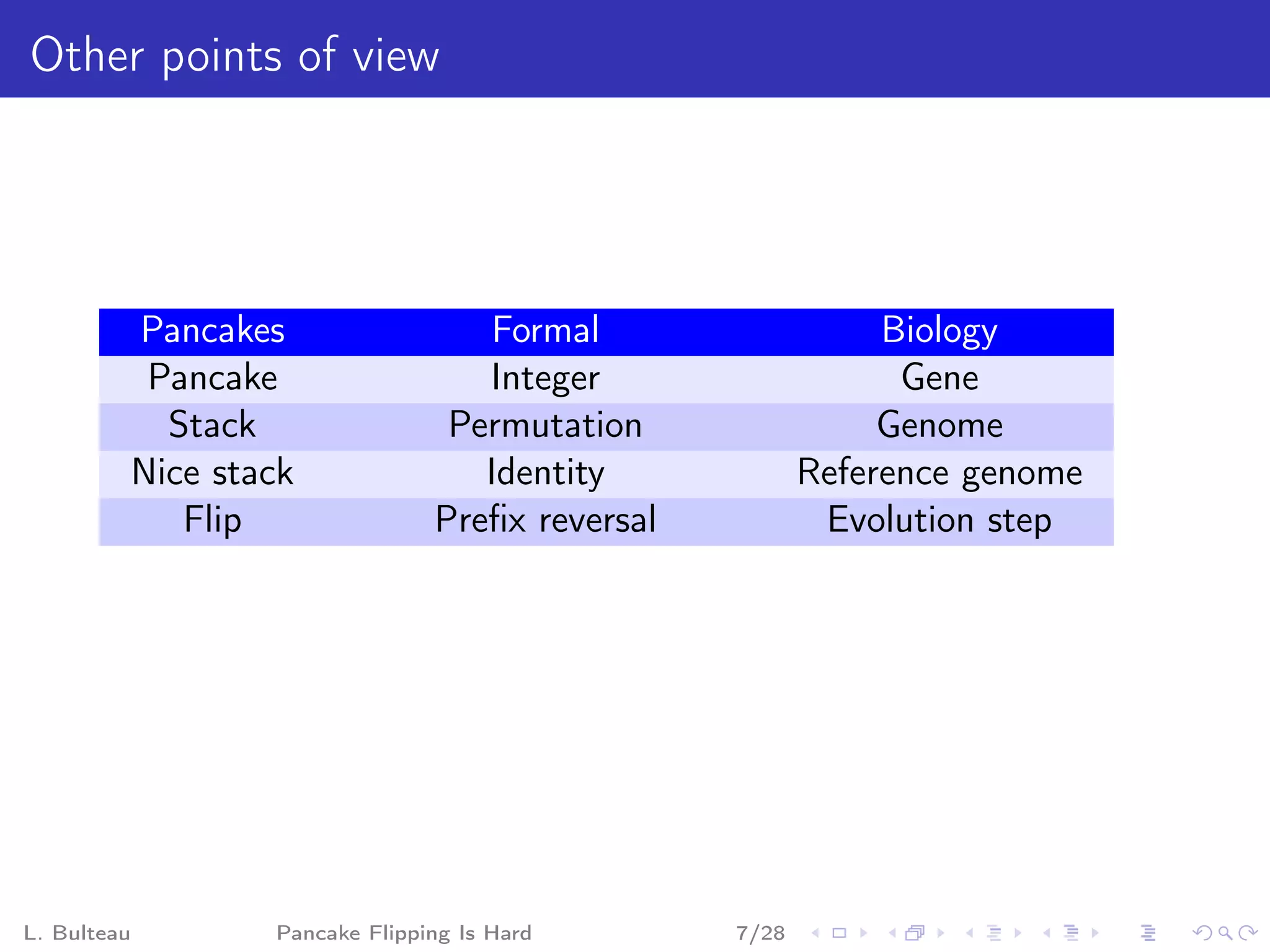
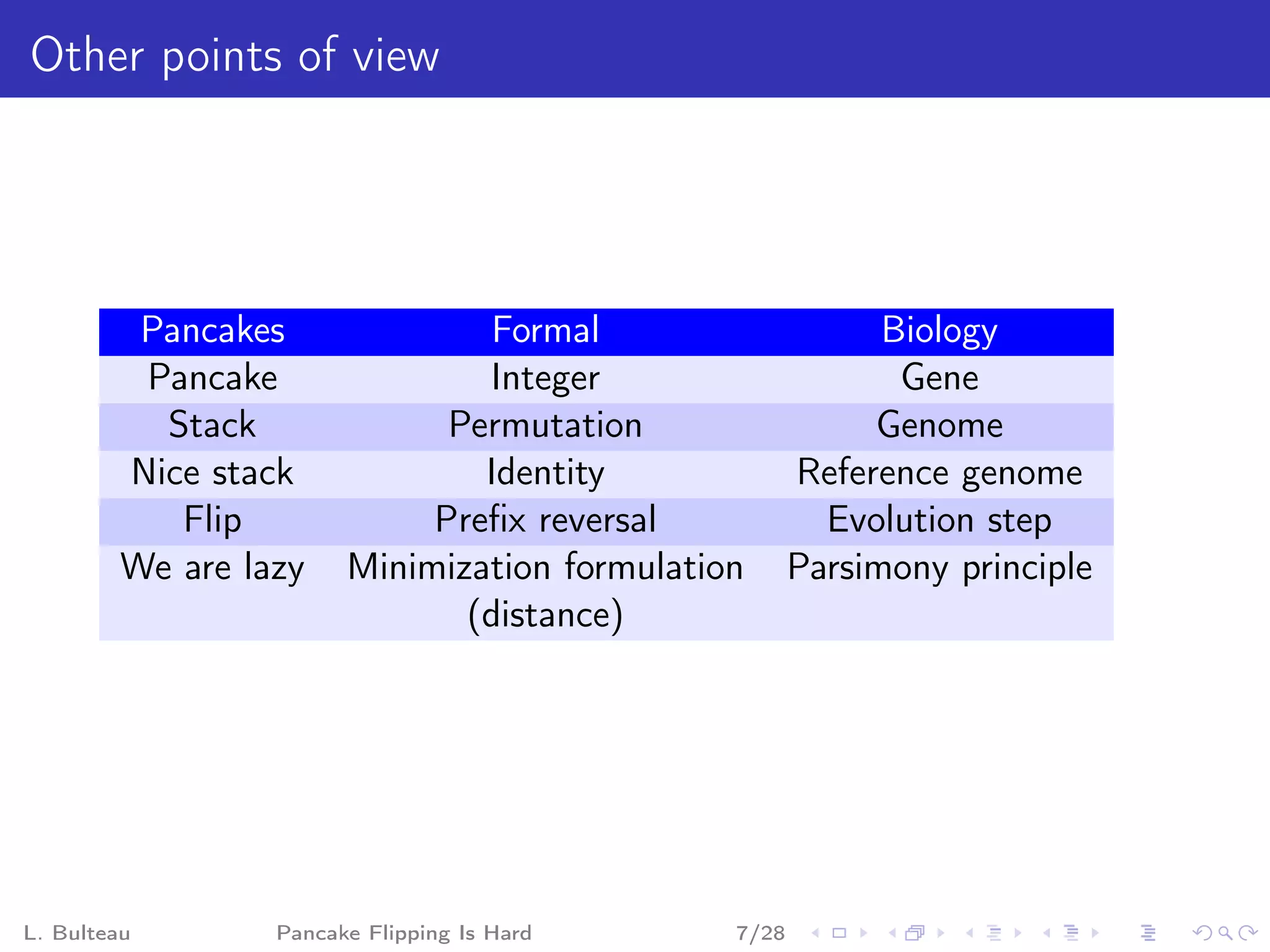
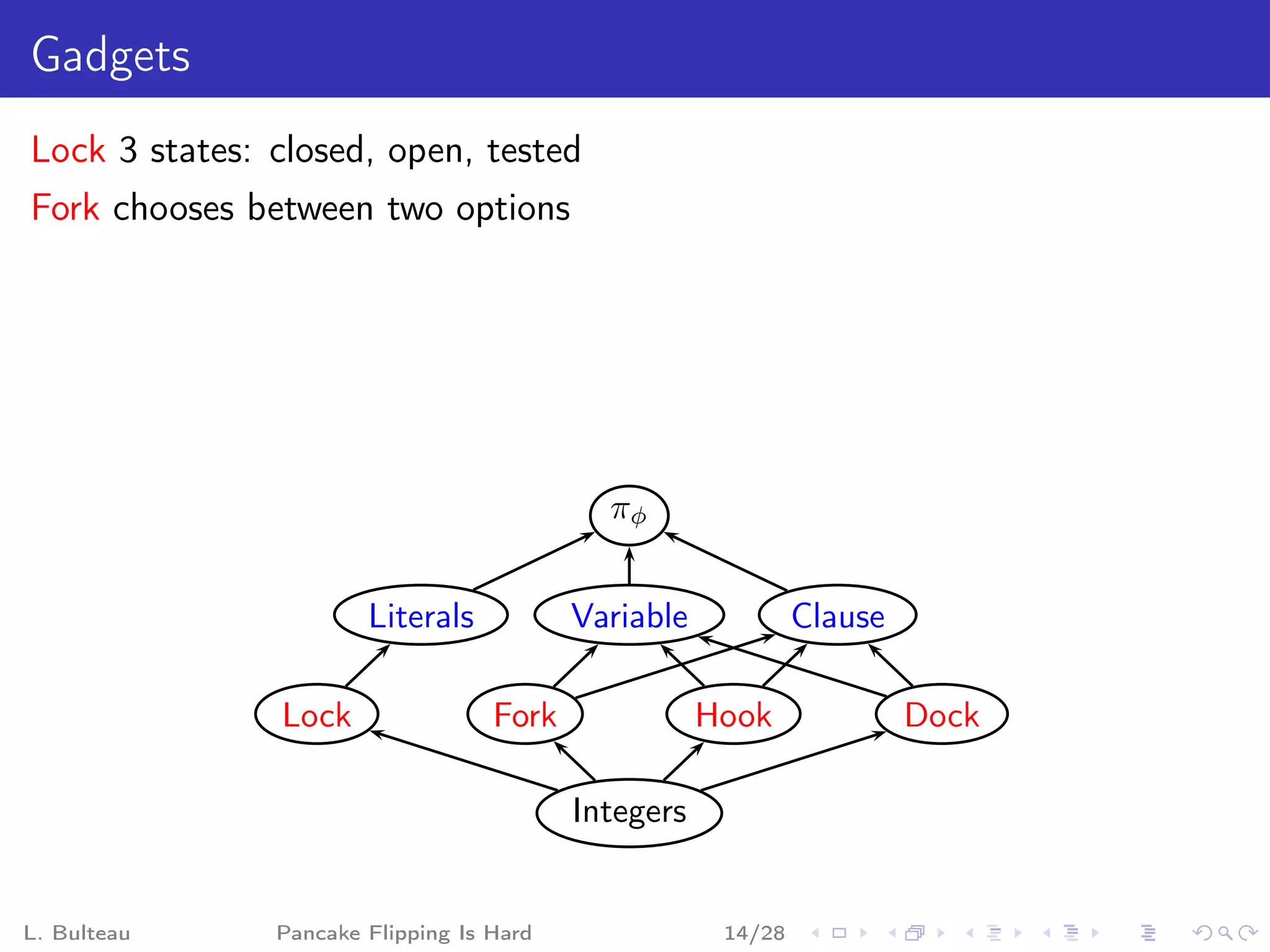
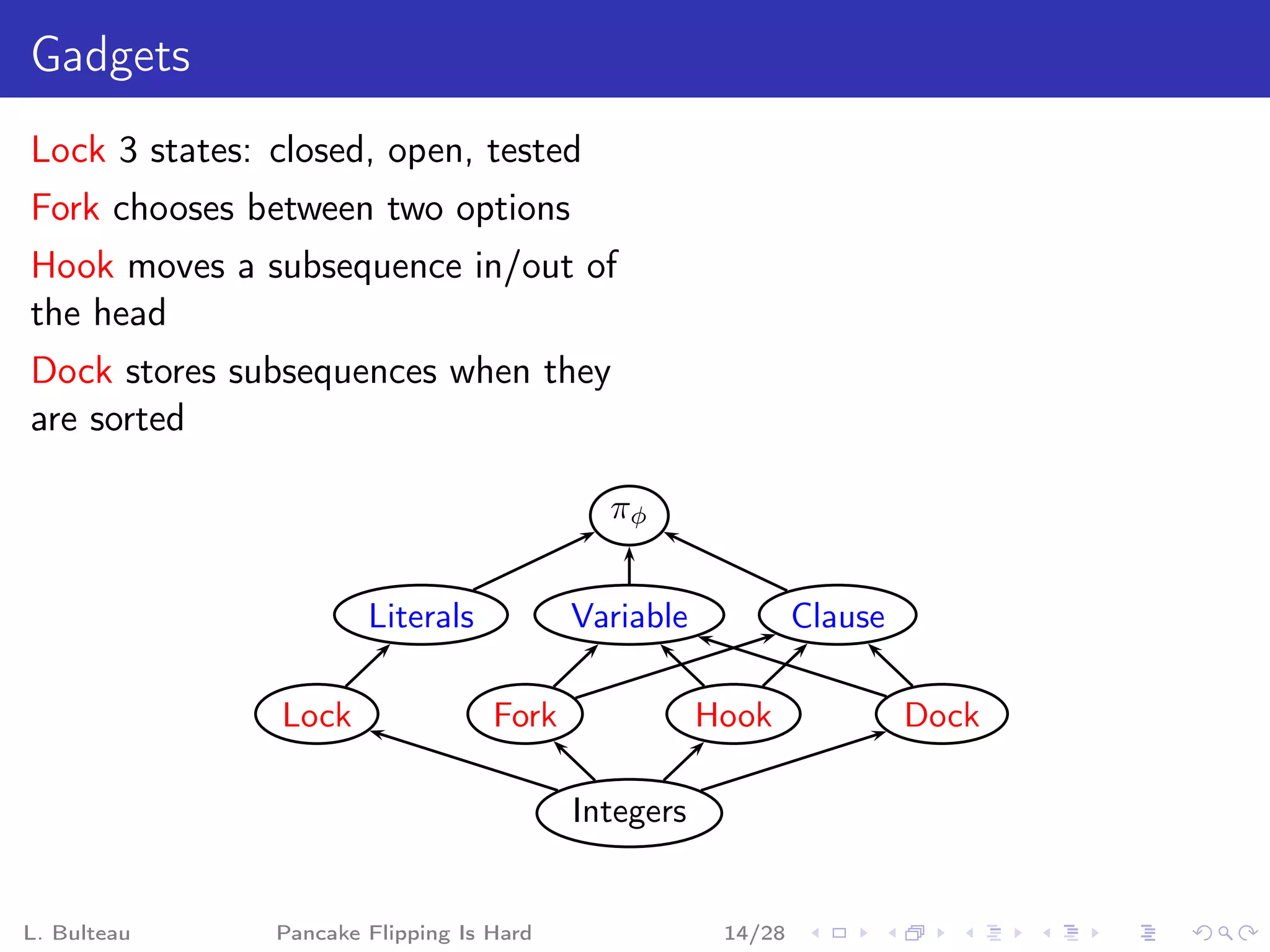
The document discusses the "pancake flipping problem" which involves rearranging a stack of pancakes of different sizes into a pyramidal stack with the fewest number of flips using a spatula. It presents this problem as analogous to problems in formal mathematics and biology, establishes that solving it is NP-complete, and provides details on known bounds and efficient flipping strategies as well as proposed "gadgets" to model the problem through a reduction from 3-SAT.

1. Pancake Flipping Is Hard
Laurent BULTEAU, Guillaume FERTIN, Irena RUSU
LINA, Université de Nantes
Feb. 21st, 2012

2. Pancake Flipping Problem
L. Bulteau Pancake Flipping Is Hard 2/28

3. Pancakes
we are given a stack of pancakes, all of different sizes
L. Bulteau Pancake Flipping Is Hard 3/28

4. Pancakes
we are given a stack of pancakes, all of different sizes
we want to rearrange it into a beautiful pyramidal stack
L. Bulteau Pancake Flipping Is Hard 3/28

5. Pancakes
we are given a stack of pancakes, all of different sizes
we want to rearrange it into a beautiful pyramidal stack
we have a spatula, to flip the top of the stack
L. Bulteau Pancake Flipping Is Hard 3/28

6. Pancakes
we are given a stack of pancakes, all of different sizes
we want to rearrange it into a beautiful pyramidal stack
we have a spatula, to flip the top of the stack
we are lazy
L. Bulteau Pancake Flipping Is Hard 3/28

7. Pancakes
Example
L. Bulteau Pancake Flipping Is Hard 4/28

8. Pancakes
Example
L. Bulteau Pancake Flipping Is Hard 4/28

9. Pancakes
Example
L. Bulteau Pancake Flipping Is Hard 4/28

10. Pancakes
Example
L. Bulteau Pancake Flipping Is Hard 4/28

11. Pancakes
Example
L. Bulteau Pancake Flipping Is Hard 4/28

12. Pancakes
Example
L. Bulteau Pancake Flipping Is Hard 4/28

13. Pancakes
Example
L. Bulteau Pancake Flipping Is Hard 4/28

14. Pancakes
Example
L. Bulteau Pancake Flipping Is Hard 4/28

15. Pancakes
Example
L. Bulteau Pancake Flipping Is Hard 4/28

16. Pancakes
Example
L. Bulteau Pancake Flipping Is Hard 4/28

17. Pancakes
Example
L. Bulteau Pancake Flipping Is Hard 4/28

18. Pancakes
Example
L. Bulteau Pancake Flipping Is Hard 4/28

19. Pancakes
Example
L. Bulteau Pancake Flipping Is Hard 4/28

20. Pancakes
Example
L. Bulteau Pancake Flipping Is Hard 4/28

21. Pancakes
Example
L. Bulteau Pancake Flipping Is Hard 4/28

22. Pancakes
Example
L. Bulteau Pancake Flipping Is Hard 4/28

23. Pancakes
Example
L. Bulteau Pancake Flipping Is Hard 4/28

24. The problem to be solved
Problem
Given a stack of n pancakes, how can it be arranged with as little
effort as possible?
L. Bulteau Pancake Flipping Is Hard 5/28

25. Other points of view
“Pancake view”
Given a stack of n pancakes, how can it be arranged with as little
effort as possible?
Formal problem : MIN-SBPR
Given a permutation π of {1, . . . , n}, compute the prefix reversal
distance between π and the Identity, written prd (π).
“Biology view”
Given two genomes using the same n genes, how many steps have
been used in evolution between one and the other?
L. Bulteau Pancake Flipping Is Hard 6/28

26. Other points of view
Pancakes Formal Biology
Pancake Integer Gene
Stack Permutation Genome
L. Bulteau Pancake Flipping Is Hard 7/28

27. Other points of view
Pancakes Formal Biology
Pancake Integer Gene
Stack Permutation Genome
Nice stack Identity Reference genome
Flip Prefix reversal Evolution step
L. Bulteau Pancake Flipping Is Hard 7/28

28. Other points of view
Pancakes Formal Biology
Pancake Integer Gene
Stack Permutation Genome
Nice stack Identity Reference genome
Flip Prefix reversal Evolution step
We are lazy Minimization formulation Parsimony principle
(distance)
L. Bulteau Pancake Flipping Is Hard 7/28

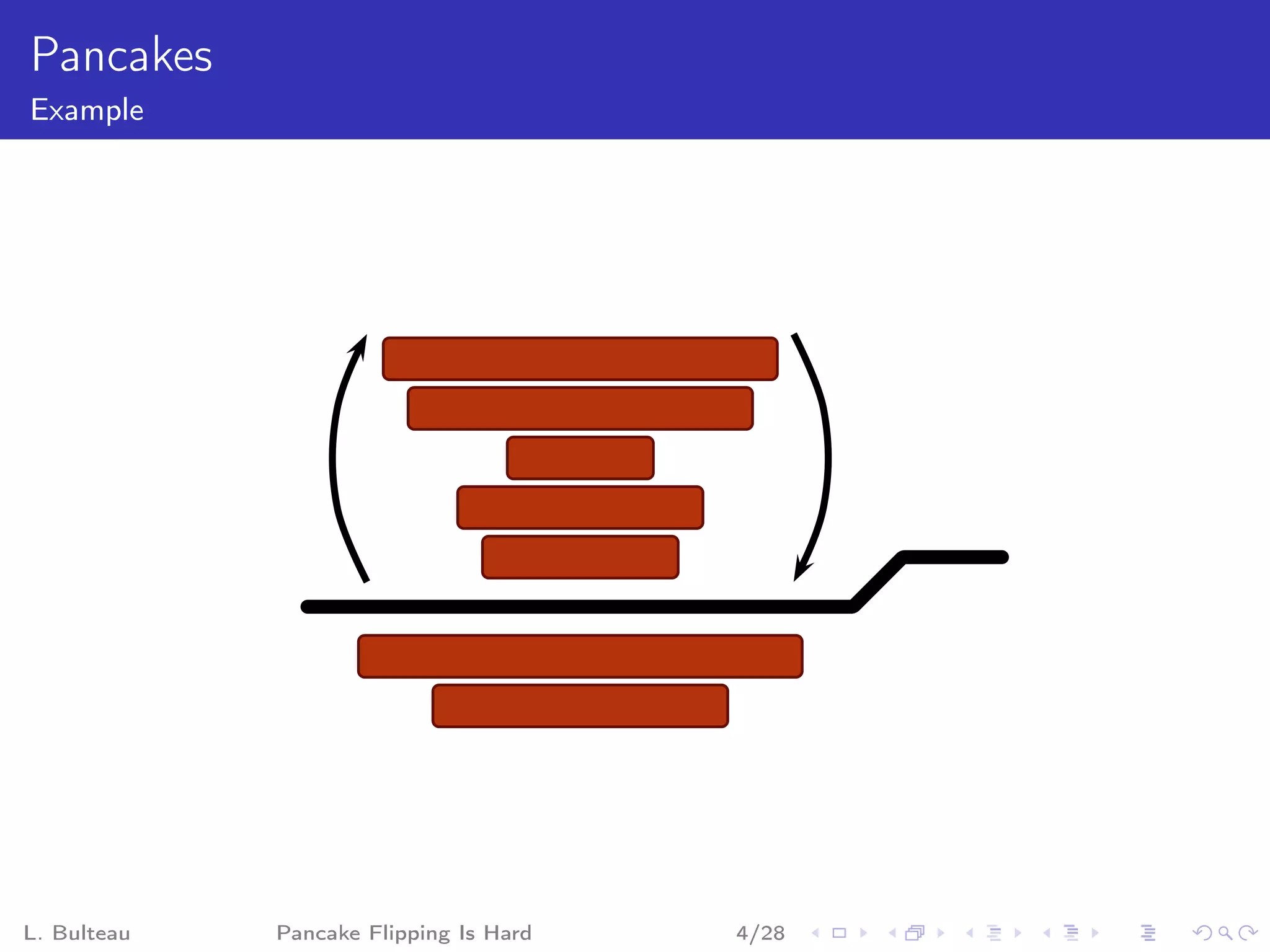
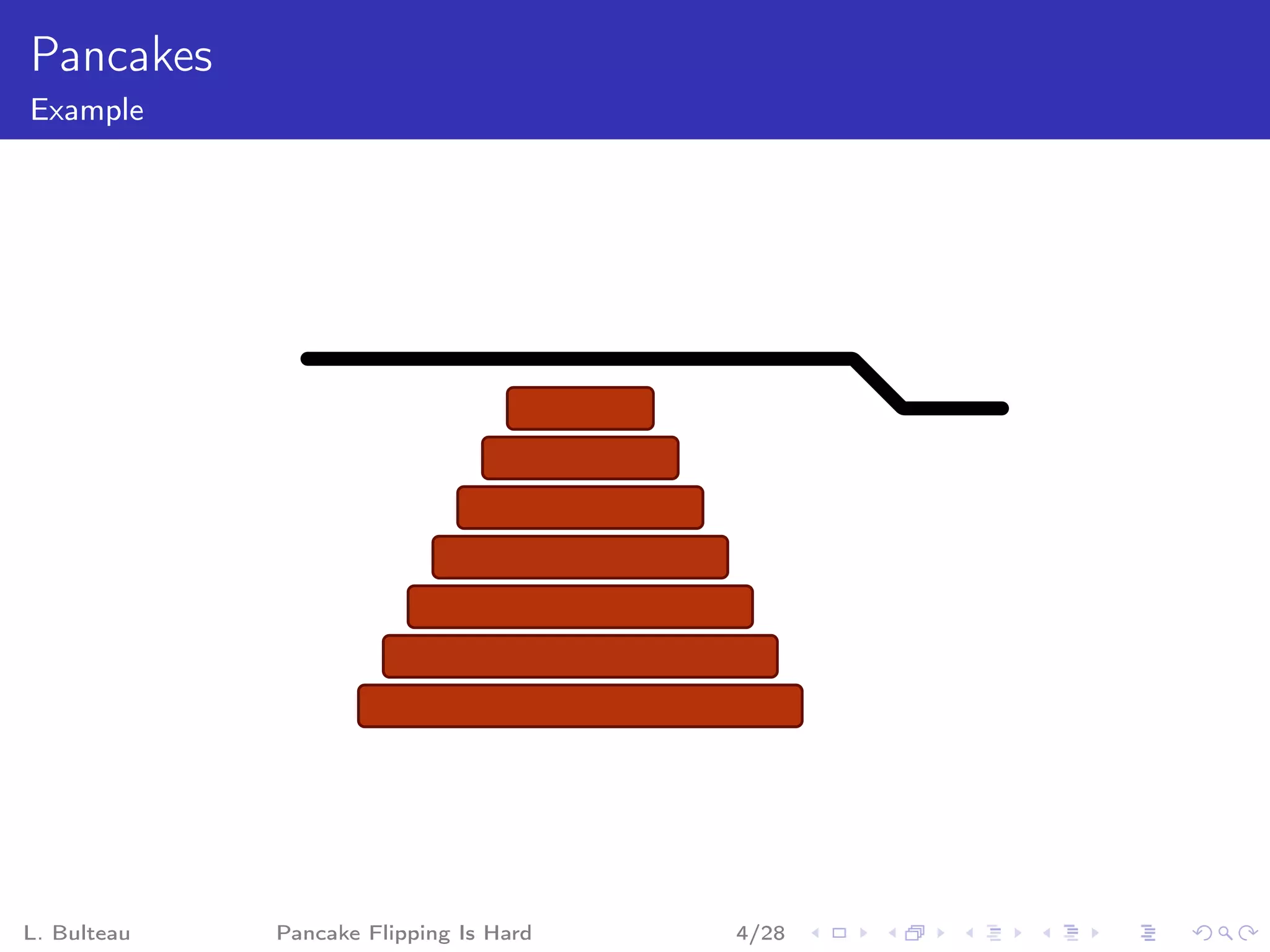
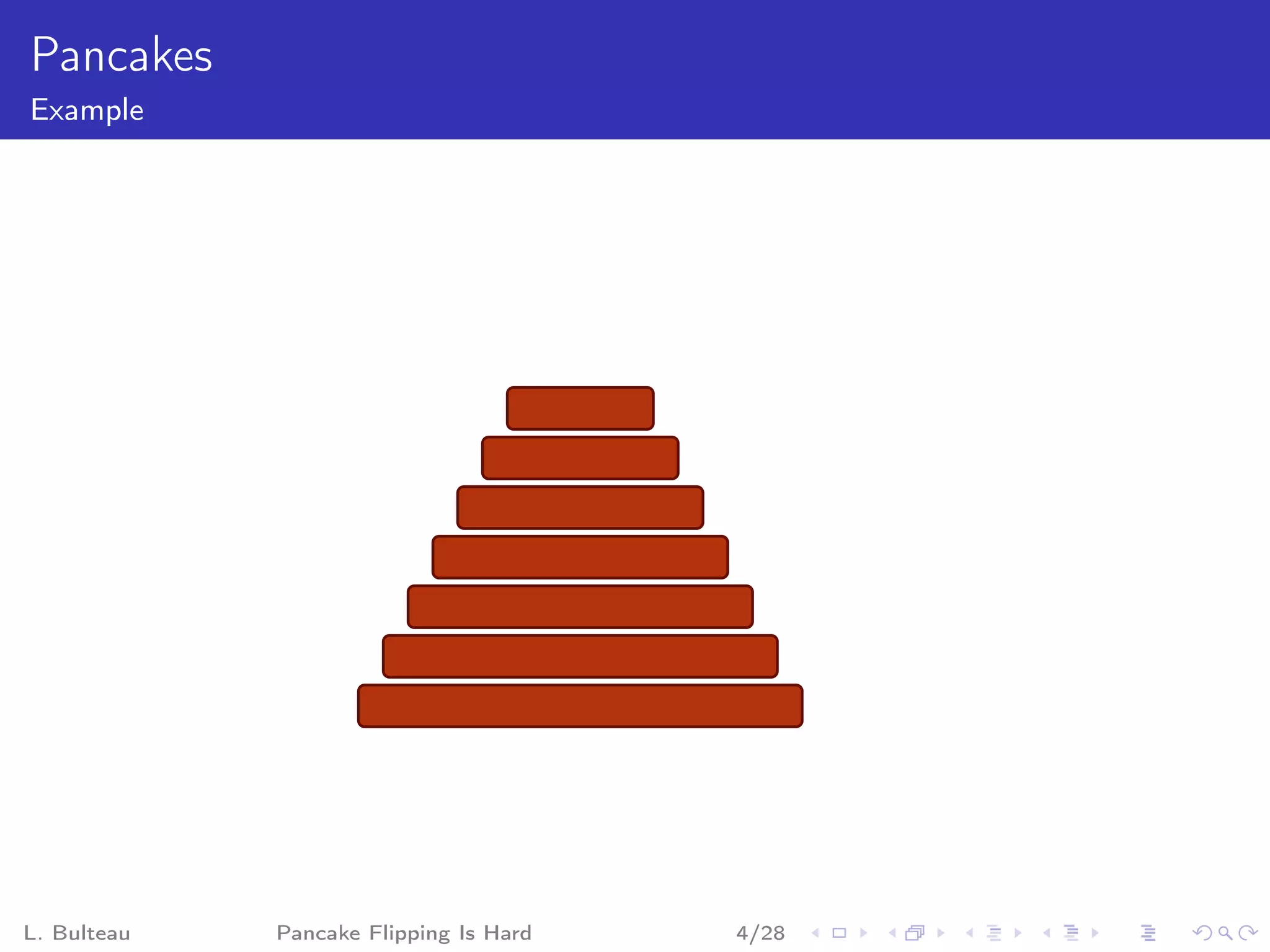
29. Pancake Problem
Complexity: NP-complete
Related results:
Reversal distance, not necessarily prefix:
NP-complete (APX-hard) for unsigned permutations,
polynomial for signed permutations.
Burnt pancakes variant, or Prefix Reversal Distance for signed
permutations:
complexity unknown.
Algorithms:
polynomial-time algorithm for a subclass of signed
permutations (simple permutations [Labarre, Cibulka, 2011])
2-approximation algorithm
L. Bulteau Pancake Flipping Is Hard 8/28

30. Known bounds
Upper bound
prd (π) ≤ 2(n − 1)
Repeat at most n − 1 times
Find the largest unsorted pancake, flip it to the top
Flip it back to its destination
At most 2(n − 1) flips to sort a stack.
L. Bulteau Pancake Flipping Is Hard 9/28

31. Known bounds
Upper bound
prd (π) ≤ 2(n − 1)
Anything better ?
L. Bulteau Pancake Flipping Is Hard 9/28

32. Known bounds
Upper bound
prd (π) ≤ 2(n − 1)
Anything better ? – Yes :
prd (π) ≤ (5n + 5)/3 [Gates & Papadimitriou, 1979]
L. Bulteau Pancake Flipping Is Hard 9/28

33. Known bounds
Upper bound
prd (π) ≤ 2(n − 1)
Anything better ? – Yes :
prd (π) ≤ (5n + 5)/3 [Gates & Papadimitriou, 1979]
prd (π) ≤ (18n)/11 + O(1) [Chitturi et al., 2009]
L. Bulteau Pancake Flipping Is Hard 9/28

34. Known bounds
Upper bound
prd (π) ≤ (18n)/11 + O(1) [Chitturi et al., 2009]
Lower bound
prd (π) ≥ db (π)
Breakpoint at position i if:
i < n and π(i + 1) = π(i) ± 1
i = n and π(n) = n
db (π) : number of breakpoints
L. Bulteau Pancake Flipping Is Hard 9/28

35. Known bounds
Upper bound
prd (π) ≤ (18n)/11 + O(1) [Chitturi et al., 2009]
Lower bound
prd (π) ≥ db (π)
Breakpoint at position i if:
i < n and π(i + 1) = π(i) ± 1
i = n and π(n) = n
db (π) : number of breakpoints
At most one breakpoint is removed with each flip
L. Bulteau Pancake Flipping Is Hard 9/28

36. Our result
Reduction from 3-SAT: from a formula φ, create a
permutation πφ such that prd (πφ ) = db (πφ ) iff φ is satisfiable.
Given a permutation π, deciding wether π can be sorted with
no more than db (π) flips is NP-hard.
MIN-SBPR is NP-hard (hence NP-complete)
L. Bulteau Pancake Flipping Is Hard 10/28

37. Reduction
L. Bulteau Pancake Flipping Is Hard 11/28

38. Efficient flips
A flip is efficient if it removes one breakpoint: π→π
prd (πφ ) = db (πφ ) iff there exists a “path” of efficient flips
from πφ to the Identity. πφ →∗ In
1
At most two efficient flips are possible from every permutation
h
.
.
.
x
h−1
.
.
.
y
h+1
.
.
.
L. Bulteau Pancake Flipping Is Hard 12/28

39. Efficient flips
A flip is efficient if it removes one breakpoint: π→π
prd (πφ ) = db (πφ ) iff there exists a “path” of efficient flips
from πφ to the Identity. πφ →∗ In
1
At most two efficient flips are possible from every permutation
h
x .
. y
.
.
. .
.
. x .
h h−1 h−1
h−1 .
. x
.
.
. .
.
. y .
y h+1 h
h+1 .
. h+1
.
.
. .
.
. .
L. Bulteau Pancake Flipping Is Hard 12/28

40. Efficient flips
A flip is efficient if it removes one breakpoint: π→π
prd (πφ ) = db (πφ ) iff there exists a “path” of efficient flips
from πφ to the Identity. πφ →∗ In
1
At most two efficient flips are possible from every permutation
h
x .
. y
.
.
. .
.
. x =h−2 .
h h−1 h−1
h−1 X .
.
. x
.
. .
.
. y .
y h+1 h
h+1 .
. h+1
.
.
. .
.
. .
L. Bulteau Pancake Flipping Is Hard 12/28

41. Efficient flips
A flip is efficient if it removes one breakpoint: π→π
prd (πφ ) = db (πφ ) iff there exists a “path” of efficient flips
from πφ to the Identity. πφ →∗ In
1
At most two efficient flips are possible from every permutation
h
x .
. y
.
.
. .
.
. x .
h h−1 h−1
h−1 .
. X x
.
.
. .
.
. y =h+2 .
y h+1 h
h+1 .
. h+1
.
.
. .
.
. .
L. Bulteau Pancake Flipping Is Hard 12/28

42. Efficient flips
A flip is efficient if it removes one breakpoint: π→π
prd (πφ ) = db (πφ ) iff there exists a “path” of efficient flips
from πφ to the Identity. πφ →∗ In
1
At most two efficient flips are possible from every permutation
h
x .
. y
.
.
. .
.
. x =h−2 .
h h−1 h−1
h−1 X .
.
.
X x
.
. .
.
. y =h+2 .
y h+1 h
h+1 .
. h+1
.
.
. .
.
. .
L. Bulteau Pancake Flipping Is Hard 12/28

43. Reduction ideas
Create πφ in order to know precisely which efficient flips are
possible (from πφ or subsequent permutations)
One possible flip: usual case, there is one path to follow
Two possible flips: a choice has to be made
e.g., assigning “true” or “false” to a variable
No possible flip: bad choices have been made
e.g., a clause is unsatisfied
Necessity to end with the Identity permutation.
L. Bulteau Pancake Flipping Is Hard 13/28

44. Gadgets
Lock 3 states: closed, open, tested
πφ
Literals Variable Clause
Lock Fork Hook Dock
Integers
L. Bulteau Pancake Flipping Is Hard 14/28

45. Gadgets
Lock 3 states: closed, open, tested
Fork chooses between two options
πφ
Literals Variable Clause
Lock Fork Hook Dock
Integers
L. Bulteau Pancake Flipping Is Hard 14/28

46. Gadgets
Lock 3 states: closed, open, tested
Fork chooses between two options
Hook moves a subsequence in/out of
the head
πφ
Literals Variable Clause
Lock Fork Hook Dock
Integers
L. Bulteau Pancake Flipping Is Hard 14/28

47. Gadgets
Lock 3 states: closed, open, tested
Fork chooses between two options
Hook moves a subsequence in/out of
the head
Dock stores subsequences when they
are sorted
πφ
Literals Variable Clause
Lock Fork Hook Dock
Integers
L. Bulteau Pancake Flipping Is Hard 14/28

48. Gadgets
Lock 3 states: closed, open, tested Literals holds a lock for each literal
Fork chooses between two options in the formula
Hook moves a subsequence in/out of
the head
Dock stores subsequences when they
are sorted
πφ
Literals Variable Clause
Lock Fork Hook Dock
Integers
L. Bulteau Pancake Flipping Is Hard 14/28

49. Gadgets
Lock 3 states: closed, open, tested Literals holds a lock for each literal
Fork chooses between two options in the formula
Hook moves a subsequence in/out of Variable opens locks corresponding
the head to either x or ¬x
Dock stores subsequences when they
are sorted
πφ
Literals Variable Clause
Lock Fork Hook Dock
Integers
L. Bulteau Pancake Flipping Is Hard 14/28

50. Gadgets
Lock 3 states: closed, open, tested Literals holds a lock for each literal
Fork chooses between two options in the formula
Hook moves a subsequence in/out of Variable opens locks corresponding
the head to either x or ¬x
Dock stores subsequences when they
Clause tests one lock out of three
are sorted
πφ
Literals Variable Clause
Lock Fork Hook Dock
Integers
L. Bulteau Pancake Flipping Is Hard 14/28

51. Lock gadget
Lock gadget (closed)
1
2
9
8
5
L=
6
4
3
11
12
key = 10
test = 7
L. Bulteau Pancake Flipping Is Hard 15/28

52. Lock gadget
Lock gadget (closed) Open
1 1
2 2
9 3
8 4
5 6
L=
6 Lo = 5
4 8
3 9
11 10
12 11
12
key = 10
test = 7
L. Bulteau Pancake Flipping Is Hard 15/28

53. Lock gadget
Lock gadget (closed) Open Tested
1 1 1
2 2 2
9 3 3
8 4 4
5 6 5
L=
6 Lo = 5 6
1
4 8 I12 =
7
3 9 8
11 10 9
12 11 10
12 11
key = 10 12
test = 7
L. Bulteau Pancake Flipping Is Hard 15/28

54. Lock gadget
Lock gadget (closed) Open Tested
p+1 p+1 p+1
p+2 p+2 p+2
p+9 p+3 p+3
p+8 p+4 p+4
p+5 p+6 p+5
L=
p+6 Lo = p + 5 p+1 p+6
p+4 p+8 Ip+12 =
p+7
p+3 p+9 p+8
p + 11 p + 10 p+9
p + 12 p + 11 p + 10
p + 12 p + 11
key = p + 10 p + 12
test = p + 7
L. Bulteau Pancake Flipping Is Hard 15/28

55. Lock gadget
Lock gadget (closed) Open Tested
1 1 1
2 2 2
9 3 3
8 4 4
5 6 5
L=
6 Lo = 5 6
1
4 8 I12 =
7
3 9 8
11 10 9
12 11 10
12 11
key = 10 12
test = 7
L. Bulteau Pancake Flipping Is Hard 15/28

56. Lock gadget
key .
. .
.
.
.
Opening →∗ Lo
L .
. .
.
.
.
test .
. .
.
Testing .
.
→∗ 1
I12
(when open) Lo .
. .
.
.
.
test
.
.
Testing .
→∗ ∅
(when closed) L
.
.
.
L. Bulteau Pancake Flipping Is Hard 16/28

57. Lock gadget
key
X
X
Opening →∗ Lo
L
Y
Y
test
X
Testing X
→∗ 1
I12
(when open) Lo
Y
Y
test
Testing X
→∗ ∅
(when closed) L
Y
L. Bulteau Pancake Flipping Is Hard 16/28

58. Lock gadget
key 10
X X
L 1
Y 2
9
8
5
6
4
3
11
12
Y
L. Bulteau Pancake Flipping Is Hard 17/28

59. Lock gadget
key 10
X X
2 3
L 1
1 4
Y 2
X 6
9
10 5
8
9 8
5
8 9
6
5 2
4
6 1
3
4 X
11
3 10
12
11 11
Y
12 12
Y Y
L. Bulteau Pancake Flipping Is Hard 17/28

60. Lock gadget
key 10
X X
2 3
L 1
1 4
Y 2
X 6
9
10 5
8
9 8
5
8 9
6
5 2
4
6 1
∅ 3
4 X
11
3 10
12
11 11
Y
12 12
Y Y
L. Bulteau Pancake Flipping Is Hard 17/28

61. Lock gadget
key 10
X X
2 3
L 1
1 4
Y 2 9
X 6
9 8
10 5
8 5
9 8
5 6
8 9
6 4
5 2
4 3
6 1
∅ 3 2
4 X
11 1
3 10
12 X
11 11
Y 10
12 12
11
Y Y
12
Y
L. Bulteau Pancake Flipping Is Hard 17/28

62. Lock gadget
key 10
X X
2 3
L 1
1 4
Y 2 9
X 6
9 8
10 5 X
8 5
9 8 1
5 6
8 9 2
6 4
5 2 3
4 3
6 1 4
∅ 3 2
4 X 6 X
11 1
3 10 5 = Lo
12 X
11 11 8 Y
Y 10
12 12 9
11
Y Y 10
12
11
Y
12
Y
L. Bulteau Pancake Flipping Is Hard 17/28

63. Lock gadget
test
X 7
L X
Y 1
2
9
8
5 →∅
6
4
3
11
12
Y
L. Bulteau Pancake Flipping Is Hard 18/28

64. Lock gadget
test 7
X 4 X 5
Lo 3 1 6 6
Y 2 2 4 5 X
1 3 3 4 1
X 4 2 3 2
7 6 1 2 3
6 5 X 1 4
5 8 7 X 5
∅ X
8 9 8 7 6 1
= I12
9 10 9 8 7
Y
10 11 10 9 8
11 12 11 10 9
12 Y 12 11 10
Y Y 12 11
Y 12
Y
L. Bulteau Pancake Flipping Is Hard 19/28

65. Overall flow
Literals
xi : set Pi Open remaining
Open locks in P1 Open locks in N1
locks in P1 ∪ N1
¬xi : set Ni
. . . .
Clause Cj .
. .
. .
. .
.
aj ∨ bj ∨ cj
Open remaining
Open locks in Pl Open locks in Nl
locks in Pl ∪ Nl
Test remaining
Test lock a1 Test lock b1 Test lock c1
locks in {a1 , b1 , c1 }
.
. .
. .
. .
.
. . . .
Test remaining
Test lock ak Test lock bk Test lock ck
locks in {ak , bk , ck }
I
L. Bulteau Pancake Flipping Is Hard 20/28

66. Fork gadget
11
8
E=
7
3
10
9
6
12
13
F = 4
5
15
14
2
1
L. Bulteau Pancake Flipping Is Hard 21/28

67. Fork gadget
11 10 3
8 9 7
E=
7 6 8
3 7 11
8 10
10 11 9
9 12 6
1 2
6 F = 13 F = 12
12 14 13
13 15 4
F = 4 5 5
5 4 15
15 3 14
14 2 2
2 1 1
1
L. Bulteau Pancake Flipping Is Hard 21/28

68. Fork gadget
11
8
E=
7
3
10
9 . .
6 F1 = .
. F2 = .
.
12
13
F = 4
5
15
14
2
1
L. Bulteau Pancake Flipping Is Hard 21/28

69. Fork gadget
11 Two efficient paths
8
E=
7 E
3 X
X ∗ ∗
X
F
F1 . F2
10 . .
. .
.
. .
.
9 . .
6 F1 = .
. F2 = .
.
12 F1 ∗
I151
. →
. .
.
13 . .
F = 4
5 F2 I151
∗
15 . →
. .
.
. .
14
2
1
L. Bulteau Pancake Flipping Is Hard 21/28

70. Hook gadget
3
G=
4
12
11
6
5
H=
9
8
2
1
take = 10
put = 7
L. Bulteau Pancake Flipping Is Hard 22/28

71. Hook gadget
.
G=
3 G = .
.
4
.
H = .
.
12 .
11 G = .
.
6 .
5 H = .
.
H=
9
8
2
1
take = 10
put = 7
L. Bulteau Pancake Flipping Is Hard 22/28

72. Hook gadget
. Moves a substring up and down
G=
3 G = .
.
4
.
H = .
.
12 take put .
. X .
11 G = .
. .
.
. X .
G G
6 . G . G
H = .
. →∗ .
. . →∗ X
5 X .
.
H= H H
9 H H
8 .
. .
.
.
. . .
. .
2 . .
1
G
take = 10 X
X 1
∗ I12
put = 7 H → .
. .
.
.
.
L. Bulteau Pancake Flipping Is Hard 22/28

73. Dock gadget
1
2
Dock(2, 7) =
8
9
L. Bulteau Pancake Flipping Is Hard 23/28

74. Dock gadget
1 Stores a sorted substring ( I) out of the
2 head of the stack.
Dock(2, 7) =
8 3
I7 .
9 . .
. .
.
→∗ I91
Dock(2, 7) .
. .
.
.
.
L. Bulteau Pancake Flipping Is Hard 23/28

75. Variable gadget
take
Variable gadget
1 First part Move up the main sequence .
.
.
G
E
keyp1 Hook
.
. Fork
.
keypq
put
keyn1
.
.
.
keynq′
F
H
.
.
.
Dock
L. Bulteau Pancake Flipping Is Hard 24/28

76. Variable gadget
E
Variable gadget keyp1
1 First part Move up the main sequence .
.
. Fork
2 Choose between xi and ¬xi keypq
put
keyn1
.
.
.
keynq′
F
G′
.
.
. Hook
H′
.
.
.
Dock
L. Bulteau Pancake Flipping Is Hard 24/28

77. Variable gadget
keynq′
Variable gadget .
.
.
1 First part Move up the main sequence
keyn1
2 Choose between xi and ¬xi put
3 Open locks in Ni keypq
.
.
.
keyp1
F2
G′
.
.
. Hook
H′
.
.
.
Dock
L. Bulteau Pancake Flipping Is Hard 24/28

78. Variable gadget
put
Variable gadget keyn1
1 First part Move up the main sequence .
.
.
2 Choose between xi and ¬xi keynq′
3 Open locks in Ni F2
G′
4 Put back main sequence
. Hook
.
.
H′
.
.
.
Dock
L. Bulteau Pancake Flipping Is Hard 24/28

79. Variable gadget
Variable gadget
.
.
1 First part Move up the main sequence .
2 Choose between xi and ¬xi
G ′′
3 Open locks in Ni keyn1 Hook
4 Put back main sequence .
.
.
5 Other gadgets are activated keynq′
F2
H ′′
.
.
.
Dock
L. Bulteau Pancake Flipping Is Hard 24/28

80. Variable gadget
Variable gadget
G ′′
1 First part Move up the main sequence keyn1
2 Choose between xi and ¬xi .
. Hook
.
3 Open locks in Ni keynq′
4 Put back main sequence F2
H ′′
5 Other gadgets are activated .
.
.
6 Second part Hook collapses
Dock
L. Bulteau Pancake Flipping Is Hard 24/28

81. Variable gadget
Variable gadget keyn1
1 First part Move up the main sequence .
.
.
2 Choose between xi and ¬xi keynq′
F2
3 Open locks in Ni ⋆I
4 Put back main sequence .
.
.
5 Other gadgets are activated Dock
6 Second part Hook collapses
7 Open locks in Pi
L. Bulteau Pancake Flipping Is Hard 24/28

82. Variable gadget
Variable gadget F2
1 First part Move up the main sequence ⋆
I
.
.
2 Choose between xi and ¬xi .
3 Open locks in Ni Dock
4 Put back main sequence
5 Other gadgets are activated
6 Second part Hook collapses
7 Open locks in Pi
8 Fork collapses
L. Bulteau Pancake Flipping Is Hard 24/28

83. Variable gadget
Variable gadget ⋆
I
1 First part Move up the main sequence ⋆
I
.
.
2 Choose between xi and ¬xi .
3 Open locks in Ni Dock
4 Put back main sequence
5 Other gadgets are activated
6 Second part Hook collapses
7 Open locks in Pi
8 Fork collapses
9 Dock stores sorted sequences
L. Bulteau Pancake Flipping Is Hard 24/28

84. Variable gadget
Variable gadget .
.
.
1 First part Move up the main sequence
I
2 Choose between xi and ¬xi
3 Open locks in Ni
4 Put back main sequence
5 Other gadgets are activated
6 Second part Hook collapses
7 Open locks in Pi
8 Fork collapses
9 Dock stores sorted sequences
10 End Gadget sorted
L. Bulteau Pancake Flipping Is Hard 24/28

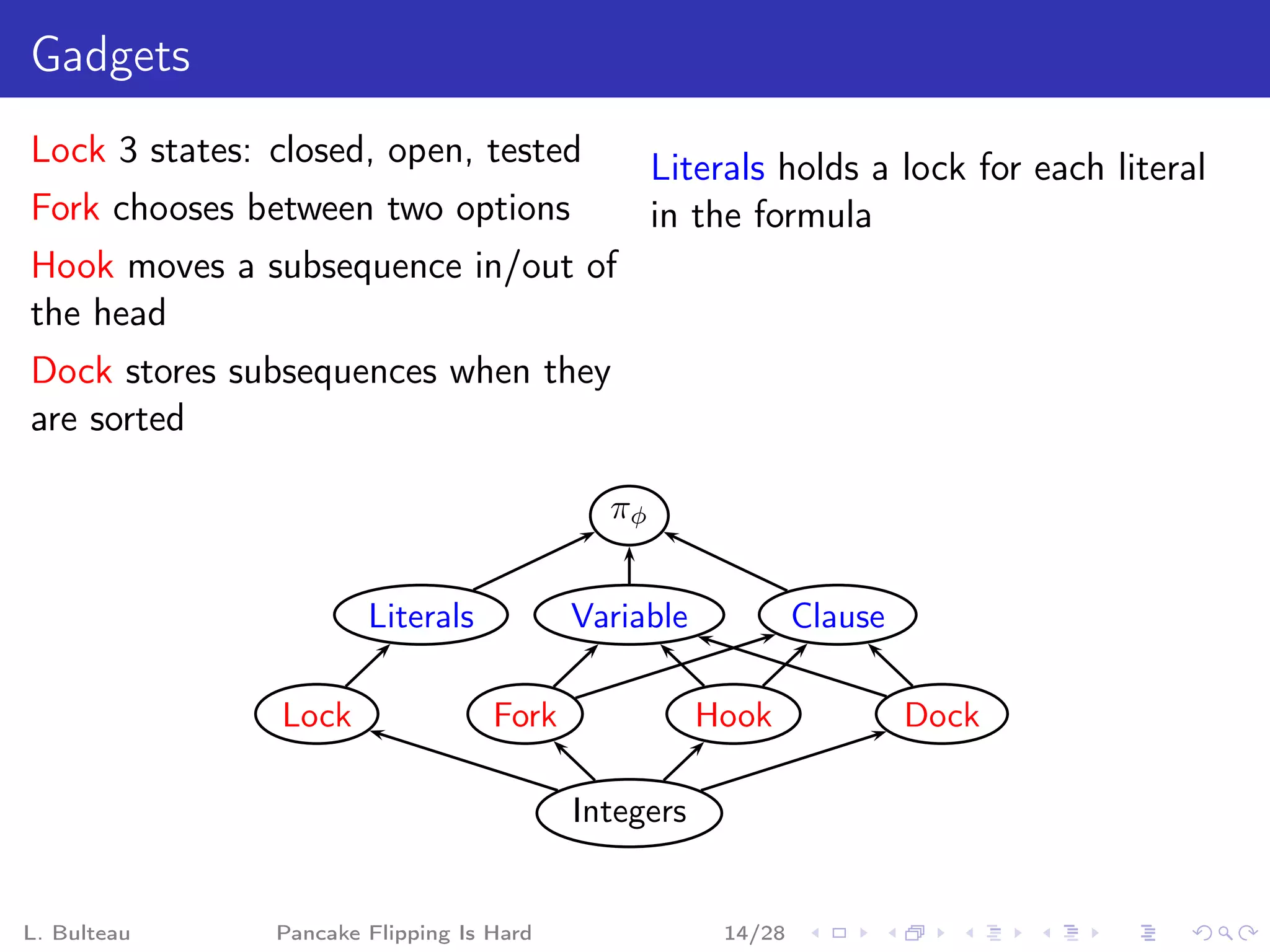
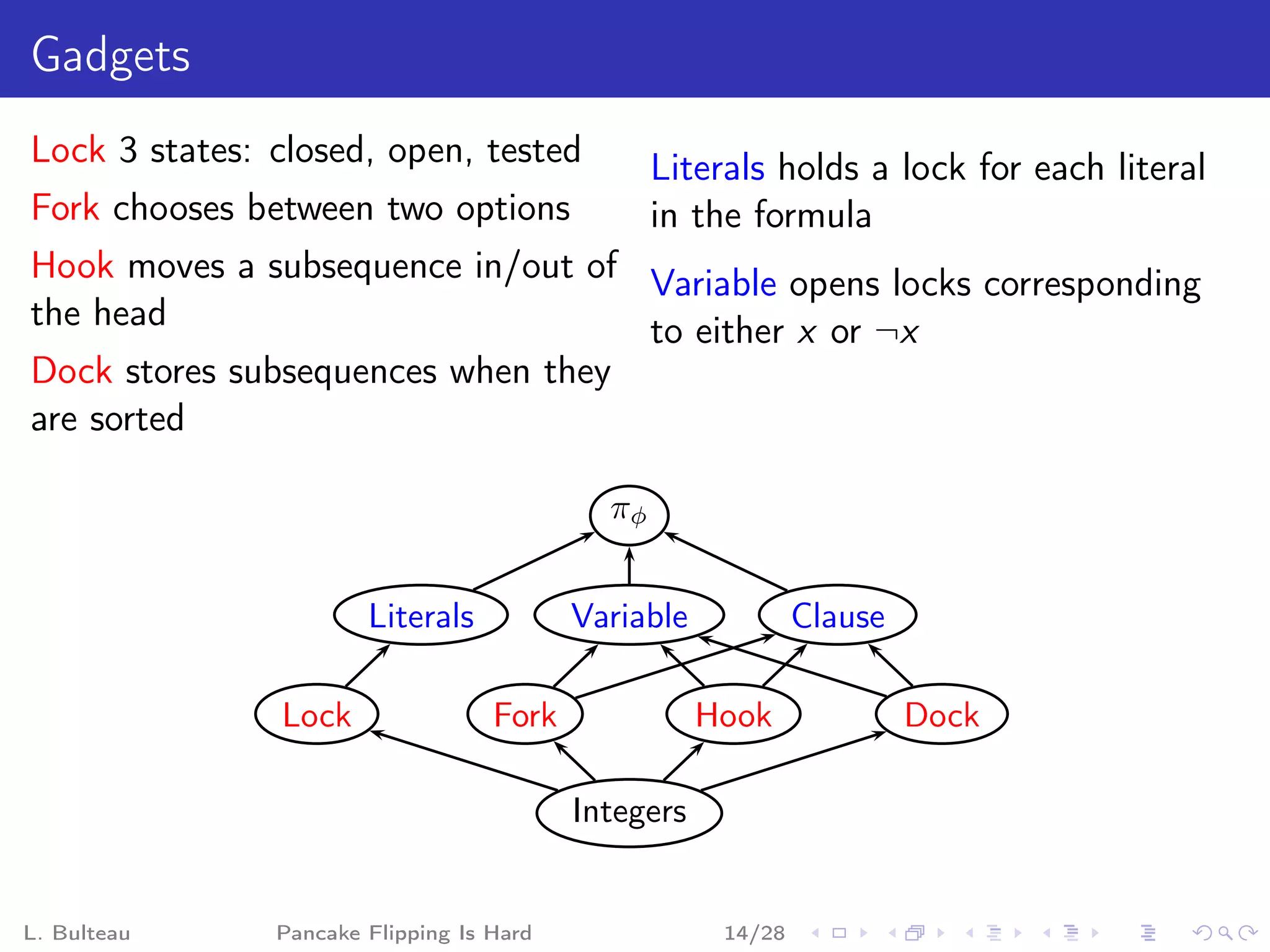
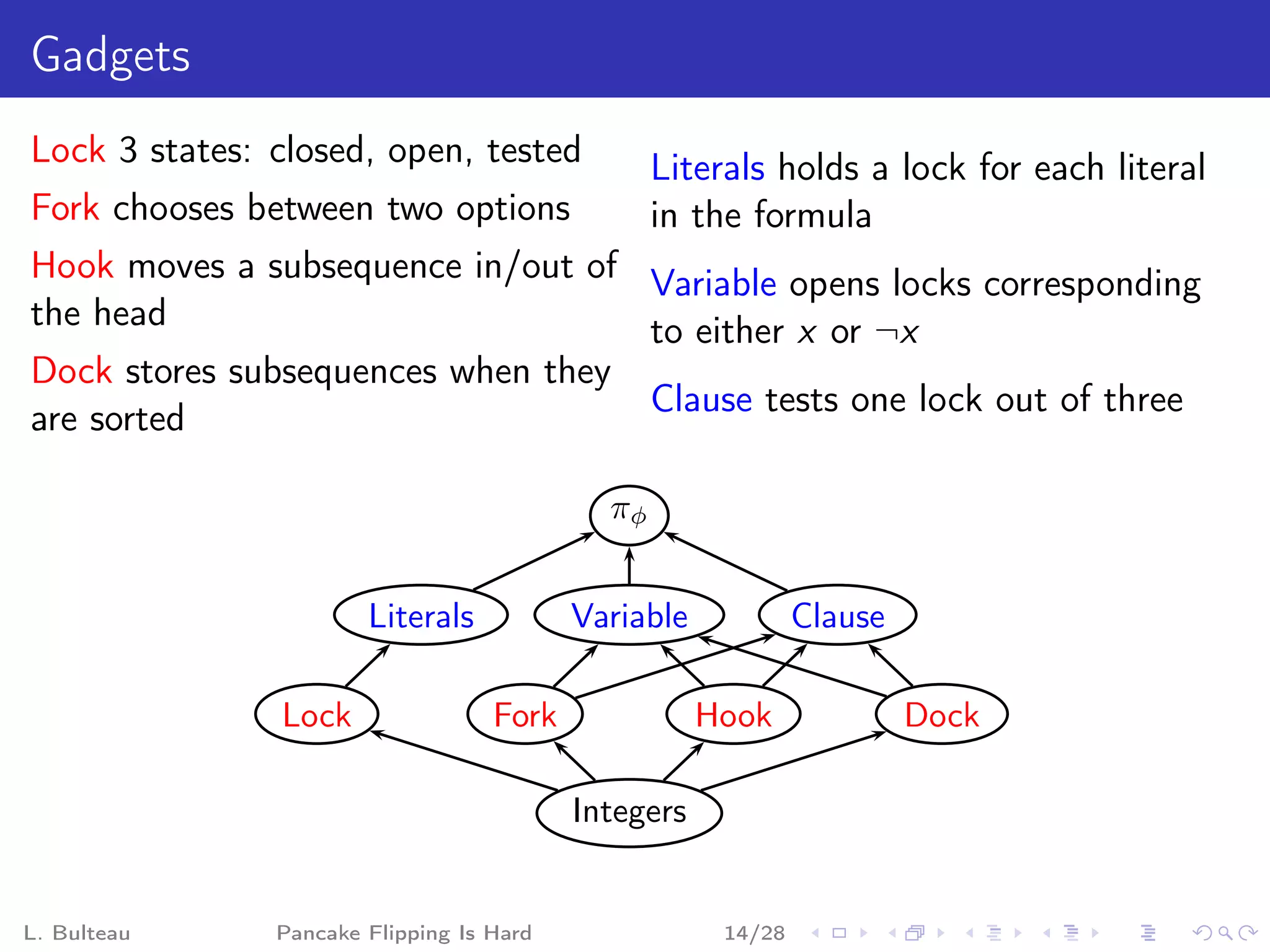
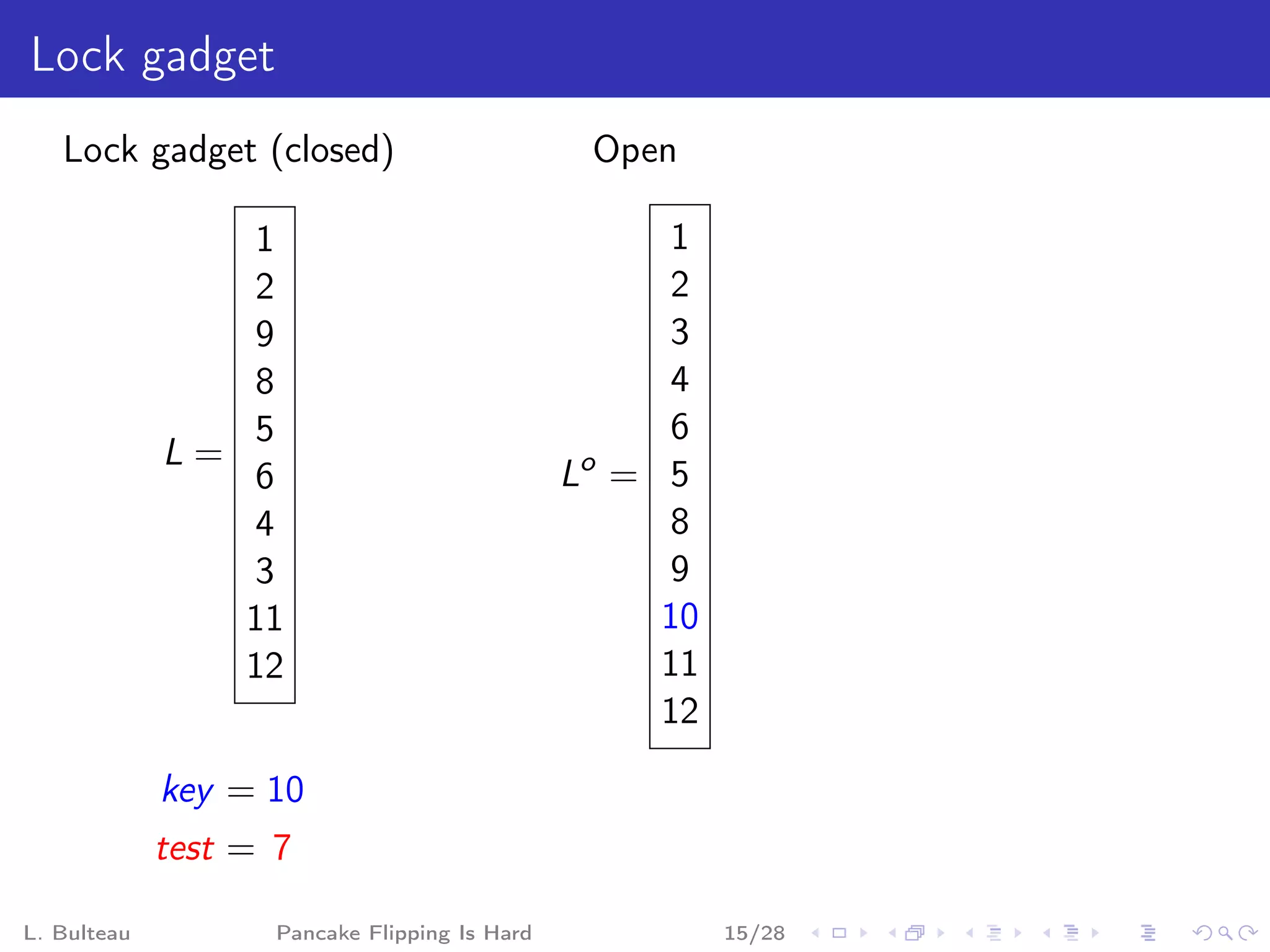
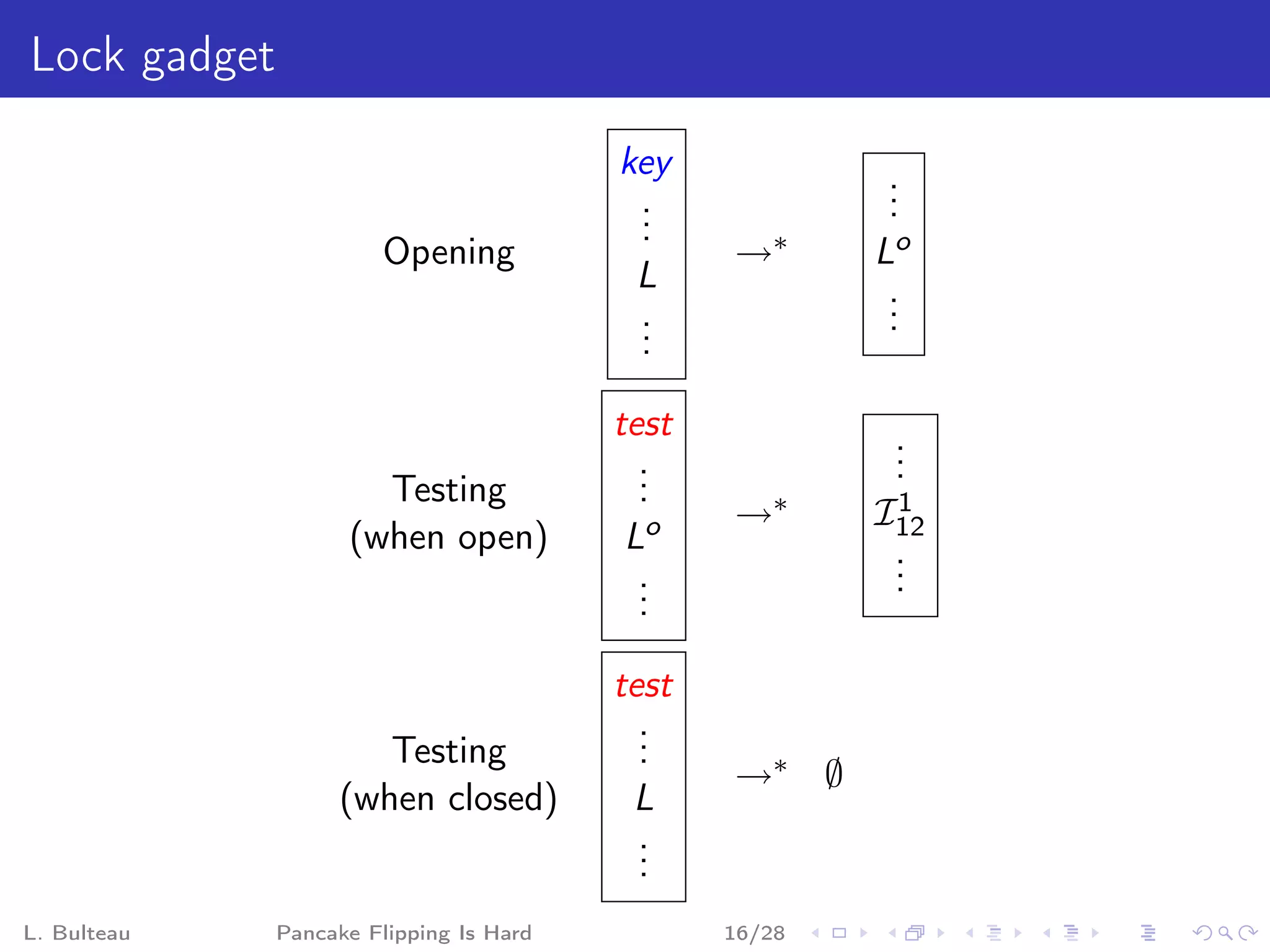
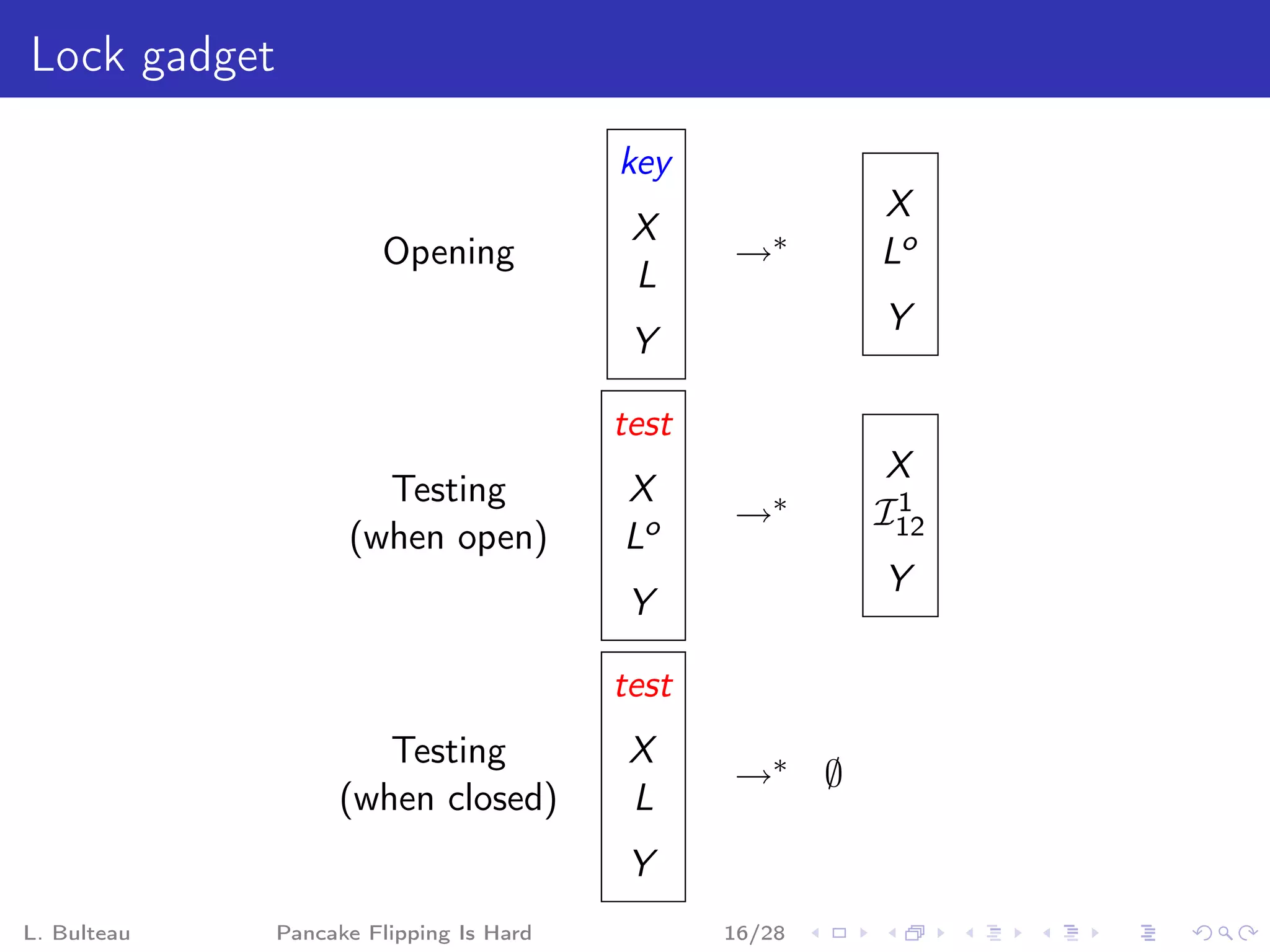
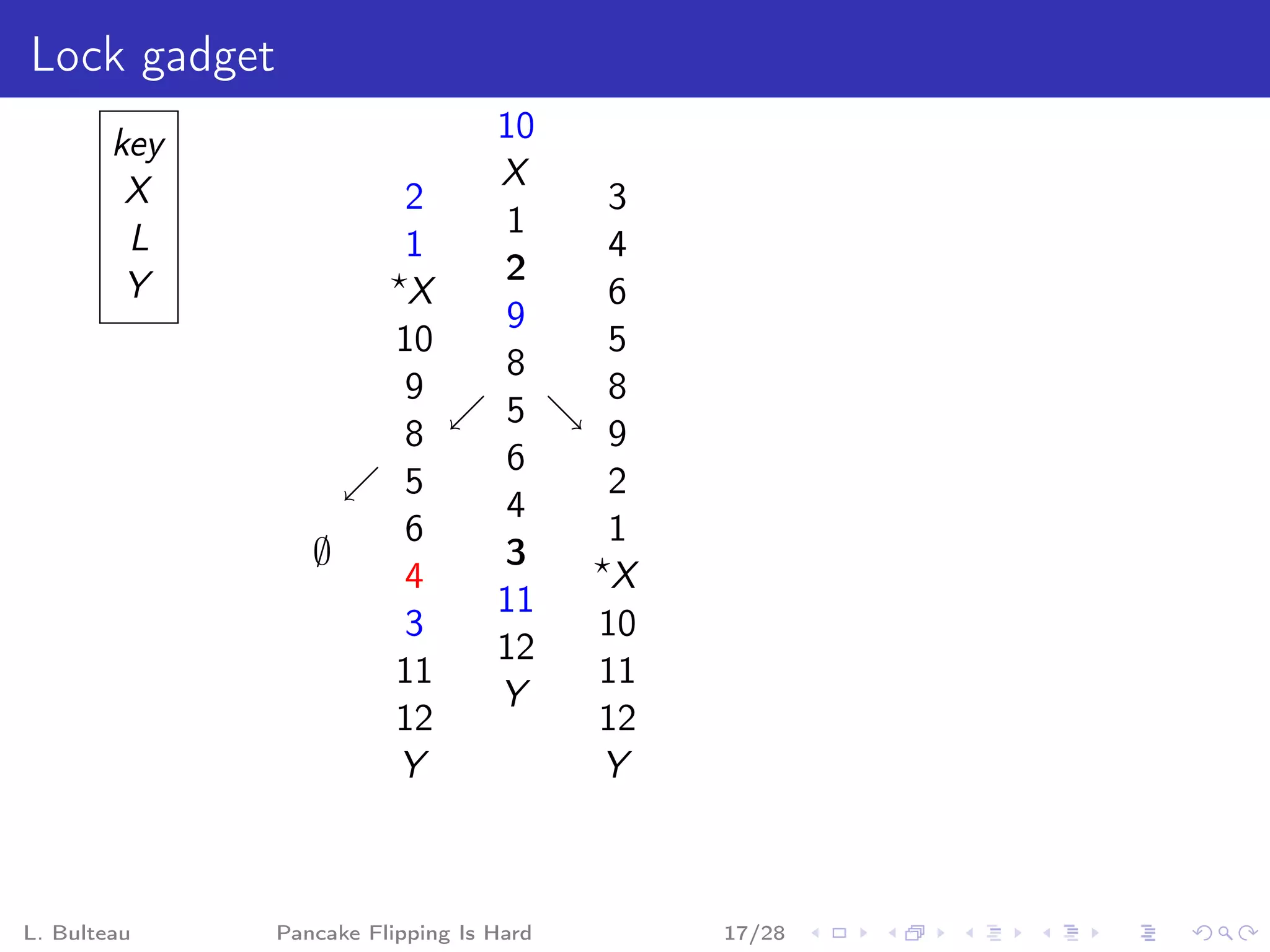
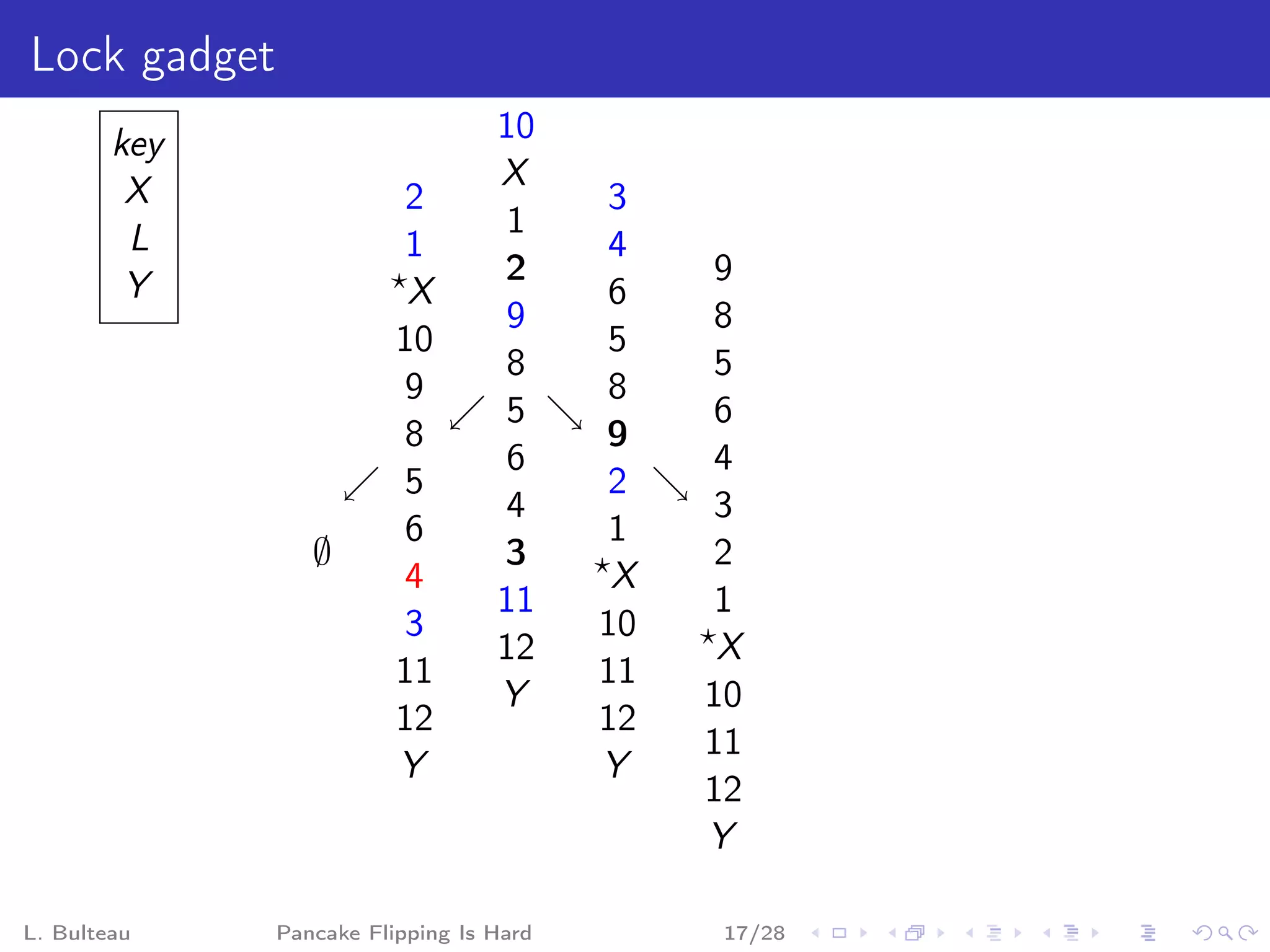
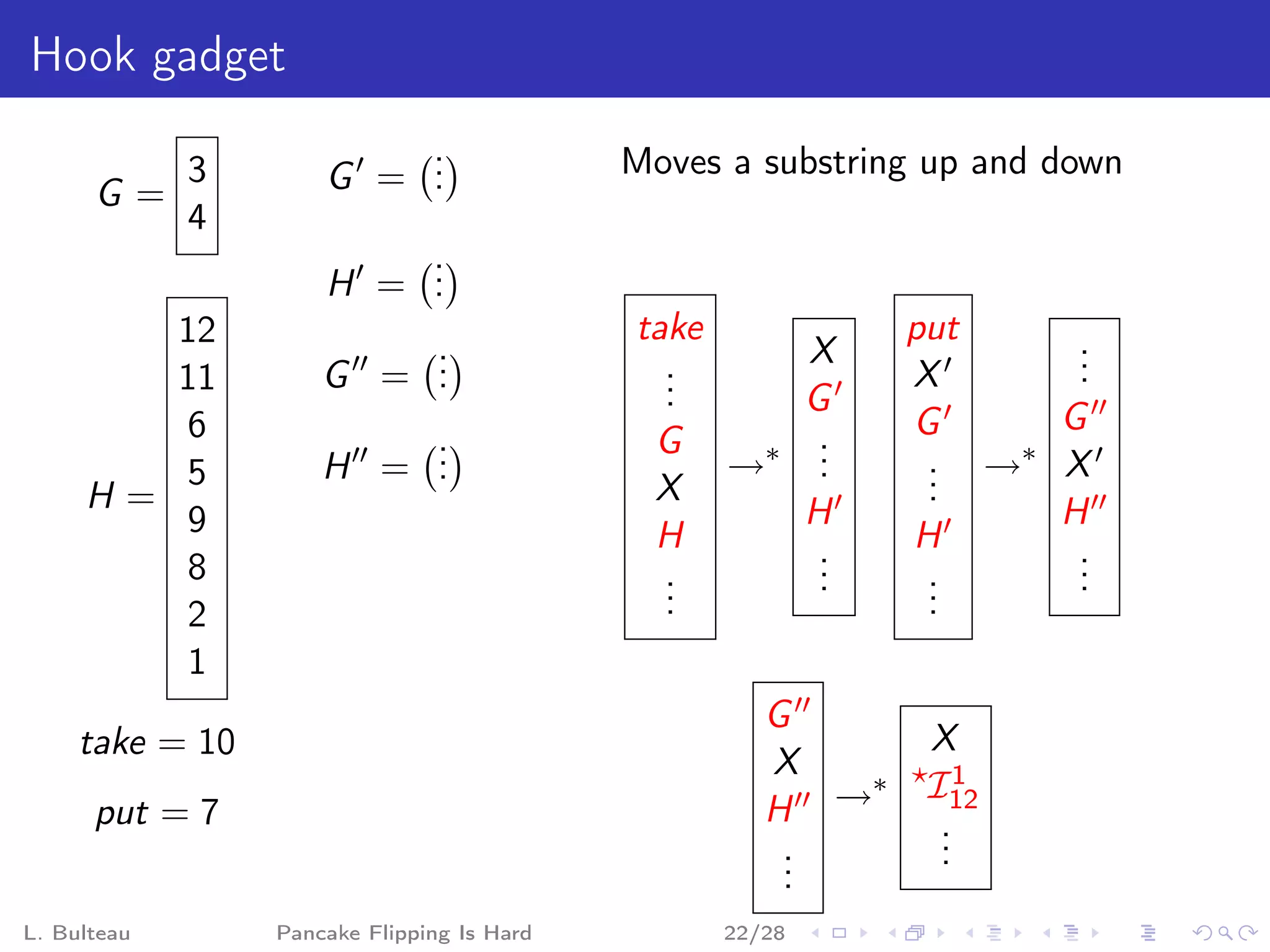
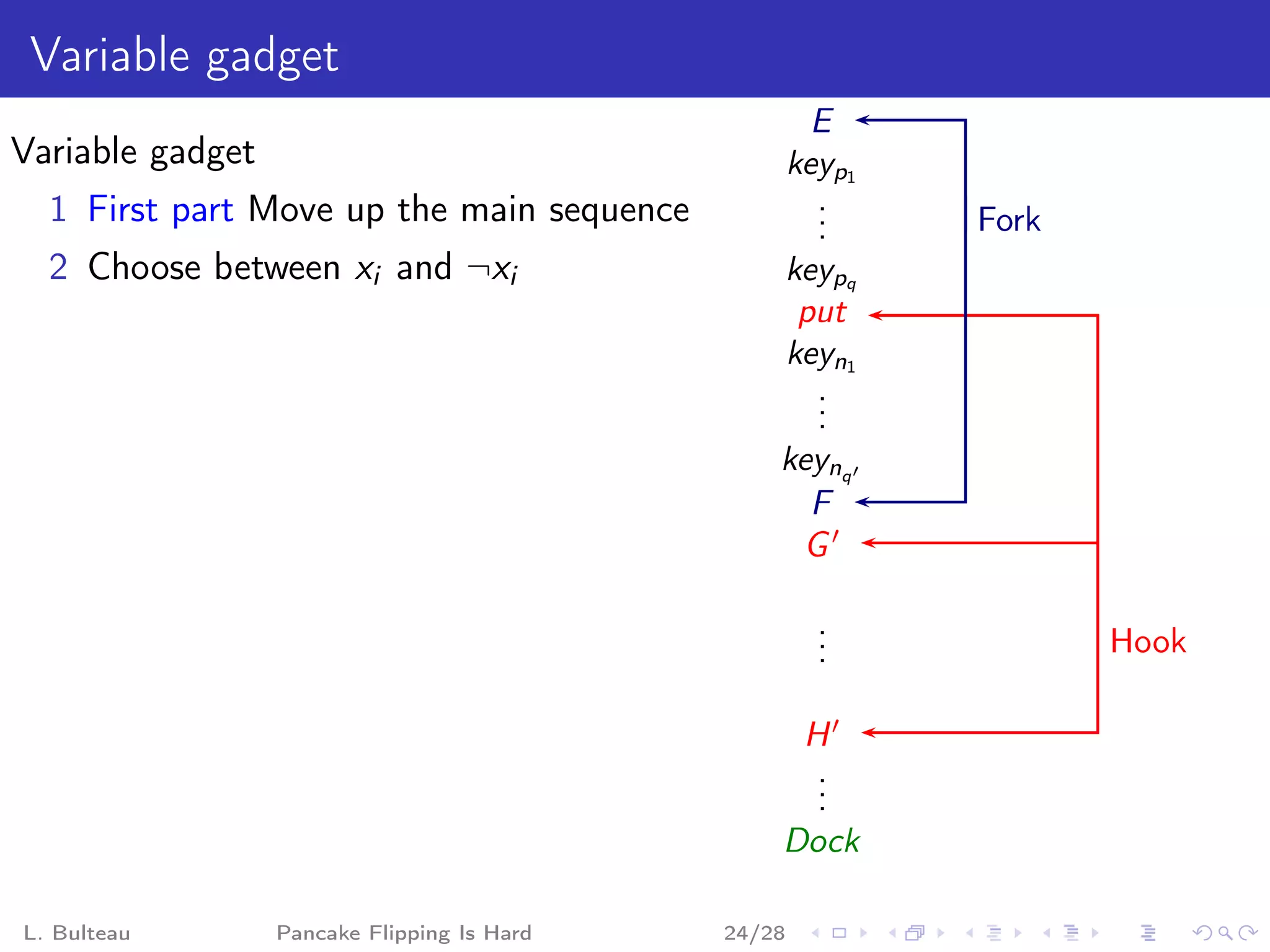
85. Clause gadget
take1
.
.
Same structure, .
with two G1
E1 Hook 1
choices: Fork 1
take2
[[a or b] or c]
put1
testc
F1
G2
Hook 2 E2
Fork 2 testa
put2
testb
F2
H2
H1
.
.
.
Dock1
L. Bulteau Pancake Flipping Is Hard Dock2
25/28

86. Overall construction
takeV1
.
. Open remaining
. Open locks in P1 Open locks in N1
locks in P1 ∪ N1
takeVl
takeC1 .
. .
. .
. .
.
. . . . .
.
.
takeCk Open remaining
Open locks in Pl Open locks in Nl
locks in Pl ∪ Nl
V1
πφ = .
.
. Test remaining
Test lock a1 Test lock b1 Test lock c1
Vl locks in {a1 , b1 , c1 }
C1
.
. .
. .
. .
. .
.
. . . . .
Ck
(docks) Test remaining
Test lock ak Test lock bk Test lock ck
locks in {ak , bk , ck }
(locks)
I
L. Bulteau Pancake Flipping Is Hard 26/28

87. Finally
There exists an efficient path from πφ to the identity iff φ is
satisfiable.
The construction requires a polynomial time.
MIN-SBPR is NP-hard.
L. Bulteau Pancake Flipping Is Hard 27/28

88. Conclusion
The complexity class of the Pancake Flipping problem is settled
There remains many intriguing questions:
What about the burnt variant?
Any approximation algorithm?
Any FPT algorithm with a relevant parameter?
Any better bound for the diameter than
1.07n ≤ f (n) ≤ 1.64n (unburnt) and
1.5n ≤ g (n) ≤ 2n (burnt)?
L. Bulteau Pancake Flipping Is Hard 28/28

89. Conclusion
The complexity class of the Pancake Flipping problem is settled
There remains many intriguing questions:
What about the burnt variant?
Any approximation algorithm?
Any FPT algorithm with a relevant parameter?
Any better bound for the diameter than
1.07n ≤ f (n) ≤ 1.64n (unburnt) and
1.5n ≤ g (n) ≤ 2n (burnt)?
Thank you!
L. Bulteau Pancake Flipping Is Hard 28/28