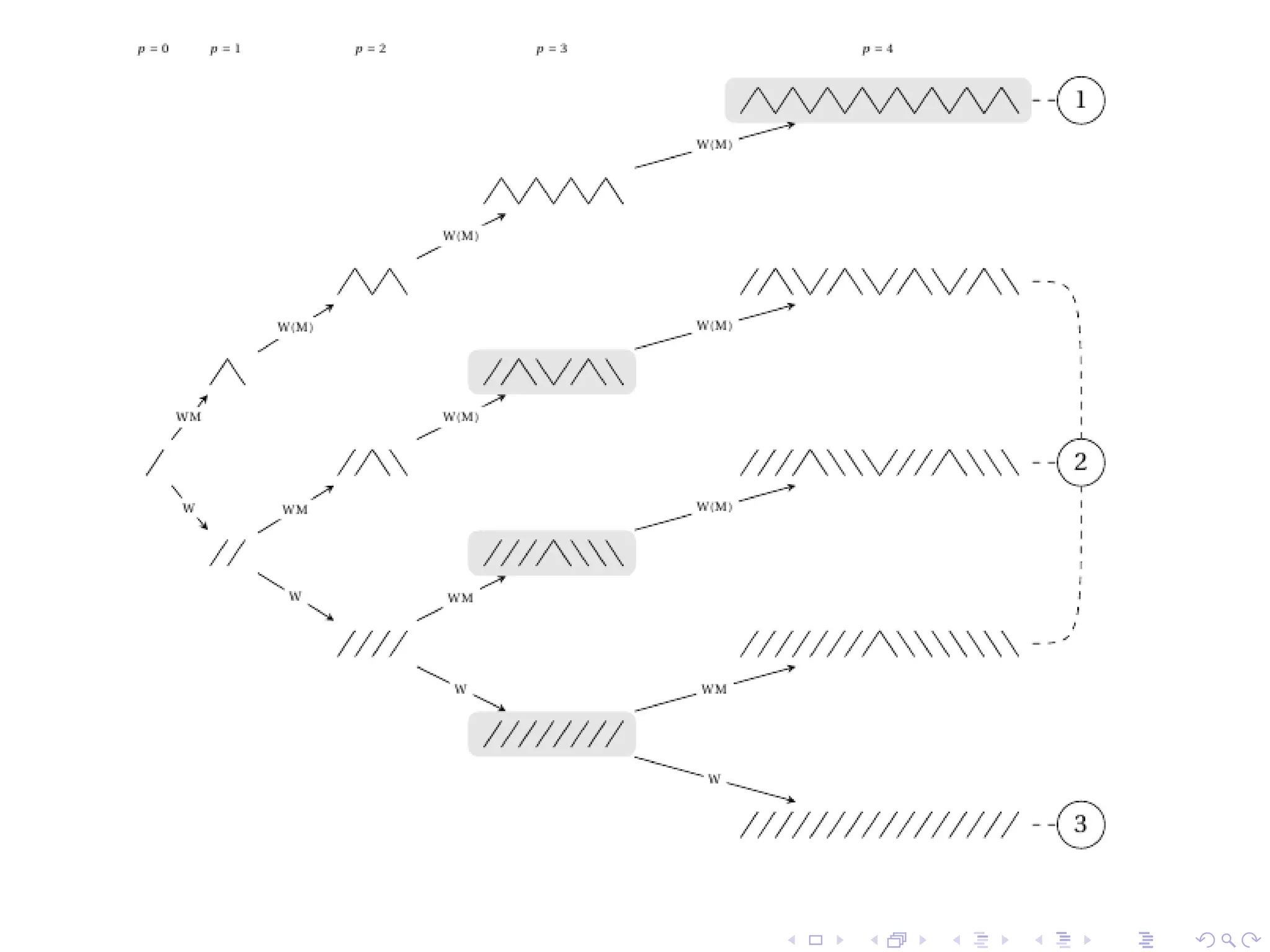
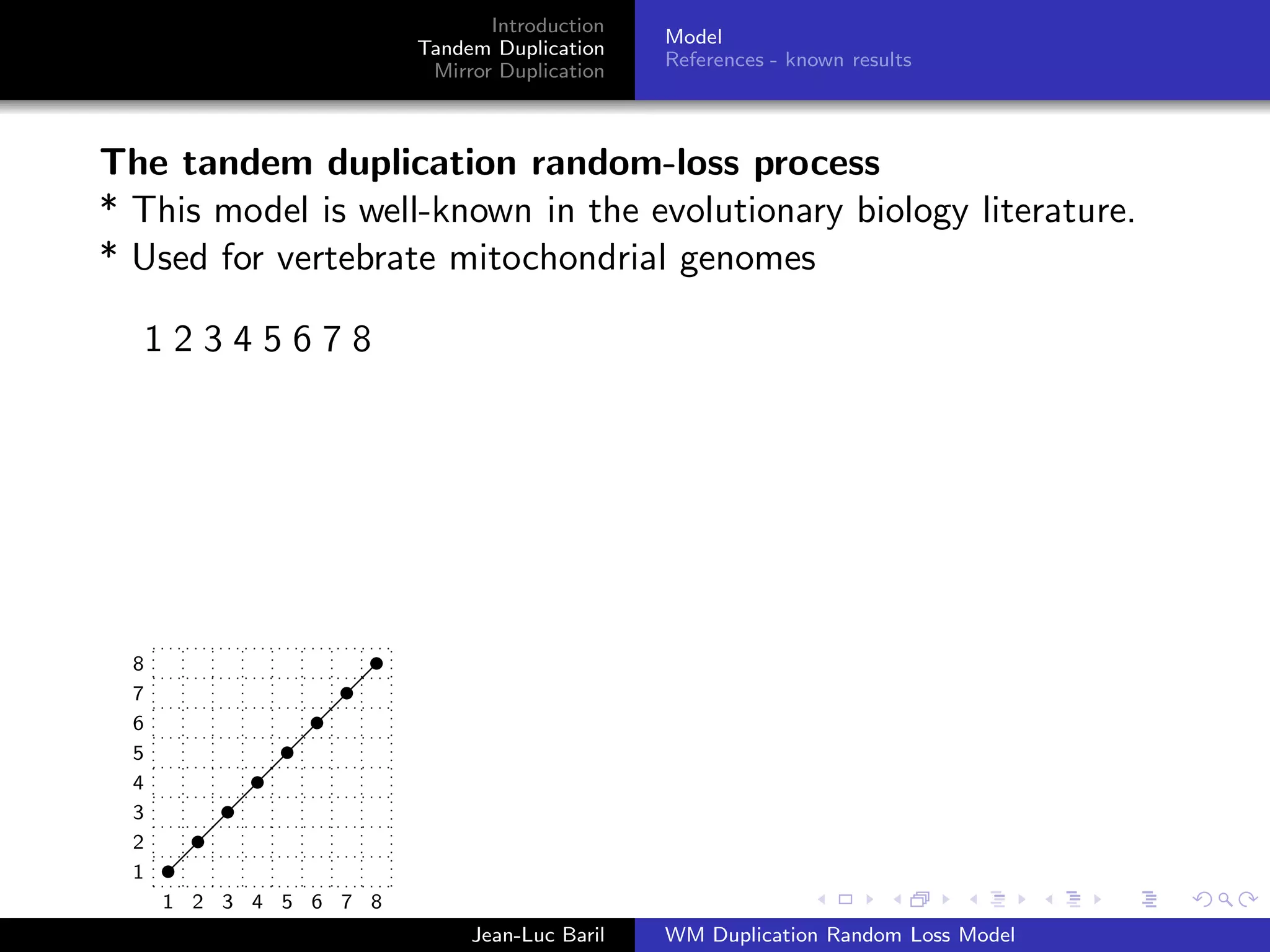
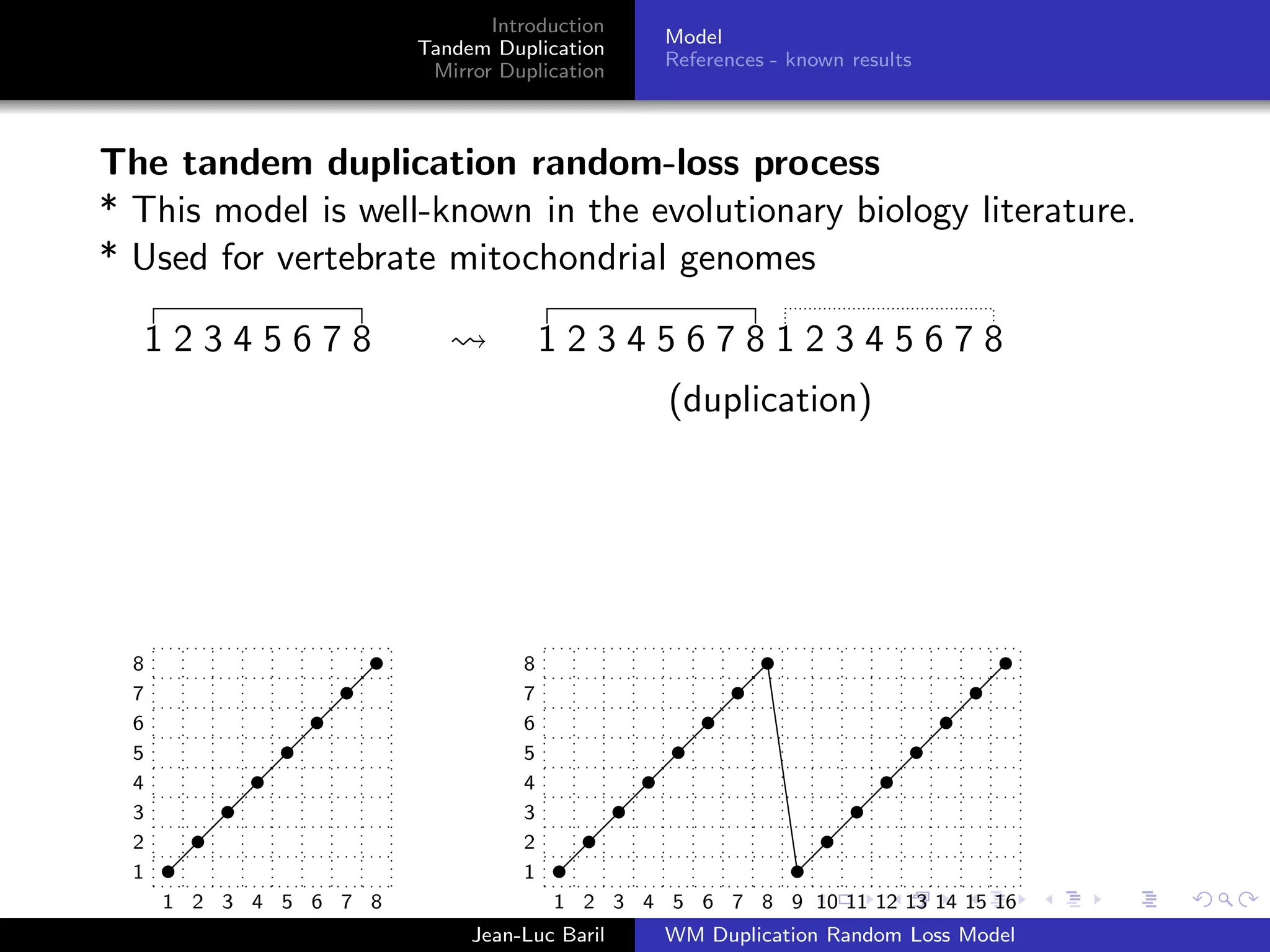
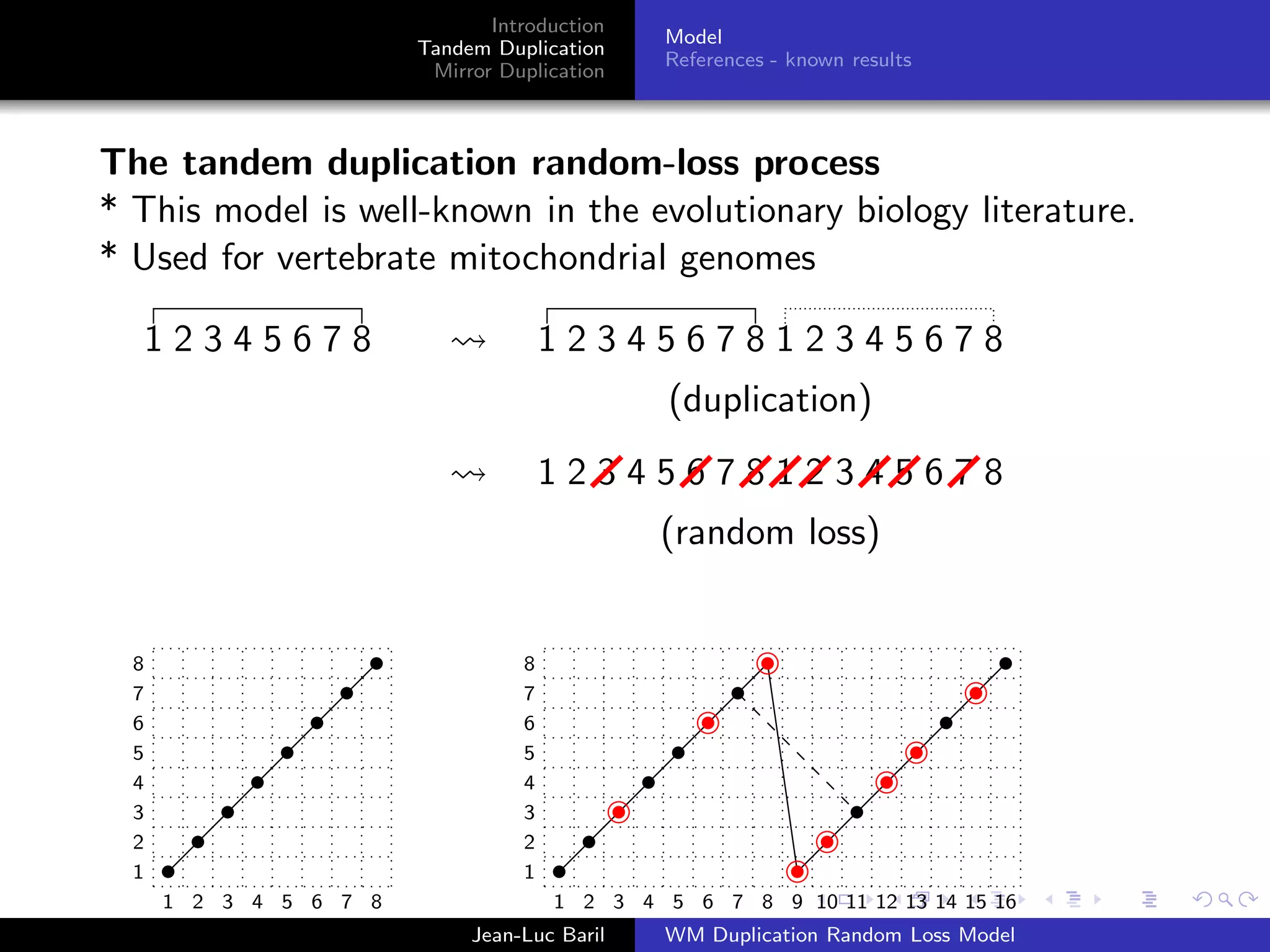
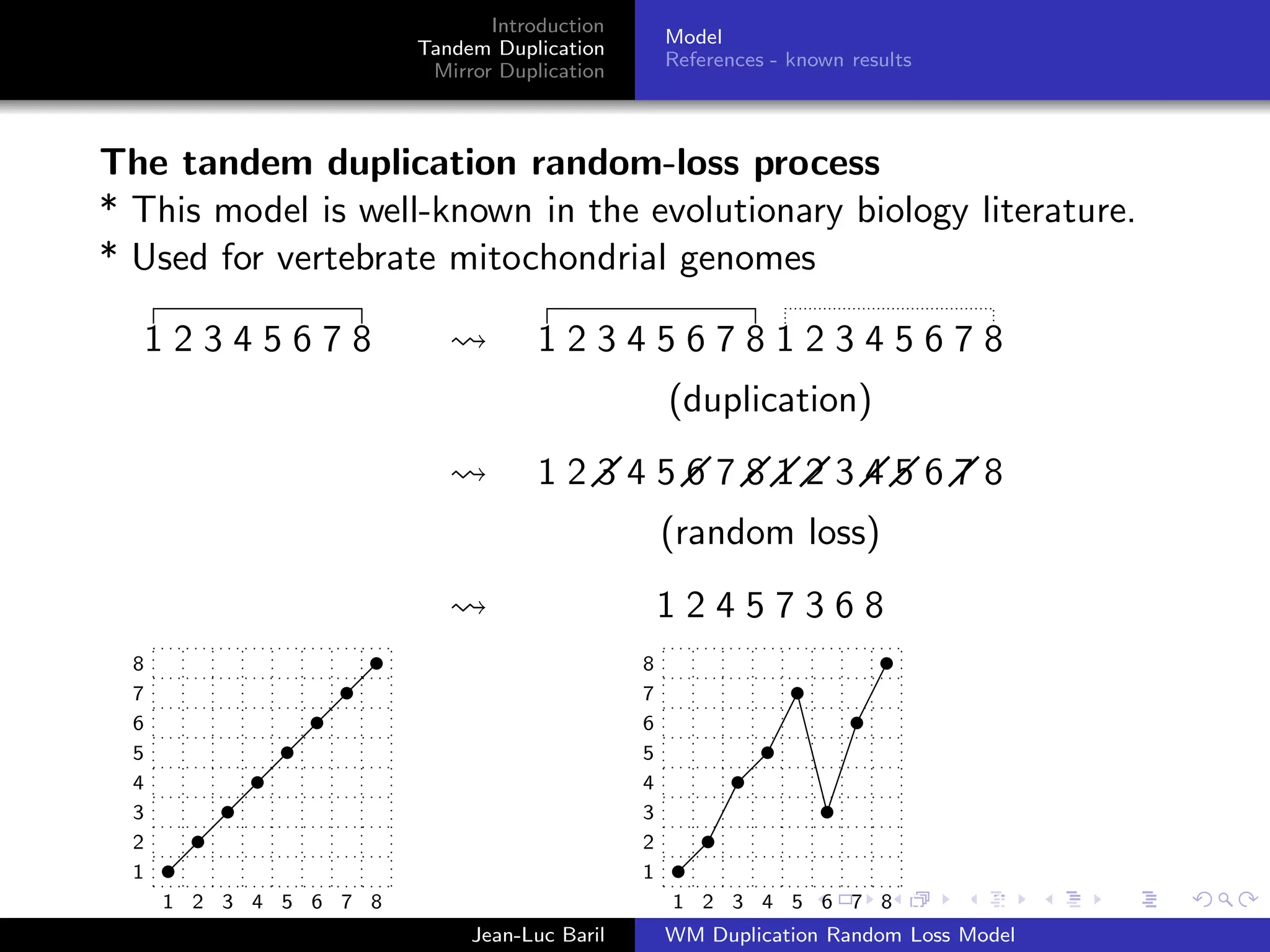
The document discusses the tandem duplication and mirror duplication processes in the context of a random loss model concerning genomic permutations. It introduces definitions and properties of permutations and presents the mathematical frameworks needed to understand how these duplications affect genomic sequences. Additionally, it references previous studies and established models in evolutionary biology related to these concepts.

1. Introduction
Tandem Duplication
Mirror Duplication
Whole Mirror Duplication Random Loss Model and
Pattern Avoiding Permutations
Jean-Luc Baril and R´mi Vernay
e
barjl@u-bourgogne.fr
http://jl.baril.u-bourgogne.fr
Laboratory LE2I – University of Burgundy – Dijon
Jean-Luc Baril WM Duplication Random Loss Model

2. Introduction
The Genome - Definition
Tandem Duplication
Pattern in permutations
Mirror Duplication
Some definitions and notations
genome = set of chromosomes
chromosome = sequence of genes
gene = sequence of Ad´nine, Guanine, Cytosine, Thynmine
e
(AGCT)
genome → n-length permutation σ = σ1 σ2 σ3 . . . σn
Sn = the set of n-length permutations
Graphical representation of the permutation
σ=84 6 2 5 71 3
8
7
6
5
4
3
2
1
1 2 3 4 5 6 7 8
8 4 6 2 5 WM1 3
Jean-Luc Baril
7 Duplication Random Loss Model

3. Introduction
The Genome - Definition
Tandem Duplication
Pattern in permutations
Mirror Duplication
Let σ = σ1 σ2 . . . σn be a permutation:
ascent → σi < σi +1
run up → σi < σi +1 < · · · < σj
descent, run-down
valley → σi −1 > σi < σi +1
Alternating permutation → σ1 > σ2 < σ3 > σ4 < σ5 > · · ·
8
7
6
5
4
3
2
1
1 2 3 4 5 6 7 8
Jean-Luc Baril WM Duplication Random Loss Model

4. Introduction
The Genome - Definition
Tandem Duplication
Pattern in permutations
Mirror Duplication
Let σ = σ1 σ2 . . . σn be a permutation:
ascent → σi < σi +1
run up → σi < σi +1 < · · · < σj
descent, run-down
valley → σi −1 > σi < σi +1
Alternating permutation → σ1 > σ2 < σ3 > σ4 < σ5 > · · ·
8
7
6
5
4
3
2
1
1 2 3 4 5 6 7 8
Jean-Luc Baril WM Duplication Random Loss Model

5. Introduction
The Genome - Definition
Tandem Duplication
Pattern in permutations
Mirror Duplication
Let σ = σ1 σ2 . . . σn be a permutation:
ascent → σi < σi +1
run up → σi < σi +1 < · · · < σj
descent, run-down
valley → σi −1 > σi < σi +1
Alternating permutation → σ1 > σ2 < σ3 > σ4 < σ5 > · · ·
8
7
6
5
4
3
2
1
1 2 3 4 5 6 7 8
Jean-Luc Baril WM Duplication Random Loss Model

6. Introduction
The Genome - Definition
Tandem Duplication
Pattern in permutations
Mirror Duplication
Let σ = σ1 σ2 . . . σn be a permutation:
ascent → σi < σi +1
run up → σi < σi +1 < · · · < σj
descent, run-down
valley → σi −1 > σi < σi +1
Alternating permutation → σ1 > σ2 < σ3 > σ4 < σ5 > · · ·
8
7
6
5
4
3
2
1
1 2 3 4 5 6 7 8
Jean-Luc Baril WM Duplication Random Loss Model

7. Introduction
The Genome - Definition
Tandem Duplication
Pattern in permutations
Mirror Duplication
Let σ = σ1 σ2 . . . σn be a permutation:
ascent → σi < σi +1
run up → σi < σi +1 < · · · < σj
descent, run-down
valley → σi −1 > σi < σi +1
Alternating permutation → σ1 > σ2 < σ3 > σ4 < σ5 > · · ·
8
7
6
5
4
3
2
1
1 2 3 4 5 6 7 8
Jean-Luc Baril WM Duplication Random Loss Model

8. Introduction
The Genome - Definition
Tandem Duplication
Pattern in permutations
Mirror Duplication
Definition:
σ ∈ Sn contains the pattern π ∈ Sk (π σ) if:
∃1 ≤ i1 < i2 < · · · < ik ≤ n such that σi1 σi2 . . . σik is
order-isomorphic to π, i.e.,
∀1 ≤ u, v ≤ k, σi u < σi v ⇔ π u < π v .
Example: σ = 8 4 6 2 5 7 1 3 contains the pattern π = 4132
8
7
6
5
4
3
2
1
1 2 3 4 5 6 7 8
84625713
Jean-Luc Baril WM Duplication Random Loss Model

9. Introduction
The Genome - Definition
Tandem Duplication
Pattern in permutations
Mirror Duplication
Class of permutations
C is a class of permutations if C is stable for the relation
σ ∈ C and π σ ⇒ π ∈ C.
Basis for a class of permutations
A class C of permutations is characterized by its basis B:
B = {σ ∈ C, ∀π ≺ σ with π = σ, π ∈ C}
/
We have C = S(B) where S(B) is the class of permutations
avoiding all patterns in B.
Jean-Luc Baril WM Duplication Random Loss Model

10. Introduction
Model
Tandem Duplication
References - known results
Mirror Duplication
The tandem duplication random-loss process
* This model is well-known in the evolutionary biology literature.
* Used for vertebrate mitochondrial genomes
12345678 1234567812345678
1234567812345678
12457368
8
7
6
5
4
3
2
1
1 2 3 4 5 6 7 8
Jean-Luc Baril WM Duplication Random Loss Model

11. Introduction
Model
Tandem Duplication
References - known results
Mirror Duplication
The tandem duplication random-loss process
* This model is well-known in the evolutionary biology literature.
* Used for vertebrate mitochondrial genomes
12345678 1234567812345678
(duplication)
1234567812345678
12457368
8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Jean-Luc Baril WM Duplication Random Loss Model

12. Introduction
Model
Tandem Duplication
References - known results
Mirror Duplication
The tandem duplication random-loss process
* This model is well-known in the evolutionary biology literature.
* Used for vertebrate mitochondrial genomes
12345678 1234567812345678
(duplication)
1234567812345678
(random loss)
12457368
8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Jean-Luc Baril WM Duplication Random Loss Model

13. Introduction
Model
Tandem Duplication
References - known results
Mirror Duplication
The tandem duplication random-loss process
* This model is well-known in the evolutionary biology literature.
* Used for vertebrate mitochondrial genomes
12345678 1234567812345678
(duplication)
1234567812345678
(random loss)
12457368
8 8 8
7 7 7
6 6 6
5 5 5
4 4 4
3 3 3
2 2 2
1 1 1
1 2 3 4 5 6 7 8 1 2 3 4 1 2 3 4 5 6 7 8 5 14 15 16
Jean-Luc Baril WM Duplication Random Loss Model

14. Introduction
Model
Tandem Duplication
References - known results
Mirror Duplication
2006 K. Chaudhuri, K. Chen, R. Mihaescu and S. Rao
On the tandem duplication-random loss model
of genome rearrangement,SODA
Tandem duplication random-loss process of an
interval of size K ;
Efficient algorithm for the distance between 2
genomes
Jean-Luc Baril WM Duplication Random Loss Model

15. Introduction
Model
Tandem Duplication
References - known results
Mirror Duplication
2006 K. Chaudhuri, K. Chen, R. Mihaescu and S. Rao
On the tandem duplication-random loss model of genome rearrangement,SODA
2009 M. Bouvel and D. Rossin
A variant of the tandem duplication-random loss
model of genome rearrangement, TCS
Permutations obtained after p duplications of an
interval of size K define a class of permutations
avoiding some patterns in B.
B = set of minimal permutations with d = 2p
descents.
Jean-Luc Baril WM Duplication Random Loss Model

16. Introduction
Model
Tandem Duplication
References - known results
Mirror Duplication
2006 K. Chaudhuri, K. Chen, R. Mihaescu and S. Rao
On the tandem duplication-random loss model of genome rearrangement,SODA
2009 M. Bouvel and D. Rossin
A variant of the tandem duplication-random loss model of genome rearrangement, TCS
2010 M. Bouvel and E. Pergola
Posets and permutations in the duplication-loss
model: minimal permutations with d descents,
Theoretical Computer Science
enumeration minimal permutations of size
n = d + 1, d + 2, 2d;
Jean-Luc Baril WM Duplication Random Loss Model

17. Introduction
Model
Tandem Duplication
References - known results
Mirror Duplication
2006 K. Chaudhuri, K. Chen, R. Mihaescu and S. Rao
On the tandem duplication-random loss model of genome rearrangement,SODA
2009 M. Bouvel and D. Rossin
A variant of the tandem duplication-random loss model of genome rearrangement, TCS
2010 M. Bouvel and E. Pergola
Posets and permutations in the duplication-loss model: minimal permutations with d
descents, Theoretical Computer Science
2010 T. Mansour and S. H.F. Yan
Minimal permutations with d descents, European
Journal of Combinatorics
enumeration minimal permutations of size
n = 2d − 1
Jean-Luc Baril WM Duplication Random Loss Model

18. Introduction
Model
Tandem Duplication
References - known results
Mirror Duplication
2006 K. Chaudhuri, K. Chen, R. Mihaescu and S. Rao
On the tandem duplication-random loss model of genome rearrangement,SODA
2009 M. Bouvel and D. Rossin
A variant of the tandem duplication-random loss model of genome rearrangement, TCS
2010 M. Bouvel and E. Pergola
Posets and permutations in the duplication-loss model: minimal permutations with d
descents, Theoretical Computer Science
2010 T. Mansour and S. H.F. Yan
Minimal permutations with d descents, European Journal of Combinatorics
2010 M. Bouvel and L. Ferrari
On the enumeration of d-minimal permutations,
Arxiv
prove that the number of minimal permutations with
d descents can be obtained by computing some
determinants, but they cannot provide a general
closed formula
Jean-Luc Baril WM Duplication Random Loss Model

19. Model
Introduction
Theorems
Tandem Duplication
Algo σ → 12 · · · n
Mirror Duplication
Algo 12 · · · n → σ
The whole mirror duplication random-loss process
12345678 1234567887654321
1234567887654321
14578632
8
7
6
5
4
3
2
1
1 2 3 4 5 6 7 8
Jean-Luc Baril WM Duplication Random Loss Model

20. Model
Introduction
Theorems
Tandem Duplication
Algo σ → 12 · · · n
Mirror Duplication
Algo 12 · · · n → σ
The whole mirror duplication random-loss process
12345678 1234567887654321
(mirror duplication)
1234567887654321
14578632
8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Jean-Luc Baril WM Duplication Random Loss Model

21. Model
Introduction
Theorems
Tandem Duplication
Algo σ → 12 · · · n
Mirror Duplication
Algo 12 · · · n → σ
The whole mirror duplication random-loss process
12345678 1234567887654321
(mirror duplication)
1234567887654321
(random loss)
14578632
8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Jean-Luc Baril WM Duplication Random Loss Model

22. Model
Introduction
Theorems
Tandem Duplication
Algo σ → 12 · · · n
Mirror Duplication
Algo 12 · · · n → σ
The whole mirror duplication random-loss process
12345678 1234567887654321
(mirror duplication)
1234567887654321
(random loss)
14578632
8 8 8
7 7 7
6 6 6
5 5 5
4 4 4
3 3 3
2 2 2
1 1 1
1 2 3 4 5 6 7 8 1 2 3 4 1 2 3 4 5 6 7 8 13 14 15 16
Jean-Luc Baril WM Duplication Random Loss Model

23. Model
Introduction
Theorems
Tandem Duplication
Algo σ → 12 · · · n
Mirror Duplication
Algo 12 · · · n → σ
Theorem 1
The class C(p) of permutations obtained from the identity after a
given number p of whole mirror duplications is the class of
permutations with at most 2p−1 − 1 valleys.
2p−2 − 1 valleys
Jean-Luc Baril WM Duplication Random Loss Model

24. Model
Introduction
Theorems
Tandem Duplication
Algo σ → 12 · · · n
Mirror Duplication
Algo 12 · · · n → σ
Theorem 1
The class C(p) of permutations obtained from the identity after a
given number p of whole mirror duplications is the class of
permutations with at most 2p−1 − 1 valleys.
2p−1 − 1 = 2p−2 − 1 + 2p−2 − 1 + 1 valleys
Jean-Luc Baril WM Duplication Random Loss Model

25. Model
Introduction
Theorems
Tandem Duplication
Algo σ → 12 · · · n
Mirror Duplication
Algo 12 · · · n → σ
2p−2 − 1 < k valleys ≤ 2p−1 − 1
Jean-Luc Baril WM Duplication Random Loss Model

26. Model
Introduction
Theorems
Tandem Duplication
Algo σ → 12 · · · n
Mirror Duplication
Algo 12 · · · n → σ
2p−2 − 1 valleys
Jean-Luc Baril WM Duplication Random Loss Model

27. Model
Introduction
Theorems
Tandem Duplication
Algo σ → 12 · · · n
Mirror Duplication
Algo 12 · · · n → σ
Jean-Luc Baril WM Duplication Random Loss Model

28. Model
Introduction
Theorems
Tandem Duplication
Algo σ → 12 · · · n
Mirror Duplication
Algo 12 · · · n → σ
Jean-Luc Baril WM Duplication Random Loss Model

29. Model
Introduction
Theorems
Tandem Duplication
Algo σ → 12 · · · n
Mirror Duplication
Algo 12 · · · n → σ
Jean-Luc Baril WM Duplication Random Loss Model

30. Model
Introduction
Theorems
Tandem Duplication
Algo σ → 12 · · · n
Mirror Duplication
Algo 12 · · · n → σ
Theorem 2
The class C(p) of permutations obtained after a given number p of
whole mirror duplications is the class of permutations avoiding the
alternating permutations of length 2p + 1.
For p = 1, C(1) = S(213, 312)
For p = 2, C(2) =
S(21435, 31425, 41325, 32415, 42315, 21534, 31524, 51324, 32514,
52314, 41523, 51423, 42513, 52413, 43512, 53412)
|C(p)| given by the generating function:
1 1 1 1
1− + y − 1 · tan x y − 1 + arctan √
1−y y y y −1
Jean-Luc Baril WM Duplication Random Loss Model

31. Model
Introduction
Theorems
Tandem Duplication
Algo σ → 12 · · · n
Mirror Duplication
Algo 12 · · · n → σ
Algorithm 1 for a shortest path from 12 · · · n to σ ∈ Sn .
8
7
6
5
4
3
2
1
1 2 3 4 5 6 7 8
13625748
Complexity: O(n · log val(σ)) < O(n · log n)
Jean-Luc Baril WM Duplication Random Loss Model

32. Model
Introduction
Theorems
Tandem Duplication
Algo σ → 12 · · · n
Mirror Duplication
Algo 12 · · · n → σ
Algorithm 1 for a shortest path from 12 · · · n to σ ∈ Sn .
8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8
13625748 134678
Complexity: O(n · log val(σ)) < O(n · log n)
Jean-Luc Baril WM Duplication Random Loss Model

33. Model
Introduction
Theorems
Tandem Duplication
Algo σ → 12 · · · n
Mirror Duplication
Algo 12 · · · n → σ
Algorithm 1 for a shortest path from 12 · · · n to σ ∈ Sn .
8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8
13625748 13467852
Complexity: O(n · log val(σ)) < O(n · log n)
Jean-Luc Baril WM Duplication Random Loss Model

34. Model
Introduction
Theorems
Tandem Duplication
Algo σ → 12 · · · n
Mirror Duplication
Algo 12 · · · n → σ
Algorithm 1 for a shortest path from 12 · · · n to σ ∈ Sn .
8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8
13625748
⇒ O(n) 13684257
8
7
6
5
4
3
2
1
1 2 3 4 5 6 7 8
12345678
Complexity: O(n · log val(σ)) < O(n · log n)
Jean-Luc Baril WM Duplication Random Loss Model

35. Model
Introduction
Theorems
Tandem Duplication
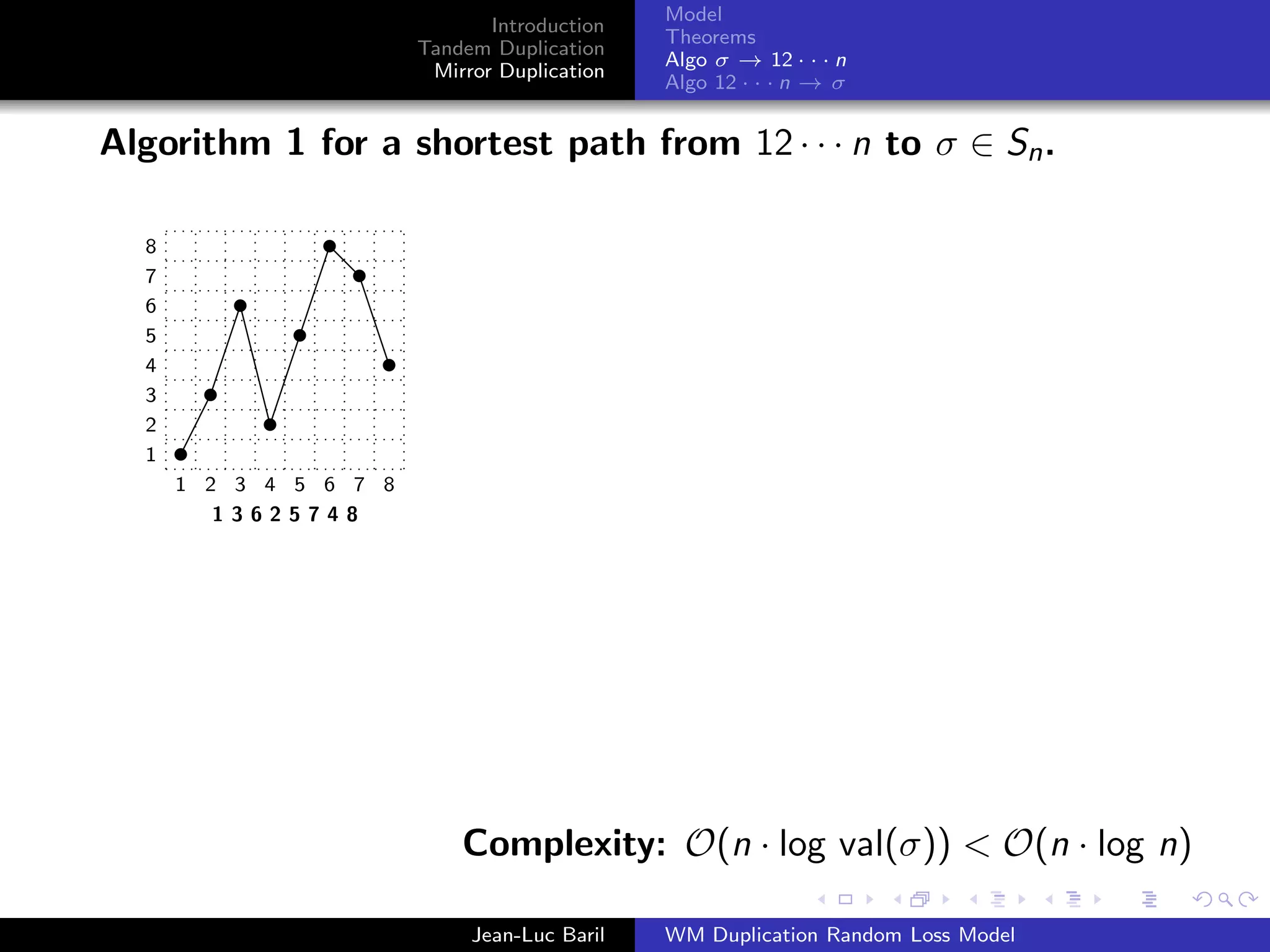
Algo σ → 12 · · · n
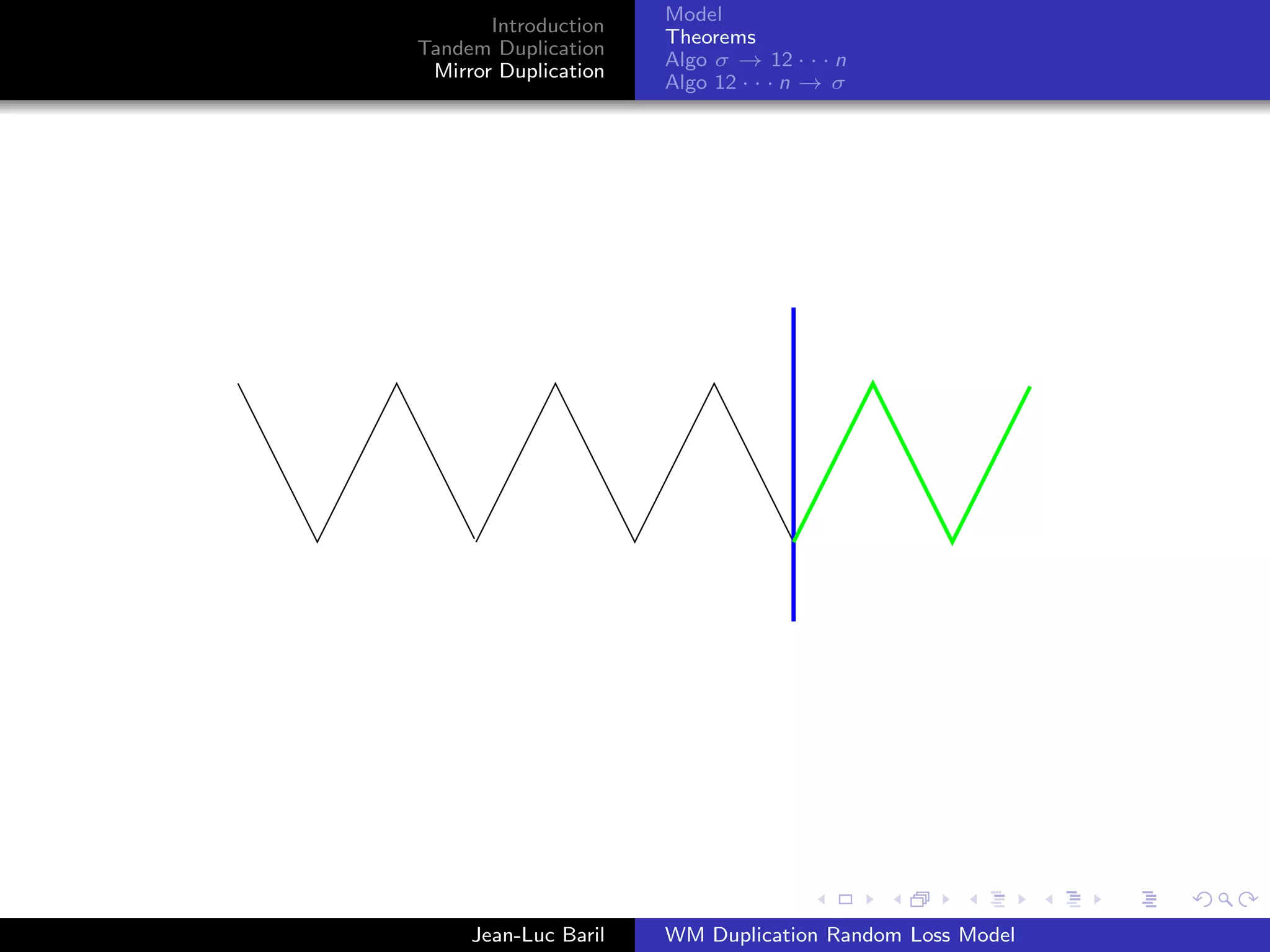
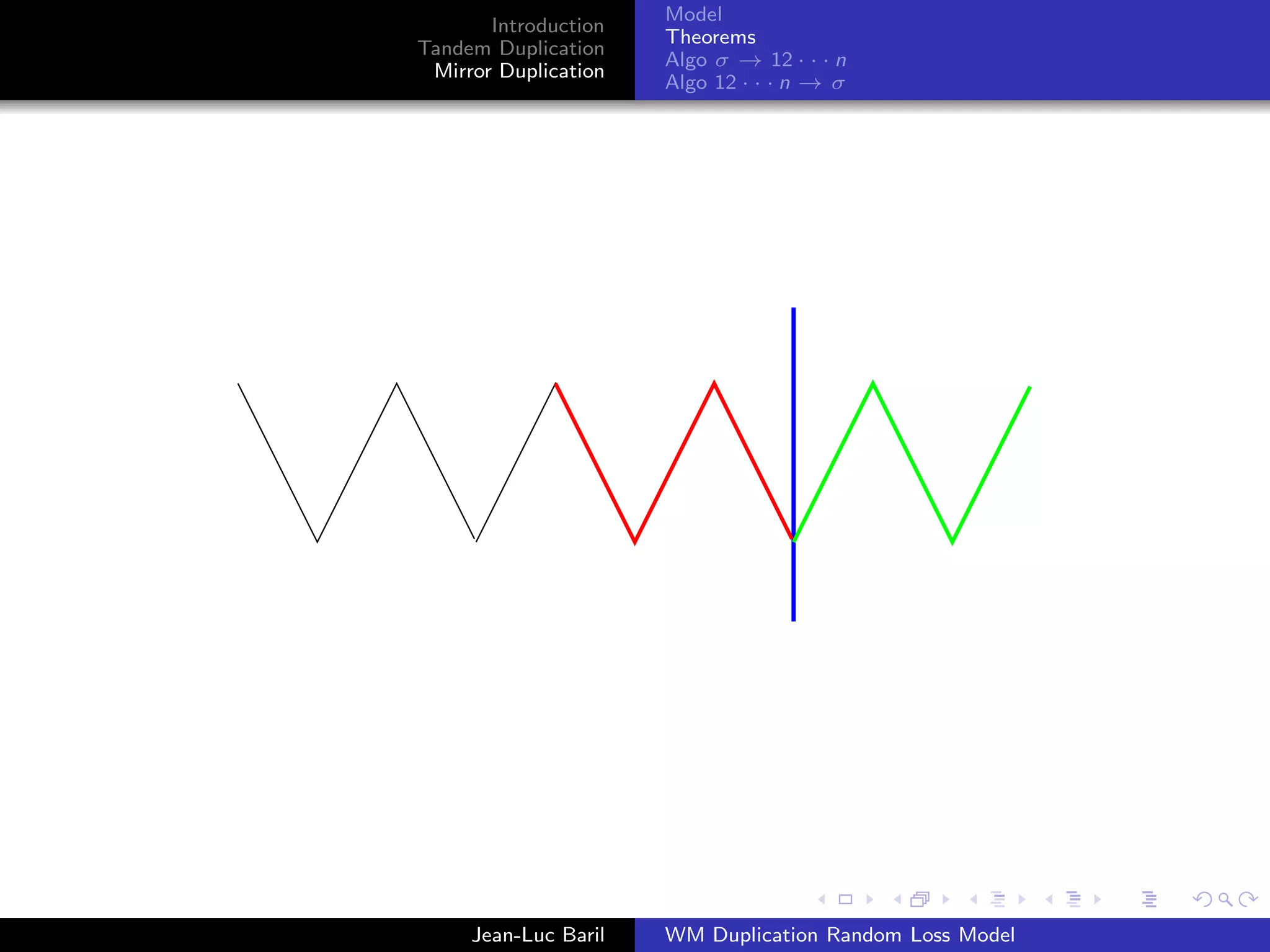
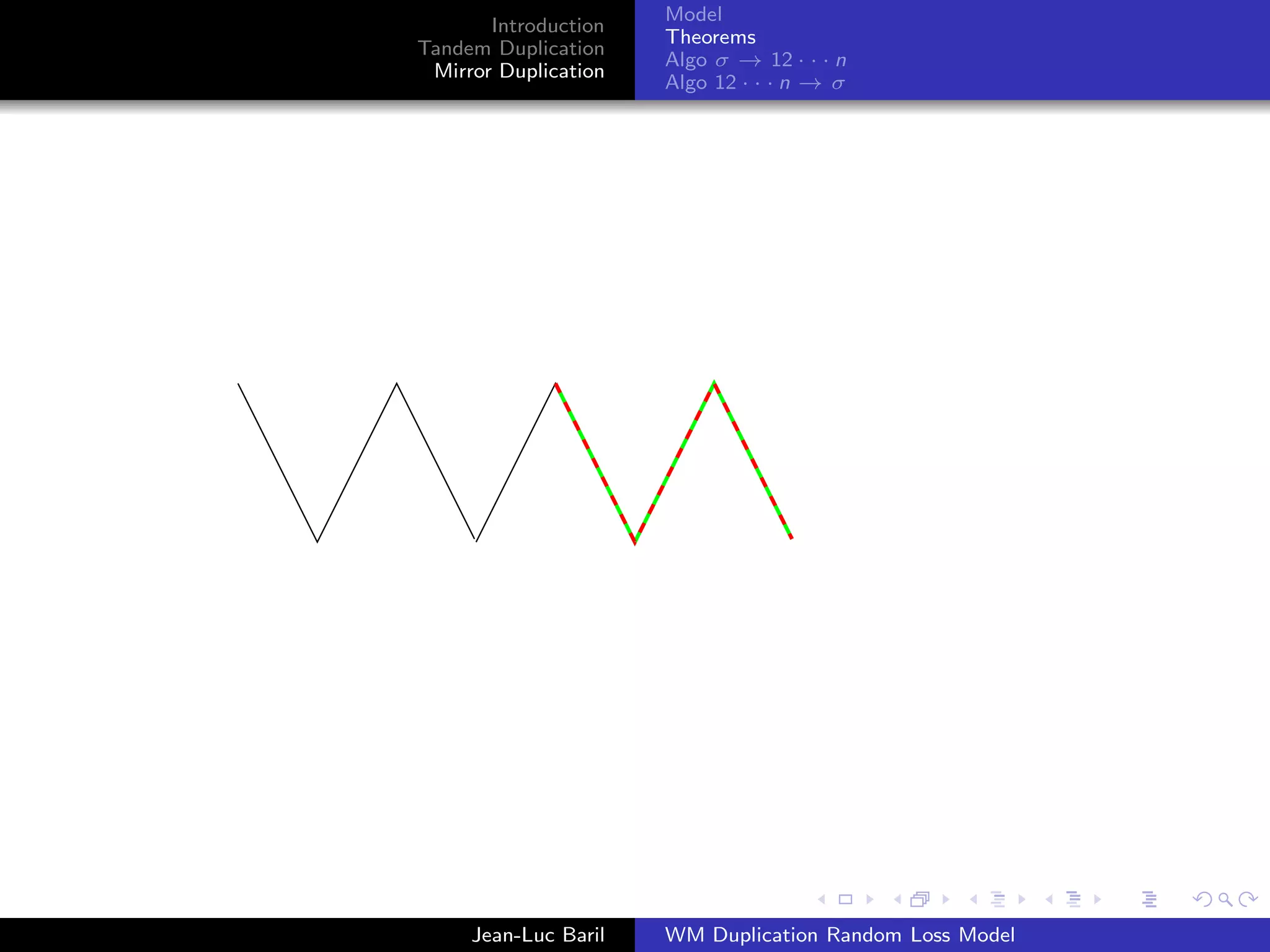
Mirror Duplication
Algo 12 · · · n → σ
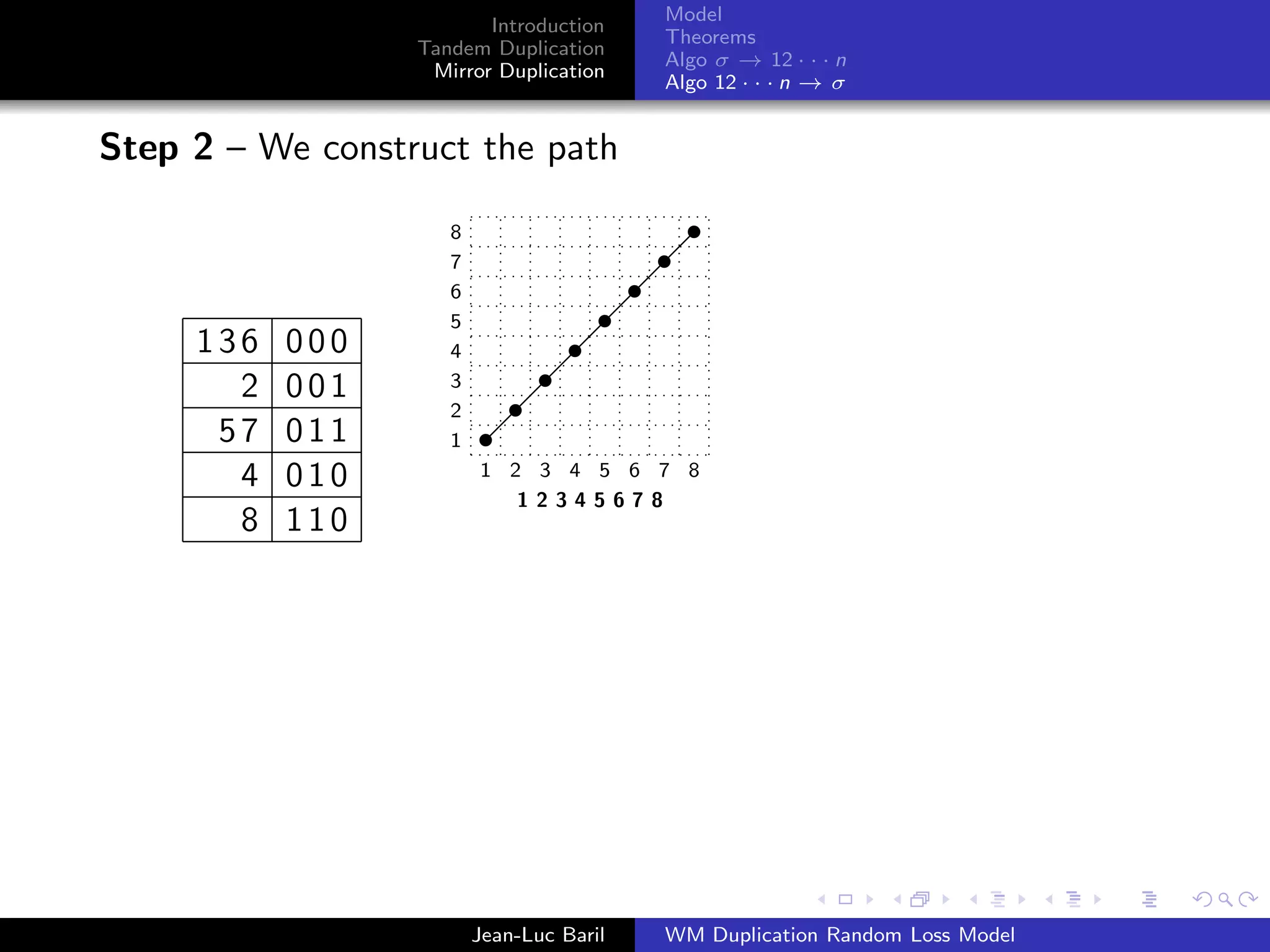
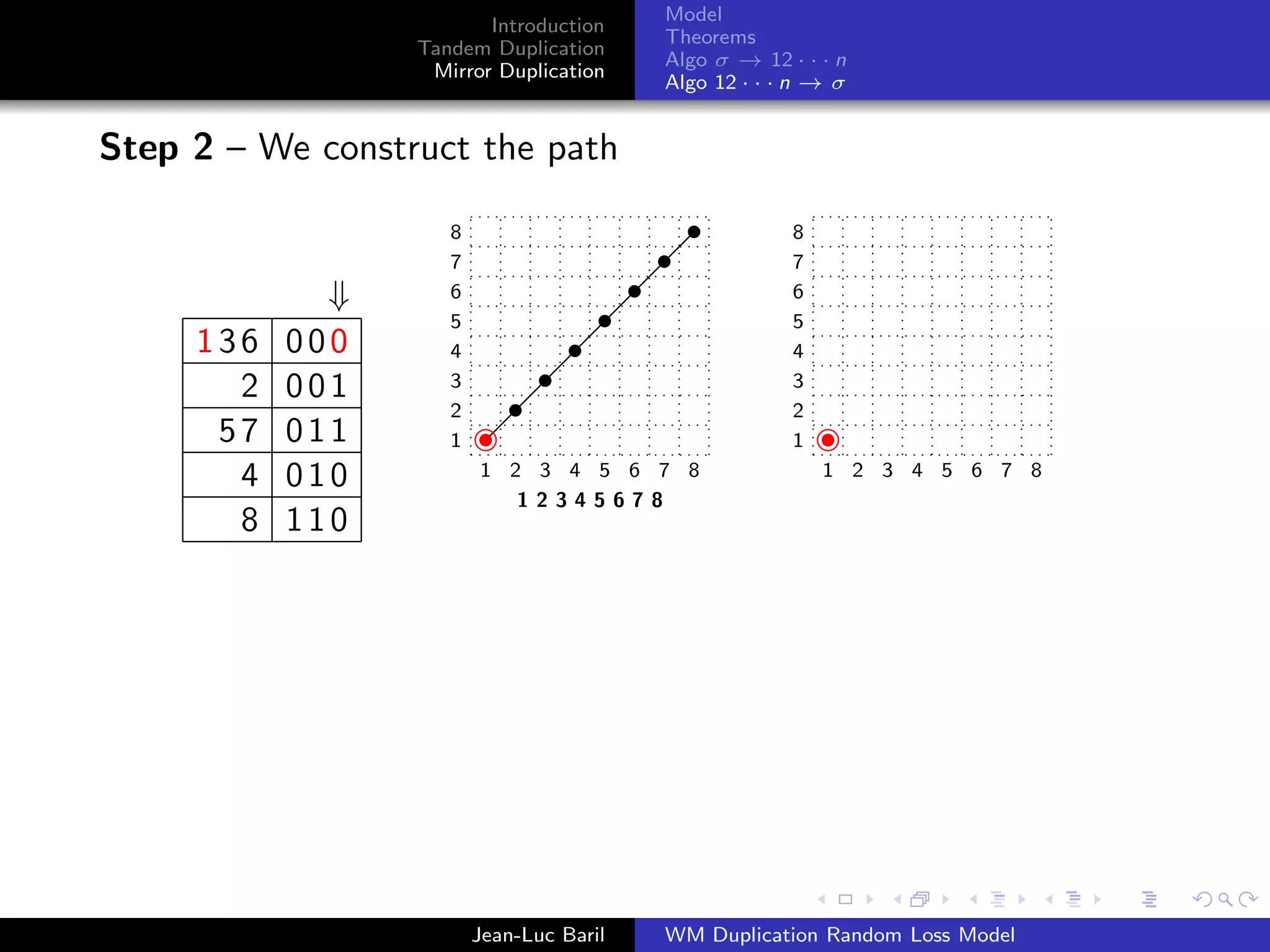
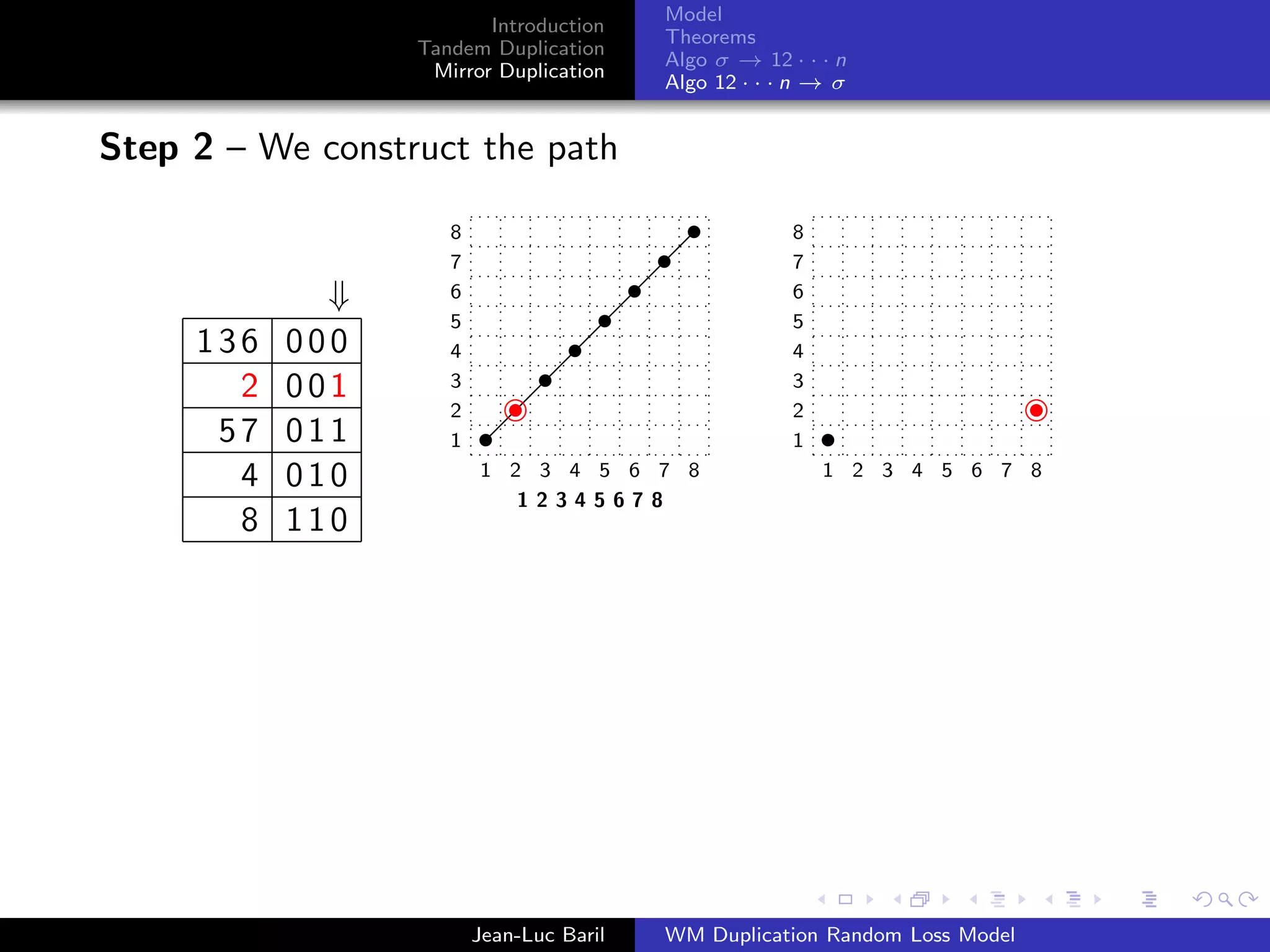
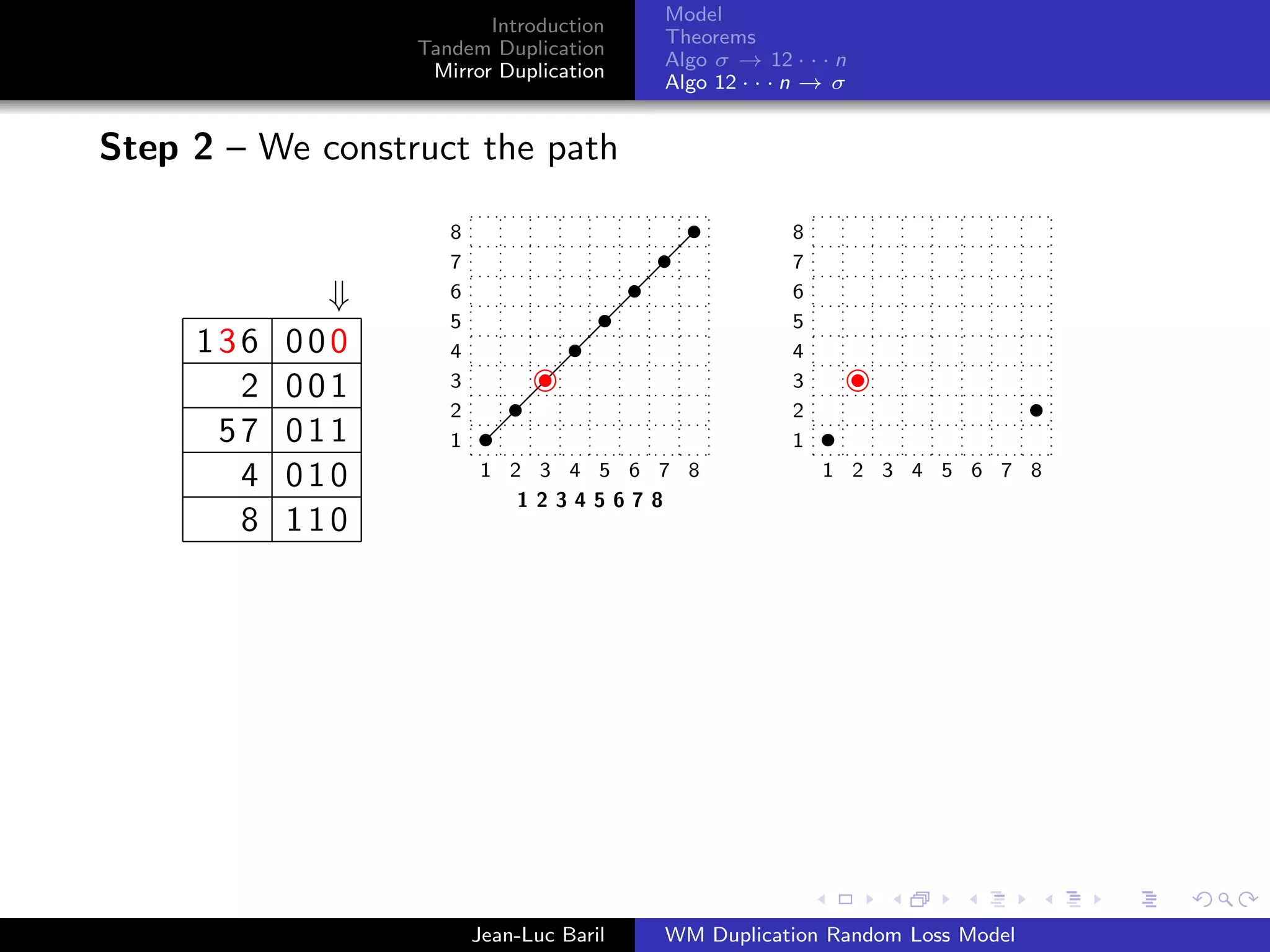
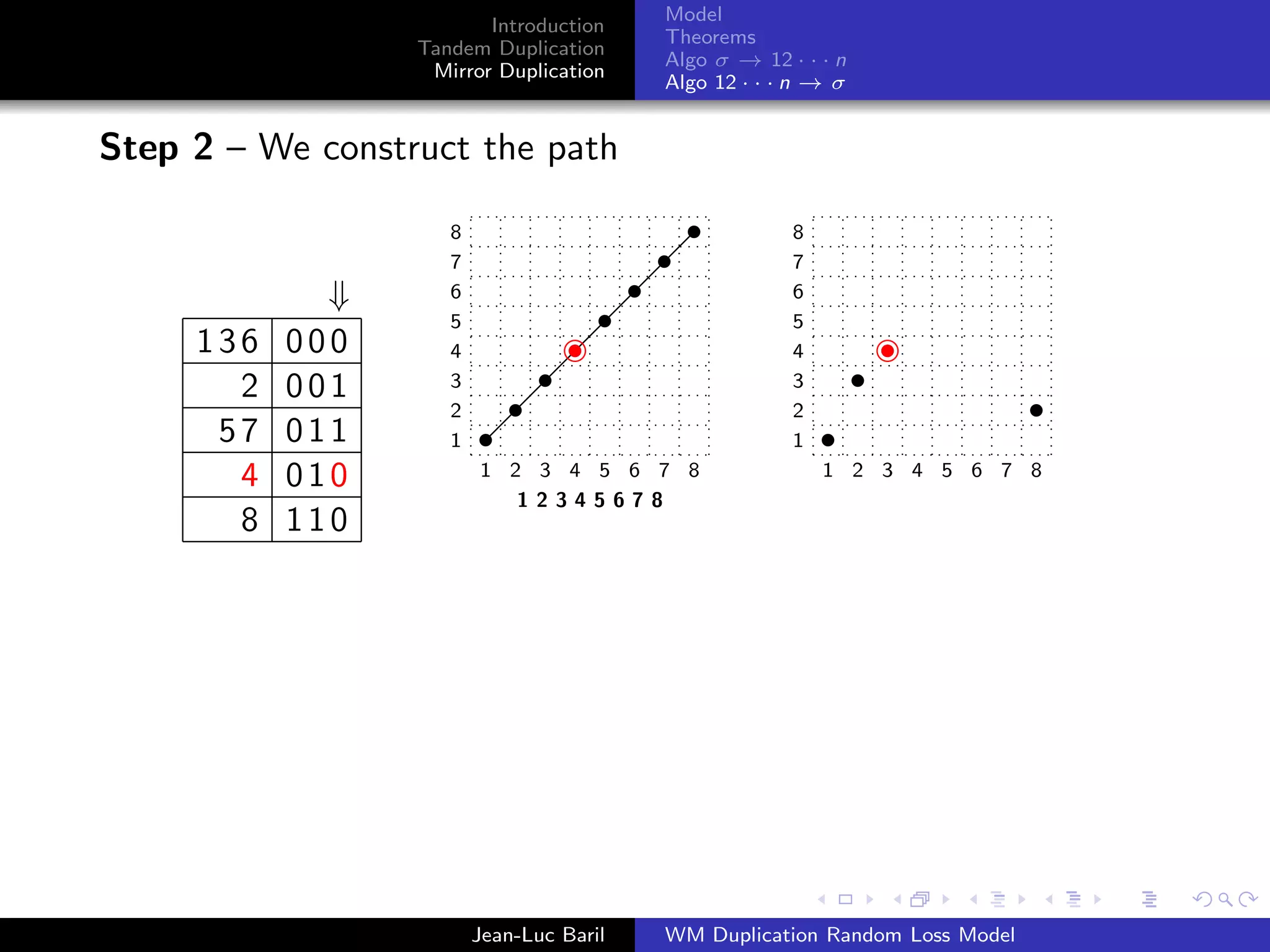
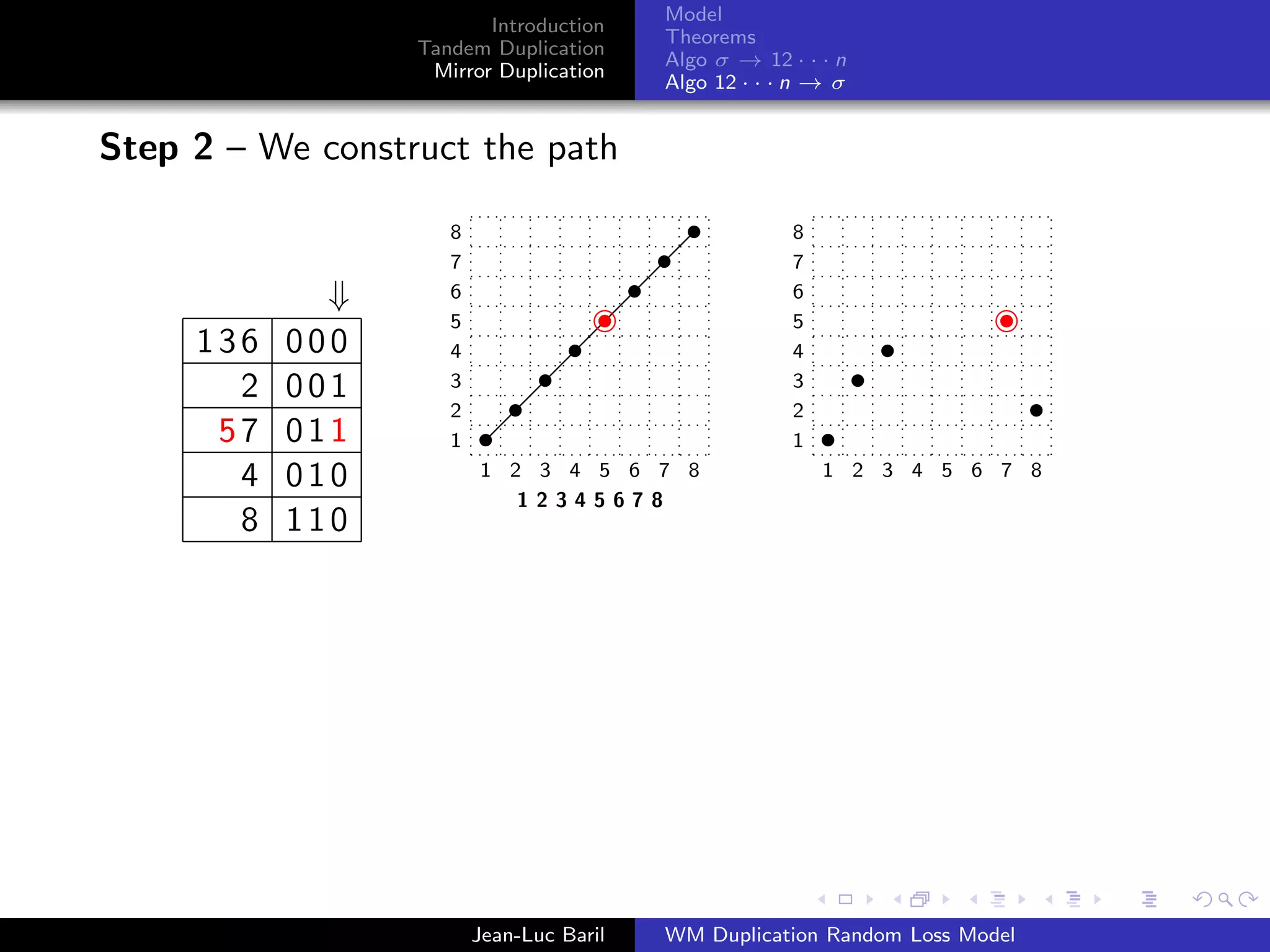
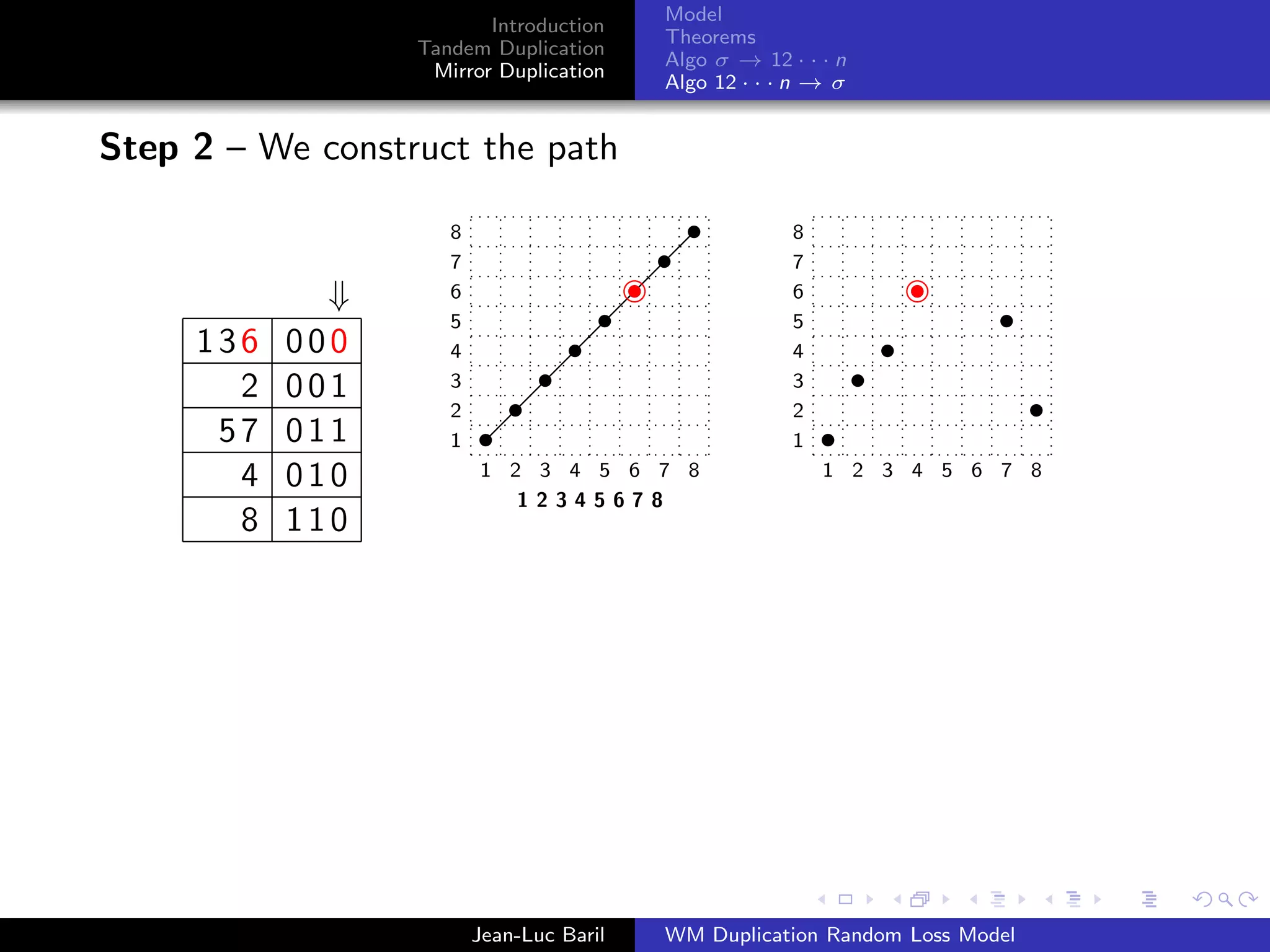
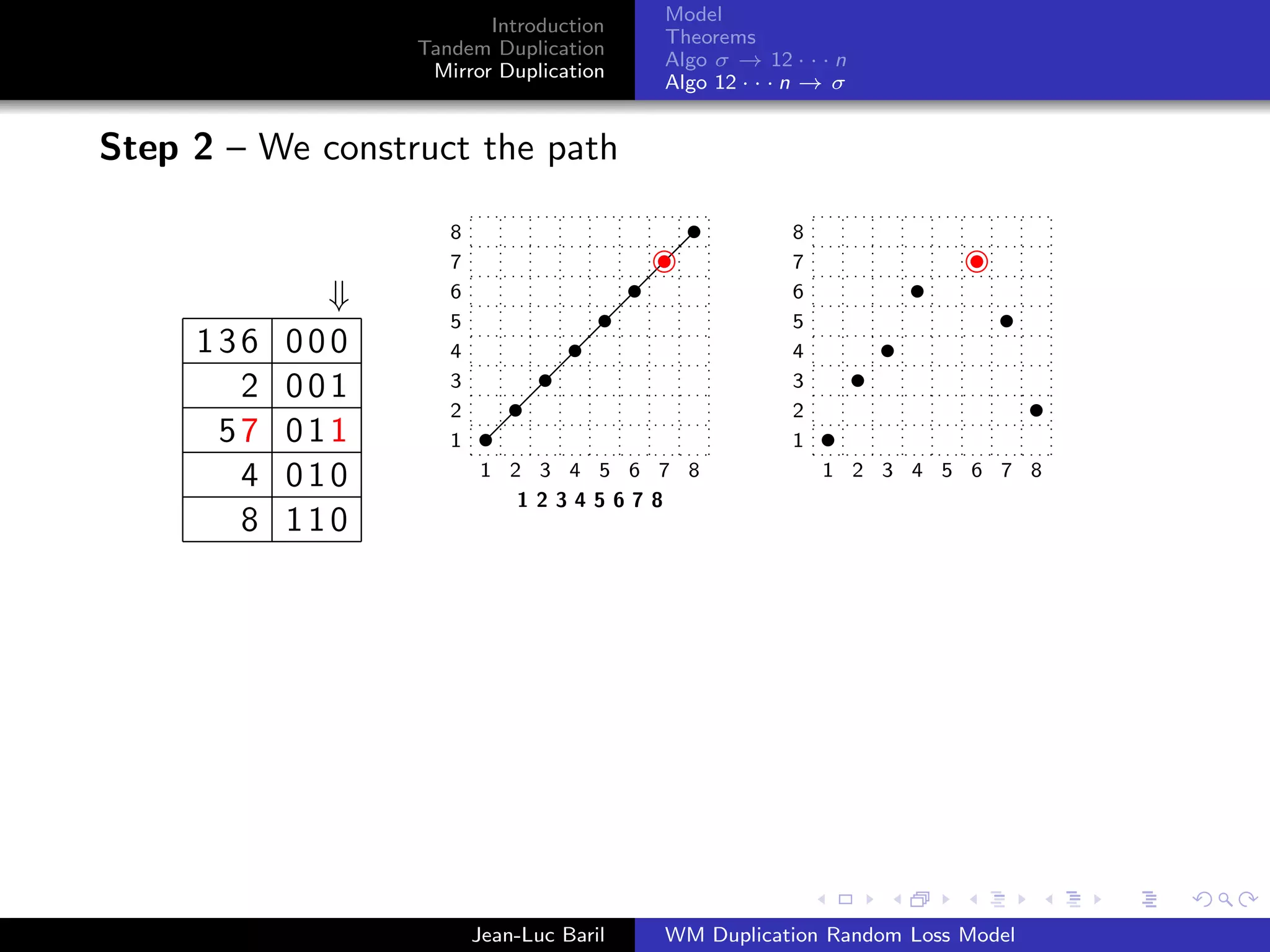
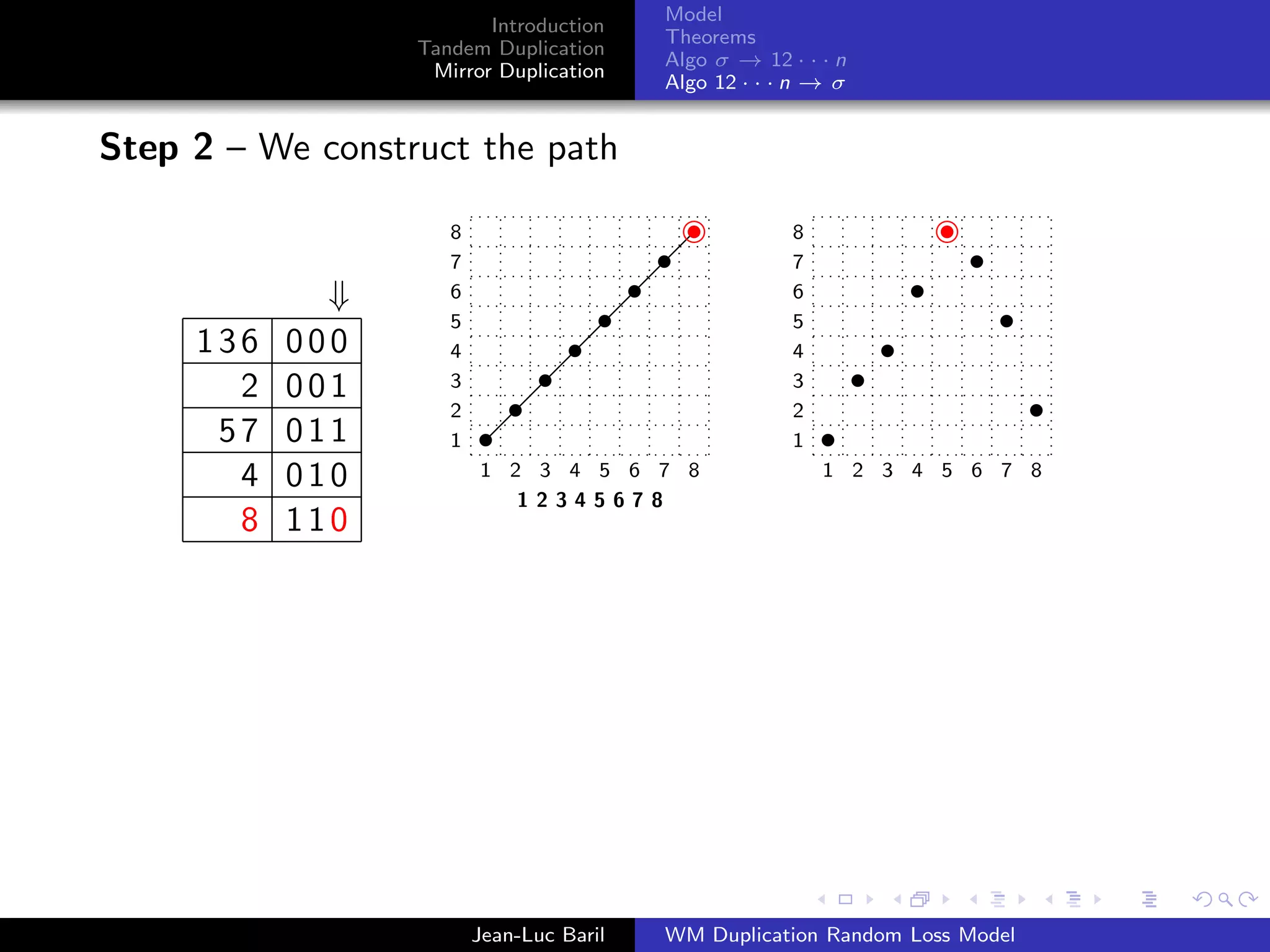
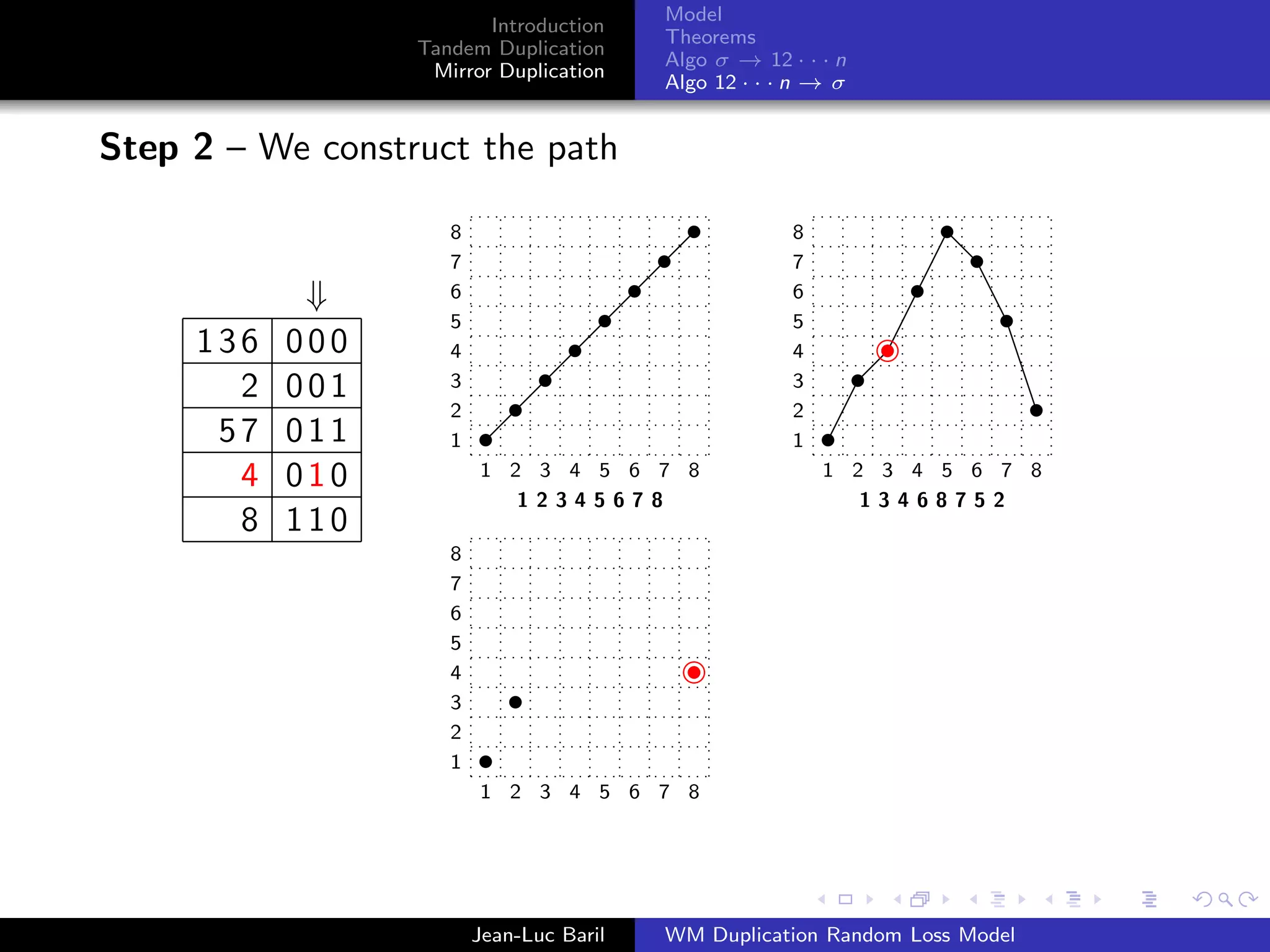
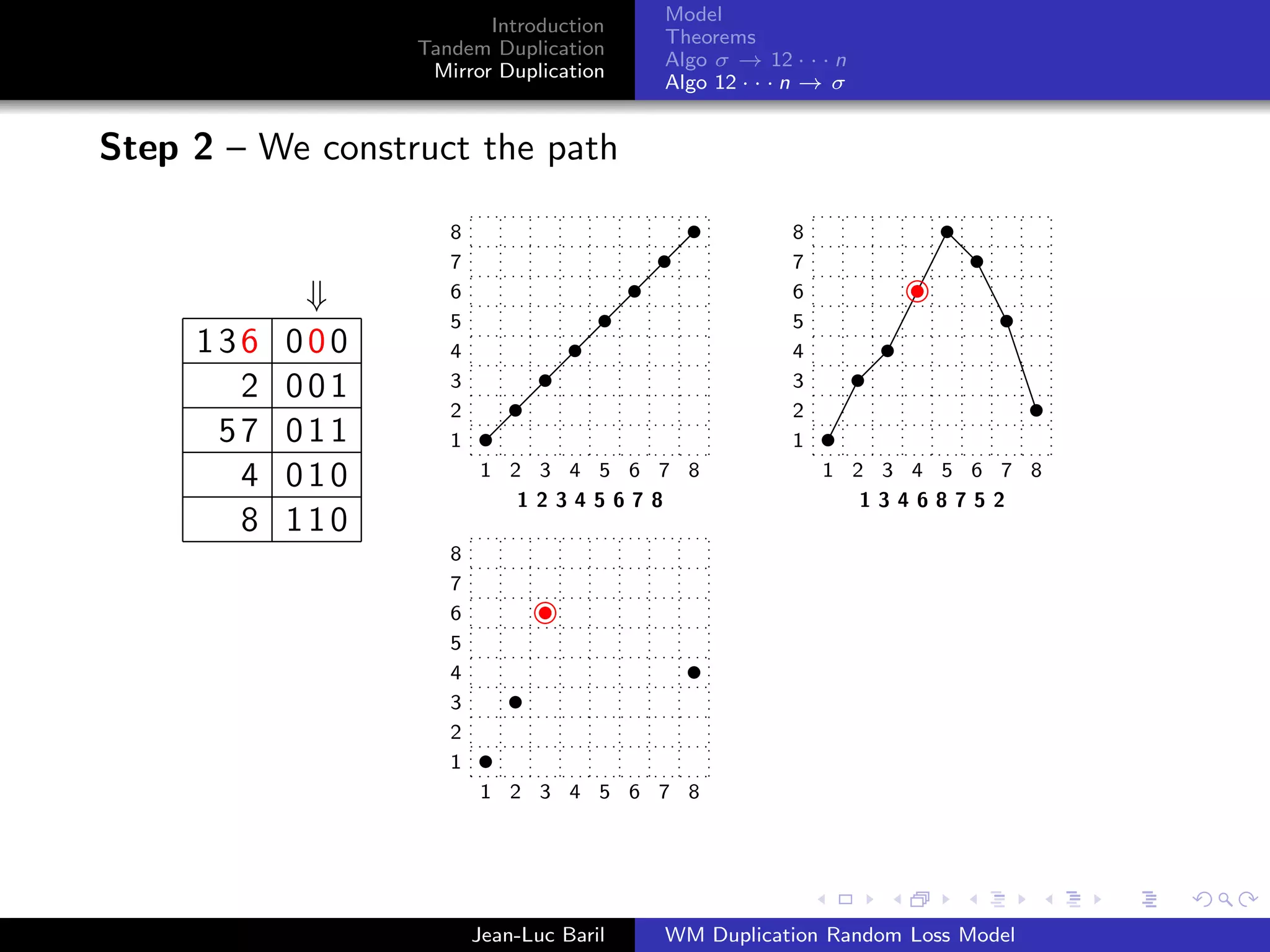
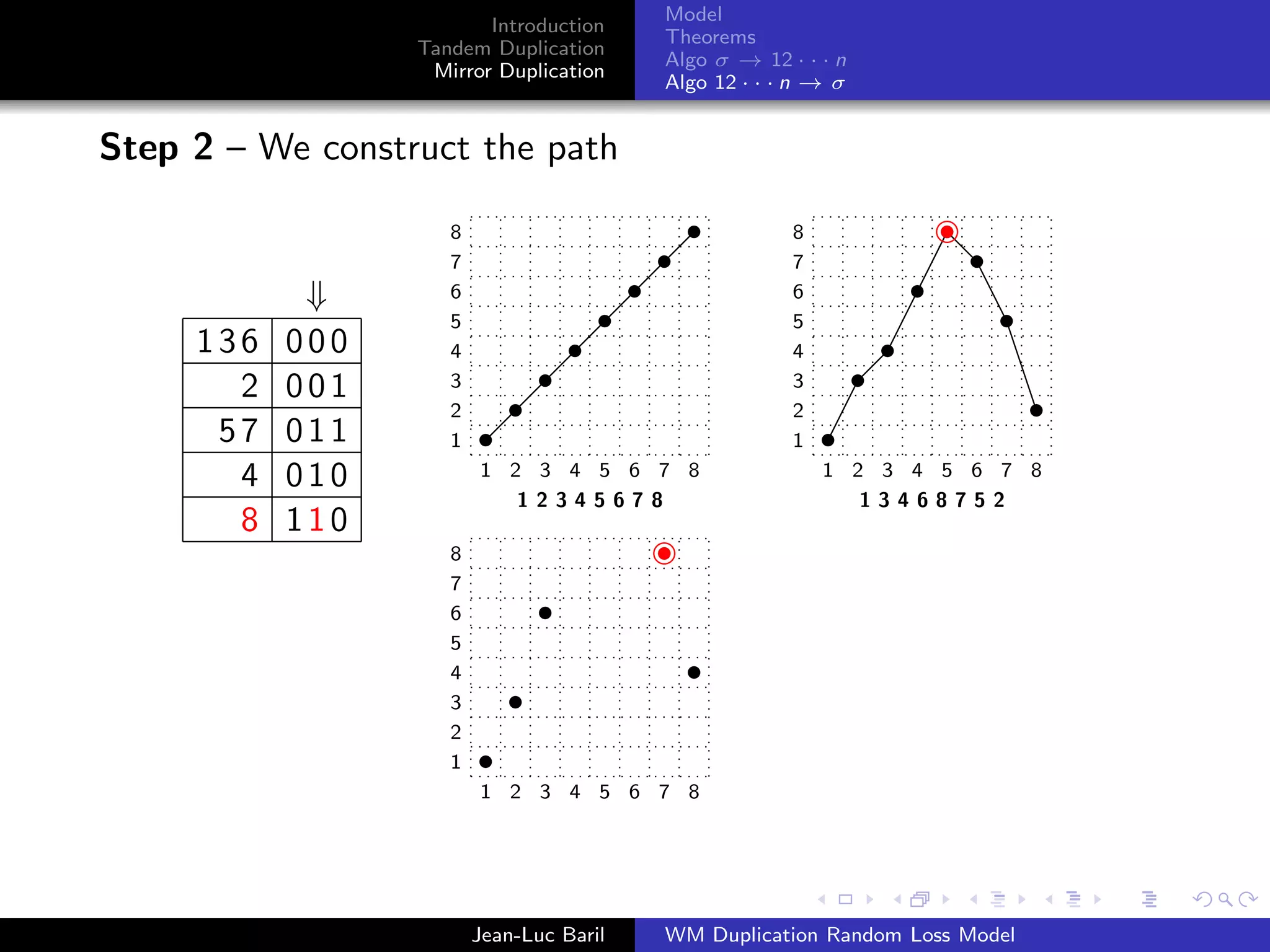
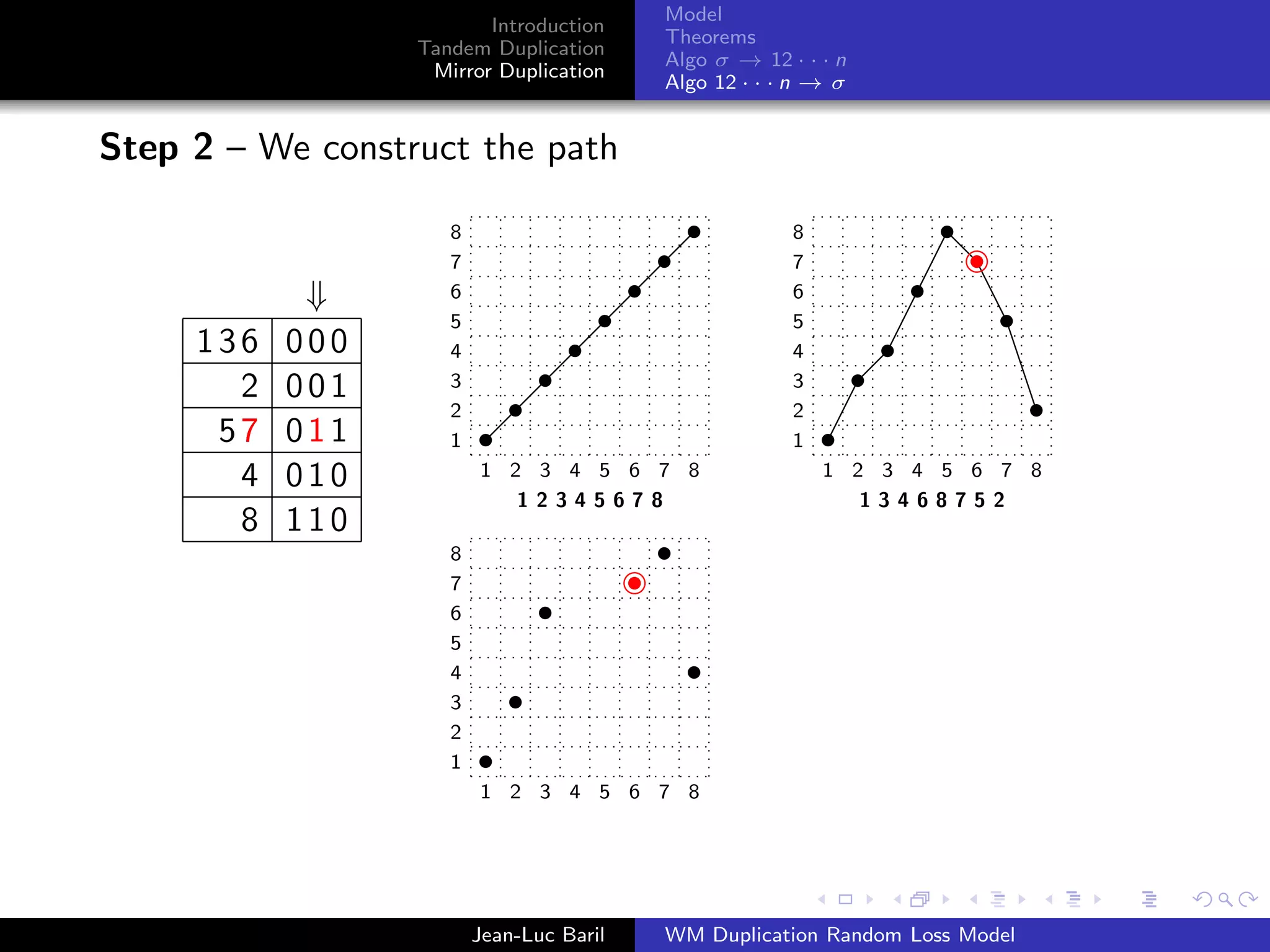
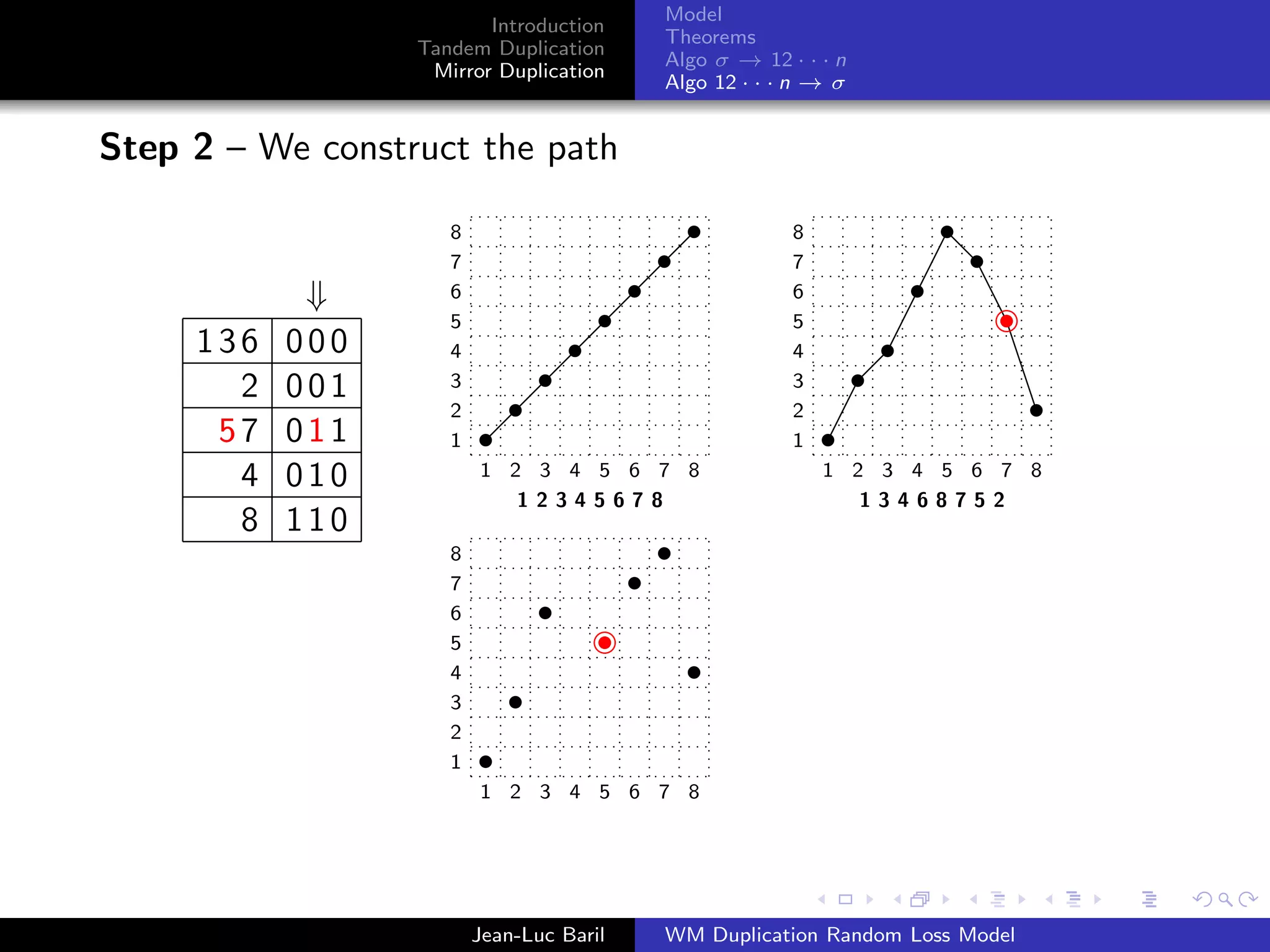
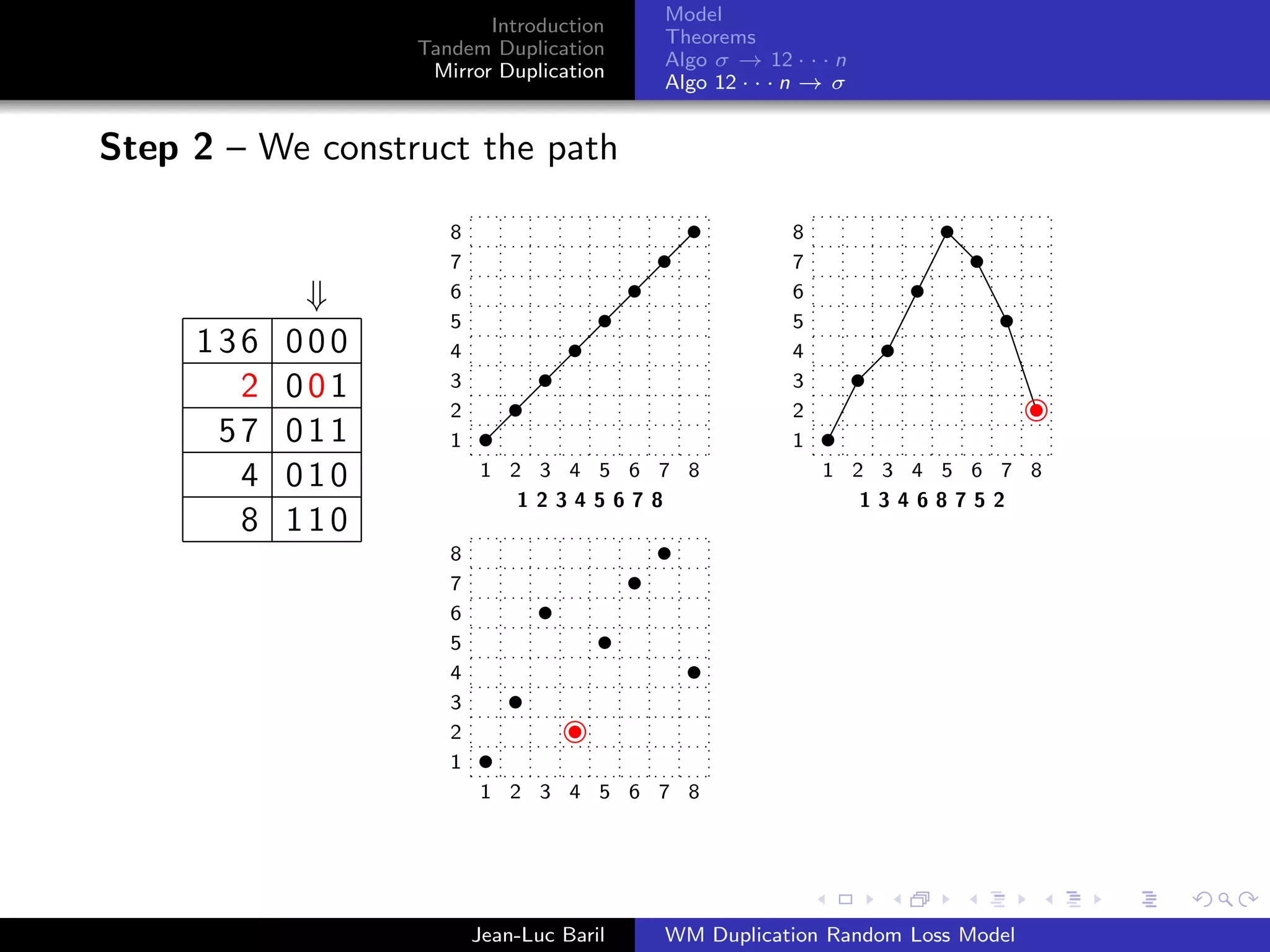
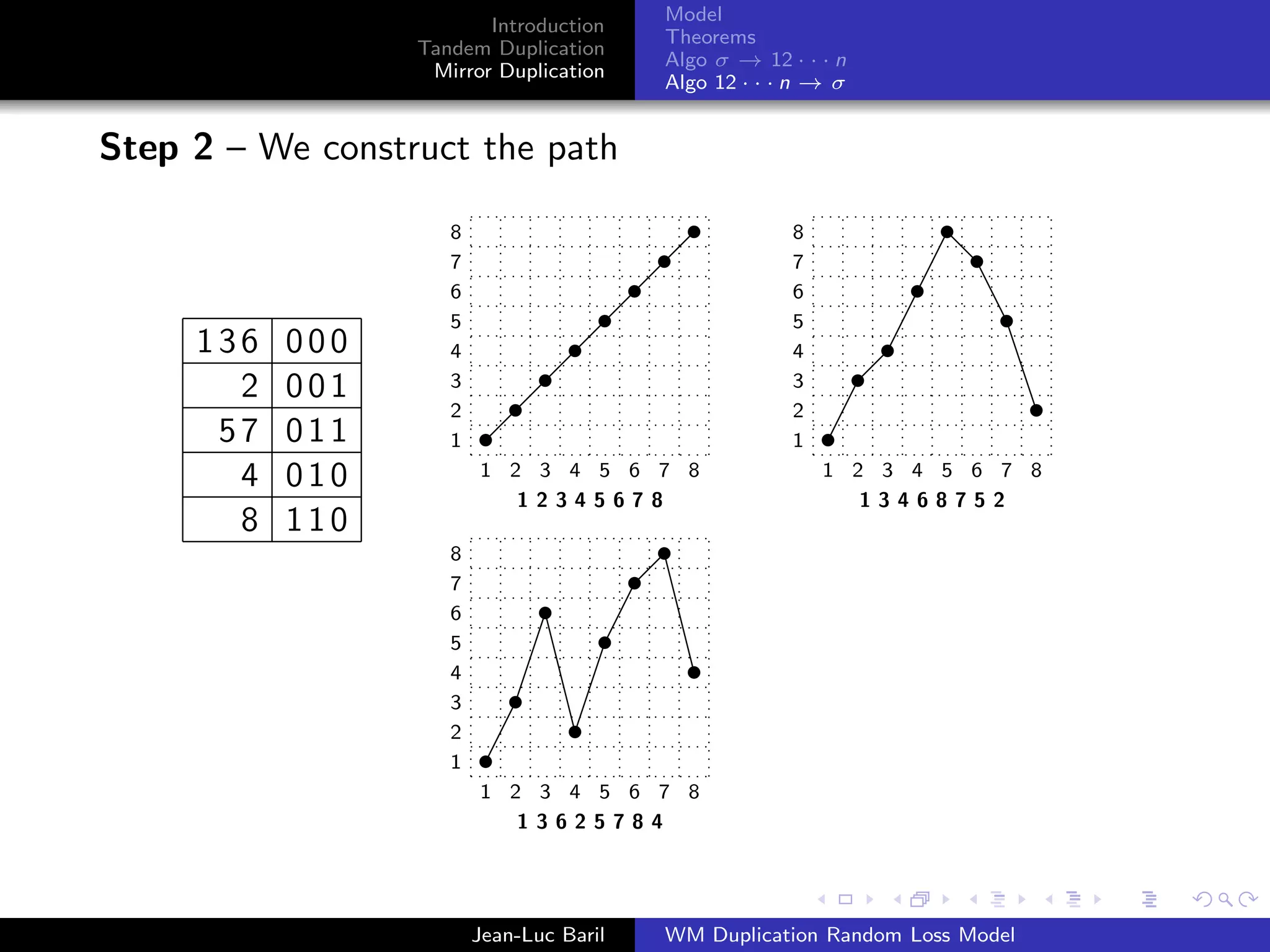
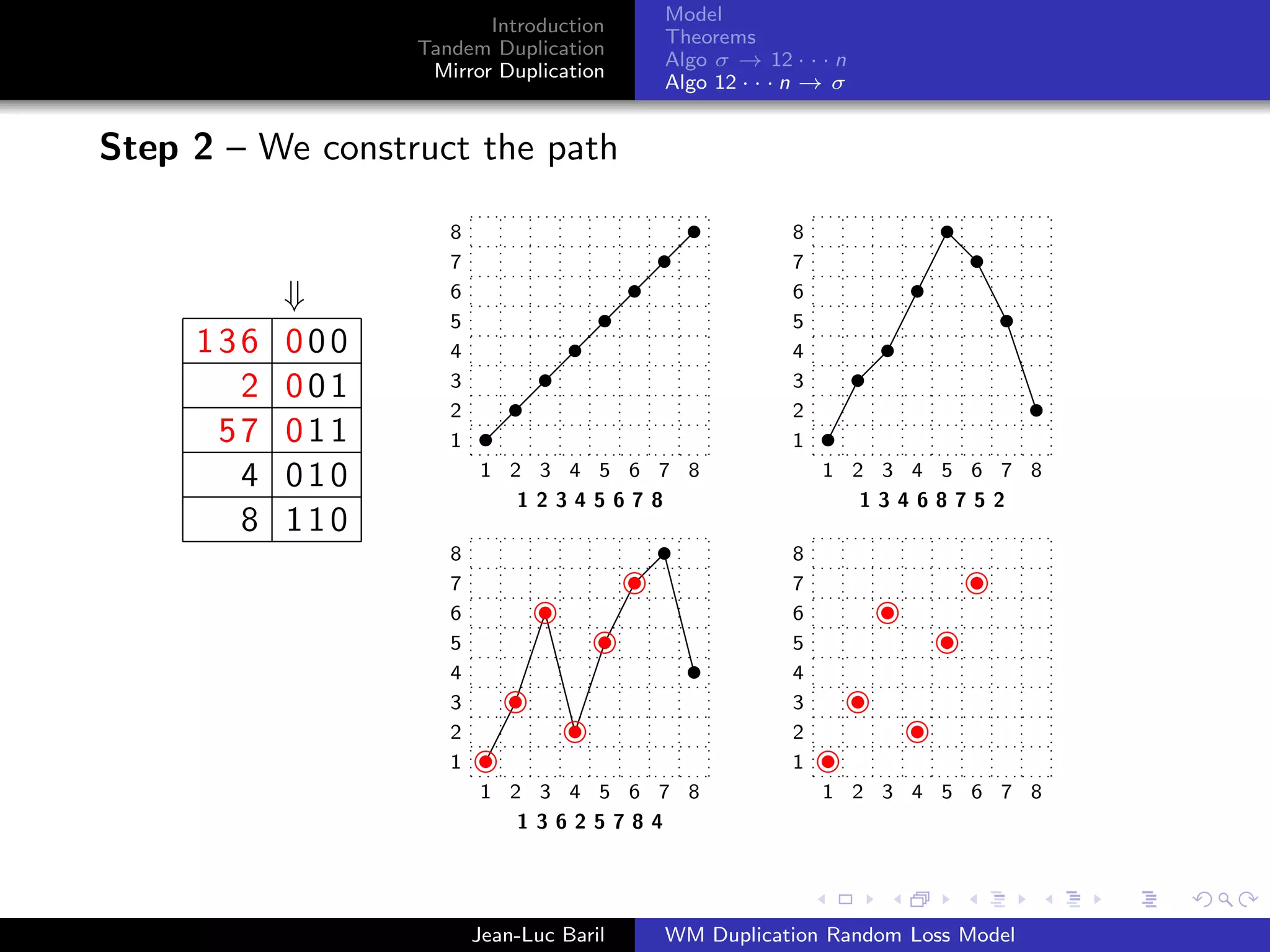
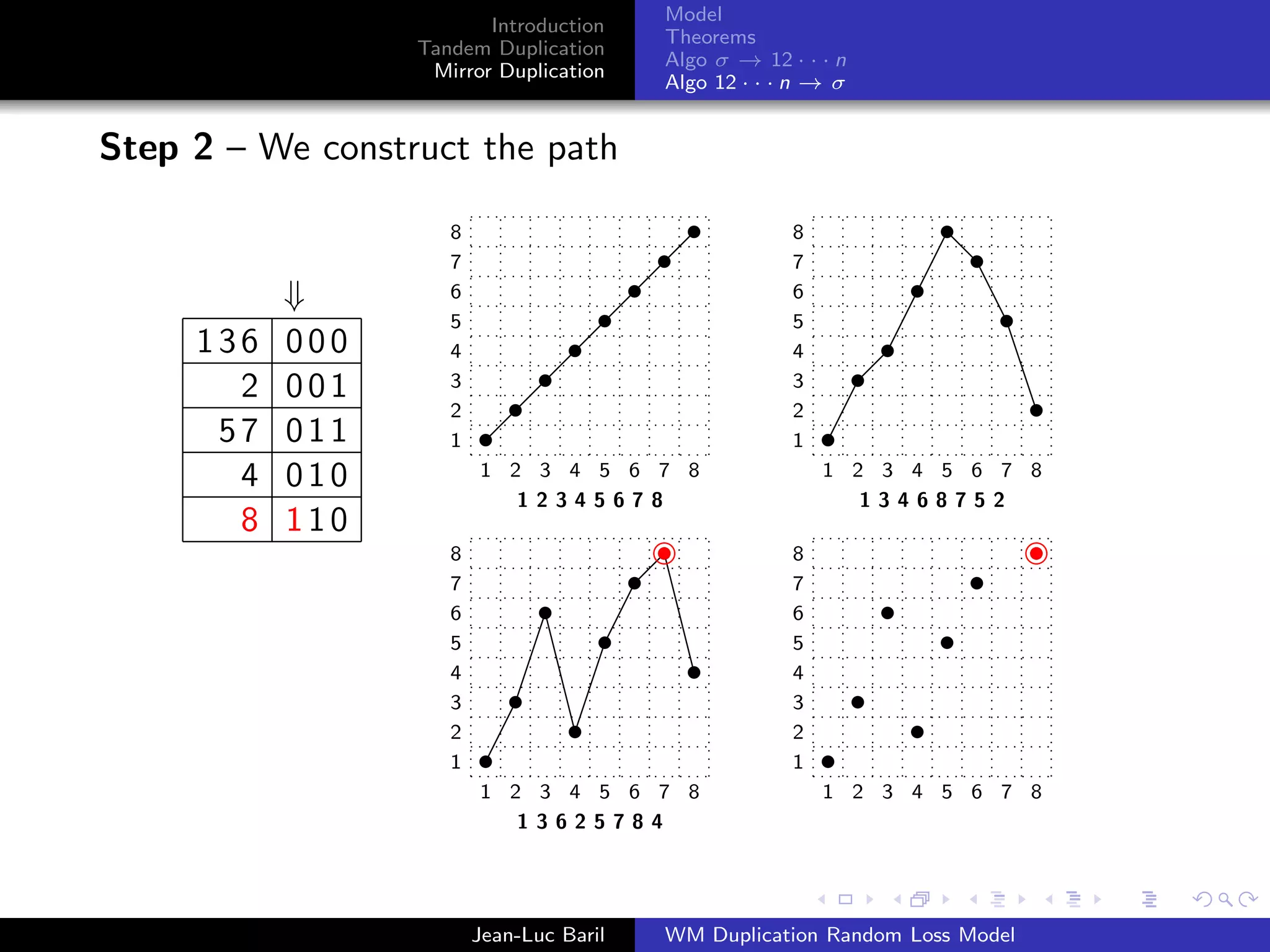
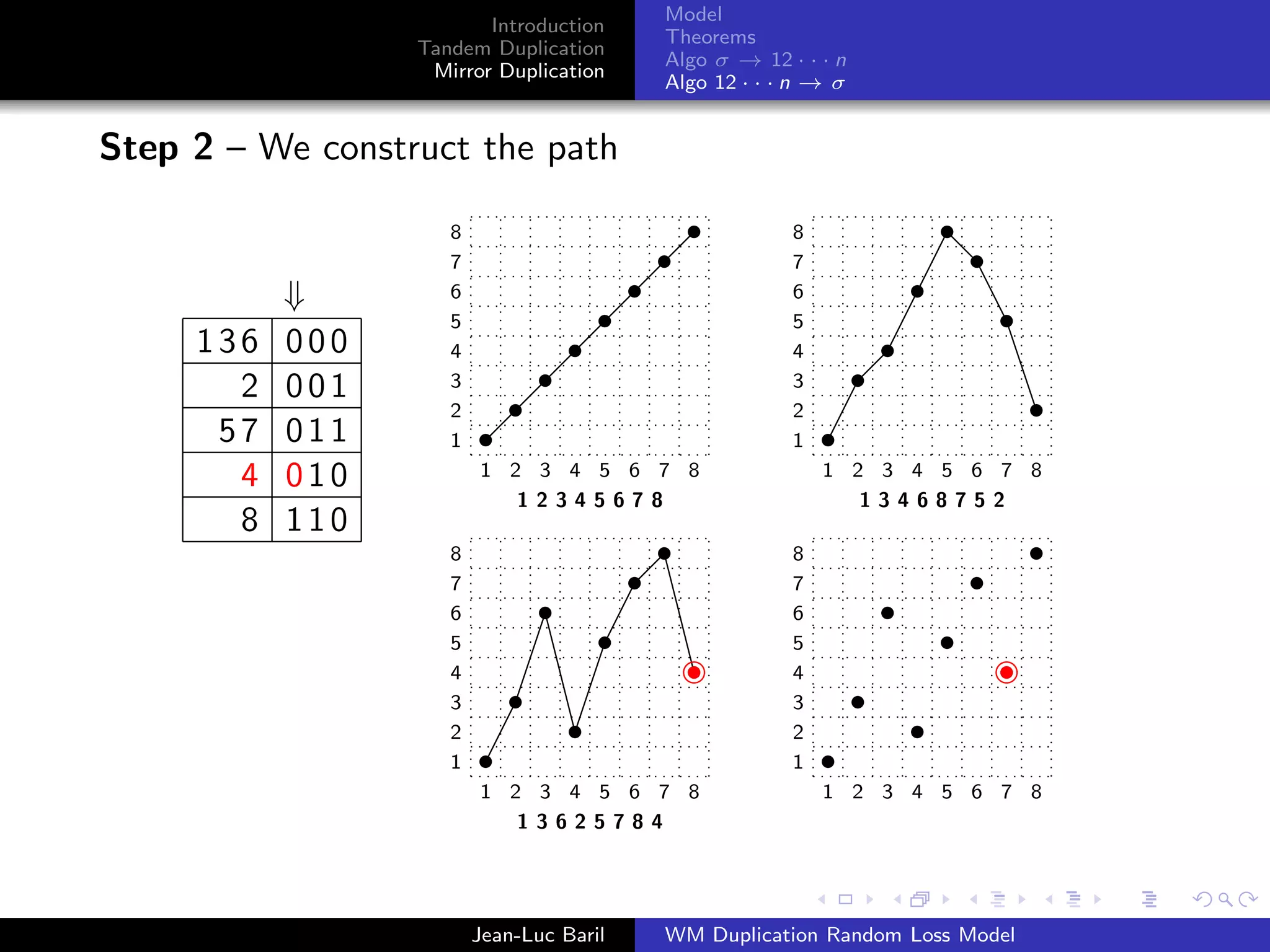
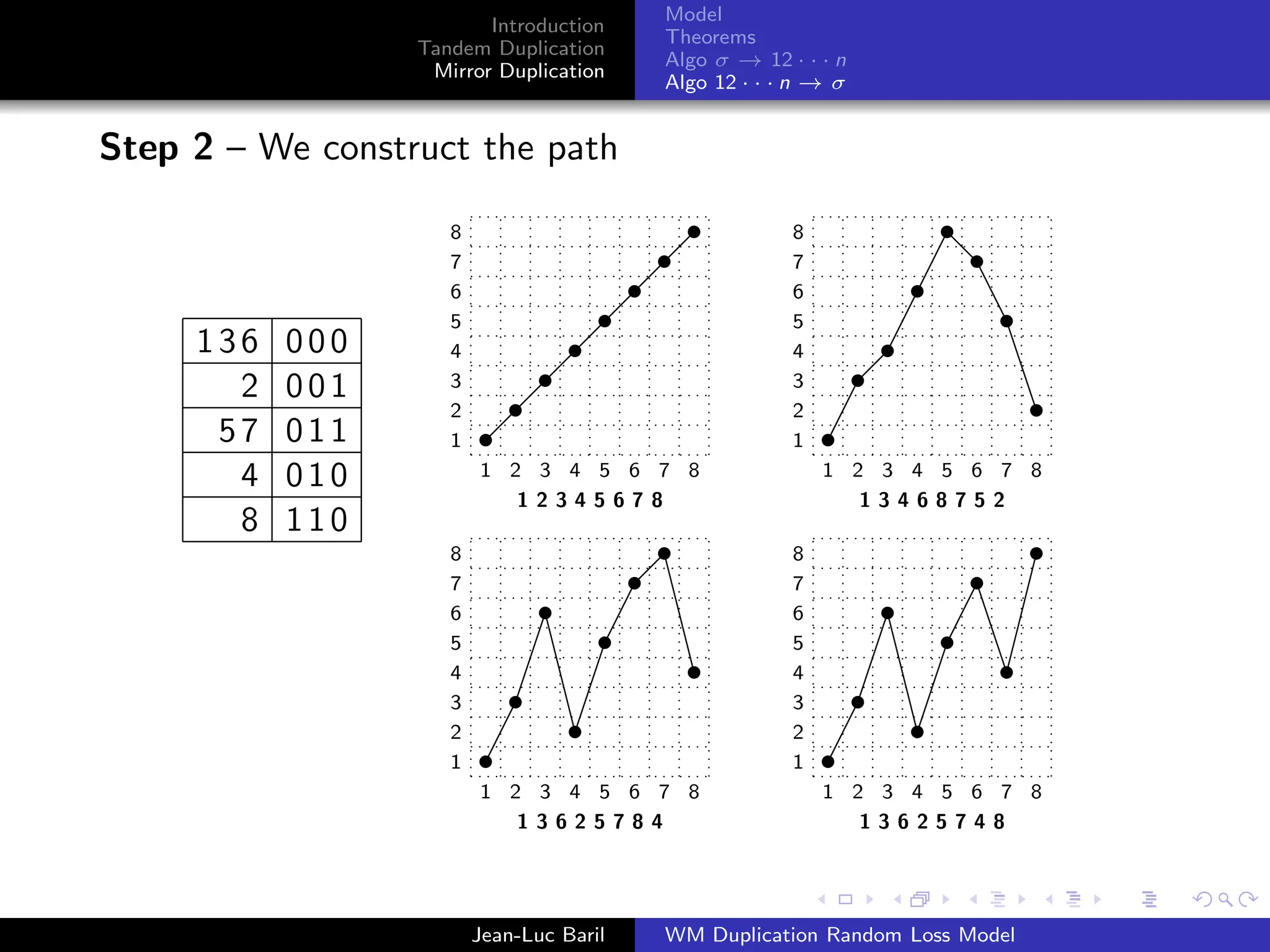
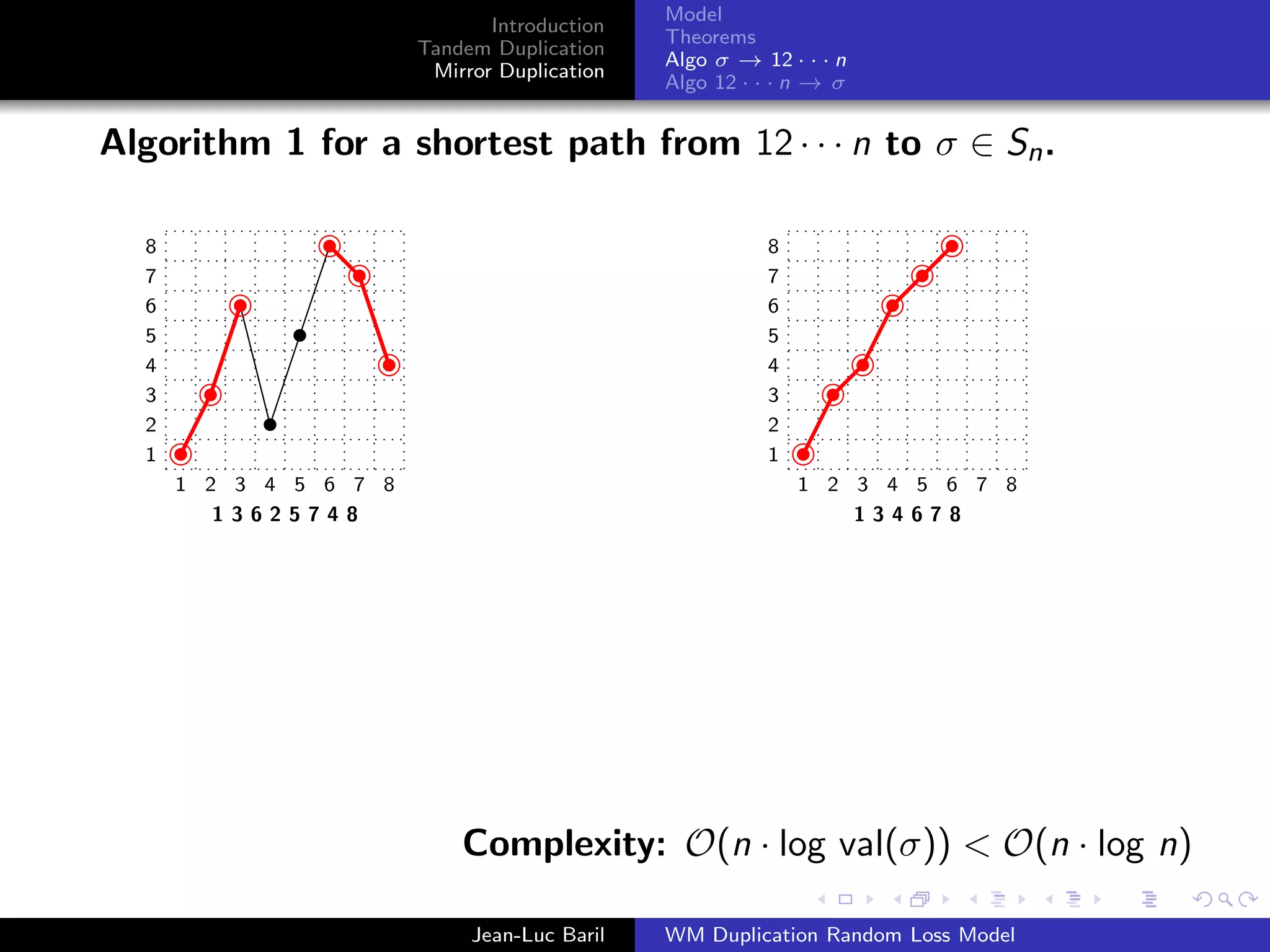
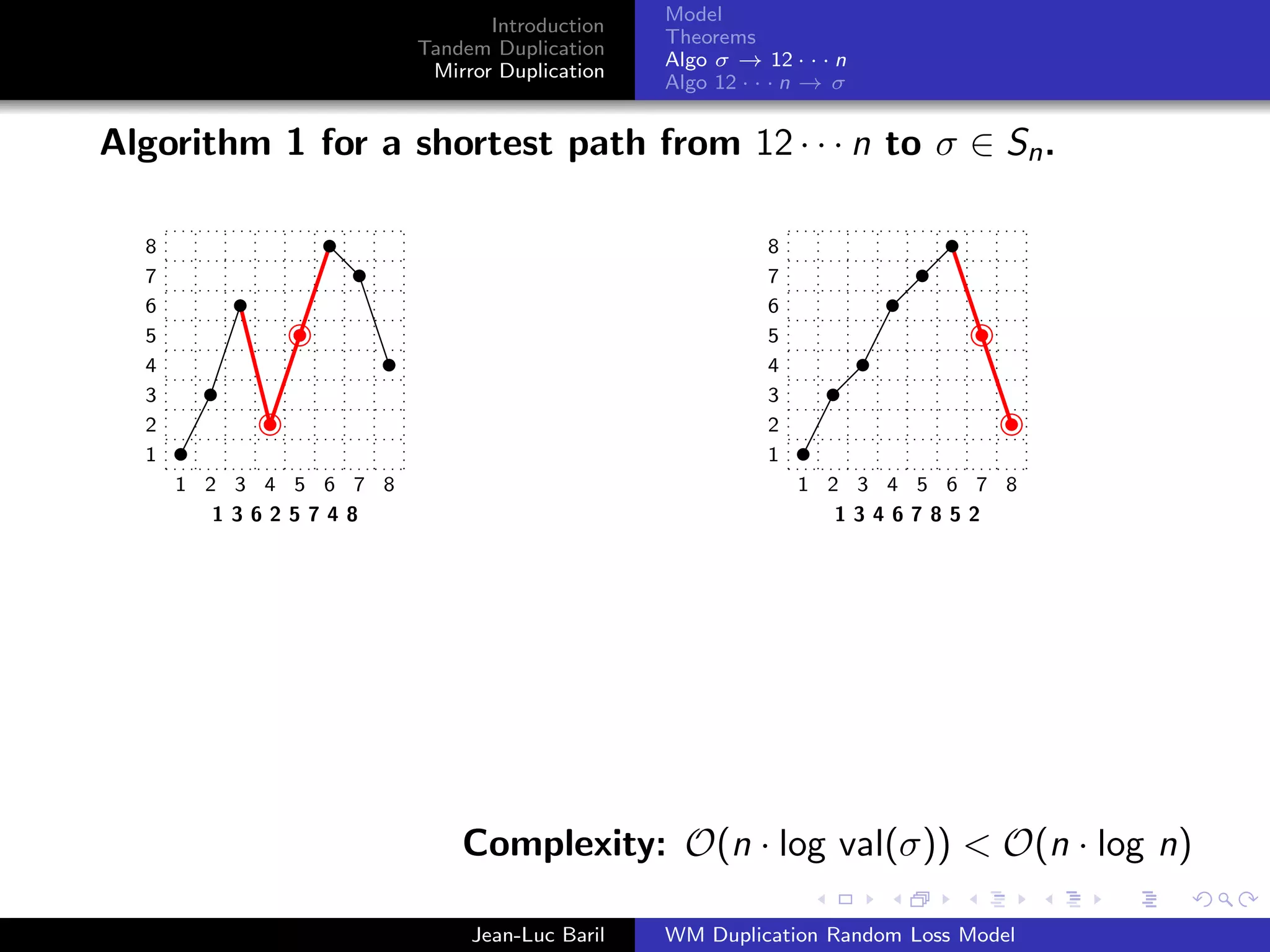
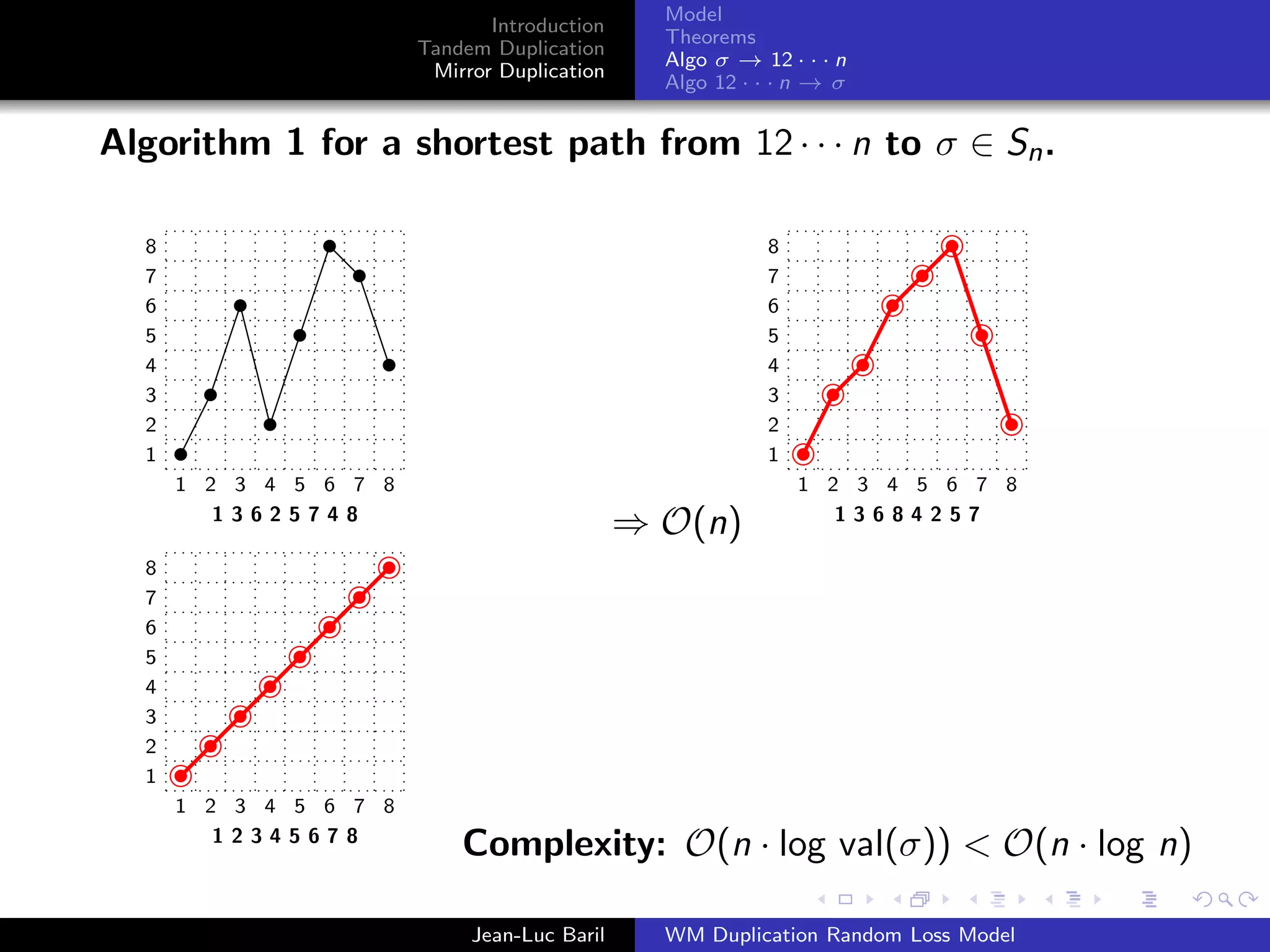
Algorithm 2 for a shortest path from 12 · · · n to σ ∈ Sn .
Step 1 – We label the runs up and runs down with the Binary
Reflected Gray Code (F. Gray [1953], Bitner, Ehrlich, Reingold
[1976])
Bn = 0Bn−1 ◦ 1Bn−1
000
001
011
010
110
111
101
100
Jean-Luc Baril WM Duplication Random Loss Model

36. Model
Introduction
Theorems
Tandem Duplication
Algo σ → 12 · · · n
Mirror Duplication
Algo 12 · · · n → σ
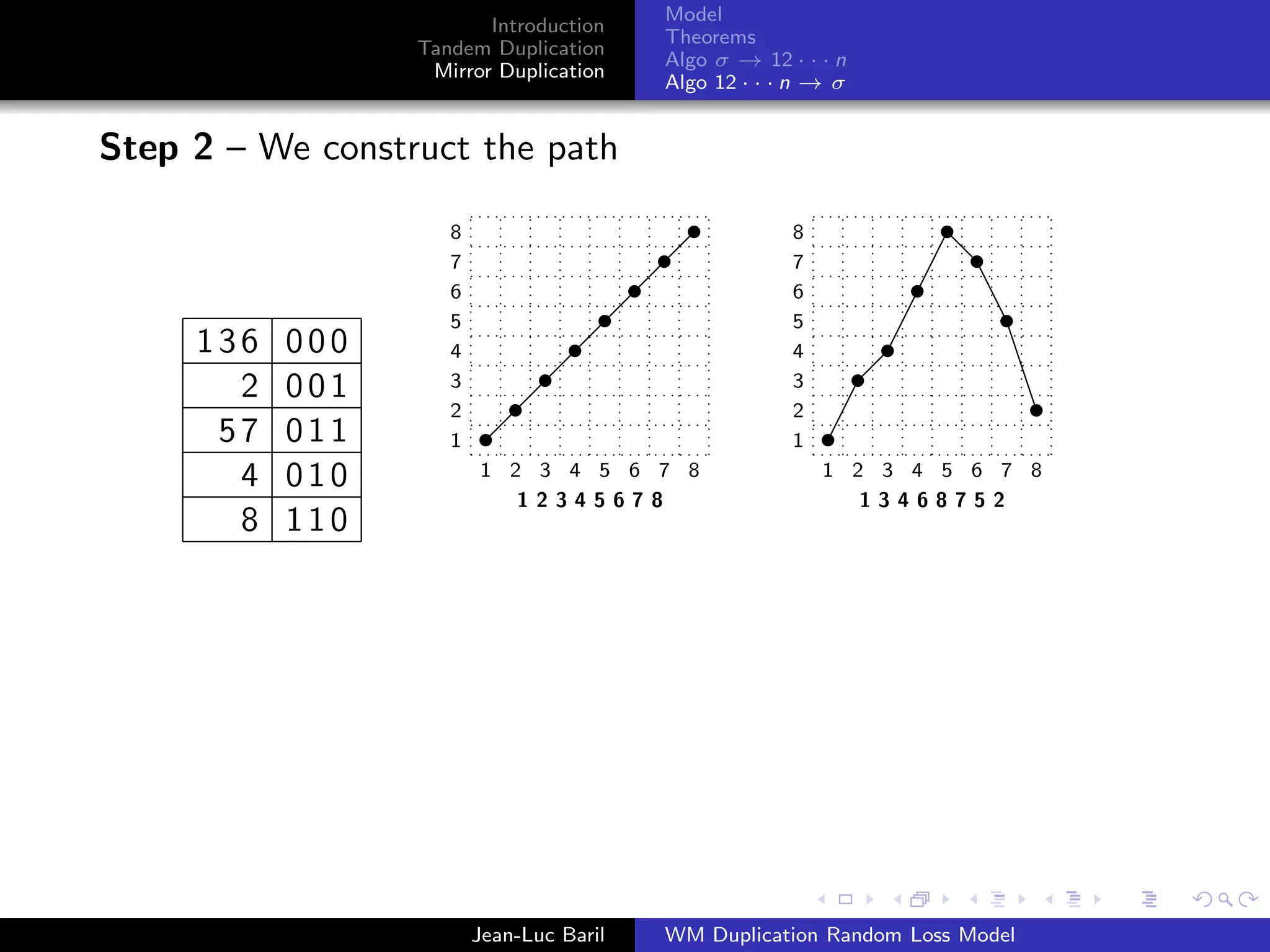
Algorithm 2 for a shortest path from 12 · · · n to σ ∈ Sn .
Step 1 – We label the runs up and runs down with the Binary
Reflected Gray Code (F. Gray [1953], Bitner, Ehrlich, Reingold
[1976])
Bn = 0Bn−1 ◦ 1Bn−1
8
000
7 001
6
5 011
4 010
3
2 110
1
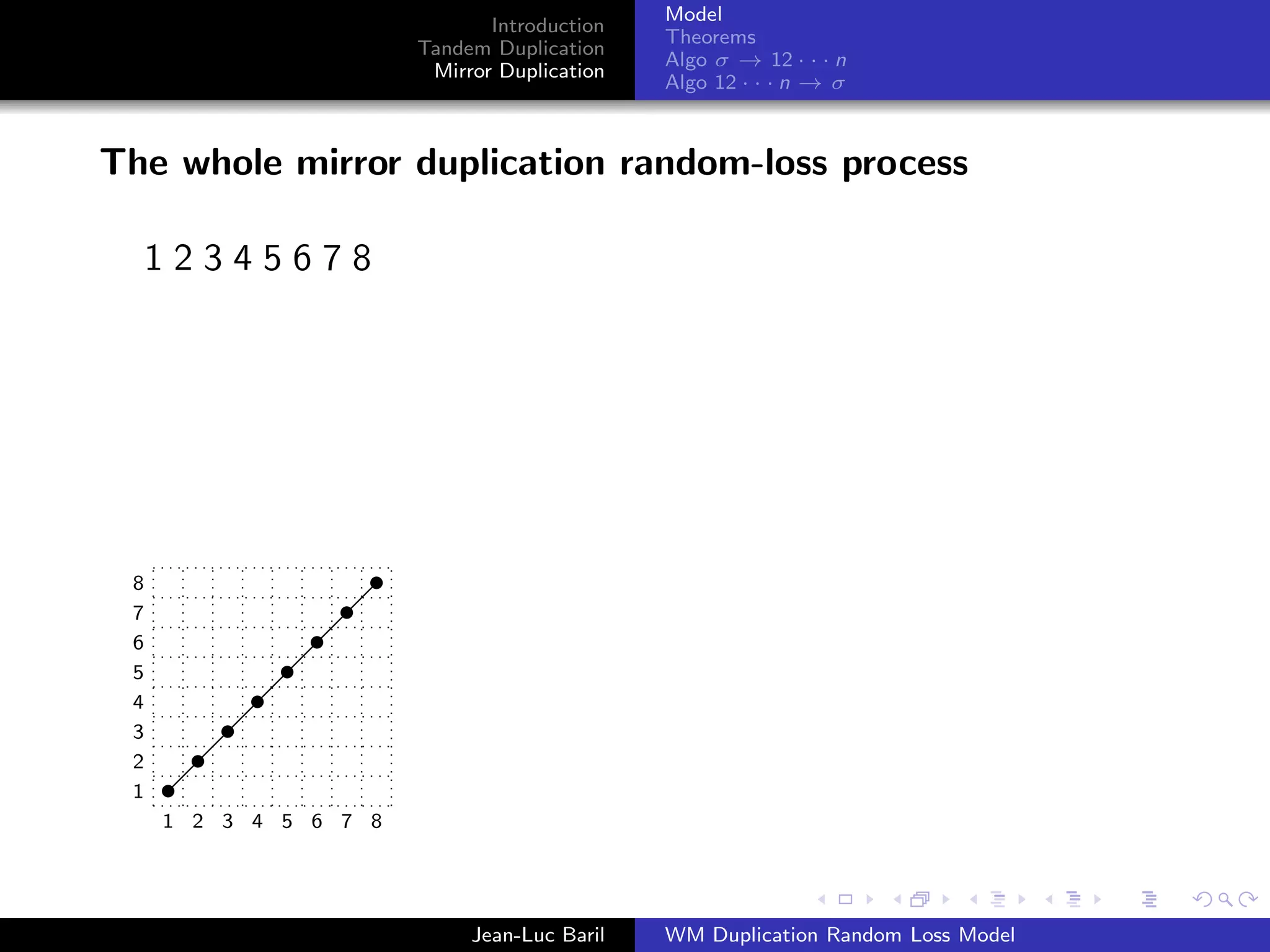
1 2 3 4 5 6 7 8
111
101
100
Jean-Luc Baril WM Duplication Random Loss Model

37. Model
Introduction
Theorems
Tandem Duplication
Algo σ → 12 · · · n
Mirror Duplication
Algo 12 · · · n → σ
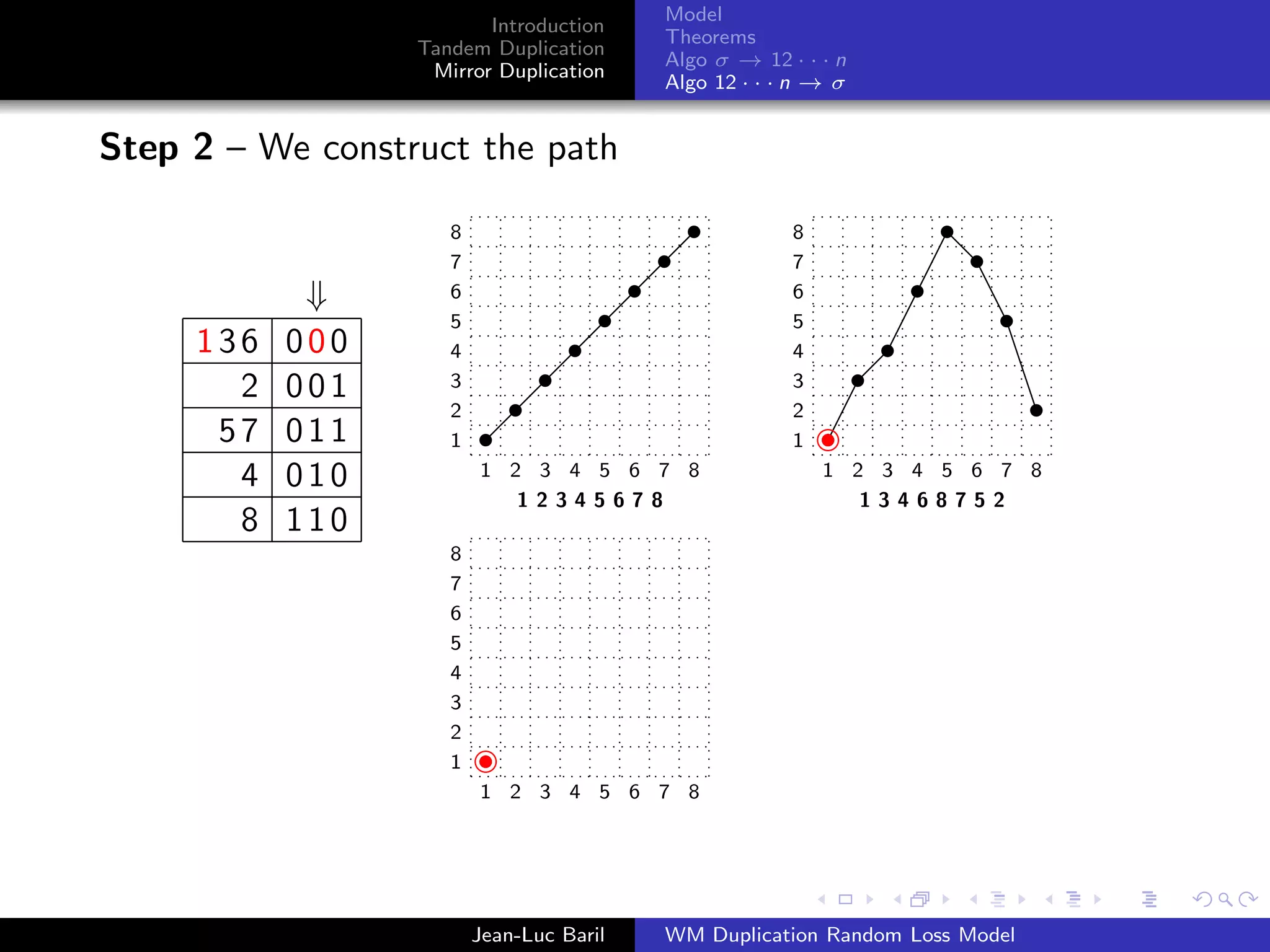
Algorithm 2 for a shortest path from 12 · · · n to σ ∈ Sn .
Step 1 – We label the runs up and runs down with the Binary
Reflected Gray Code (F. Gray [1953], Bitner, Ehrlich, Reingold
[1976])
Bn = 0Bn−1 ◦ 1Bn−1
8
000
7 001
6 136 000
5 011
4 010
3
2 110
1
1 2 3 4 5 6 7 8
111
101
100
Jean-Luc Baril WM Duplication Random Loss Model

38. Model
Introduction
Theorems
Tandem Duplication
Algo σ → 12 · · · n
Mirror Duplication
Algo 12 · · · n → σ
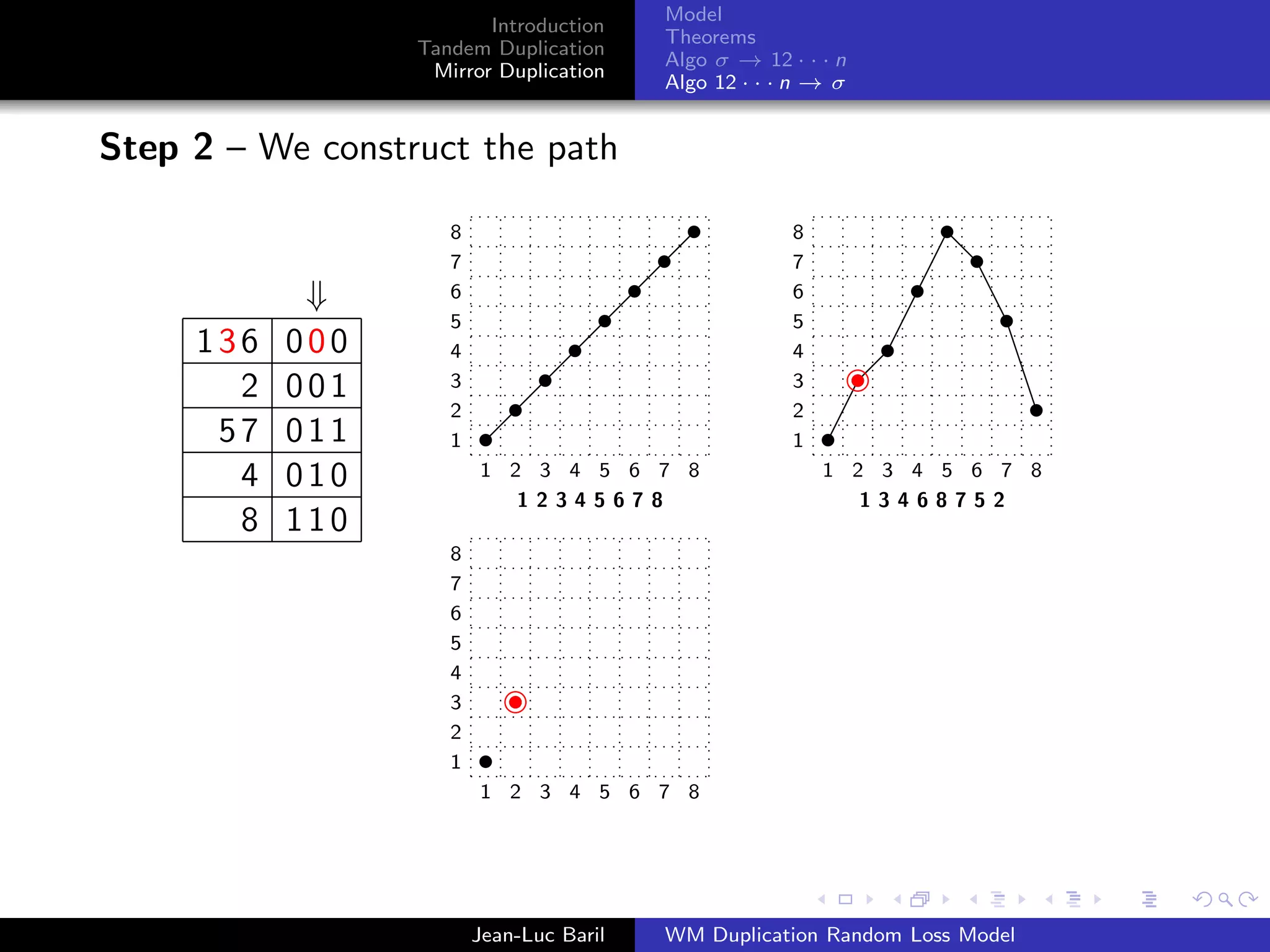
Algorithm 2 for a shortest path from 12 · · · n to σ ∈ Sn .
Step 1 – We label the runs up and runs down with the Binary
Reflected Gray Code (F. Gray [1953], Bitner, Ehrlich, Reingold
[1976])
Bn = 0Bn−1 ◦ 1Bn−1
8
000
7 001
6 136 000
5 011
2 001
4 010
3
2 110
1
1 2 3 4 5 6 7 8
111
101
100
Jean-Luc Baril WM Duplication Random Loss Model

39. Model
Introduction
Theorems
Tandem Duplication
Algo σ → 12 · · · n
Mirror Duplication
Algo 12 · · · n → σ
Algorithm 2 for a shortest path from 12 · · · n to σ ∈ Sn .
Step 1 – We label the runs up and runs down with the Binary
Reflected Gray Code (F. Gray [1953], Bitner, Ehrlich, Reingold
[1976])
Bn = 0Bn−1 ◦ 1Bn−1
8
000
7 001
6 136 000
5 011
2 001
4 010
3 57 011
2 110
1
1 2 3 4 5 6 7 8
111
101
100
Jean-Luc Baril WM Duplication Random Loss Model

40. Model
Introduction
Theorems
Tandem Duplication
Algo σ → 12 · · · n
Mirror Duplication
Algo 12 · · · n → σ
Algorithm 2 for a shortest path from 12 · · · n to σ ∈ Sn .
Step 1 – We label the runs up and runs down with the Binary
Reflected Gray Code (F. Gray [1953], Bitner, Ehrlich, Reingold
[1976])
Bn = 0Bn−1 ◦ 1Bn−1
8
000
7 001
6 136 000
5 011
2 001
4 010
3 57 011
2
4 010 110
1
1 2 3 4 5 6 7 8
111
101
100
Jean-Luc Baril WM Duplication Random Loss Model

41. Model
Introduction
Theorems
Tandem Duplication
Algo σ → 12 · · · n
Mirror Duplication
Algo 12 · · · n → σ
Algorithm 2 for a shortest path from 12 · · · n to σ ∈ Sn .
Step 1 – We label the runs up and runs down with the Binary
Reflected Gray Code (F. Gray [1953], Bitner, Ehrlich, Reingold
[1976])
Bn = 0Bn−1 ◦ 1Bn−1
8
000
7 001
6 136 000
5 011
2 001
4 010
3 57 011
2
4 010 110
1
1 2 3 4 5 6 7 8 8 110 111
101
100
Jean-Luc Baril WM Duplication Random Loss Model

42. Model
Introduction
Theorems
Tandem Duplication
Algo σ → 12 · · · n
Mirror Duplication
Algo 12 · · · n → σ
Step 2 – We construct the path
8
7
6
5
136 000 4
2 001 3
2
57 011 1
4 010 1 2 3 4 5 6 7 8
12345678
8 110
Jean-Luc Baril WM Duplication Random Loss Model

43. Model
Introduction
Theorems
Tandem Duplication
Algo σ → 12 · · · n
Mirror Duplication
Algo 12 · · · n → σ
Step 2 – We construct the path
8 8
7 7
⇓ 6 6
5 5
136 000 4 4
2 001 3 3
2 2
57 011 1 1
4 010 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8
12345678
8 110
Jean-Luc Baril WM Duplication Random Loss Model

44. Model
Introduction
Theorems
Tandem Duplication
Algo σ → 12 · · · n
Mirror Duplication
Algo 12 · · · n → σ
Step 2 – We construct the path
8 8
7 7
⇓ 6 6
5 5
136 000 4 4
2 001 3 3
2 2
57 011 1 1
4 010 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8
12345678
8 110
Jean-Luc Baril WM Duplication Random Loss Model

45. Model
Introduction
Theorems
Tandem Duplication
Algo σ → 12 · · · n
Mirror Duplication
Algo 12 · · · n → σ
Step 2 – We construct the path
8 8
7 7
⇓ 6 6
5 5
136 000 4 4
2 001 3 3
2 2
57 011 1 1
4 010 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8
12345678
8 110
Jean-Luc Baril WM Duplication Random Loss Model

46. Model
Introduction
Theorems
Tandem Duplication
Algo σ → 12 · · · n
Mirror Duplication
Algo 12 · · · n → σ
Step 2 – We construct the path
8 8
7 7
⇓ 6 6
5 5
136 000 4 4
2 001 3 3
2 2
57 011 1 1
4 010 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8
12345678
8 110
Jean-Luc Baril WM Duplication Random Loss Model

47. Model
Introduction
Theorems
Tandem Duplication
Algo σ → 12 · · · n
Mirror Duplication
Algo 12 · · · n → σ
Step 2 – We construct the path
8 8
7 7
⇓ 6 6
5 5
136 000 4 4
2 001 3 3
2 2
57 011 1 1
4 010 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8
12345678
8 110
Jean-Luc Baril WM Duplication Random Loss Model

48. Model
Introduction
Theorems
Tandem Duplication
Algo σ → 12 · · · n
Mirror Duplication
Algo 12 · · · n → σ
Step 2 – We construct the path
8 8
7 7
⇓ 6 6
5 5
136 000 4 4
2 001 3 3
2 2
57 011 1 1
4 010 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8
12345678
8 110
Jean-Luc Baril WM Duplication Random Loss Model

49. Model
Introduction
Theorems
Tandem Duplication
Algo σ → 12 · · · n
Mirror Duplication
Algo 12 · · · n → σ
Step 2 – We construct the path
8 8
7 7
⇓ 6 6
5 5
136 000 4 4
2 001 3 3
2 2
57 011 1 1
4 010 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8
12345678
8 110
Jean-Luc Baril WM Duplication Random Loss Model

50. Model
Introduction
Theorems
Tandem Duplication
Algo σ → 12 · · · n
Mirror Duplication
Algo 12 · · · n → σ
Step 2 – We construct the path
8 8
7 7
⇓ 6 6
5 5
136 000 4 4
2 001 3 3
2 2
57 011 1 1
4 010 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8
12345678
8 110
Jean-Luc Baril WM Duplication Random Loss Model

51. Model
Introduction
Theorems
Tandem Duplication
Algo σ → 12 · · · n
Mirror Duplication
Algo 12 · · · n → σ
Step 2 – We construct the path
8 8
7 7
6 6
5 5
136 000 4 4
2 001 3 3
2 2
57 011 1 1
4 010 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8
12345678 13468752
8 110
Jean-Luc Baril WM Duplication Random Loss Model

52. Model
Introduction
Theorems
Tandem Duplication
Algo σ → 12 · · · n
Mirror Duplication
Algo 12 · · · n → σ
Step 2 – We construct the path
8 8
7 7
⇓ 6 6
5 5
136 000 4 4
2 001 3 3
2 2
57 011 1 1
4 010 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8
12345678 13468752
8 110
8
7
6
5
4
3
2
1
1 2 3 4 5 6 7 8
Jean-Luc Baril WM Duplication Random Loss Model

53. Model
Introduction
Theorems
Tandem Duplication
Algo σ → 12 · · · n
Mirror Duplication
Algo 12 · · · n → σ
Step 2 – We construct the path
8 8
7 7
⇓ 6 6
5 5
136 000 4 4
2 001 3 3
2 2
57 011 1 1
4 010 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8
12345678 13468752
8 110
8
7
6
5
4
3
2
1
1 2 3 4 5 6 7 8
Jean-Luc Baril WM Duplication Random Loss Model

54. Model
Introduction
Theorems
Tandem Duplication
Algo σ → 12 · · · n
Mirror Duplication
Algo 12 · · · n → σ
Step 2 – We construct the path
8 8
7 7
⇓ 6 6
5 5
136 000 4 4
2 001 3 3
2 2
57 011 1 1
4 010 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8
12345678 13468752
8 110
8
7
6
5
4
3
2
1
1 2 3 4 5 6 7 8
Jean-Luc Baril WM Duplication Random Loss Model

55. Model
Introduction
Theorems
Tandem Duplication
Algo σ → 12 · · · n
Mirror Duplication
Algo 12 · · · n → σ
Step 2 – We construct the path
8 8
7 7
⇓ 6 6
5 5
136 000 4 4
2 001 3 3
2 2
57 011 1 1
4 010 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8
12345678 13468752
8 110
8
7
6
5
4
3
2
1
1 2 3 4 5 6 7 8
Jean-Luc Baril WM Duplication Random Loss Model

56. Model
Introduction
Theorems
Tandem Duplication
Algo σ → 12 · · · n
Mirror Duplication
Algo 12 · · · n → σ
Step 2 – We construct the path
8 8
7 7
⇓ 6 6
5 5
136 000 4 4
2 001 3 3
2 2
57 011 1 1
4 010 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8
12345678 13468752
8 110
8
7
6
5
4
3
2
1
1 2 3 4 5 6 7 8
Jean-Luc Baril WM Duplication Random Loss Model

57. Model
Introduction
Theorems
Tandem Duplication
Algo σ → 12 · · · n
Mirror Duplication
Algo 12 · · · n → σ
Step 2 – We construct the path
8 8
7 7
⇓ 6 6
5 5
136 000 4 4
2 001 3 3
2 2
57 011 1 1
4 010 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8
12345678 13468752
8 110
8
7
6
5
4
3
2
1
1 2 3 4 5 6 7 8
Jean-Luc Baril WM Duplication Random Loss Model

58. Model
Introduction
Theorems
Tandem Duplication
Algo σ → 12 · · · n
Mirror Duplication
Algo 12 · · · n → σ
Step 2 – We construct the path
8 8
7 7
⇓ 6 6
5 5
136 000 4 4
2 001 3 3
2 2
57 011 1 1
4 010 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8
12345678 13468752
8 110
8
7
6
5
4
3
2
1
1 2 3 4 5 6 7 8
Jean-Luc Baril WM Duplication Random Loss Model

59. Model
Introduction
Theorems
Tandem Duplication
Algo σ → 12 · · · n
Mirror Duplication
Algo 12 · · · n → σ
Step 2 – We construct the path
8 8
7 7
⇓ 6 6
5 5
136 000 4 4
2 001 3 3
2 2
57 011 1 1
4 010 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8
12345678 13468752
8 110
8
7
6
5
4
3
2
1
1 2 3 4 5 6 7 8
Jean-Luc Baril WM Duplication Random Loss Model

60. Model
Introduction
Theorems
Tandem Duplication
Algo σ → 12 · · · n
Mirror Duplication
Algo 12 · · · n → σ
Step 2 – We construct the path
8 8
7 7
6 6
5 5
136 000 4 4
2 001 3 3
2 2
57 011 1 1
4 010 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8
12345678 13468752
8 110
8
7
6
5
4
3
2
1
1 2 3 4 5 6 7 8
13625784
Jean-Luc Baril WM Duplication Random Loss Model

61. Model
Introduction
Theorems
Tandem Duplication
Algo σ → 12 · · · n
Mirror Duplication
Algo 12 · · · n → σ
Step 2 – We construct the path
8 8
7 7
⇓ 6 6
5 5
136 000 4 4
2 001 3 3
2 2
57 011 1 1
4 010 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8
12345678 13468752
8 110
8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8
13625784
Jean-Luc Baril WM Duplication Random Loss Model

62. Model
Introduction
Theorems
Tandem Duplication
Algo σ → 12 · · · n
Mirror Duplication
Algo 12 · · · n → σ
Step 2 – We construct the path
8 8
7 7
⇓ 6 6
5 5
136 000 4 4
2 001 3 3
2 2
57 011 1 1
4 010 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8
12345678 13468752
8 110
8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8
13625784
Jean-Luc Baril WM Duplication Random Loss Model

63. Model
Introduction
Theorems
Tandem Duplication
Algo σ → 12 · · · n
Mirror Duplication
Algo 12 · · · n → σ
Step 2 – We construct the path
8 8
7 7
⇓ 6 6
5 5
136 000 4 4
2 001 3 3
2 2
57 011 1 1
4 010 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8
12345678 13468752
8 110
8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8
13625784
Jean-Luc Baril WM Duplication Random Loss Model

64. Model
Introduction
Theorems
Tandem Duplication
Algo σ → 12 · · · n
Mirror Duplication
Algo 12 · · · n → σ
Step 2 – We construct the path
8 8
7 7
6 6
5 5
136 000 4 4
2 001 3 3
2 2
57 011 1 1
4 010 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8
12345678 13468752
8 110
8 8
7 7
6 6
5 5
4 4
3 3
2 2
1 1
1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8
13625784 13625748
Jean-Luc Baril WM Duplication Random Loss Model

65. Model
Introduction
Theorems
Tandem Duplication
Algo σ → 12 · · · n
Mirror Duplication
Algo 12 · · · n → σ
Complexity
One step requires : O(n)
Whole process : O(n · log val(σ)) < O(n · log n)
Jean-Luc Baril WM Duplication Random Loss Model