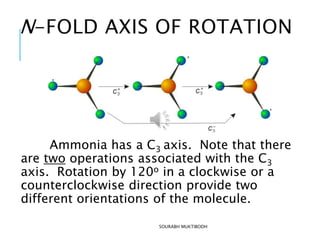
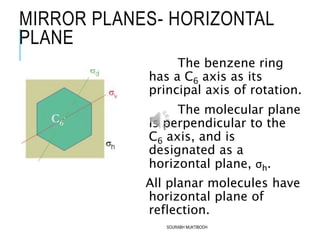
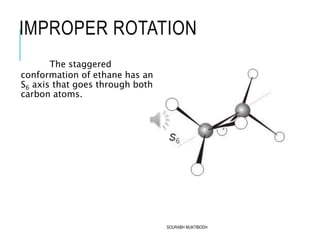
The document discusses symmetry elements and operations in molecular chemistry, highlighting their significance in predicting vibrational spectra, hybridization, and optical activity. It defines and categorizes different types of symmetry elements, including identity, proper rotation, mirror symmetry, and improper rotation, while providing examples and graphical representations. The summary concludes that understanding these symmetry elements allows for the identification of molecular point groups, facilitating the application of group theory in chemistry.

1. SYMMETRY ELEMENTS
AND OPERATIONS
PROF. SOURABH MUKTIBODH
OLD GDC, INDORE
The symmetry
properties of molecules
can be used to predict
vibrational spectra,
hybridization, optical
activity, simplifying
calculations in quantum
mechanics etc.
SOURABH MUKTIBODH

2. THE TERM SYMMETRY IS
ASSOCIATED WITH-
1. Beauty
2. Regularity
3. Periodicity
4. Harmonicity and
5. Systemization
In geometrical objects.
(molecules for chemist)
SOURABH MUKTIBODH

3. GEOMETRICAL OBJECTS
SOURABH MUKTIBODH

4. AND THE MONUMENTS
SOURABH MUKTIBODH

5. THE EIFFIL TOWER
SOURABH MUKTIBODH

6. BEAUTIFUL COLLOIDAL
NANO-PARTICES -
LOOK HOW BEAUTIFUL THEY
ARE…….
SOURABH MUKTIBODH

7. THE QUESTION IS-
How to quantify this beauty aspect
?
and
The answer is……….
SOURABH MUKTIBODH

8. SYMMETRY ELEMENTS AND
OPERATIONS
Symmetry elements are geometrical entities such
as a plane, an axis (of rotation), centers (of inversion),
etc., through which a symmetry operation can be
performed.
A molecule has a given symmetry element if the
operation leaves the molecule looks as if nothing has
changed (even though atoms and bonds may have been
moved). A symmetry operation produces a
superimposable configuration. (equivalent or
identical configuration.)
SOURABH MUKTIBODH

9. SYMMETRY ELEMENTS
Element Symmetry Operation Symbol
Identity E
n-fold axis Rotation by 2π/n Cn
Mirror plane Reflection σ
Center of in- Inversion i
version
n-fold axis of Rotation by 2π/n
Sn
improper rotation followed by reflection
perpendicular to the
axis of rotation

10. IDENTITY, E
All molecules have Identity. This operation leaves
the entire molecule unchanged. A highly asymmetric
molecule such as a tetrahedral carbon with 4 different
groups attached has only identity, and no other
symmetry elements. It also signifies operation
of doing nothing. It is there for
mathematical reasons., such as in Group
theory.
Note- some chemists do not consider
this as an operation.
SOURABH MUKTIBODH

11. N-FOLD AXIS OF ROTATION
Ammonia has a C3 axis. Note that there
are two operations associated with the C3
axis. Rotation by 120o in a clockwise or a
counterclockwise direction provide two
different orientations of the molecule.
SOURABH MUKTIBODH

12. LET US ROTATE BENZENE MOLECULE BY 60 DEGREE,
PERPENDICULAR TO THE MOLECULAR PLANE
C6
1 = C6
1
C6
2 = C3
1
C6
3 = C2
1
C6
4 = C3
2
C6
5 = C6
5
C6
6 = E
Thus a C6 axis generates only two genuine C6
operations. Others can be seen as lower order
operations. A C6 thus generates-
2 C6 ,2 C3 , 1C2
1
2
6
3
5
4
6
1
5
2
4
3
5
6
4
1
3
2
4
5
3
6
2
1
3
4
2
5
1
6
2
3
1
4
5
SOURABH MUKTIBODH

13. A MOLECULE MAY CONTAIN SEVERAL AXES (
HIGHEST ORDER AXIS IS KNOWN AS PRINCIPAL
AXIS), SAY FOR EXAMPLE IN BORON TRIFLUORIDE
MOLECULE-
C3
1 , C3
2 ,3 C2
B F
2
F
1
F
3 SOURABH MUKTIBODH

14. FIND THE HIGHEST ORDER AXIS IN
THE FOLLOWING MOLECULES-
Choloromethane ferrocynide ion
H
ClH
Cl
SOURABH MUKTIBODH

15. Cl
B Cl
Cl
Cl
O
O
O
O
O
O
biphenyl
18-crown-6
SOURABH MUKTIBODH

16. MIRROR PLANES/ SYMMETRY
The reflection of the water
molecule in either of its two mirror
planes results in a molecule that
looks unchanged. A plane of
reflection bisects the molecule
into equal halves. This operation
is denoted by σ .
SOURABH MUKTIBODH

17. REFLECTING TWICE BY THE
SAME PLANE OF COURSE GIVES
ORIGINAL CONFIGURATION -
Plane of symmetry or mirror plane does not generate
number of symmetry operations. As it is obvious that-
1 = 
2 = E
3 = 
4 = E
Thus
n =  if n= odd and n = E if n = even
SOURABH MUKTIBODH

18. TYPES OF MIRROR PLANES-
THEY HAVE BEEN CLASSIFIED
AS OF THREE TYPES-
1. vertical plane of reflection- denoted by v
2. Horizontal plane of of reflection - denoted by h
3. Dihedral plane of reflection - denoted by d
SOURABH MUKTIBODH

19. MIRROR PLANES / SYMMETRY
The subscript “v” in
σv, indicates a vertical
plane of symmetry. This
indicates that the mirror
plane includes the
principal axis of rotation
(C2).
SOURABH MUKTIBODH

20. MIRROR PLANES- HORIZONTAL
PLANE
The benzene ring
has a C6 axis as its
principal axis of rotation.
The molecular plane
is perpendicular to the
C6 axis, and is
designated as a
horizontal plane, σh.
All planar molecules have
horizontal plane of
reflection.
C6
.
SOURABH MUKTIBODH

21. MIRROR PLANES- DIHEDRAL
PLANE The vertical planes,
σv, go through the
carbon atoms, and
include the C6 axis.
The planes that
bisect the bonds are
called dihedral planes,
σd.
A dihedral plane passes
between two mutually
perpendicular C2
C6
.
SOURABH MUKTIBODH

22. XENON TETRAFLUORIDE
MOLECULE CONTAINS ALL
THREE TYPES OF PLANES-
Xe
F F
F F
Xe
F F
F F
Xe
F F
F F
SOURABH MUKTIBODH

23. CENTRE OF INVERSION/ CENTER
OF SYMMETRY
The inversion operation projects each atom through the
center of inversion, and across to the other side of the molecule.
This operation is symbolized by i .
SOURABH MUKTIBODH

24. INVERSION CENTRE
We proceed to identify centre of symmetry as following-
1. choose a centre within the molecule.
2. draw lines in the direction where the atoms are
located.
3. if the same atom in equal and opposite direction is
seen, true for every situation, than the molecule
possesses a centre of symmetry.
SOURABH MUKTIBODH

25. IDENTIFY THE MOLECULES
WHICH CONTAIN POINT OF
INVERSION
H
ClH
Cl
B Cl
Cl
Cl
Cl
ClCl
SOURABH MUKTIBODH

26. IMPROPER ROTATION
An improper rotation is rotation, followed by reflection in the
plane perpendicular to the axis of rotation. Thus
Sn = Cn * i = i * Cn
both independent symmetry operations commute. Essentially
Cn  
SOURABH MUKTIBODH

27. IMPROPER ROTATION
The staggered
conformation of ethane has an
S6 axis that goes through both
carbon atoms.
SOURABH MUKTIBODH

28. IMPROPER ROTATION
Note that an S1 axis
doesn’t exist; it is same as a
mirror plane.
S1 = C1
1 * 1 = E * 1 = 
SOURABH MUKTIBODH

29. NOTE THAT SIMILAR TO PROPER
ROTATION, IMPROPER ROTATION
ALSO GENERATES N-1
OPERATIONS, N BEING THE
ORDER OF AXIS-S4
1 = C4
1 *  1 = S4
1
S4
2 = C4
2 *  2 = C2 * E = C2
1
S4
3 = C4
3 *  3 = S4
3
S4
4 = C4
4 *  4 = E * E = E
Out of four such combinations, only two are true S4
representations. Thus a S4 axis generates only two
genuine symmetry operations.
SOURABH MUKTIBODH

30. IMPROPER ROTATION
Likewise, an S2 axis is a
center of inversion.
S 2= i
SOURABH MUKTIBODH

31. EX. IDENTIFY ALL SYMMETRY
ELEMENTS AND OPERATIONS OF
THE FOLLOWING MOLECULES-
O
HH N H
H
H
E
C2
v
v`
E
C3
3v
SOURABH MUKTIBODH

32. SIMILARLY IDENTIFY ALL
ELEMENTS AND OPERATIONS
FOR SYMMETRIC BF3 MOLECULE
E
C3
1 and C3
2
C2 (Along B—F1 bond)
C2 (Along B—F2 bond)
C2 (Along B—F3 bond)
v (Along B—F1 bond)
v ` (Along B—F2 bond)
v’ (Along B—F3 bond)
h ( molecular plane)
S3
1 and S3
2
B F
2
F
1
F
3
SOURABH MUKTIBODH

33. SUMMARY
1. Symmetry elements and operations are though, two
slightly different terms, but are often treated collectively.
2. A symmetry operation produces superimposable
configuration.
3. There are five fundamental symmetry elements and
operations. They are 1. identity (E) 2. proper rotation (
Cn) 3. mirror symmetry or reflection () 4. centre of
symmetry or inversion centre (i) and 5. improper
rotation.(Sn)
4. A molecule may or may not contain all symmetry
elements and operations. More operations present
assures more symmetric nature.
5. Symmetry elements and operations allow us to identify
point group of the molecule and then detailed
applications of group theory can be explored.
SOURABH MUKTIBODH

34. REFERENCES
A.F.Cotton “ Chemical Applications of Group Theory”
ISBN 0471510947
Next- Molecular point group
SOURABH MUKTIBODH