Downloaded 388 times
Uploaded byRichard Ore Cayetano
05 groundwater flow equations
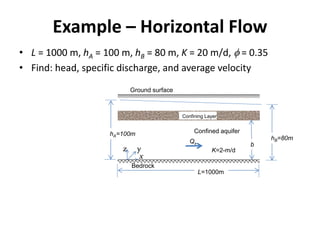
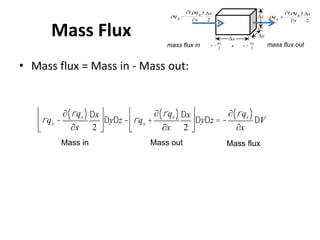
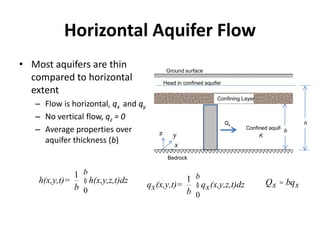
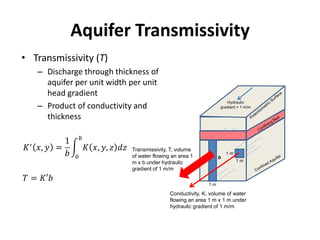
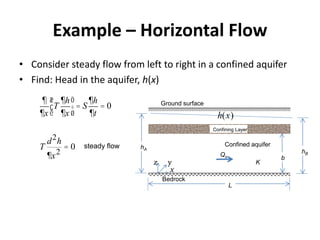
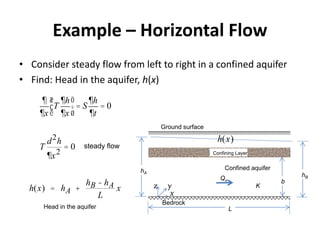
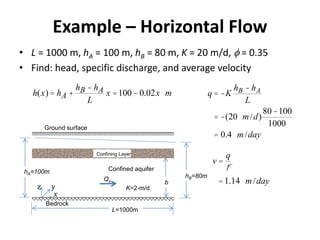
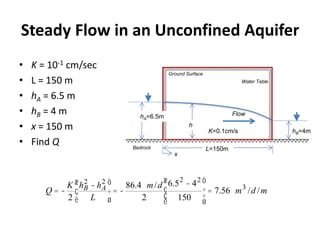
- The document discusses equations for analyzing groundwater flow in confined and unconfined aquifers. - For confined aquifers, the continuity equation is integrated over the aquifer thickness to derive an equation using transmissivity. Examples are presented of steady horizontal and radial flow. - For unconfined aquifers, Dupuit assumptions are used and the continuity equation is solved for steady 1D flow using the water table elevation. Worked examples are provided for both confined and unconfined cases.
More Related Content
Similar to 05 groundwater flow equations
05 groundwater flow equations
- 1. Groundwater Flow Equations GroundwaterHydraulics Daene C. McKinney
- 2. Summary • General GroundwaterFlow – Control Volume Analysis – General Continuity Equation • Confined Aquifer Flow – Continuity Equation – Integrate over vertical dimension – Transmissivity – Continuity – Examples • Unconfined Aquifer Flow – Darcy Law – Continuity Equation – Examples
- 3. Control Volume • Controlvolume of dimensions Dx, Dy, Dz • Completely saturated with a fluid of density r x yz Mass flux in Mass flux out 2 x x D 2 x x D 2 )( x x q q x x D r r 2 )( x x q q x x D r r xD x yD zD Control volume
- 4. Mass Flux • Massflux = Mass in - Mass out: mass flux in mass flux out2 x x D 2 x x D 2 )( x x q q x x D r r 2 )( x x q q x x D r r xD x yD zD rqx - ¶ rqx( ) ¶x Dx 2 é ë ê ù û úDyDz - rqx + ¶ rqx( ) ¶x Dx 2 é ë ê ù û úDyDz = - ¶ rqx( ) ¶x DV Mass fluxMass in Mass out
- 5. Mass Flux • Massflux = • Continuity: Mass flux = change of mass • Fluid mass in the volume: • Continuity mass flux in mass flux out2 x x D 2 x x D 2 )( x x q q x x D r r 2 )( x x q q x x D r r xD x yD zD - ¶ rqx( ) ¶x DV m =frDV Mass flux change of mass
- 6. Aquifer Storage Water compressibilityAquifer compressibility Chain rule Now, put it back into the continuity equation
- 7.
- 8.
- 9. Horizontal Aquifer Flow •Most aquifers are thin compared to horizontal extent – Flow is horizontal, qx and qy – No vertical flow, qz = 0 – Average properties over aquifer thickness (b) h(x,y,t)= 1 b h(x,y,z,t)dz 0 b ò Ground surface Bedrock Confined aquifer Qx K x yz h Head in confined aquifer Confining Layer b qx(x,y,t)= 1 b qx(x,y,z,t)dz 0 b ò Qx = bqx
- 10. Aquifer Transmissivity • Transmissivity(T) – Discharge through thickness of aquifer per unit width per unit head gradient – Product of conductivity and thickness Hydraulic gradient = 1 m/m b 1 m 1 m 1 m Transmissivity, T, volume of water flowing an area 1 m x b under hydraulic gradient of 1 m/m Conductivity, K, volume of water flowing an area 1 m x 1 m under hydraulic gradient of 1 m/m
- 11. Continuity Equation • Continuityequation • Darcy’s Law • Continuity - ¶Qx ¶x = S ¶h ¶t Qx = -Tx ¶h ¶x ¶ ¶x Tx ¶h ¶x æ è ç ö ø ÷ = S ¶h ¶t Ground surface Bedrock Confined aquifer Qx K x yz h Head in confined aquifer Confining Layer b 1 r ¶ ¶r r ¶h ¶r æ è ç ö ø ÷ = S T ¶h ¶t Radial Coordinates
- 12. Example – HorizontalFlow • Consider steady flow from left to right in a confined aquifer • Find: Head in the aquifer, h(x) ¶ ¶x T ¶h ¶x æ è ç ö ø ÷ = S ¶h ¶t = 0 T d2 h ¶x2 = 0 Ground surface Bedrock Confined aquifer Qx K x yz hB Confining Layer b hA L steady flow h(x)
- 13. Example – HorizontalFlow • L = 1000 m, hA = 100 m, hB = 80 m, K = 20 m/d, f = 0.35 • Find: head, specific discharge, and average velocity Ground surface Bedrock Confined aquifer Qx K=2-m/d x yz hB=80m Confining Layer b hA=100m L=1000m
- 14.
- 15. Flow in anUnconfined Aquifer • Dupuit approximations – Slope of the water table is small – Velocities are horizontal Ground surface Bedrock Unconfined aquifer Water table Dx Qx K h x yz Qx = qxh = (-K ¶h ¶x )h - ¶Qx ¶x = Sy ¶h ¶t ¶ ¶x Kh ¶h ¶x æ è ç ö ø ÷ = Sy ¶h ¶t
- 16. Steady Flow inan Unconfined Aquifer • 1-D flow • Steady State, • K = constant • Find h(x) ¶ ¶x Kh ¶h ¶x æ è ç ö ø ÷ = Sy ¶h ¶t h FlowhA hB Water Table Ground Surface Bedrock L x
- 17. Steady Flow inan Unconfined Aquifer • K = 10-1 cm/sec • L = 150 m • hA = 6.5 m • hB = 4 m • x = 150 m • Find h(x), Q h FlowhA=6.5m hB=4m Water Table Ground Surface Bedrock L=150m x K=0.1cm/s
- 18. Summary • General GroundwaterFlow – Control Volume Analysis – General Continuity Equation • Confined Aquifer Flow – Continuity Equation – Integrate over vertical dimension – Transmissivity – Continuity – Examples • Unconfined Aquifer Flow – Darcy Law – Continuity Equation – Examples
- 19.
- 20. Example – HorizontalFlow • Consider steady flow from left to right in a confined aquifer • Find: Head in the aquifer, h(x) ¶ ¶x T ¶h ¶x æ è ç ö ø ÷ = S ¶h ¶t = 0 T d2 h ¶x2 = 0 h(x) = hA + hB - hA L x Ground surface Bedrock Confined aquifer Qx K x yz hB Confining Layer b hA L steady flow Head in the aquifer h(x)
- 21. Example – HorizontalFlow • L = 1000 m, hA = 100 m, hB = 80 m, K = 20 m/d, f = 0.35 • Find: head, specific discharge, and average velocity h(x) = hA + hB - hA L x =100- 0.02x m q = -K hB - hA L = -(20 m/d) 80 -100 1000 = 0.4 m/day v = q f =1.14 m/day Ground surface Bedrock Confined aquifer Qx K=2-m/d x yz hB=80m Confining Layer b hA=100m L=1000m
- 22. Steady Flow inan Unconfined Aquifer • 1-D flow • Steady State, • K = constant ¶ ¶x Kh ¶h ¶x æ è ç ö ø ÷ = Sy ¶h ¶t d dx Kh dh dx æ è ç ö ø ÷ = 0 h2 (x) = hA 2 +( hB 2 - hA 2 L )x h FlowhA hB Water Table Ground Surface Bedrock L x Q = (-K dh dx )h = - K 2 dh2 dx = - K 2 hB 2 - hA 2 L æ è ç ö ø ÷
- 23. Steady Flow inan Unconfined Aquifer • K = 10-1 cm/sec • L = 150 m • hA = 6.5 m • hB = 4 m • x = 150 m • Find Q h FlowhA=6.5m hB=4m Water Table Ground Surface Bedrock L=150m x Q = - K 2 hB 2 - hA 2 L æ è ç ö ø ÷ = - 86.4 m/d 2 6.52 - 42 150 æ è ç ç ö ø ÷ ÷ = 7.56 m3 /d /m K=0.1cm/s