The Universal Bayesian Chow-Liu Algorithm summarizes a document describing a method for learning Bayesian networks from data that can contain both discrete and continuous variables. It constructs a tree structure that maximizes the posterior probability based on estimating mutual information between all variable pairs. The algorithm was tested on real world medical data containing different variable types. Future work includes developing an R command to implement the full algorithm.

1. The Universal Bayesian Chow-Liu Algorithm
Joe
Osaka University
October 27, 2013
DDS 2013
Keio University (Hiyoshi)

2. Road Map
Chow-Liu Algorithm via MDL
Without assuming either discrete or continuous
Experiments
Concluding Remarks

3. Chow-Liu, 1968 (Tree Approximation)
X(1), · · · , X(N): N (≥ 1) discrete random variables
V := {1, · · · , N} and E ⊆ {{i, j}|i = j, i, j ∈ V } consist of a tree:
Approximate P1,··· ,N(x(1), · · · , x(N)) by
Q(x(1)
, · · · , x(N)
|E) =
{i,j}∈E
Pi,j (x(i), x(j))
Pi (x(i))Pj (x(j)) i∈V
Pi (x(i)
)
I(i, j): Mutual Information between X(i), X(j)
Kullback-Leibler D(P1,··· ,N||Q) → min
Unless making a loop, connect {i, j} maximizing I(i, j) as an edge

4. Example
i 1 1 2 1 2 3
j 2 3 3 4 4 4
I(i, j) 12 10 8 6 4 2
❥ ❥
❥ ❥
2 4
1 3
❥ ❥
❥ ❥
2 4
1 3
❥ ❥
❥ ❥
2 4
1 3
❥ ❥
❥ ❥
2 4
1 3
❅❅

5. Why Chow-Liu works?
D(P1,··· ,N||Q) = −H(1, · · · , N) +
N
i∈V
H(i) −
{i,j}∈E
I(i, j)
Kruskal’s Algorithm:
◮ Unless making a loop, connects e ∈ E maximizing w(e)
◮ constructs a tree (V , E) maximizing
e∈E
w(e)
w : E → R≥0

6. Chow-Liu: Tree Learning via Maximum Likelihood
Learning rather than Approximation
Starting from n examples xn = {(x
(j)
i )N
j=1}n
i=1 rather than P1,··· ,N
Calculate relative frequencies ˆpi , ˆpi,j given xn to obtain
ˆHn
(xn
|E) := n
i∈V
ˆH(i) − n
{i,j}∈E
ˆI(i, j)
Empirical entropy ˆHn
(xn
|E) → min
Unless making a loop, connect {i, j} maximizing ˆI(i, j) as an edge

7. Chow-Liu: Tree Learning via MDL (Suzuki, 1993)
π(E): Prior Probability of E assuming to be uniform
Description Length of xn under E:
L(xn
|E) := ˆHn
(xn
|E) +
1
2
k(E) log n
# of Parameters:
k(E) :=
i∈V
α(i)
+
{i,j}∈E
(α(i)
− 1)(α(j)
− 1)
α(i): the # of values X(i) takes
Description Length L(xn
|E) − log π(E) → min
Unless making a loop, connect {i, j} maximizing ˆJ(i, j) as an edge
ˆJ(i, j) = ˆI(i, j) −
1
2n
(α(i)
− 1)(α(j)
− 1) log n

8. ML vs MDL
ML MDL
Choice ˆHn(xn|E) ˆHn(xn|E) + 1
2k(E) log n
of E → min → max
Choice ˆI(i, j) ˆI(i, j)
of {i, j} → max − 1
2n (α(i) − 1)(α(j) − 1) log n
→ max
Criteria Fitness of xn to E Fitness of xn to E
Simplicity of E
Target Trees Forests
Correctness Overestimation Correct as n grows
ML seeks a tree even if the random variables are independent.

9. Chow-Liu: Tree Learning via Bayes (Suzuki, 2012)
Replace {Pi (x(i))}i∈V and {Pi,j (x(i), x(j))}{i,j}∈E in
Q1,··· ,N(x(1)
, · · · , x(N)
|E) =
{i,j}∈E
Pi,j(x(i), x(j))
Pi (x(i))Pj (x(j)) i∈V
Pi (x(i)
)
by {R(i)}i∈V and {R(i, j)}{i,j}∈E in
Rn
(xn
|E) :=
{i,j}∈E
Rn(i, j)
Rn(i)Rn(j)
i∈V
Rn
(i)
Posterior Probability π(E)Rn
(xn
|E) → max
Unless making a loop, connect {i, j} maximizing J(i, j) as an edge
J(i, j) :=
1
n
log
Rn(i, j)
Rn(i)Rn(j)

10. MDL reduces to Bayes
If we choose {R(i)} and {R(i, j)} properly,
L(xn
|E) = − log Rn
(xn
|E) ⇐⇒ Rn
(xn
|E) = 2−L(xn|E)
ˆJ(i, j) = J(i, j)
Universality: require Rn
(·|·) to satisfy
1
n
log
Qn(xn|E)
Rn(xn|E)
→ 0 as n → ∞
for any Qn(·|·).

11. zip, gzip, uuencode, lzh, etc
A: finite set
ϕ : An → {0, 1}∗ (Data Compression)
l(xn): the output length of xn ∈ An w.r.t. ϕ
Rn(xn) := 2−l(xn) satisfies
1
n
log
Pn(xn)
Rn(xn)
→ 0 as n → ∞
for any Probability Pn(xn) of xn ∈ An

12. Without assuming {X(i)
}N
i=1 to be discrete
In any database some fields are discrete others continuos:
◮ discrete (finite/infinite)
◮ continuous
◮ others (neither discrete or continuous)
Neither discrete or continuous (Suzuki, 2011)
constructed generalized universal density function gn(xn)
1
n
log
f n(xn)
gn(xn)
→ 0 as n → ∞
for any generalized probability density function f n(xn)

13. Example
{Aj }: Aj+1 is a refinement of Aj .
A1 = {[0, 1/2), [1/2, 1)}
A2 = {[0, 1/4), [1/4, 1/2), [1/2, 3/4), [3/4, 1)}
. . .
Aj = {[0, 2−(j−1)), [2−(j−1), 2 · 2−(j−1)), · · · , [(2j−1 − 1)2−(j−1), 1)}
. . .
sj : A → Aj (quantization, x ∈ a ∈ Aj =⇒ sj (x) = a)
λ: Lebesgue measure (width)
Qn
j : universal measure w.r.t. Aj
(sj (x1), · · · , sj (xn)) = (a1, · · · , an) =⇒ gn
j (xn
) :=
Qn
j (a1, · · · , an)
λ(a1) · · · λ(an)
{ωj }: ωj > 0, j ωj = 1
gn
(xn
) =
j
ωjgn
j (xn
)

14. Bayesian Estimator of Mutual Information
J(i, j) :=
1
n
log
Rn(i, j)
Rn(i)Rn(j)
X(i), X(j) may be any pair of discrete, or continuous, or others
Previous Work
Liang, 2004 only deals with discrete variables (after Suzuki, 1993)
Edwords, et.al 2010 assumes that the discrete and continuous
variables are connected.

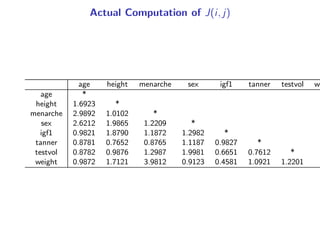
15. Experiments using R
juul2 data frame in the ISwR package contains insulin-like growth
factor, one observation per subject in various ages, with the bulk of
the data collected in conection with physical examinations.
n = 1336
setClass("random.variable", representation(data="numeric",
breaks="array",width="array"))
setClass("continuous", contains="random.variable",
representation(mu="numeric",sigma="numeric"))
setClass("discrete", contains="random.variable")
X[[1]]<-new("continuous", data=juul2$age)
X[[2]]<-new("continuous", data=juul2$height)
X[[3]]<-new("discrete", data=juul2$menarche)
X[[4]]<-new("discrete", data=juul2$sex)
X[[5]]<-new("discrete", data=juul2$igf1)
X[[6]]<-new("discrete", data=juul2$tanner)
X[[7]]<-new("discrete", data=juul2$testvol)
X[[8]]<-new("continuous", data=juul2$weight)

16. Actual Computation of J(i, j)
age height menarche sex igf1 tanner testvol we
age *
height 1.6923 *
menarche 2.9892 1.0102 *
sex 2.6212 1.9865 1.2209 *
igf1 0.9821 1.8790 1.1872 1.2982 *
tanner 0.8781 0.7652 0.8765 1.1187 0.9827 *
testvol 0.8782 0.9876 1.2987 1.9981 0.6651 0.7612 *
weight 0.9872 1.7121 3.9812 0.9123 0.4581 1.0921 1.2201

17. Concluding Remarks
n: sample size
N: # of variables
L: the maximum depth of quantizations
Computation
O(n), O(N2), and O(L)
Bayesian Chow-Liu Algorithm
In any database, some fields are discrete and others are continuous.
◮ Easy programming
◮ Fast Computation
Future Work: constructing a R command
Currently, specify either discrete or continuous for each variable.