Downloaded 23 times
Uploaded byNir Soffer
Game theory and strategy (PCA16, PCATX)
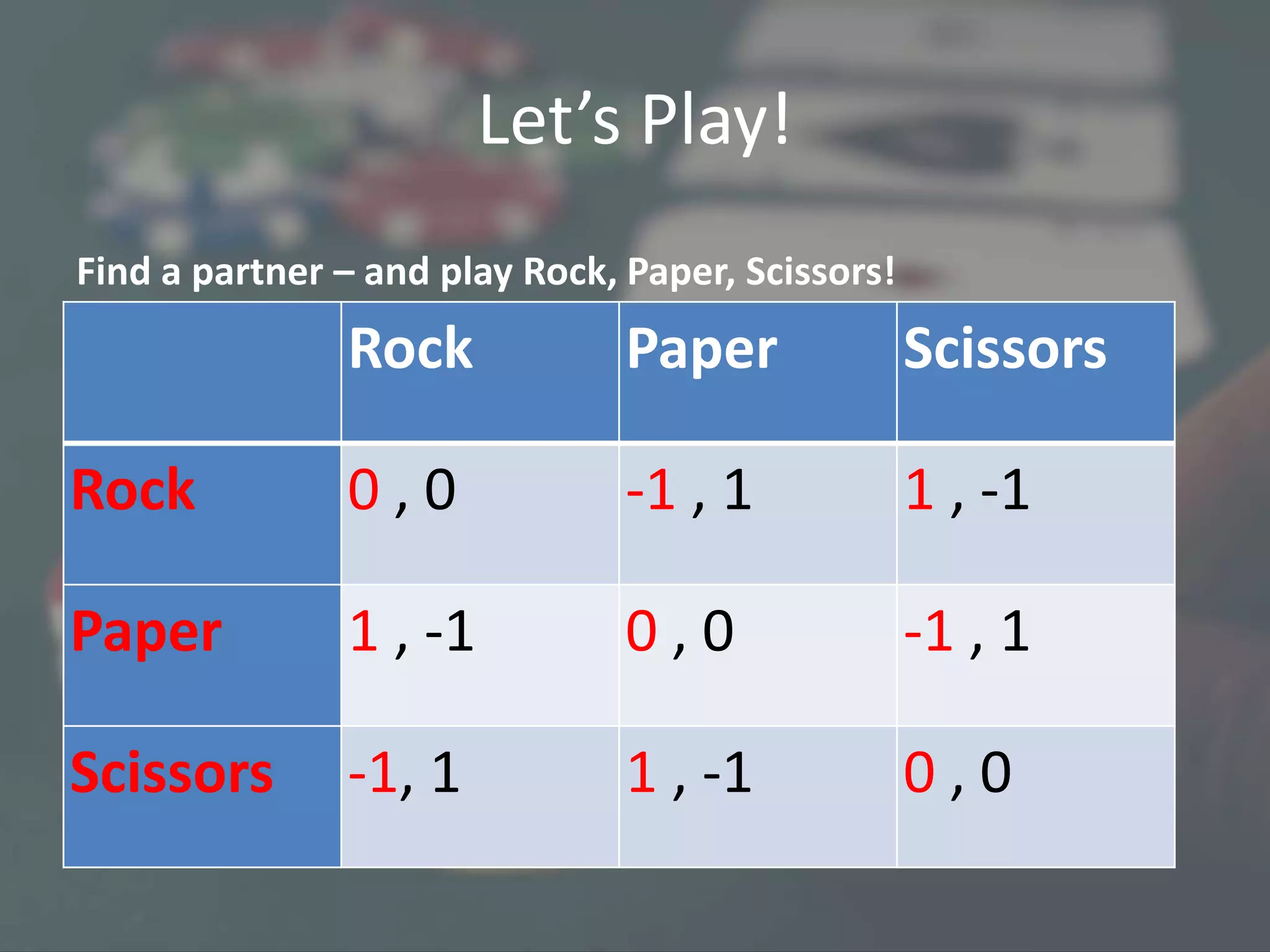
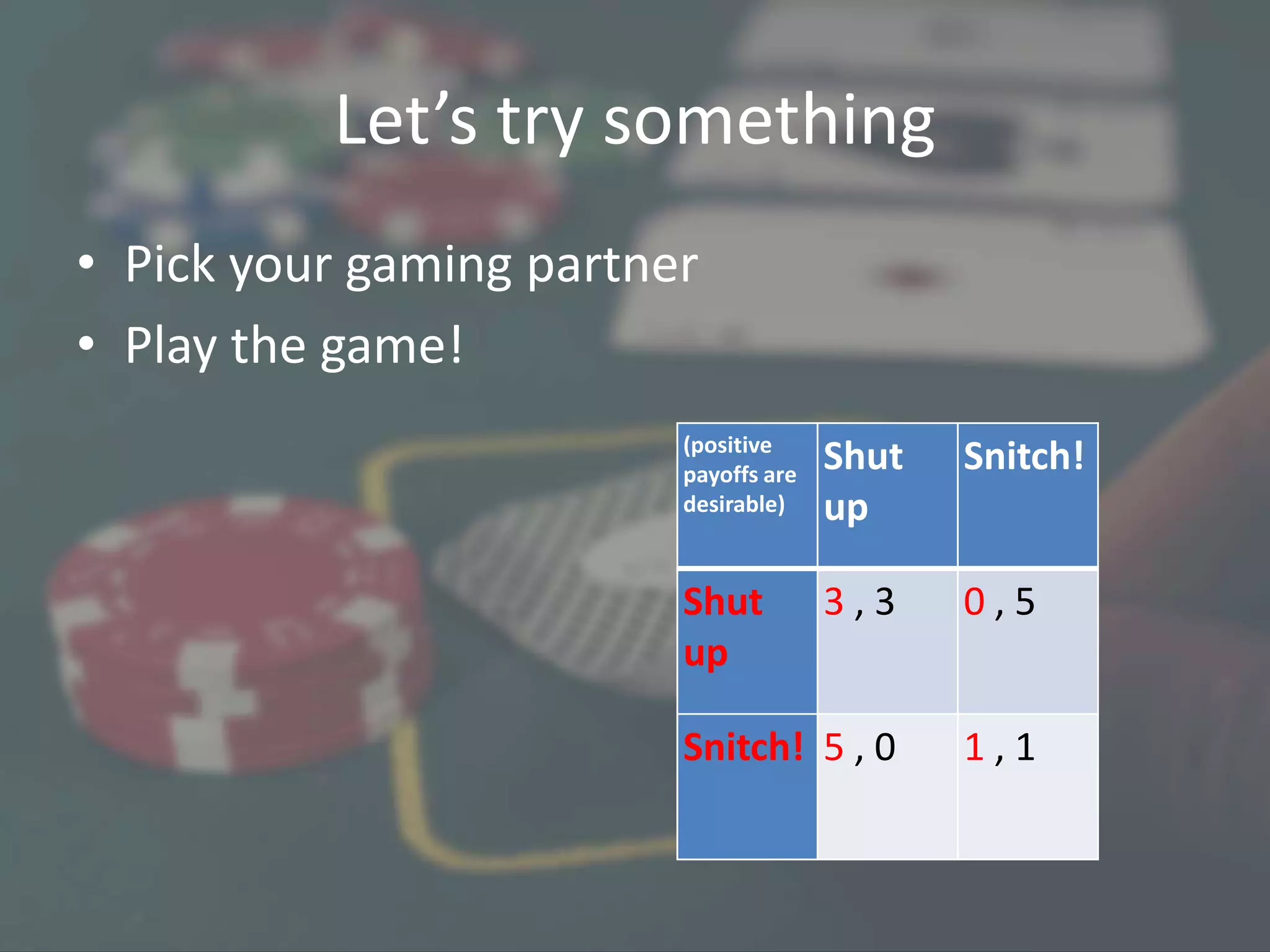
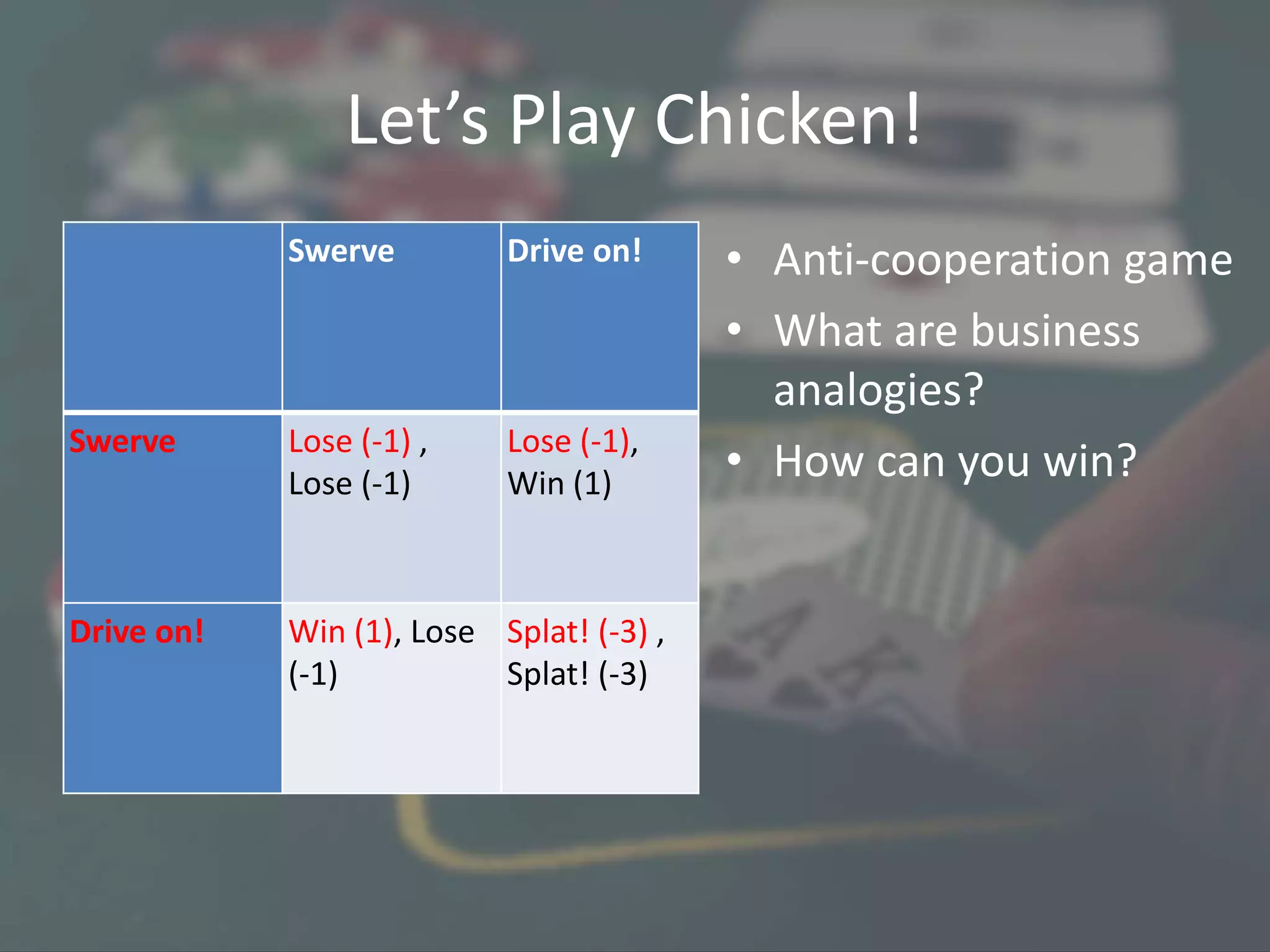
The document provides a primer on game theory, discussing its concepts and applicability to product strategy and competitive behavior. It covers various games like rock-paper-scissors and the prisoner’s dilemma, explaining their relevance to business scenarios such as pricing strategies and market competition. The document also emphasizes the importance of understanding cooperative behavior in competitive situations to optimize outcomes.
More Related Content
Similar to Game theory and strategy (PCA16, PCATX)
Game theory and strategy (PCA16, PCATX)
- 2.
- 3. What? • A primeron basic game theory concepts – Basic – We try to avoid math – If you know a lot about Game Theory already, you may get bored • A discussion on applying game theoretic concepts to product strategy
- 4. Why? • I thinkGame Theory is Fun! • Interesting and illuminating perspective on behavior of both people and firms • Analytical toolset for competitive scenarios
- 5. Who? • From Israel •Student of Behavior and Business • GTM Consultant for multiple startups • Previously PdM and Strategist in Dell and EMC and a variety of software development roles • Winner of the non existent “crappiest slide in PCA15” award
- 6. Agenda • What isGame Theory? • A Few Games and Business Analogies – Rock, Paper, Scissors: • Zero-sum, symmetric game – Prisoner’s Dilemma: • Pricing, market entry, volume • Iterated Prisoner’s Dilemma: TFT • Collusion/Cooperation in IPD – cartels – Chicken and the Value of Commitments • Investment, market entry
- 7. What is GameTheory? • Mathematical discipline designed to answer questions like: – You are playing Rock Paper Scissors. Which do you choose? – Can some games be “solved”? (Tic Tac Toe, Chess, Go?) – Should we build more nuclear weapons in the cold war or less? How do we ensure that a disarmament agreement is enforceable? • Developed mathematically by Von Neumann (of the Manhattan Project fame), Nash (Of “A Beautiful Mind” fame), and Morgenstern (not as famous, but definitely deserves props) during 40s and 50s.
- 8. So, what doesthat have to do with me? • You sell a product that is very similar to your competitor. Do you: – Price low to steal his customers? – Price the same? – Price higher? • You need to invest in a factory to create your product • You open a gas station – should you locate it across the street from your competition or the other side of town? – Who can give an example of something more tech-y that is gas-station-esque?
- 9. Types of Games •Sequential vs. Simultaneous – Sequential: Chess, Checkers, Tic-Tac-Toe • Solvable • Game tree solution – Simultaneous: Rock Paper Scissors • Solvable • Equilibria solutions • Most business problems are simultaneous (or very close to it) rather than sequential • Our focus will be simultaneous, 2 player games
- 10. Brain Teaser –Cut the Cake • Two twin brothers have gotten a cake from their parents for their birthday. • What is the best way for them to split it so they are both happy?
- 11. Rock, Paper, Scissors Thisis a game Rock Paper Scissors Rock 0 , 0 -1 , 1 1 , -1 Paper 1 , -1 0 , 0 -1 , 1 Scissors -1, 1 1 , -1 0 , 0 So how do I read it? • The first number in each pair is the payout for the row player – the second is for the column So, who cares? • This is a boring game – but it’s here as an example for more interesting ones • Still – interesting to note: – Symmetric – Zero Sum
- 12. Rock, Paper, Scissors RockPaper Scissors Rock 0 , 0 -1 , 1 1 , -1 Paper 1 , -1 0 , 0 -1 , 1 Scissors -1, 1 1 , -1 0 , 0 So, again, I ask, who cares? • RPS is a classic example for a zero sum, symmetric game – Zero sum: Winning is done at the expense of the loser – Symmetric: Identical options with identical payoffs exist to all players
- 13. Let’s Play! Find apartner – and play Rock, Paper, Scissors! Rock Paper Scissors Rock 0 , 0 -1 , 1 1 , -1 Paper 1 , -1 0 , 0 -1 , 1 Scissors -1, 1 1 , -1 0 , 0
- 14. What have welearned? • Does RPS have much in common with real business problems? • What’s the best strategy for playing RPS?
- 15. Prisoner’s Dilemma • Aclassic! • Probably most famous game in Game Theory • We are going to spend some time here, so get comfy
- 16. So, what’s thebig deal? (positive payoffs are desirable) Shut up Snitch! Shut up 3 , 3 0 , 5 Snitch! 5 , 0 1 , 1 • Two burglars are busted and put in separate rooms • Police interrogate and promise the first one to snitch a deal • Now, things get interesting. • What would you do?
- 17. Equilibrium (positive payoffs are desirable) Shut up Snitch! Shut up 3 ,3 0 , 5 Snitch! 5 , 0 1 , 1 • The problem should be clear • Everyone would be better off shutting up – but each individual would rather snitch • Therefore, the Nash Equilibrium (and therefore the result of the game if played by rational, payoff maximizing players) is the sub optimal bottom right corner
- 18. What does PDapply to? • Can you think of any real life scenario in which PD applies to?
- 19. A ton ofthem! • Pricing/Promotions: We are selling a similar product; should I price low (and then steal share) or high? – http://www.businessweek.com/articles/2013-11- 19/best-buy-and-the-holiday-retail-prisoners-dilemma • “Feature Wars” • In fact, most non-zero sum games in which cooperation yields more benefits than competing can be modeled like a PD game
- 20. So what dowe do? • The bad news: The solution to a standard, “pure” Prisoner’s Dilemma game is always mutual defection. Sorry. It’s a cruel world. • The good news: Reality is infinitely more complex; there are factors we can explore and ways to “change the game” – IPD – Collusion (don’t do that!) – Change the Game
- 21. Let’s try something •Pick your gaming partner • Play the game! (positive payoffs are desirable) Shut up Snitch! Shut up 3 , 3 0 , 5 Snitch! 5 , 0 1 , 1
- 22. Show of Hands •Who picked snitching? Why? • Who picked shutting up? Why?
- 23. And now, aTwist! • Play the game again. • And again. • And again. • Until I tell you to stop.
- 24. Iterated Prisoner’s Dilemma •An interesting result emerges when playing PD multiple times. Why? • What if I told you that you had exactly 100 turns to play? • Strategies: TFT, TF2TT • Axelrod’s Successful Strategy: – Clear – Provocable – Nice – Forgiving
- 25. Collusion Careful! I’m nota lawyer, but usually, this is illegal Excerpt from Cramton & Schwartz 2002 – see table 1 at http://drum.lib.umd.edu/bitstream/1903/7061/1/cramton-schwartz-collusive-bidding.pdf (can’t put table here for copyright reasons)
- 26. Change the Game •What are other options to change the game? • What if you locked the loot from the burglary with two keys? • Examples from a Product Strategy perspective: – Differentiation – Consortiums (pooled standard ownership for IP) – Punitive clauses in contracts – Price matching clauses (retroactive ones as well) – Most favored customer clauses
- 27. Let’s Play Chicken! SwerveDrive on! Swerve Lose (-1) , Lose (-1) Lose (-1), Win (1) Drive on! Win (1), Lose (-1) Splat! (-3) , Splat! (-3) • Anti-cooperation game • What are business analogies? • How can you win?
- 28. The Factory Game(A version of Chicken) • What’s the Nash equilibrium? • How do you win? Build Not Build Build Competition : 1, 1 Monopoly: 2, 0 Not Build Monopoly: 0, 2 Nothing: 0, 0
- 29. Some interesting questionsif we have time left • You need to bid on ad keywords. Are you better off having keywords that are identical, or different from your competition? • Do you think it’s better to ape your competitors features or remove them entirely? • When you build a store location – would you rather build it next to your competitor, or somewhere else?
- 30. Hotelling’s Problem –or why Differentiation doesn’t always Work The setting – the beach; the adversaries – two hot dog cart vendors. • Where should they place their carts? • What is the socially optimal placement? • What is the actual equilibrium? • Why do I care? Differentiation only matters when it’s difficult or costly to copy
- 31. Do We HaveTime for One More? • This is a game called “Keynesian Beauty Contest” • The story is that of a beauty contest: Given faces published in a newspaper, pick the prettiest face. The winner is the one who picked the most popular face. • We’ll model this here in a variant.
- 32. Pick a card,any card • The options are numbers from 1-10 • The winner is the person who guesses closest to 2/3 of the average • Ready? Go! Either scan the QR code with a QR code scanning up – go to : http://shortn.me/kFiK Or text: GAMES to (952) 649-5350
- 33.
- 34.
- 35.
- 36. Further Reading • Artof Strategy: Dixit & Nalebuff • Evolution of Cooperation: Axelrod • Prisoner’s Dilemma: Poundstone • Coursera: Game Theory, Advanced Game Theory
Editor's Notes
- #4 No Nash equilibrium or minimax theory (unless you really want to); no game trees; no dominant and dominated strategies; no games with imperfect information – just the basics.
- #15 Here’s a hint – not many business problems are zero sum ; there is almost always a way to grow the pie. Assuming perfectly rational players – mixed 1/3 1/3 1/3 strategy is Nash equiblirium
- #20 Yes, has to be symmetric
- #28 Business analogies – (factory next slide) Commitment signaling (option limiting)
- #29 Commitment signaling (Build a larger factory than you have to – means that you can undercut price and try to maintain money) What are some examples that don’t involve physical goods? Website launch in a locale Setting up a large sales office Investing heavily and publicly in a product feature that both companies want Visibility is key for signaling to work