Kerと場合分け

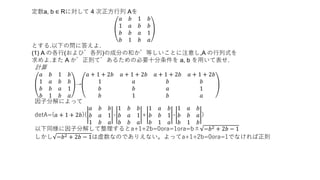
1. 定数a, b ∈ Rに対して 4 次正方行列 Aを
𝑎 𝑏 1 𝑏
1 𝑎 𝑏 𝑏
𝑏 𝑏 𝑎 1
𝑏 1 𝑏 𝑎
とする.以下の問に答えよ.
(1) A の各行(および各列)の成分の和が等しいことに注意し,A の行列式を 求
めよ.また A が正則であるための必要十分条件を a, b を用いて表せ.
(2) TA を A によって定まる R4 の線形変換,つまり,TA(x) = Ax (x ∈ R4) とする.a =
1 のとき,TA の核 Ker (TA) の次元と一組の基底を求めよ.

2. 定数a, b ∈ Rに対して 4 次正方行列 Aを
𝑎 𝑏 1 𝑏
1 𝑎 𝑏 𝑏
𝑏 𝑏 𝑎 1
𝑏 1 𝑏 𝑎
とする.以下の問に答えよ.
(1) A の各行(および各列)の成分の和が等しいことに注意し,A の行列式を
求めよ.また A が正則であるための必要十分条件を a, b を用いて表せ.
計算
𝑎 𝑏 1 𝑏
1 𝑎 𝑏 𝑏
𝑏 𝑏 𝑎 1
𝑏 1 𝑏 𝑎
→
𝑎 + 1 + 2𝑏 𝑎 + 1 + 2𝑏 𝑎 + 1 + 2𝑏 𝑎 + 1 + 2𝑏
1 𝑎 𝑏 𝑏
𝑏 𝑏 𝑎 1
𝑏 1 𝑏 𝑎
因子分解によって
detA=(𝑎 + 1 + 2𝑏)(
𝑎 𝑏 𝑏
𝑏 𝑎 1
1 𝑏 𝑎
-
1 𝑏 𝑏
𝑏 𝑎 1
𝑏 𝑏 𝑎
+
1 𝑎 𝑏
𝑏 𝑏 1
𝑏 1 𝑎
-
1 𝑎 𝑏
𝑏 𝑏 𝑎
𝑏 1 𝑏
)
以下同様に因子分解して整理するとa+1+2b=0ora=1ora=b± −𝑏2 + 2𝑏 − 1
しかし −𝑏2 + 2𝑏 − 1は虚数なのでありえない。よってa+1+2b=0ora=1でなければ正則

3. 定数a, b ∈ Rに対して 4 次正方行列 Aを
𝑎 𝑏 1 𝑏
1 𝑎 𝑏 𝑏
𝑏 𝑏 𝑎 1
𝑏 1 𝑏 𝑎
とする.以下の問に答えよ.
(2) TA を A によって定まる R4 の線形変換,つまり,TA(x) = Ax (x ∈ R4) とす
る.a = 1 のとき,TA の核 Ker (TA) の次元と一組の基底を求めよ.
a=1の時detA=0より1≦rank(kerT) またb=-1の時
A=
1 −1 1 −1
1 1 −1 −1
−1 −1 1 1
−1 1 −1 1
rankA=2 この時t(0110),t(1001)はkerTの基底
a=1でbが−１でない時
1 𝑏 1 𝑏
1 1 𝑏 𝑏
𝑏 𝑏 1 1
𝑏 1 𝑏 1
この時t(1-1-11)がkerTの基底
aが１でない時a+1+2b=0
t(1000)t(0100)t(0010)はTで移しても独立である。
よってrank(kerT)≦1 t(1111)がkerTの基底である。