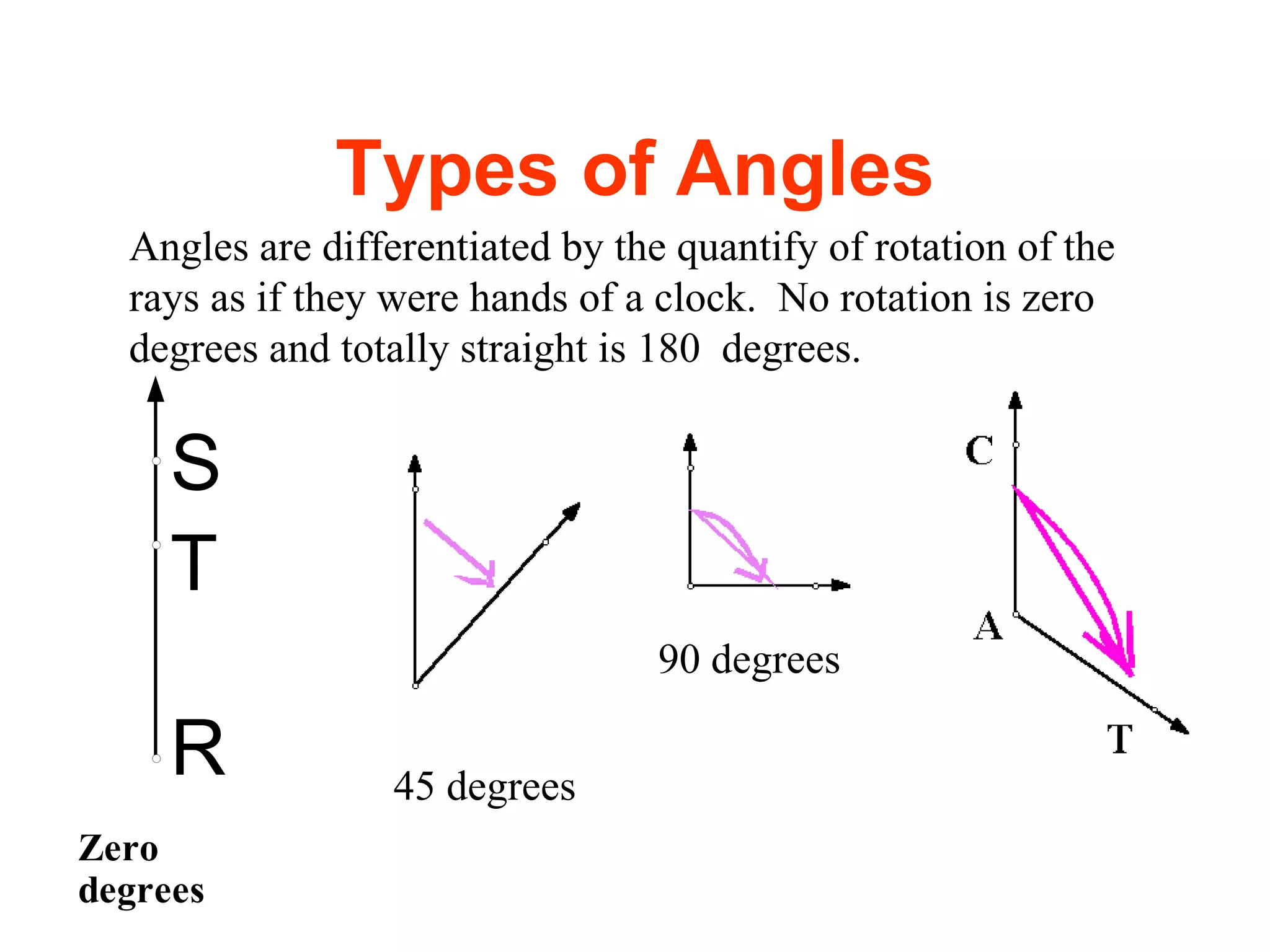
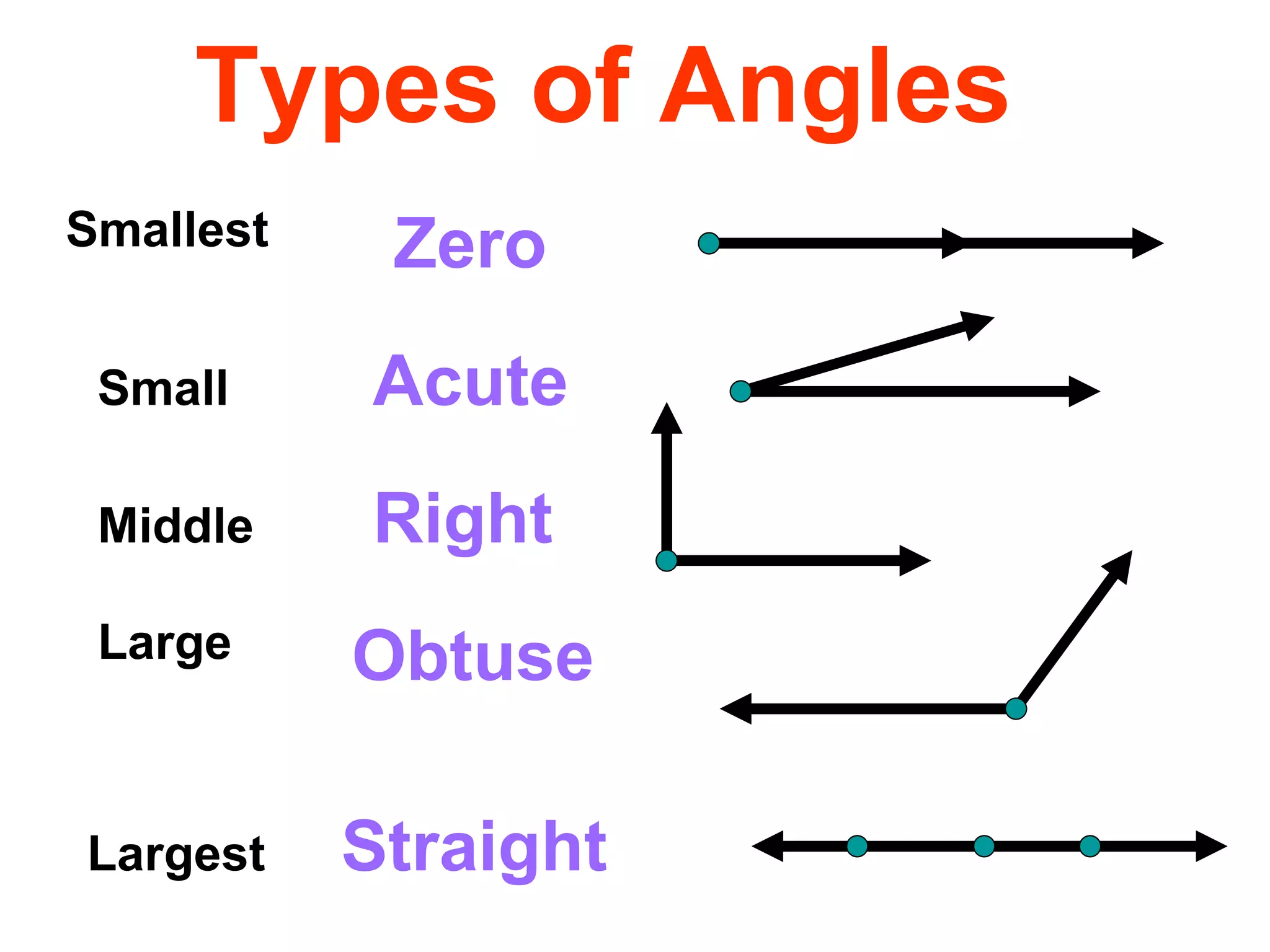
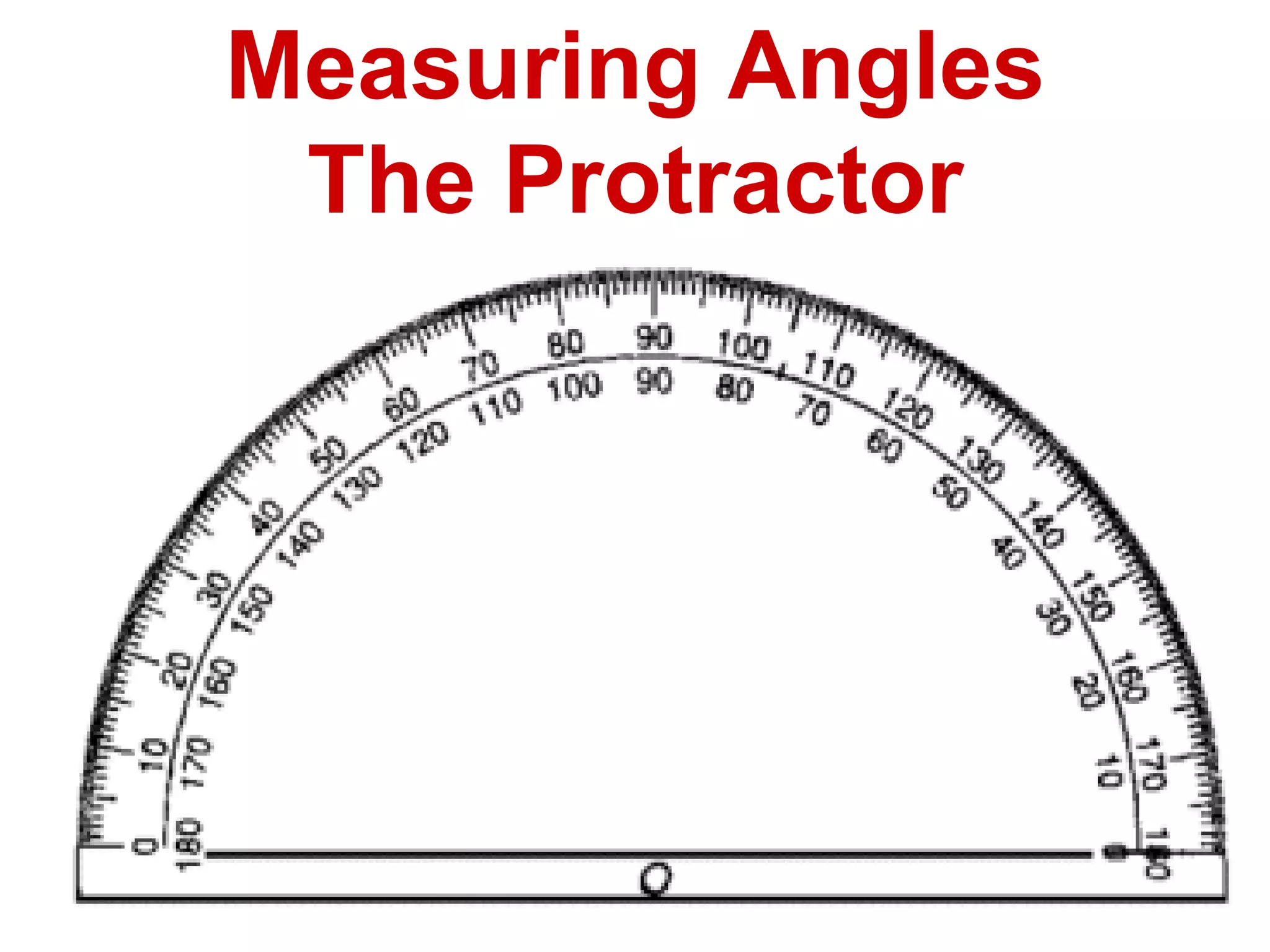
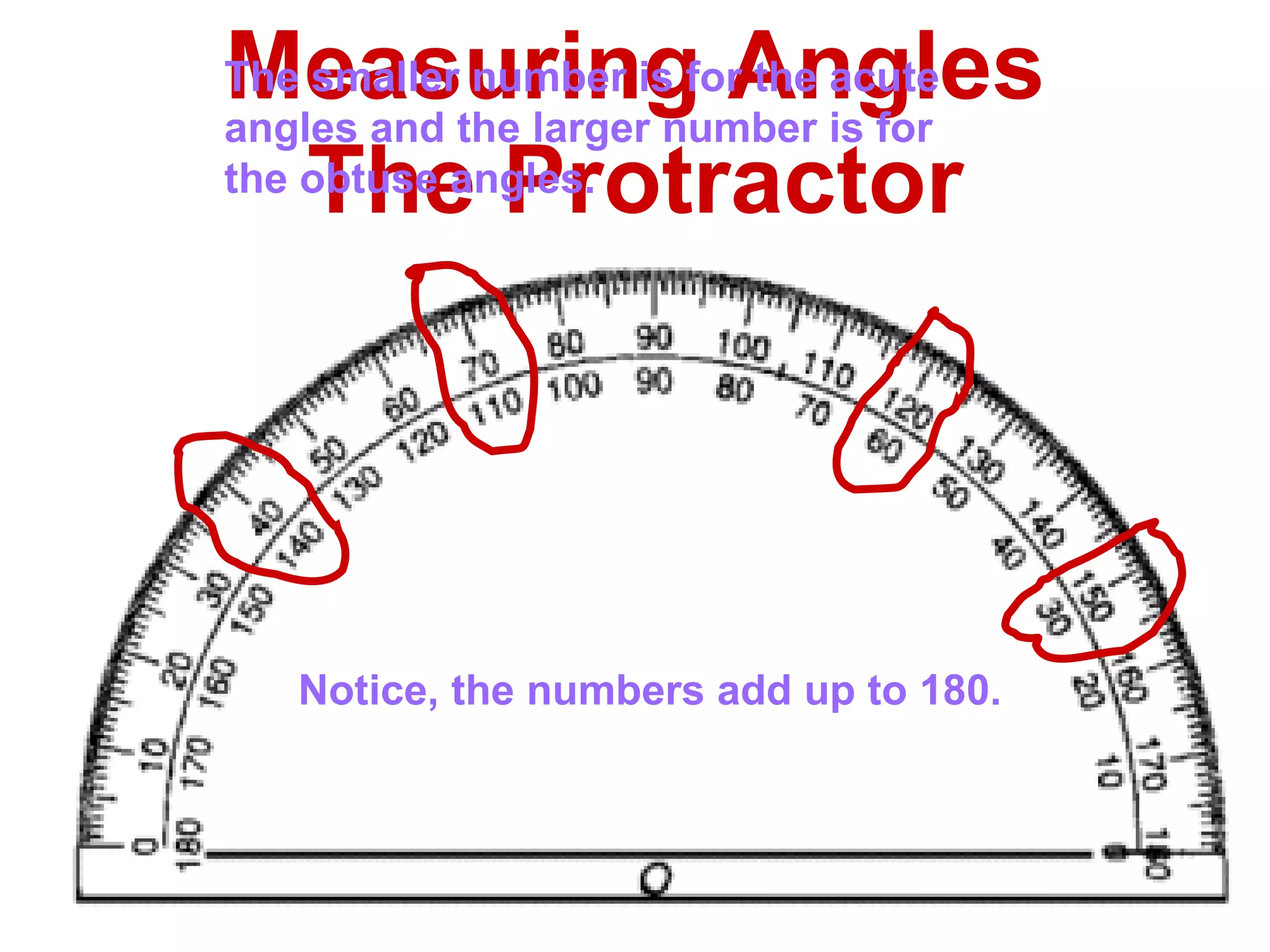
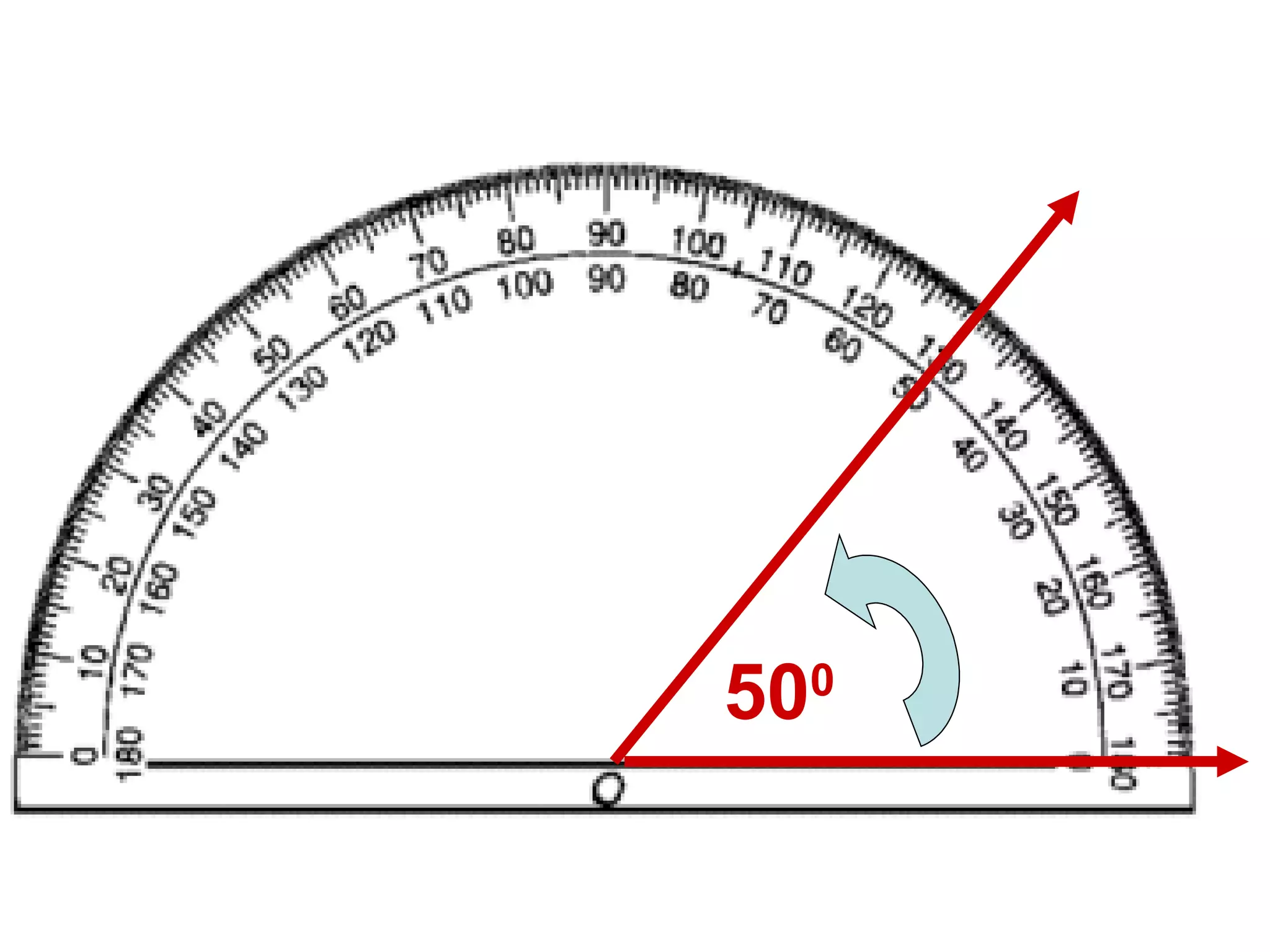
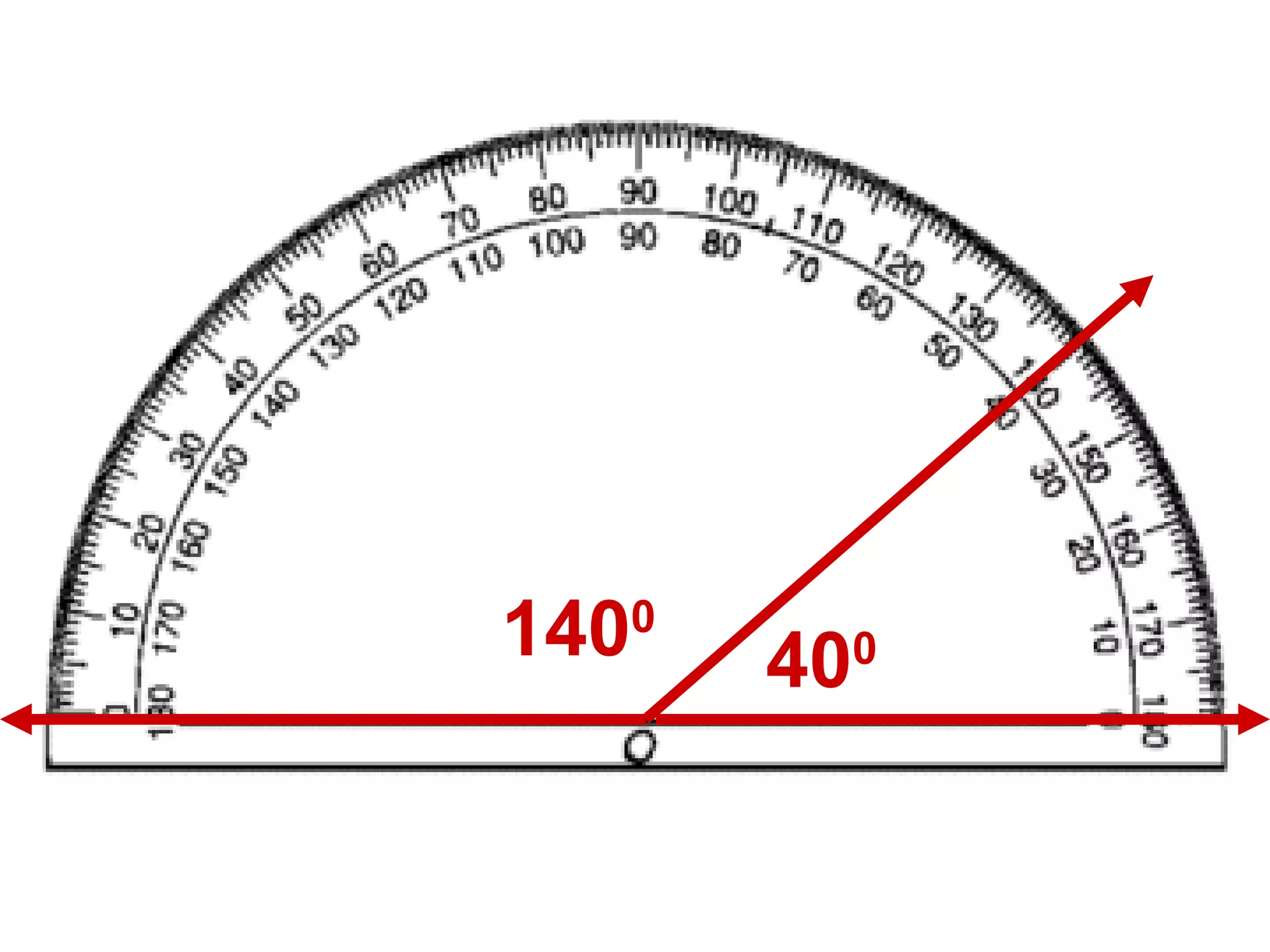
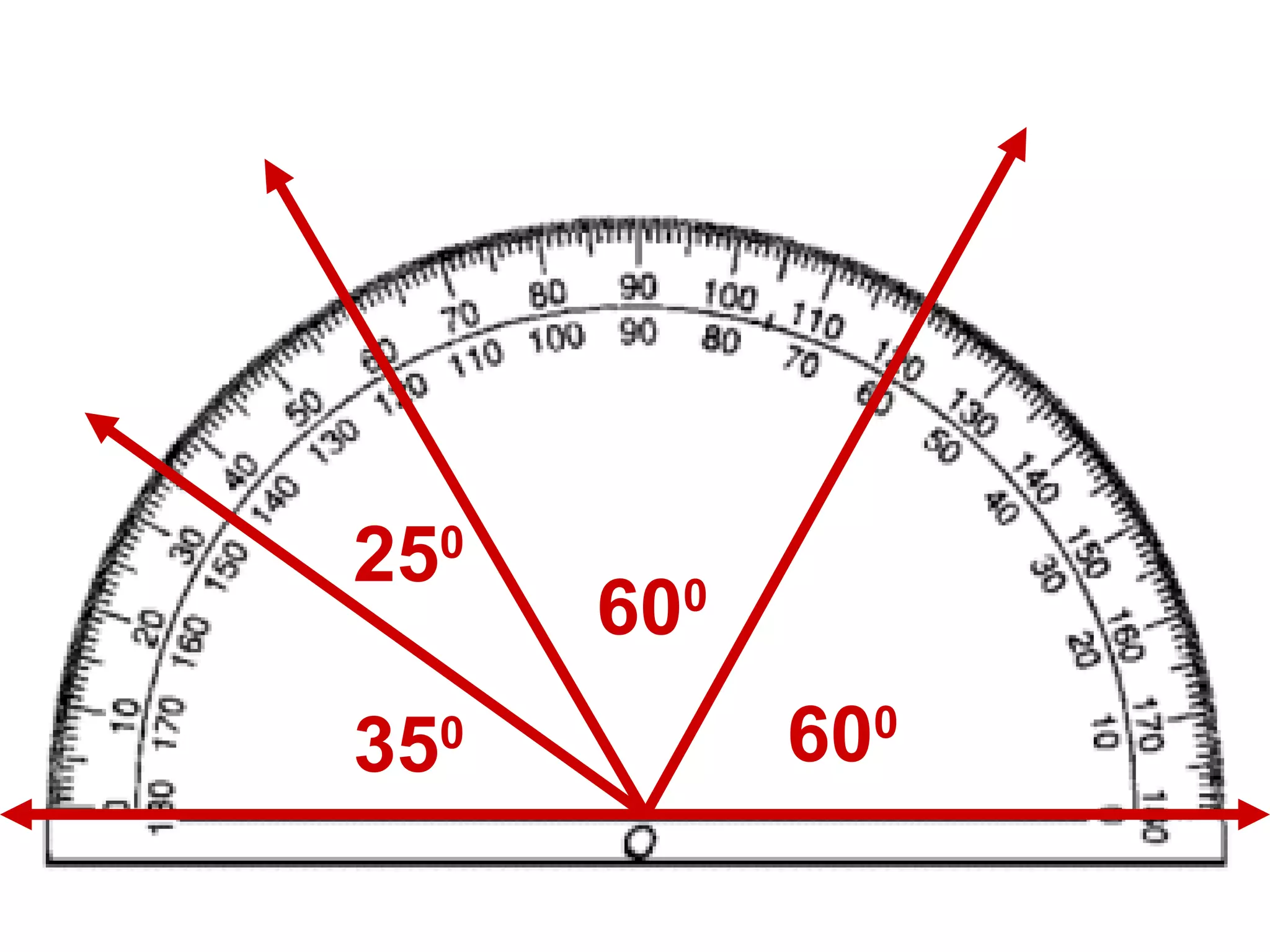
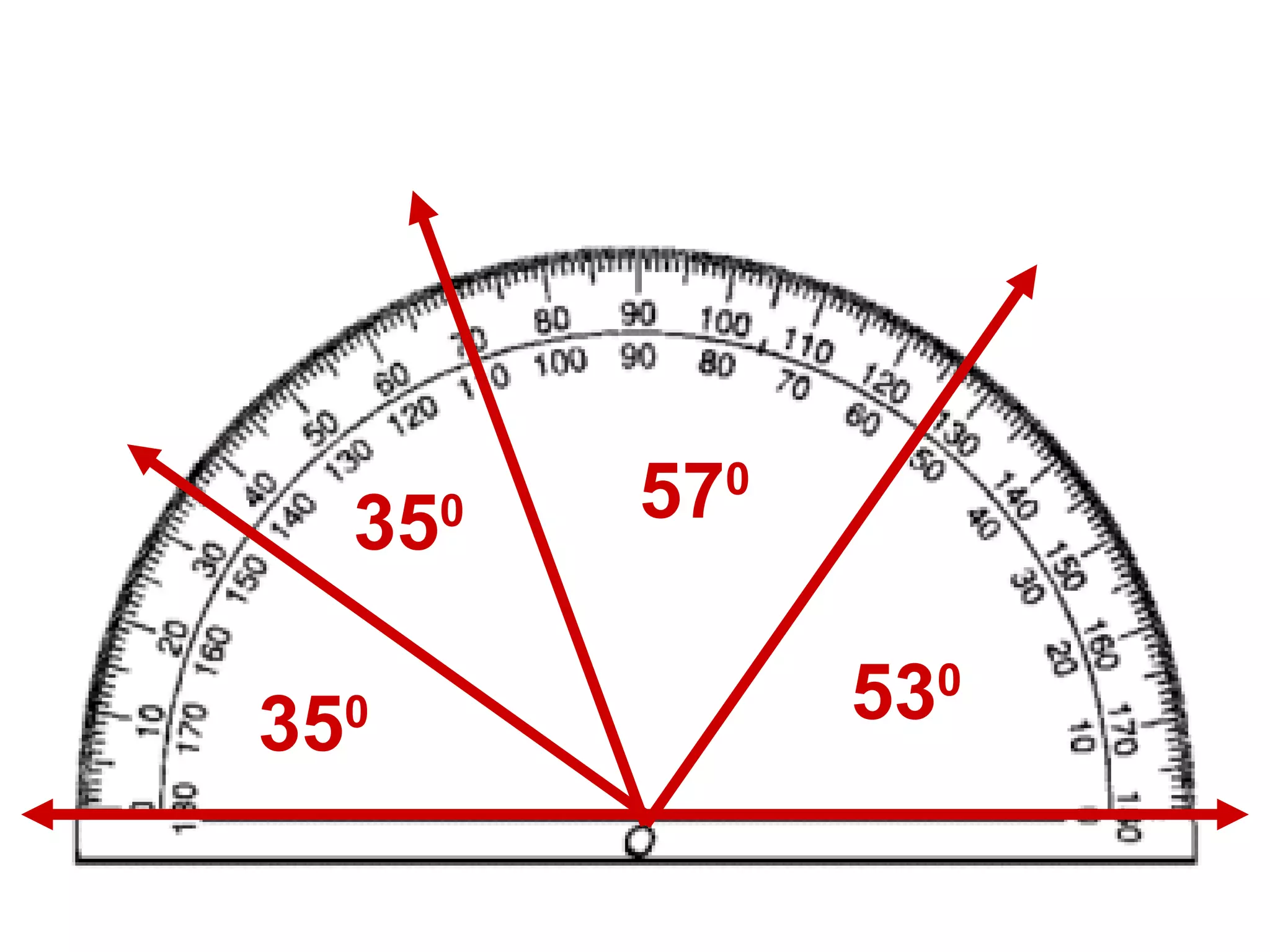
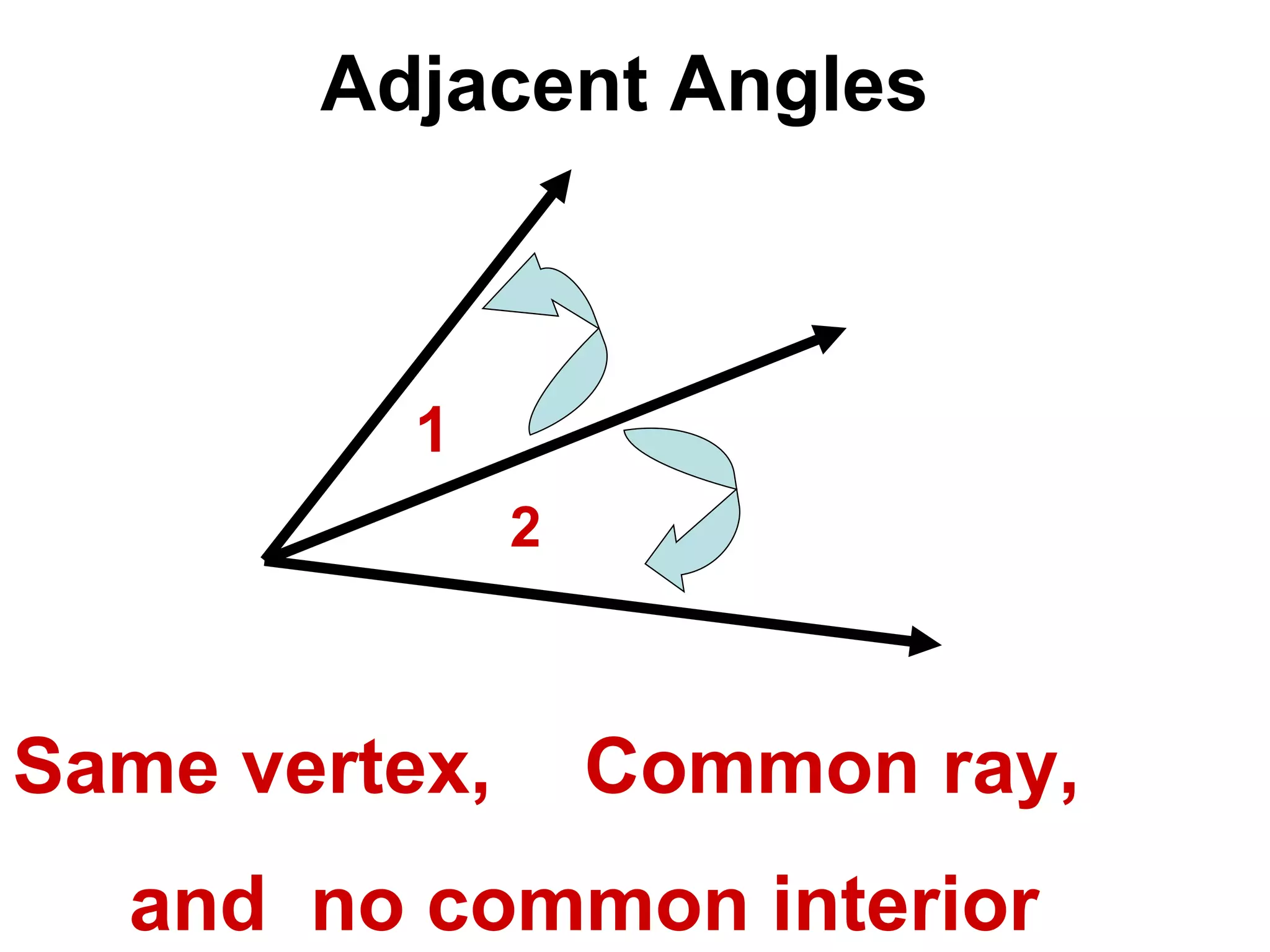
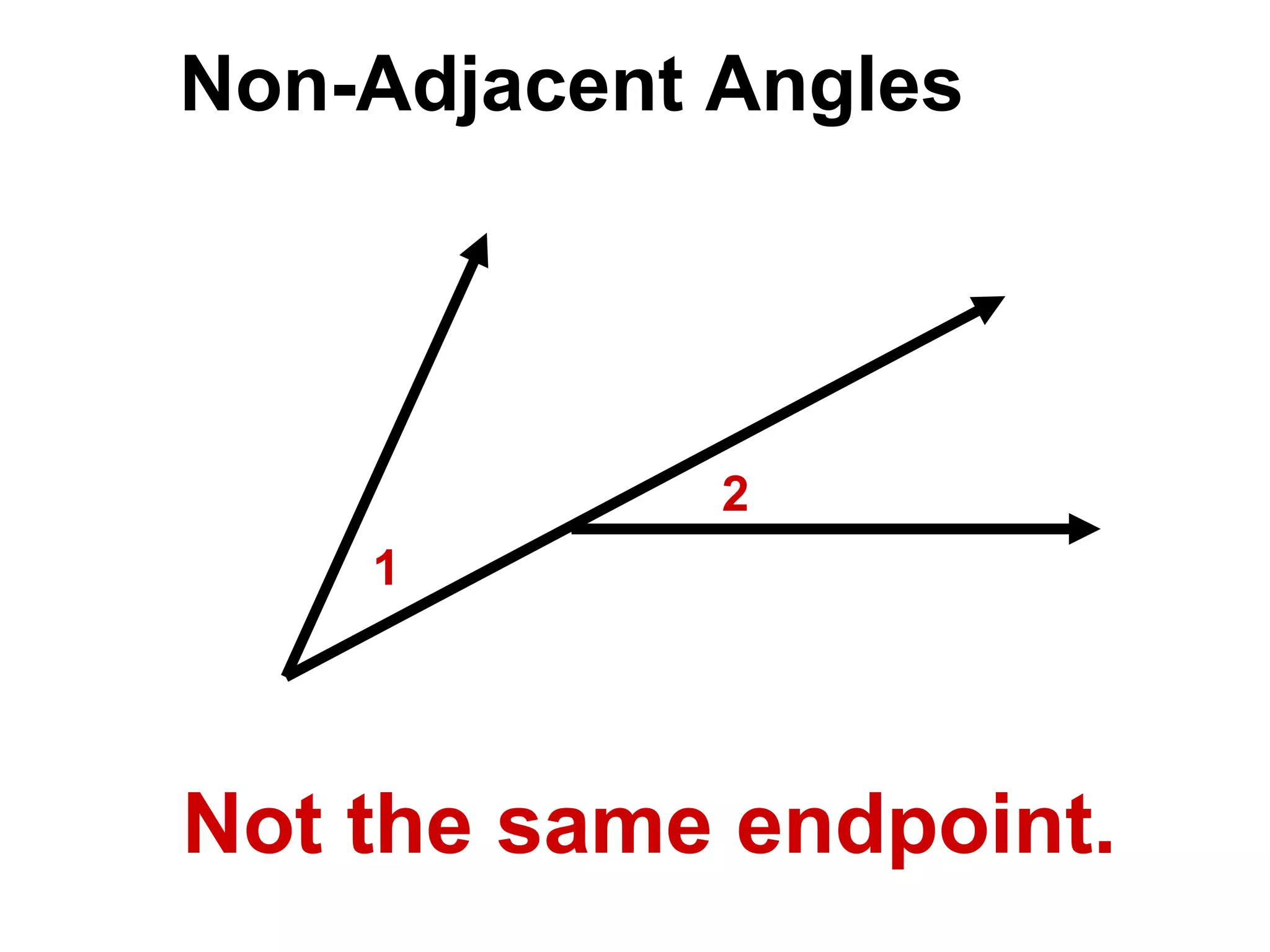
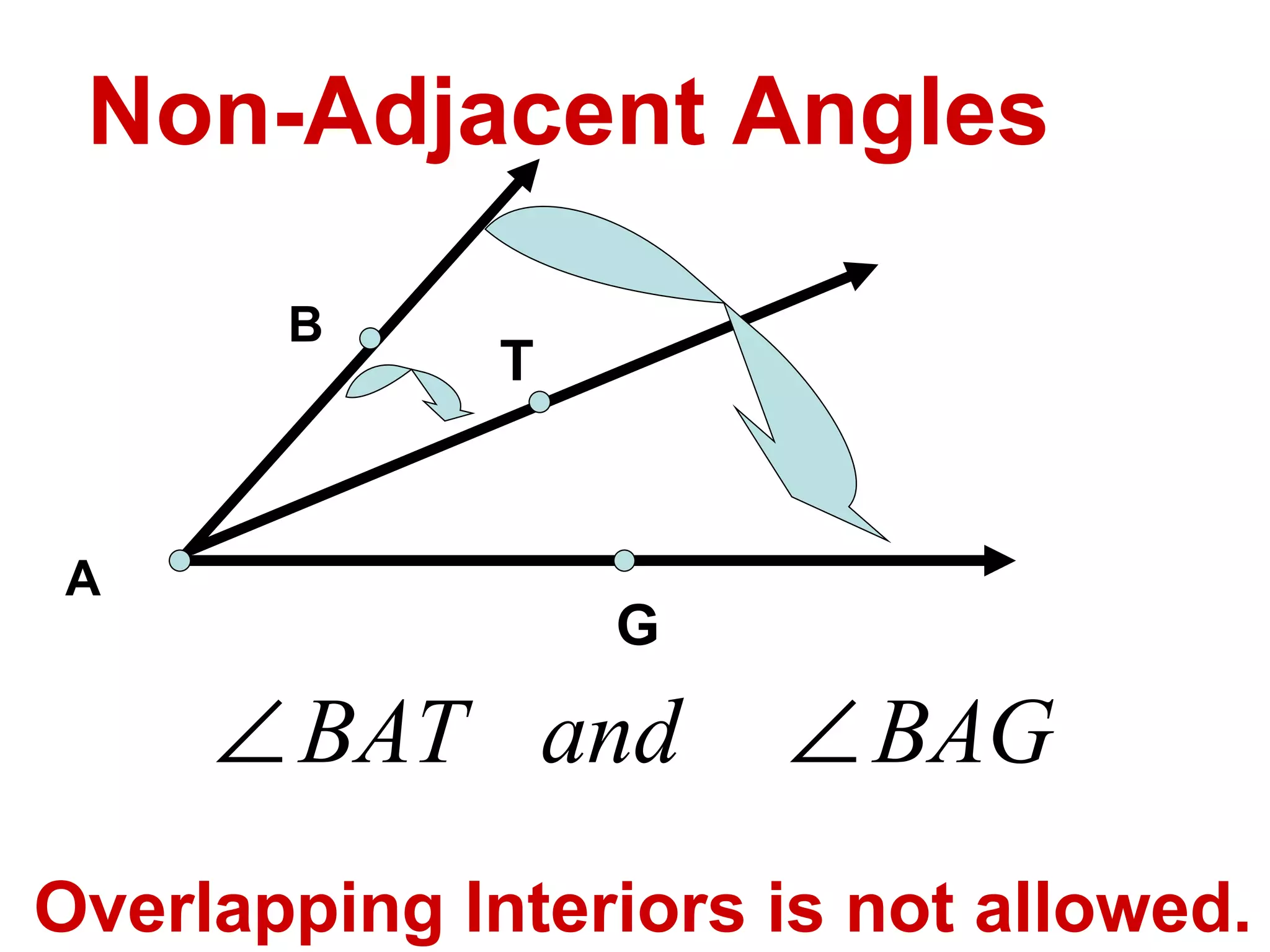
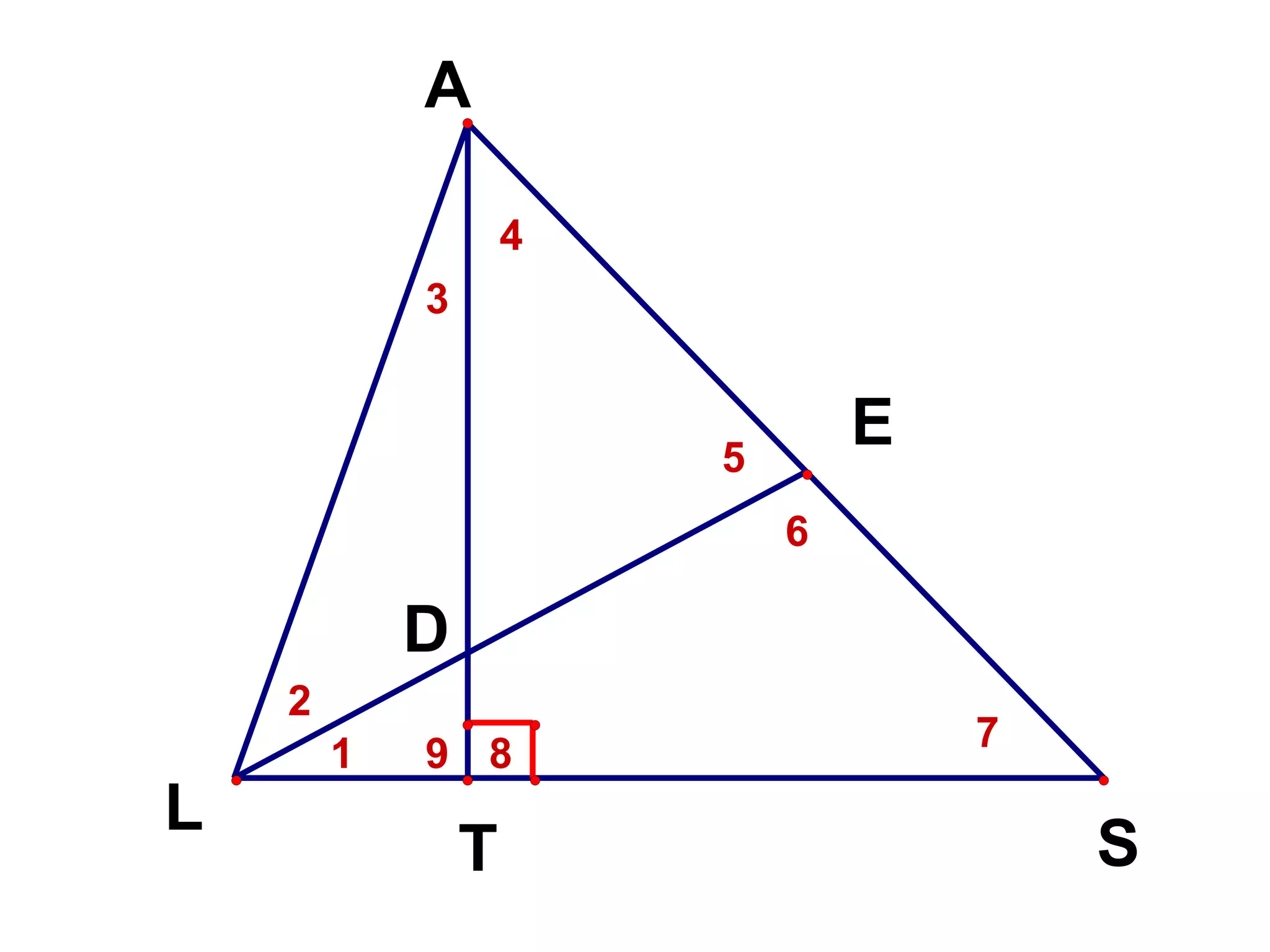
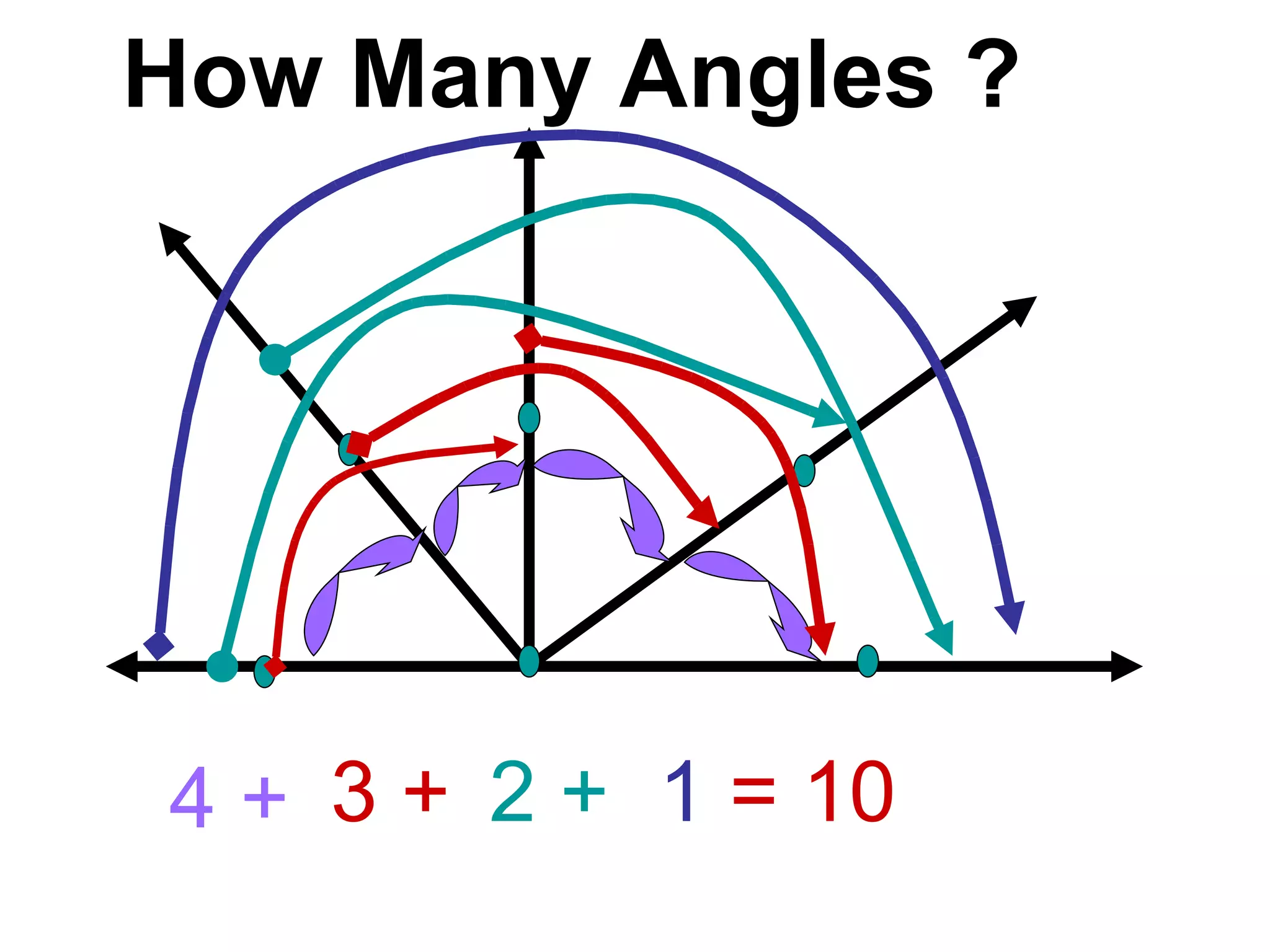
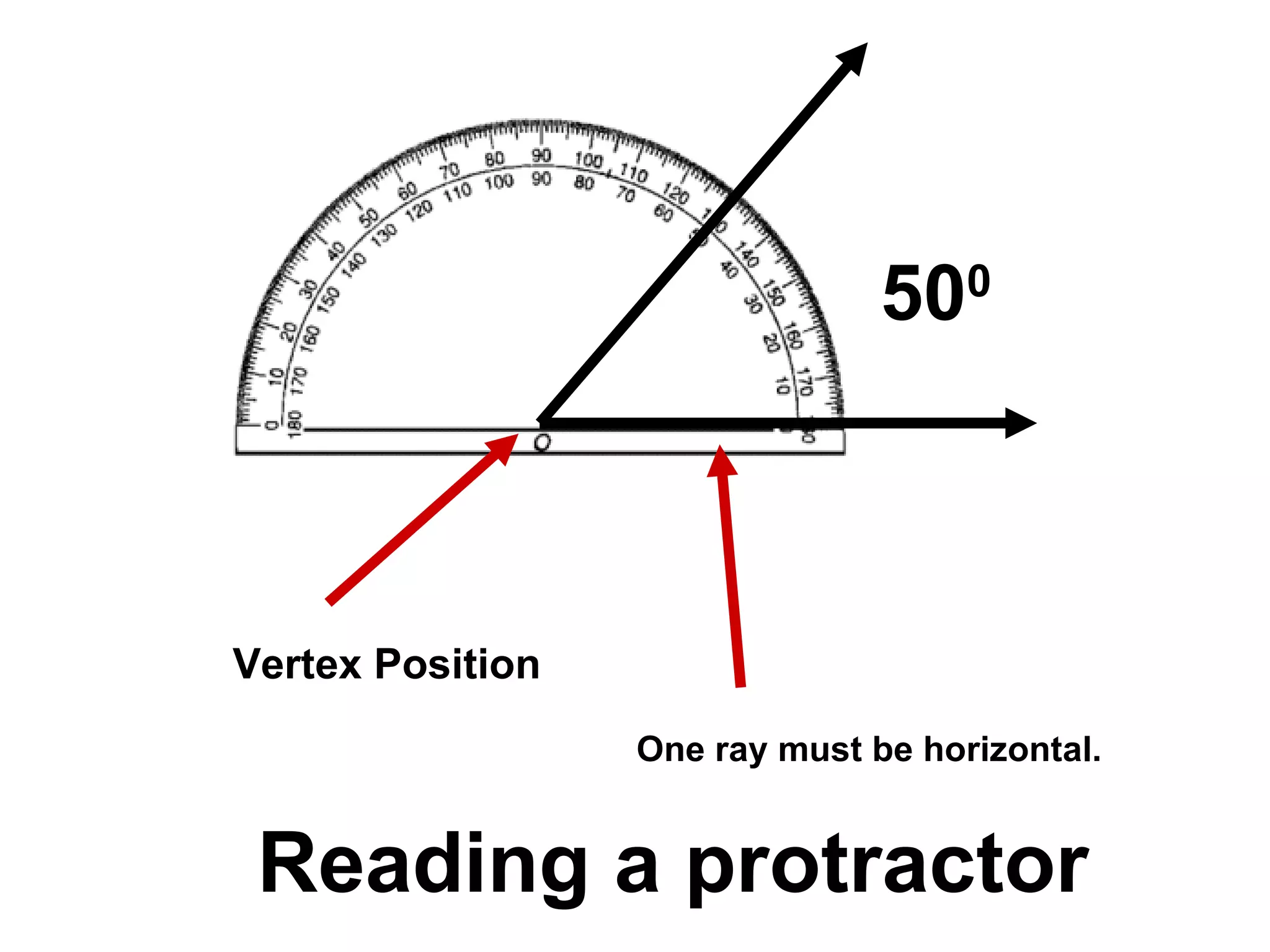
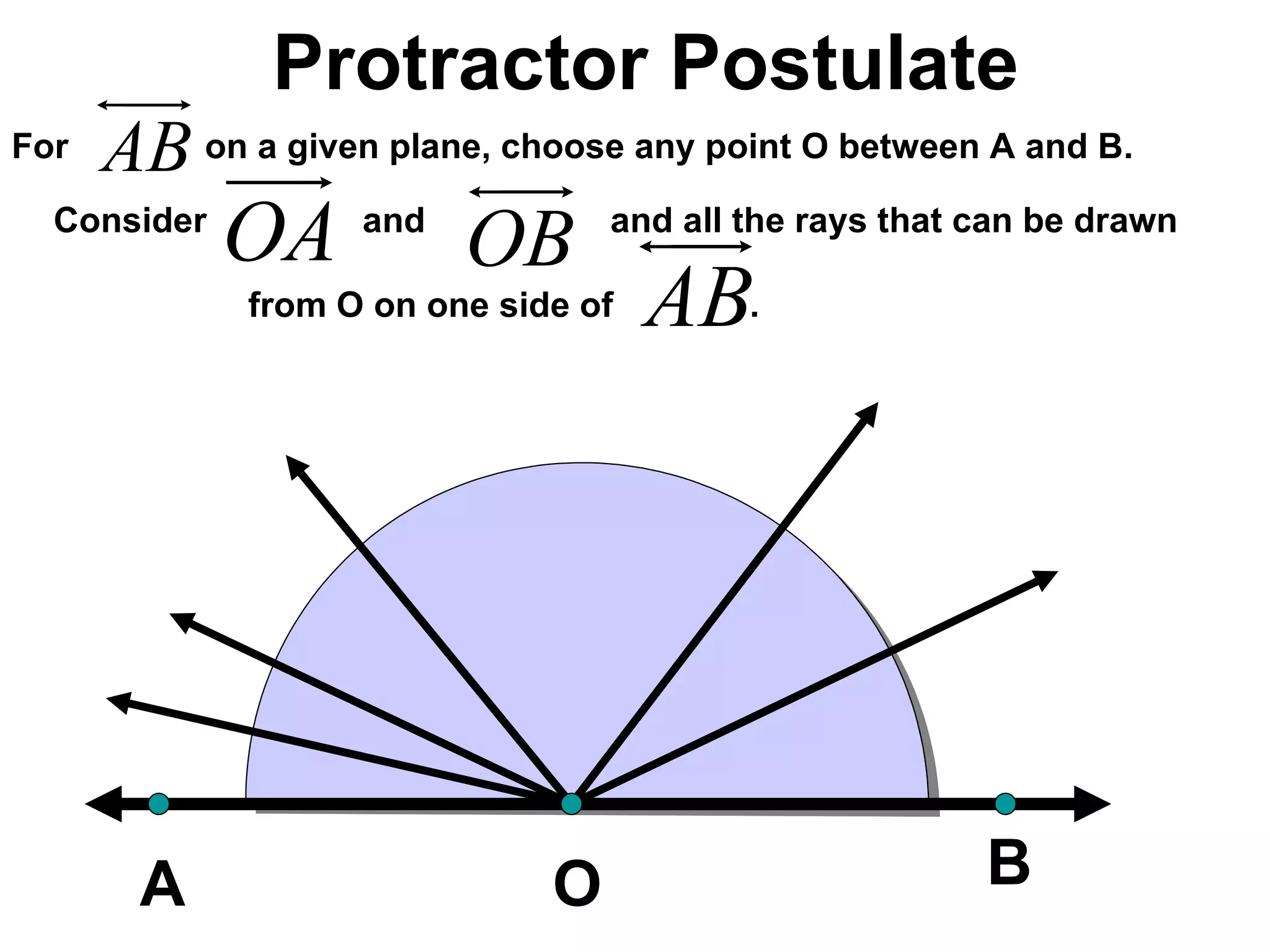
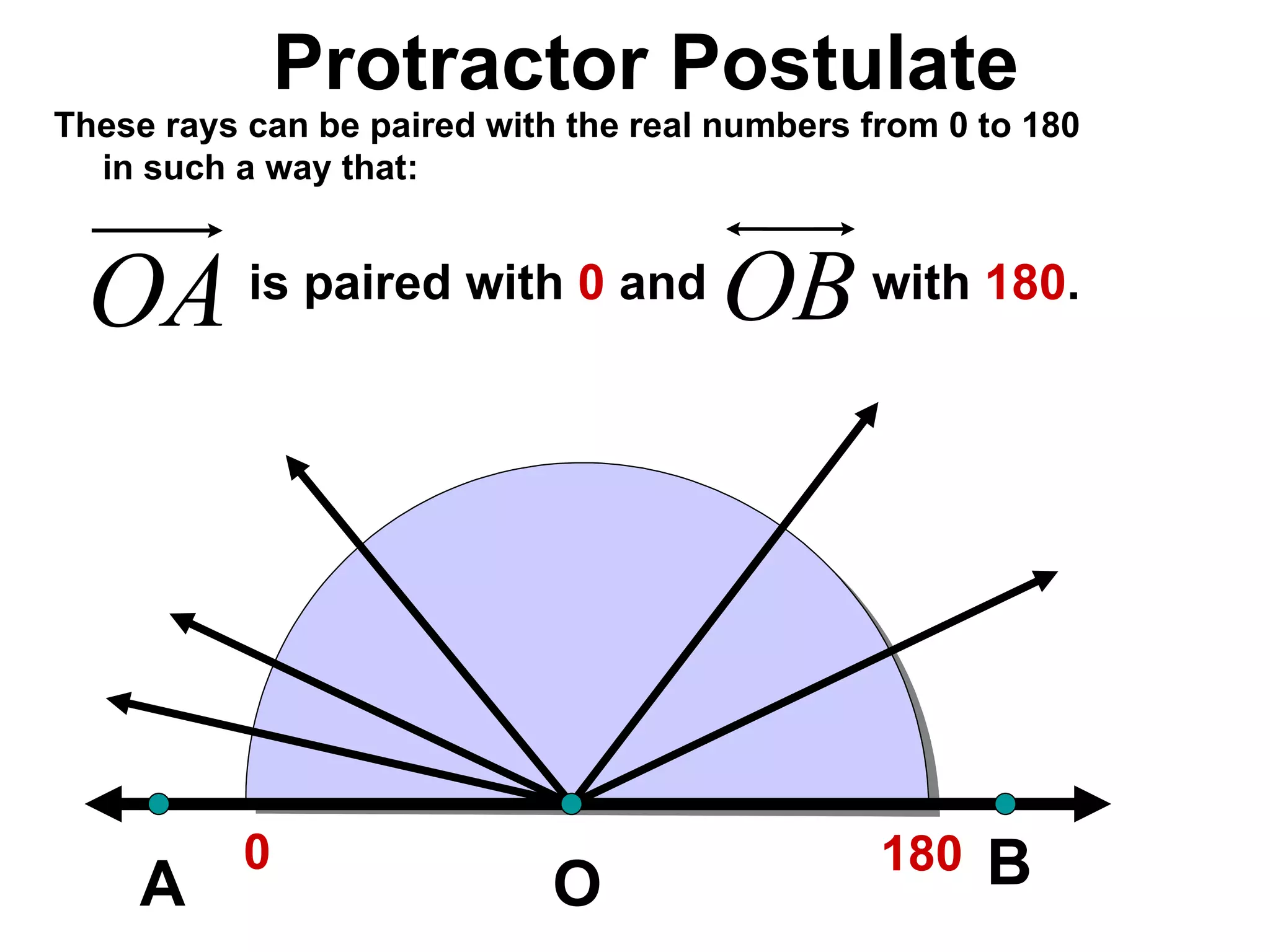
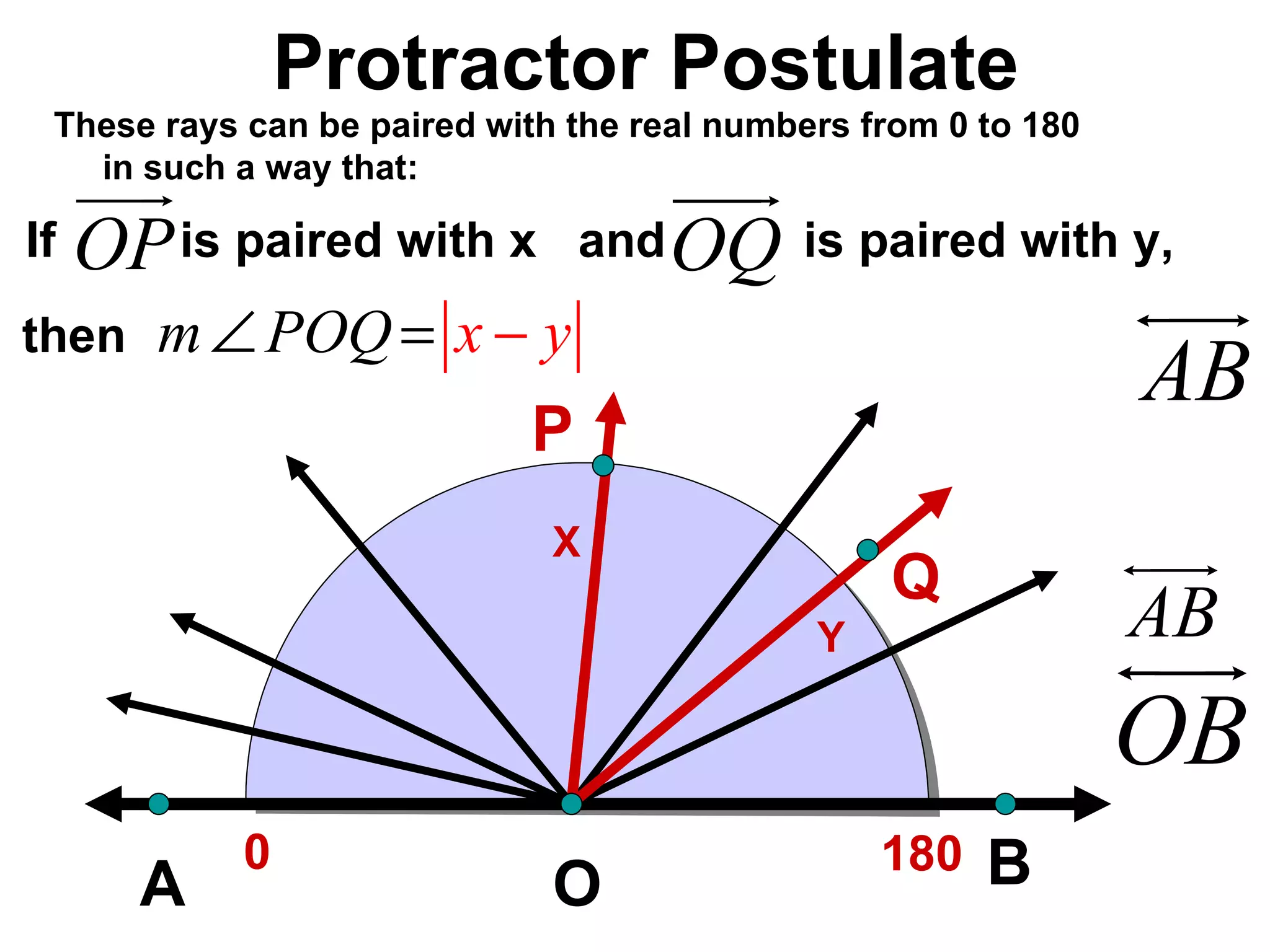
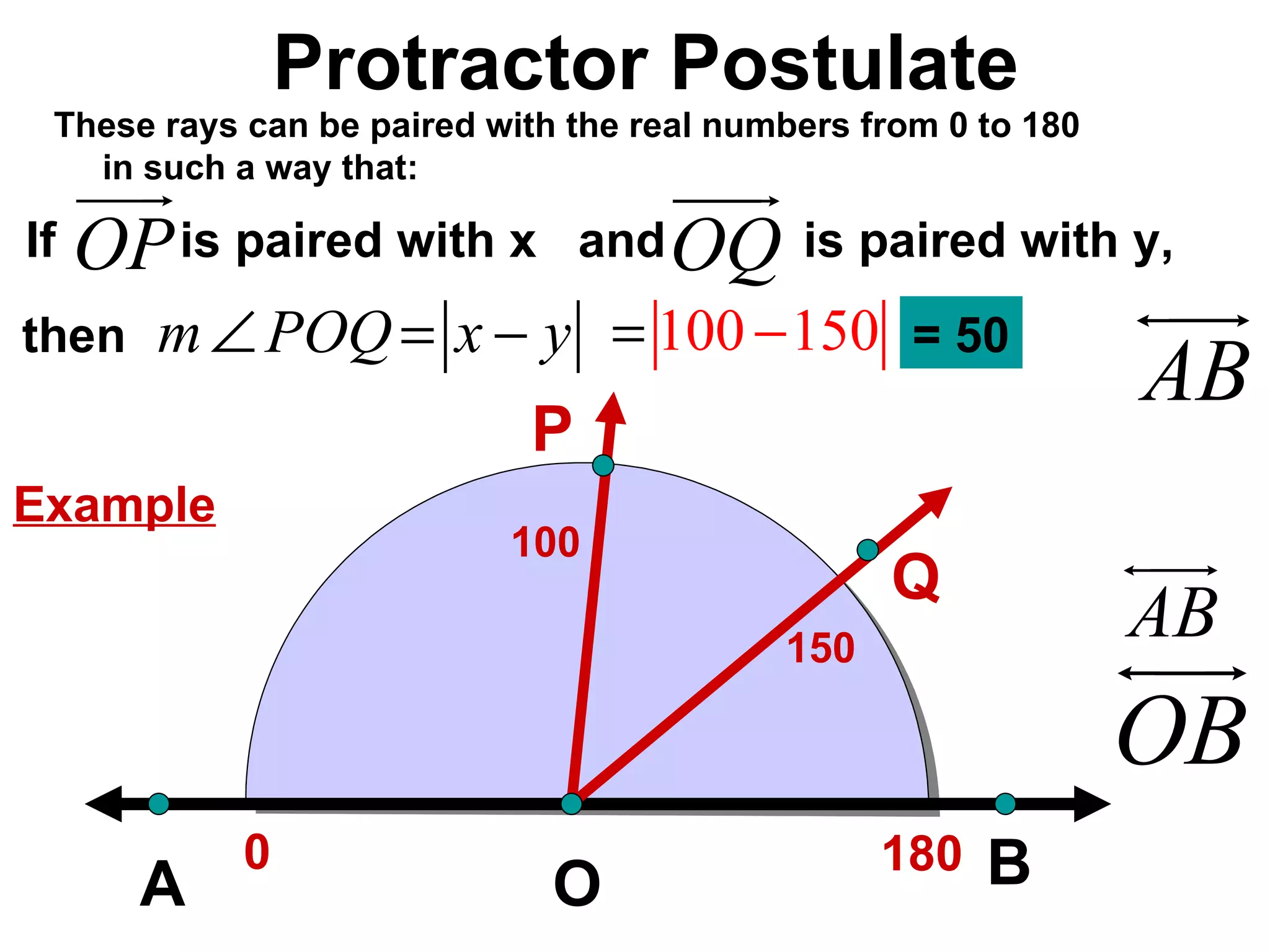
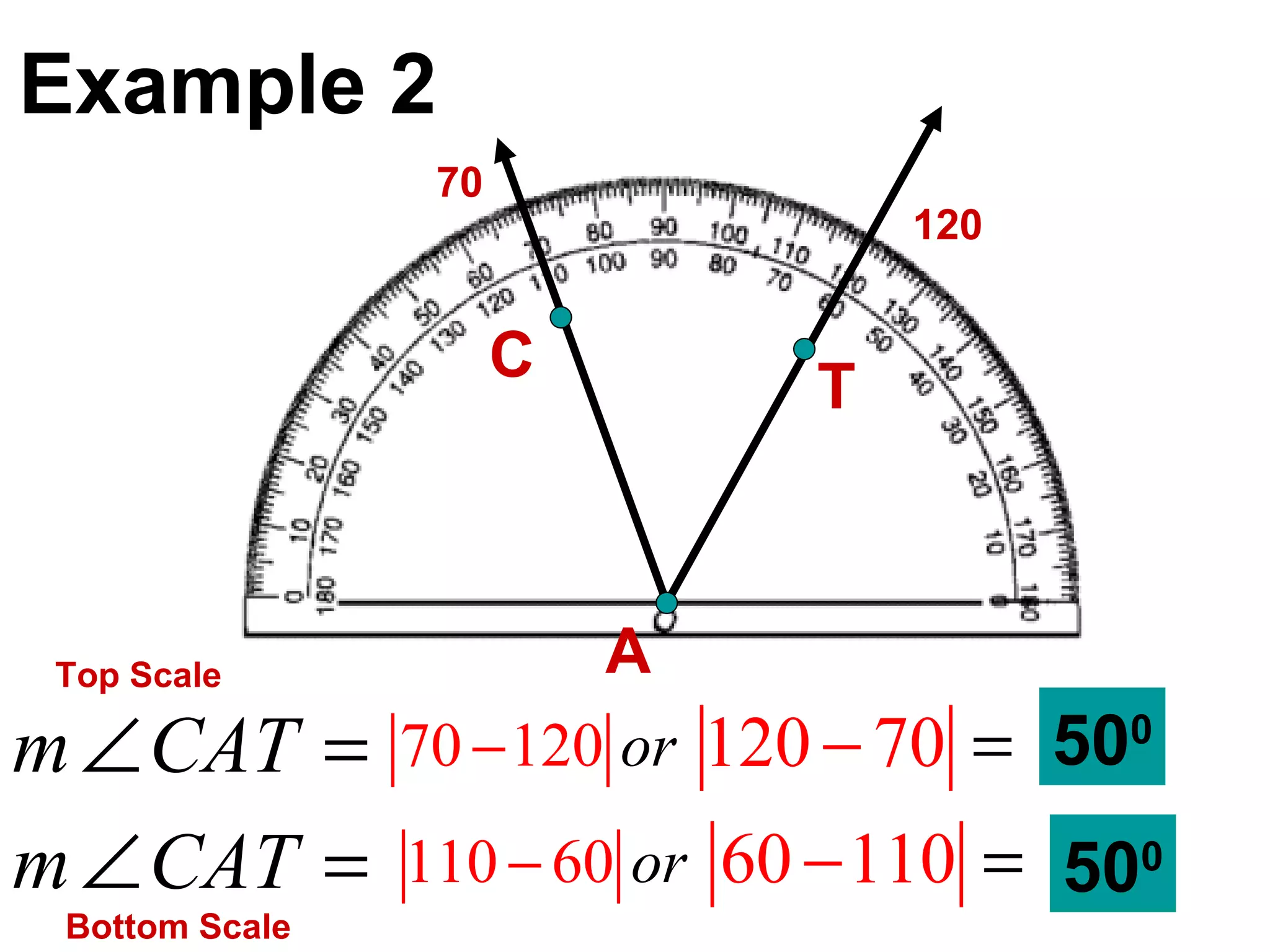
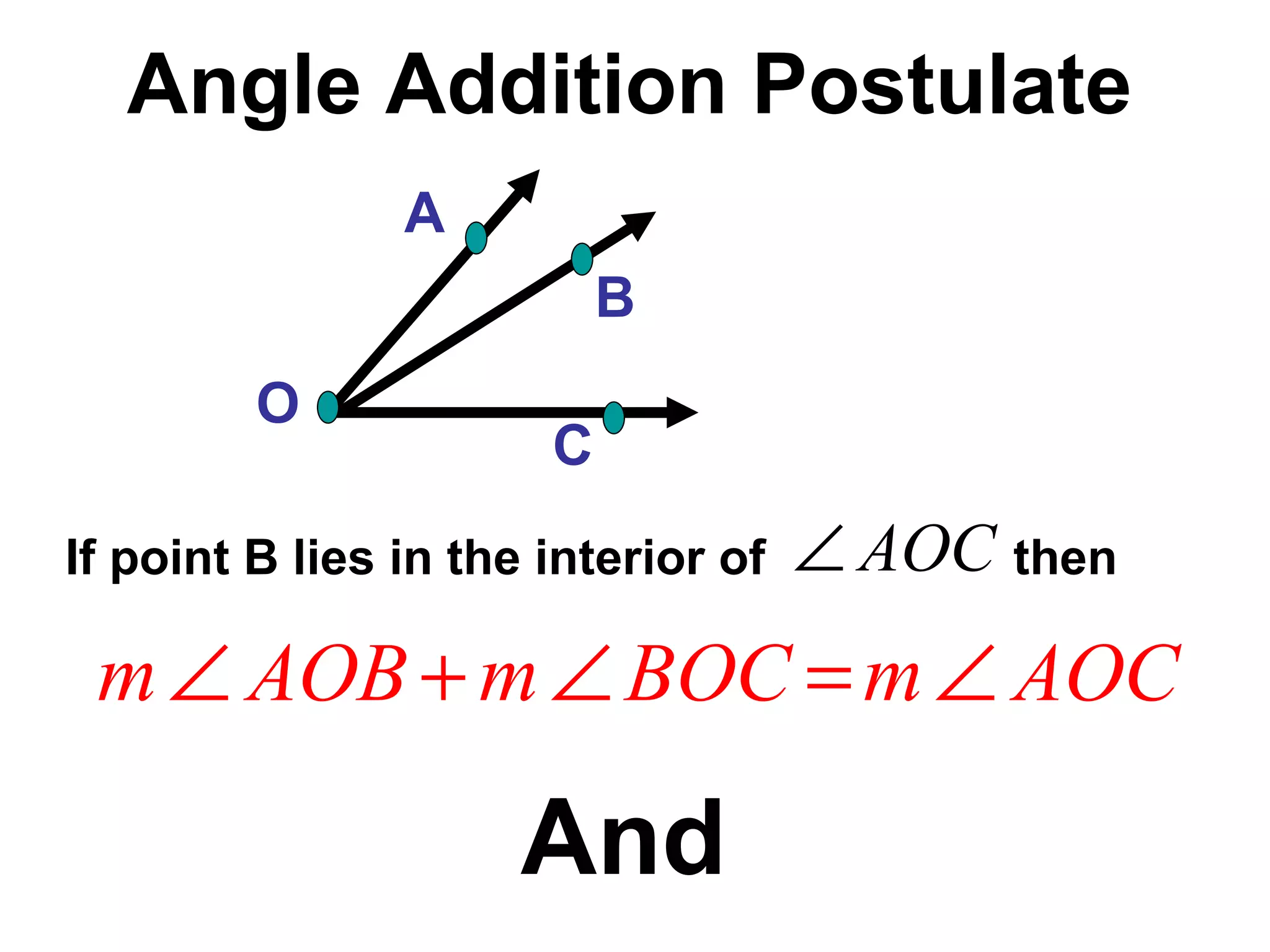
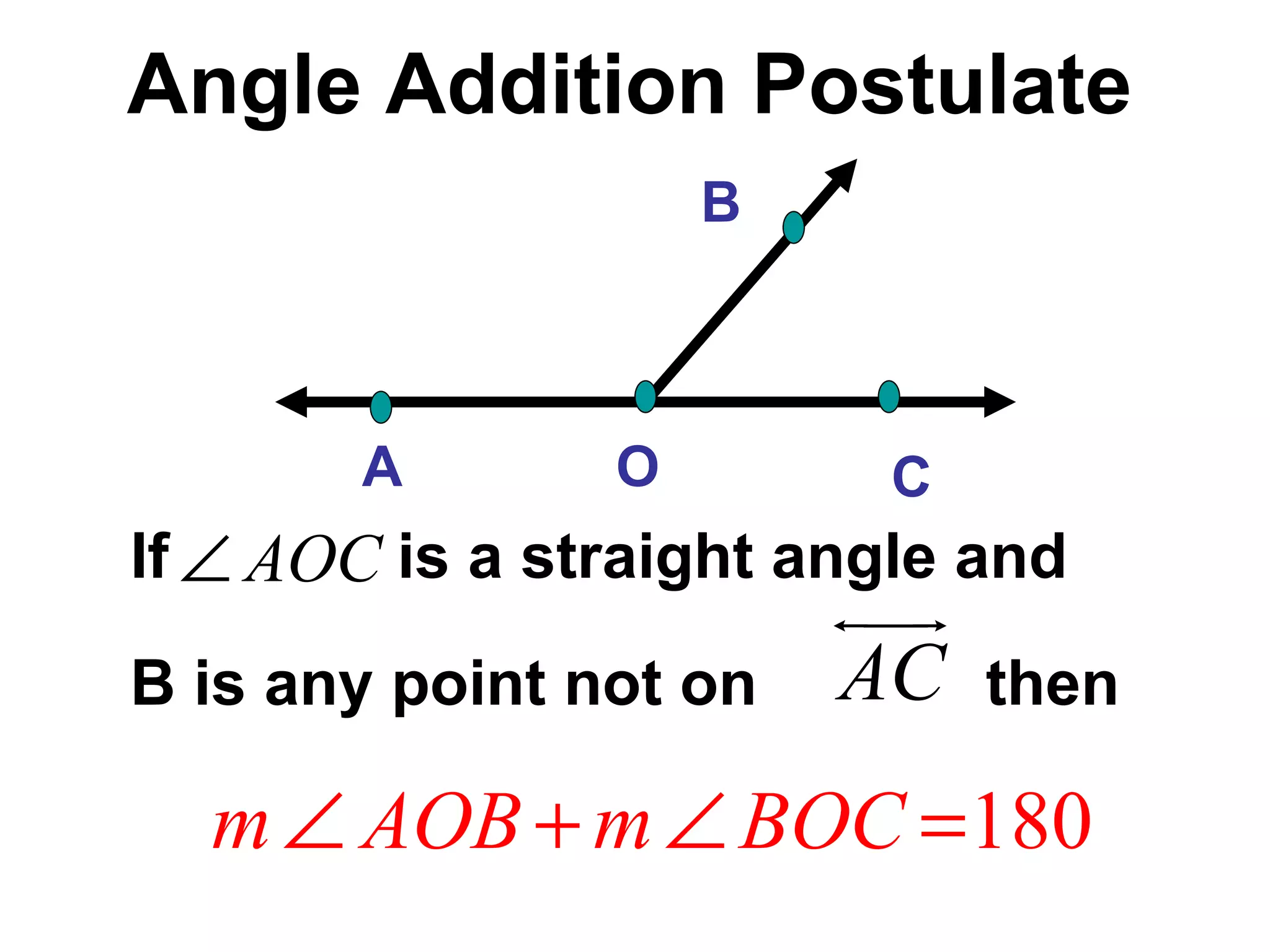
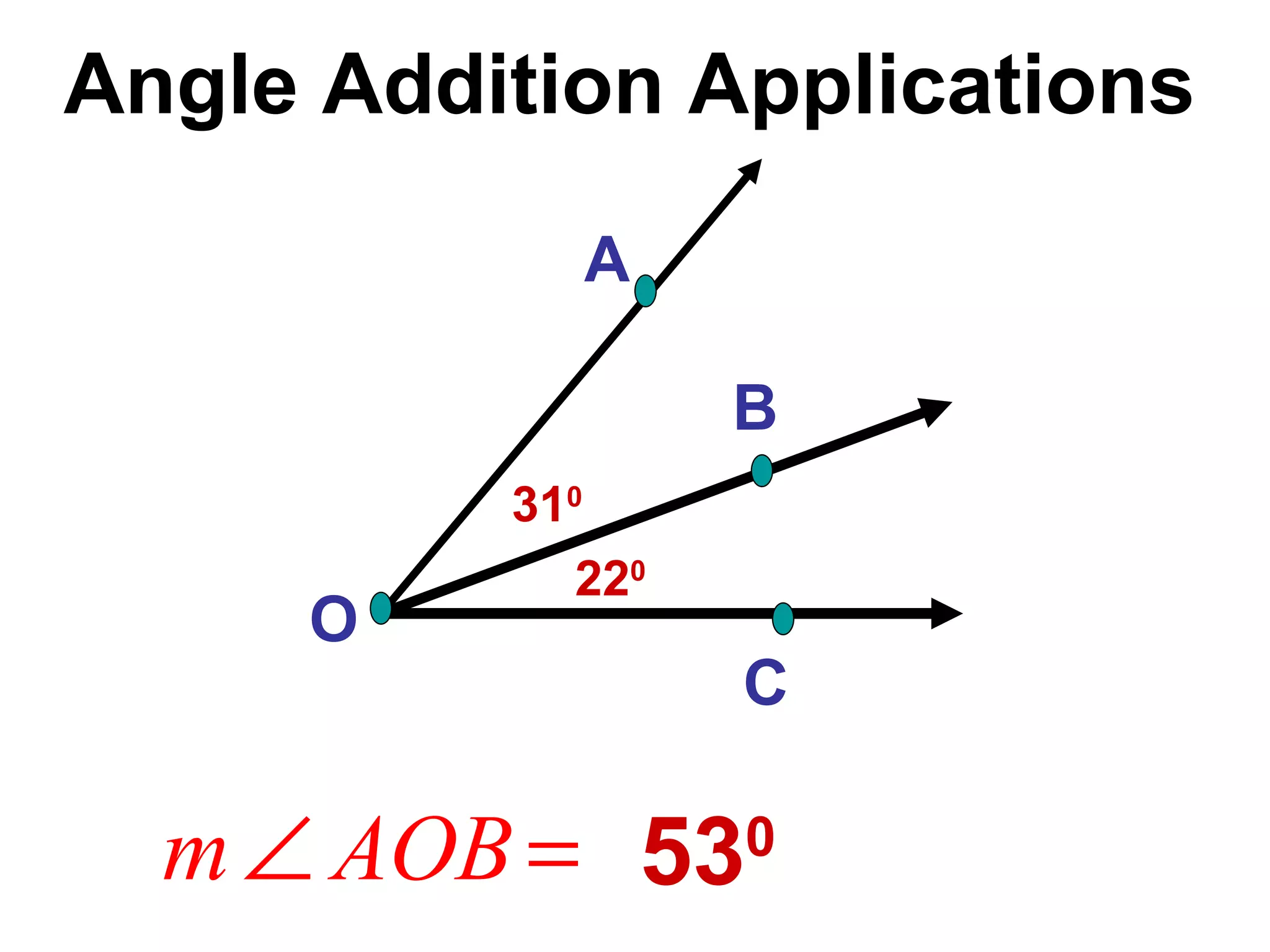
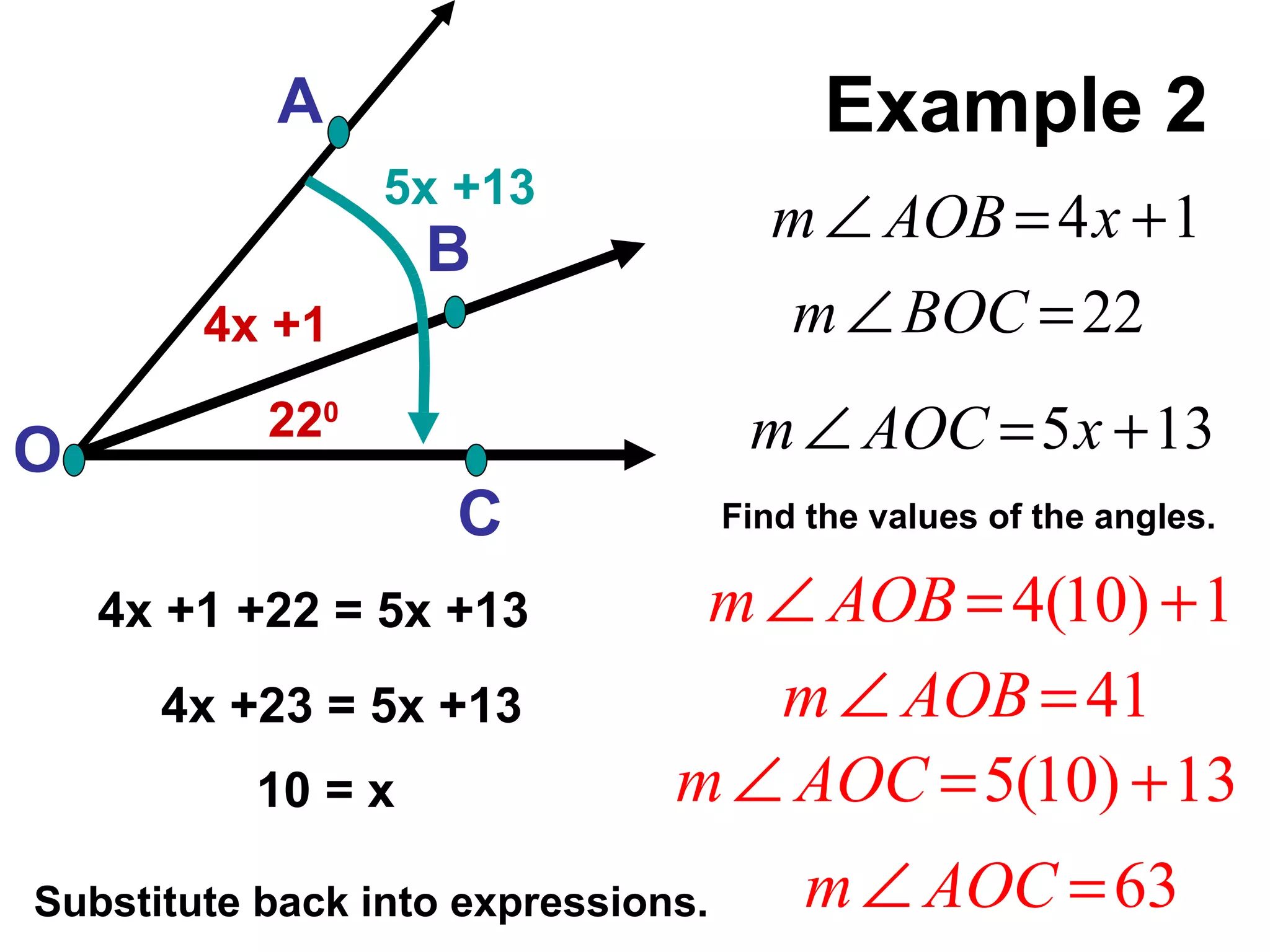
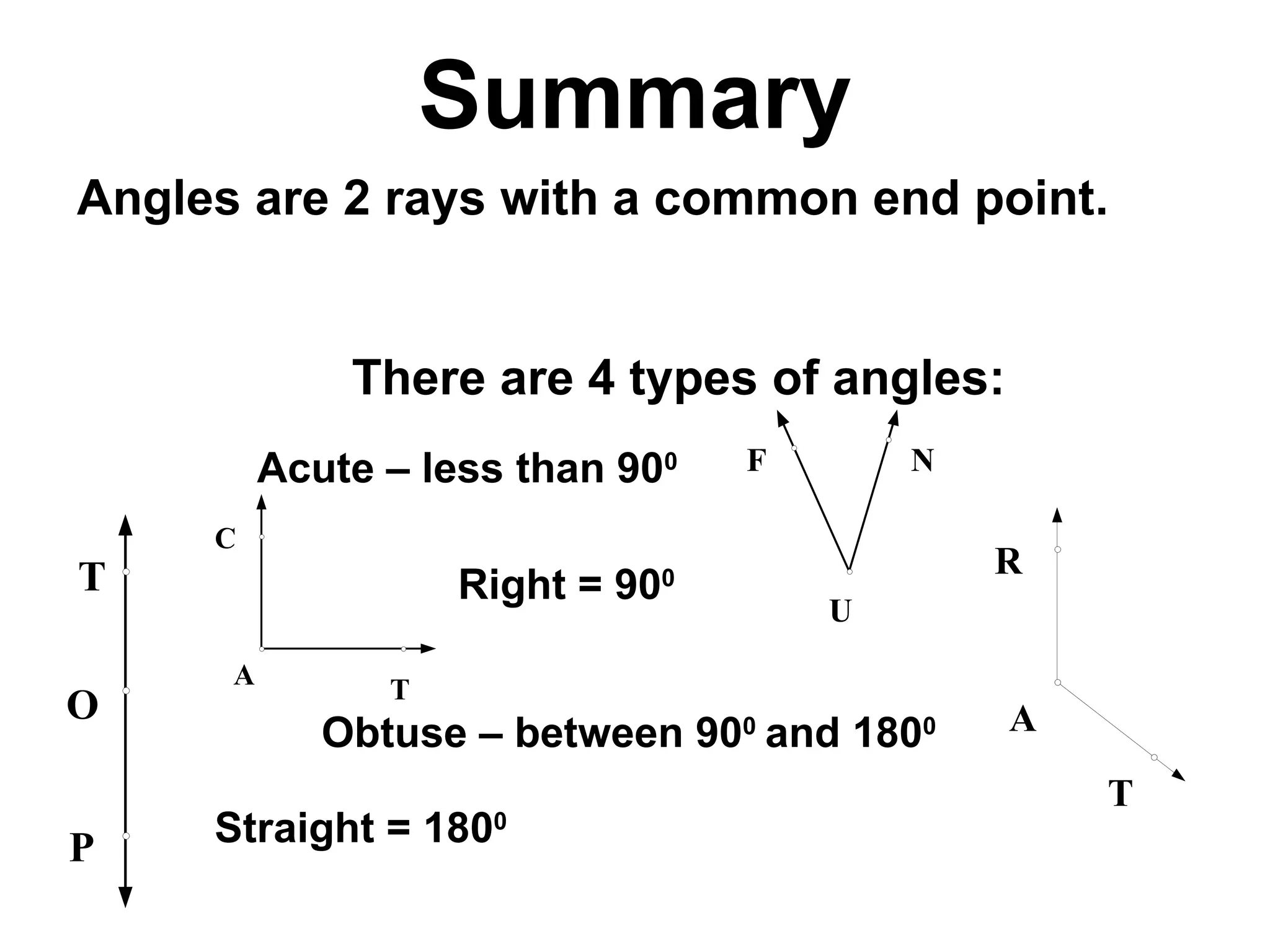
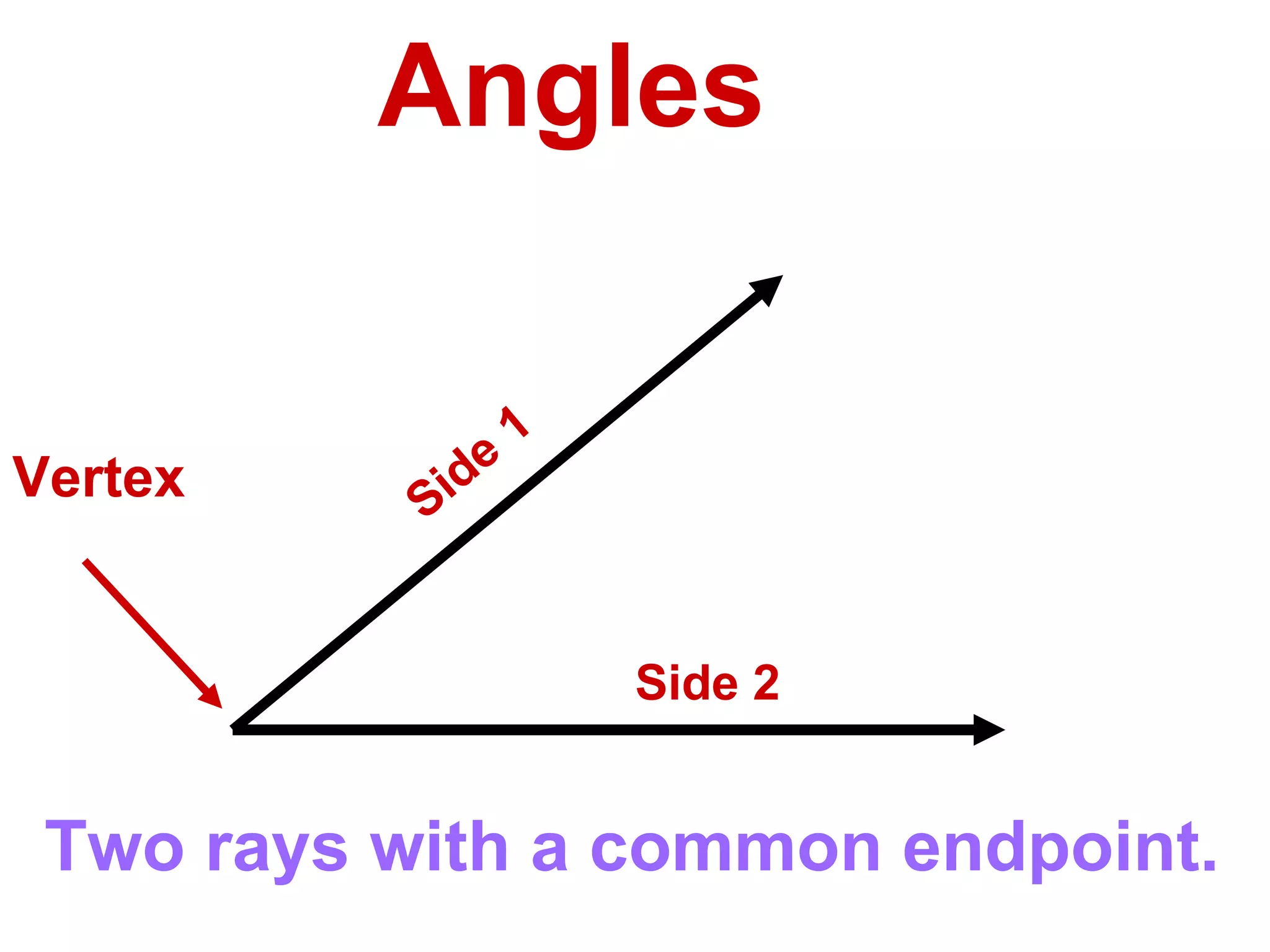
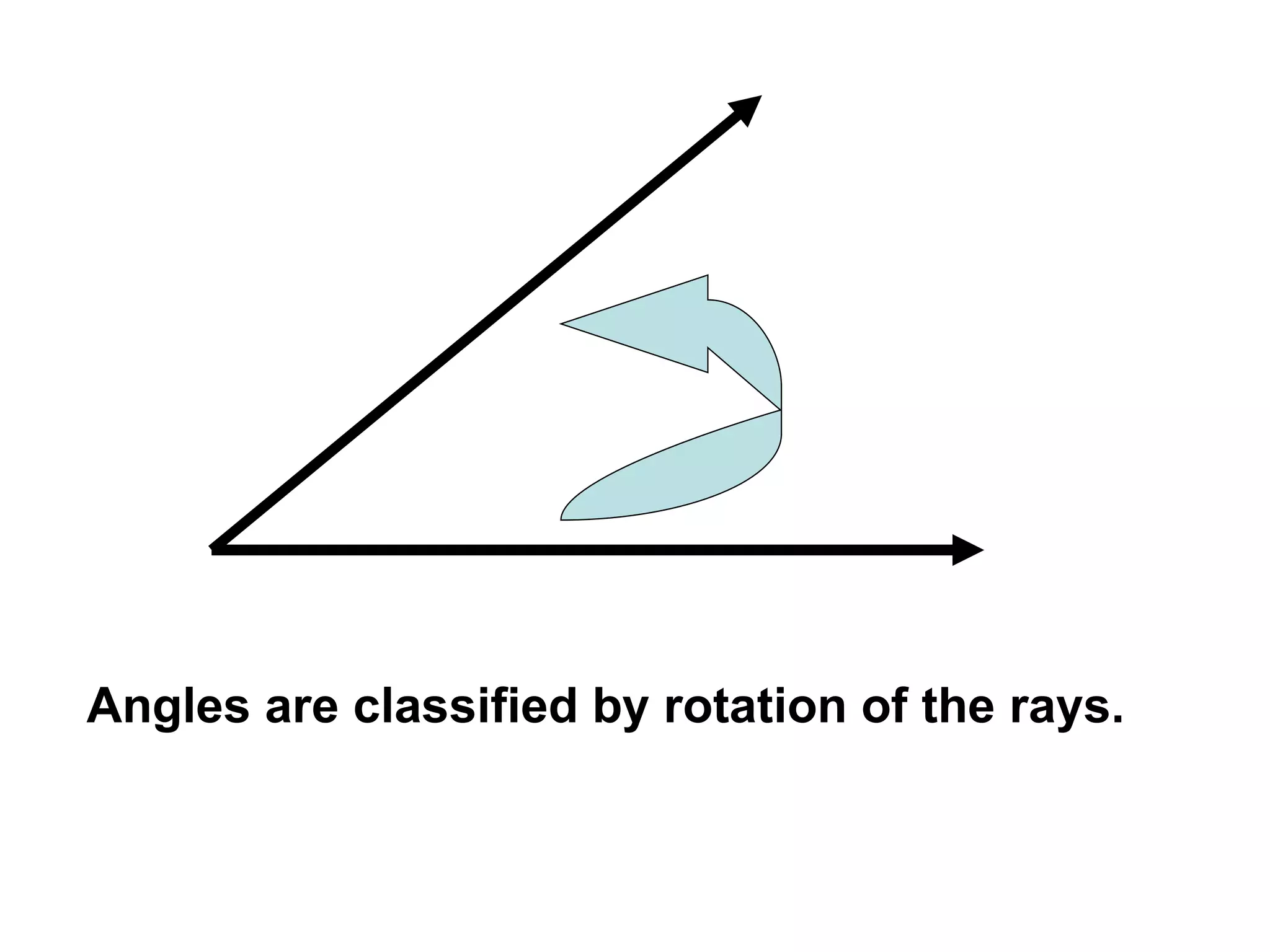
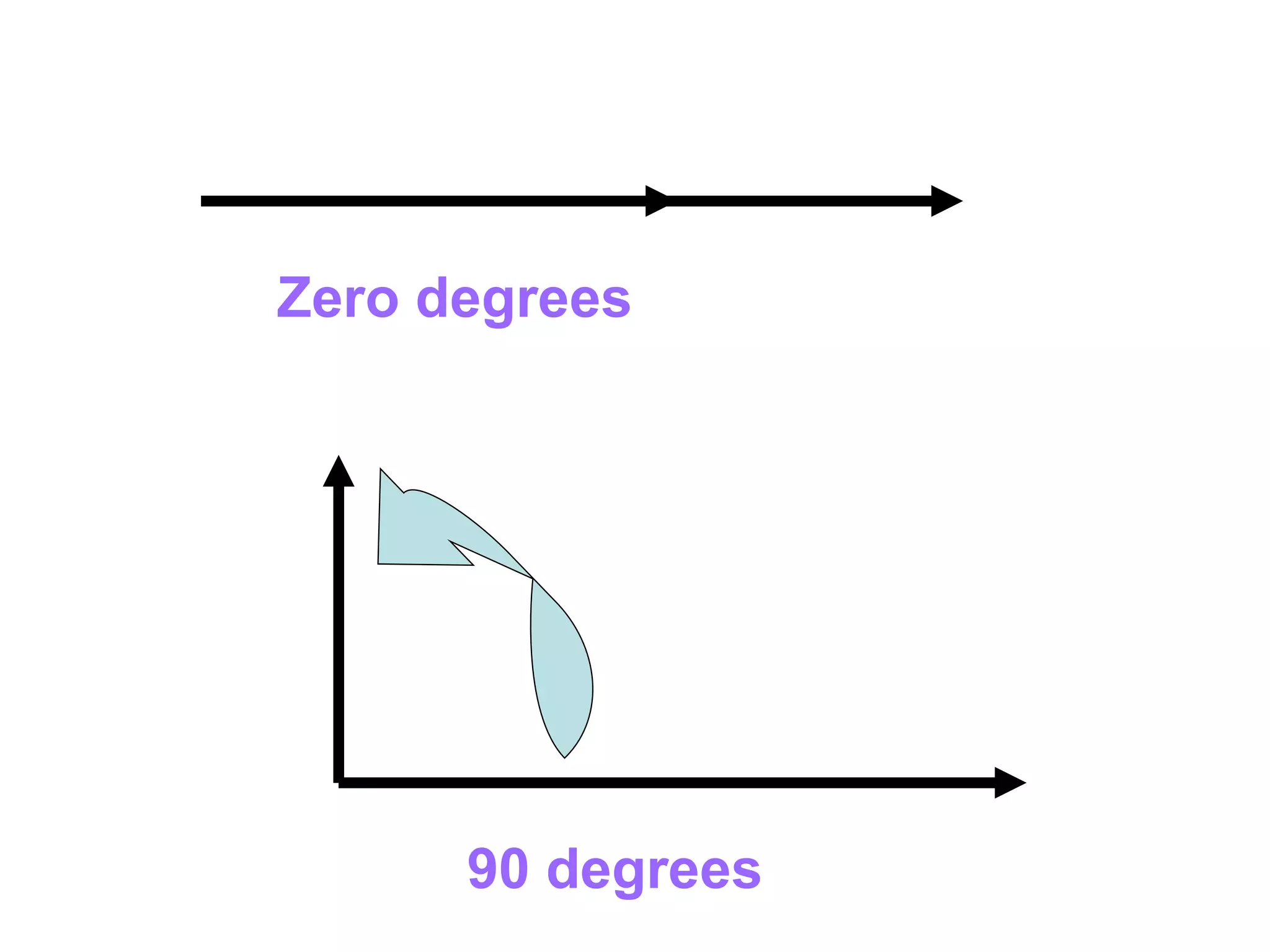
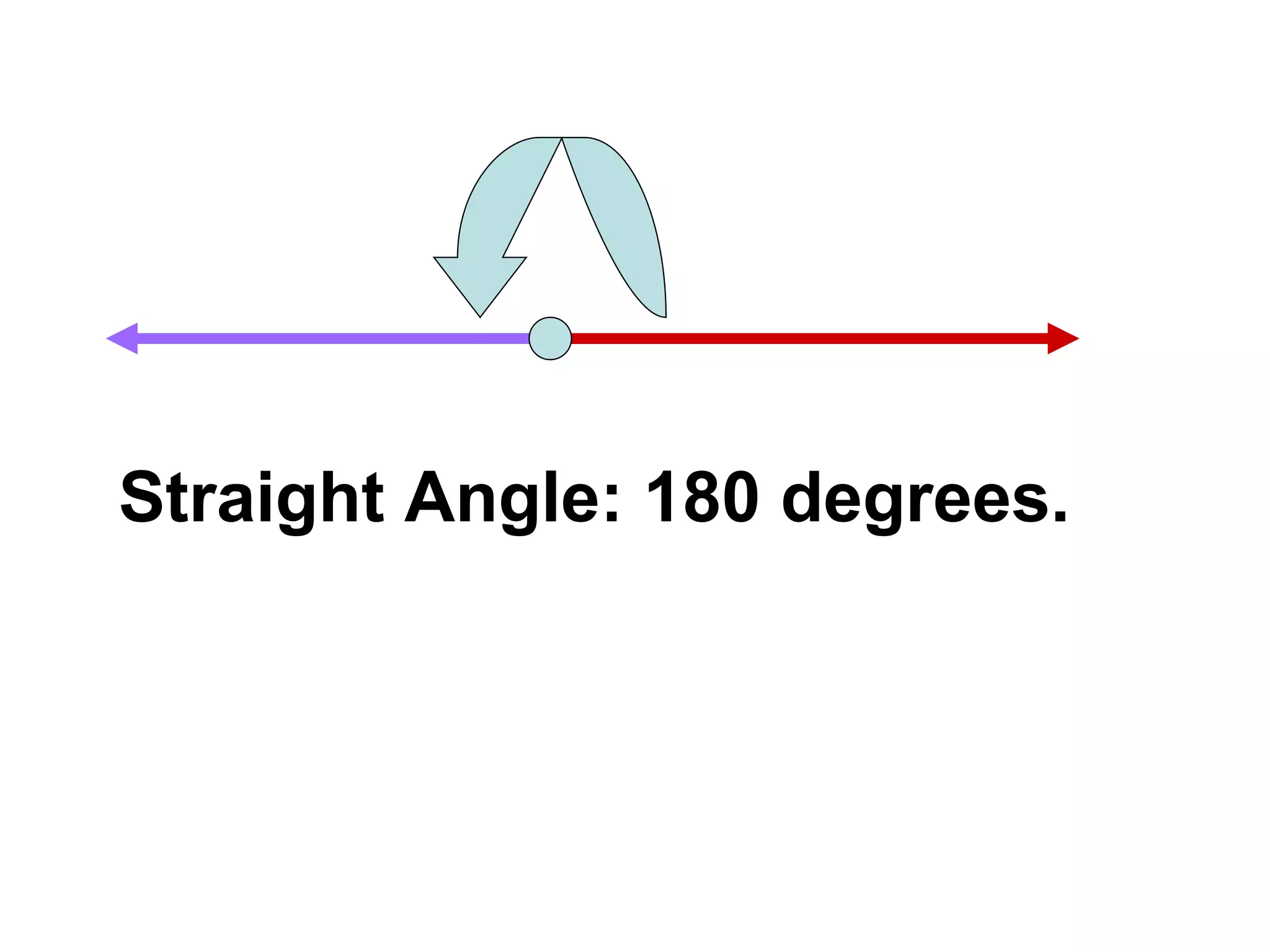
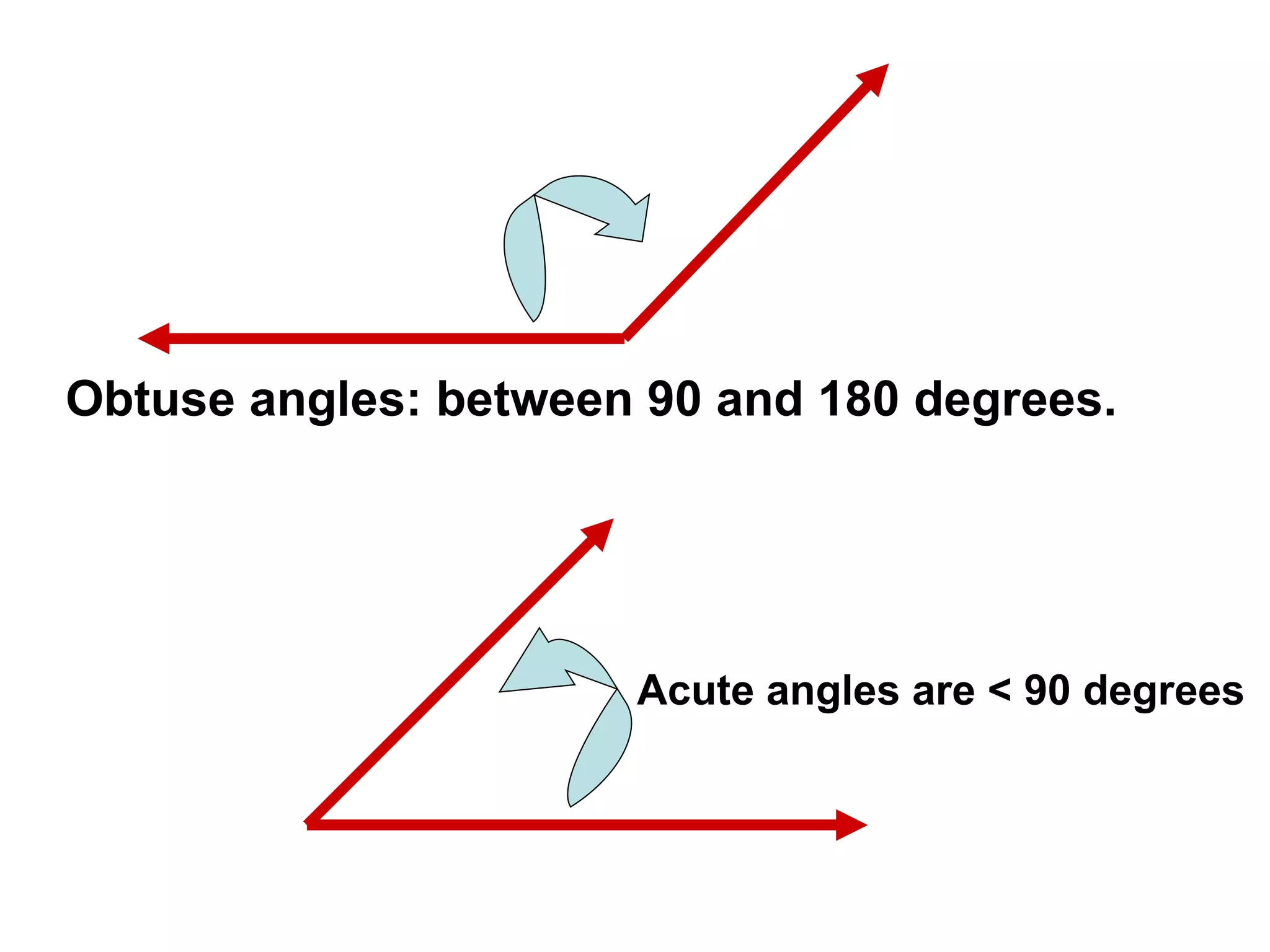
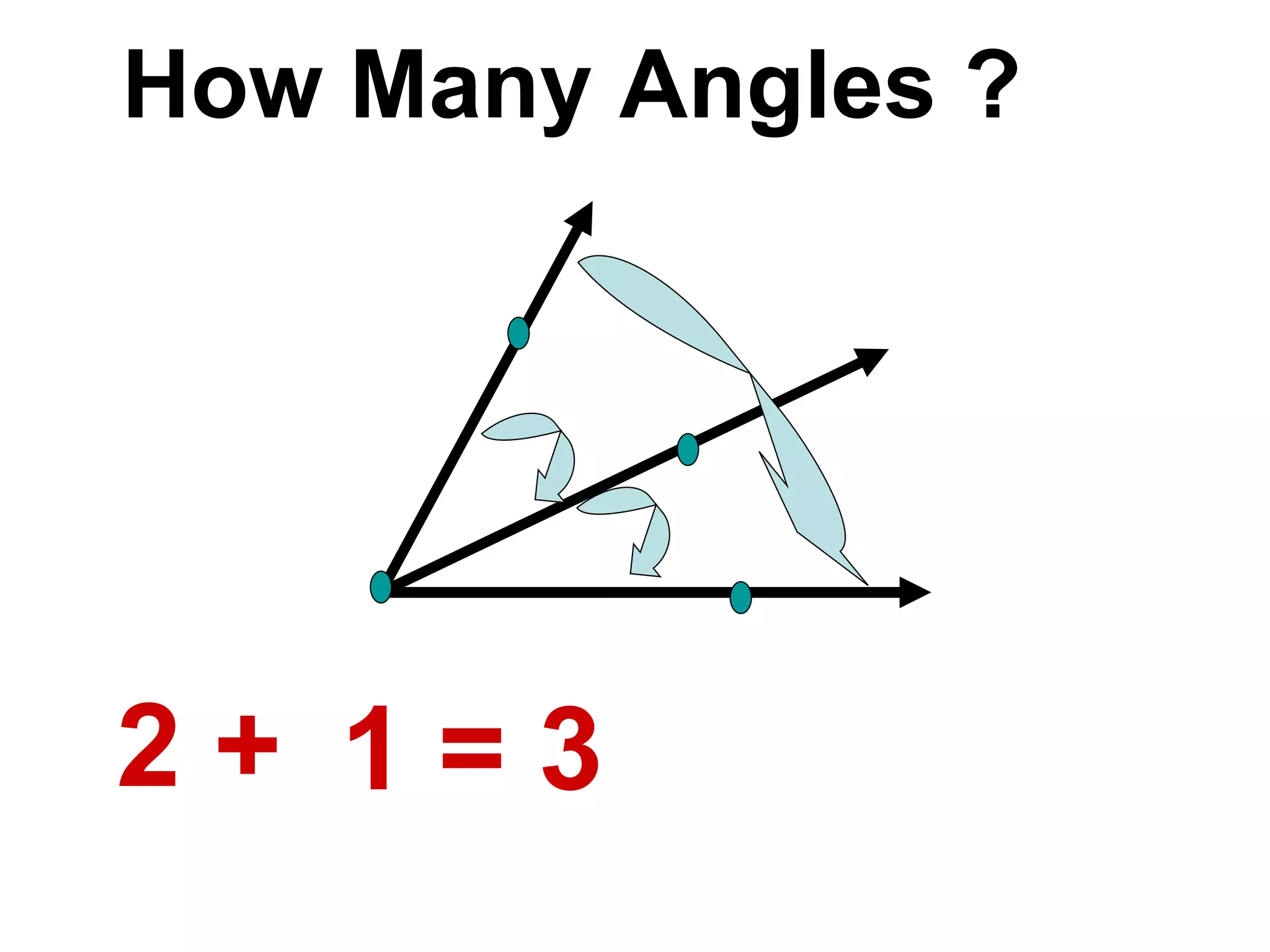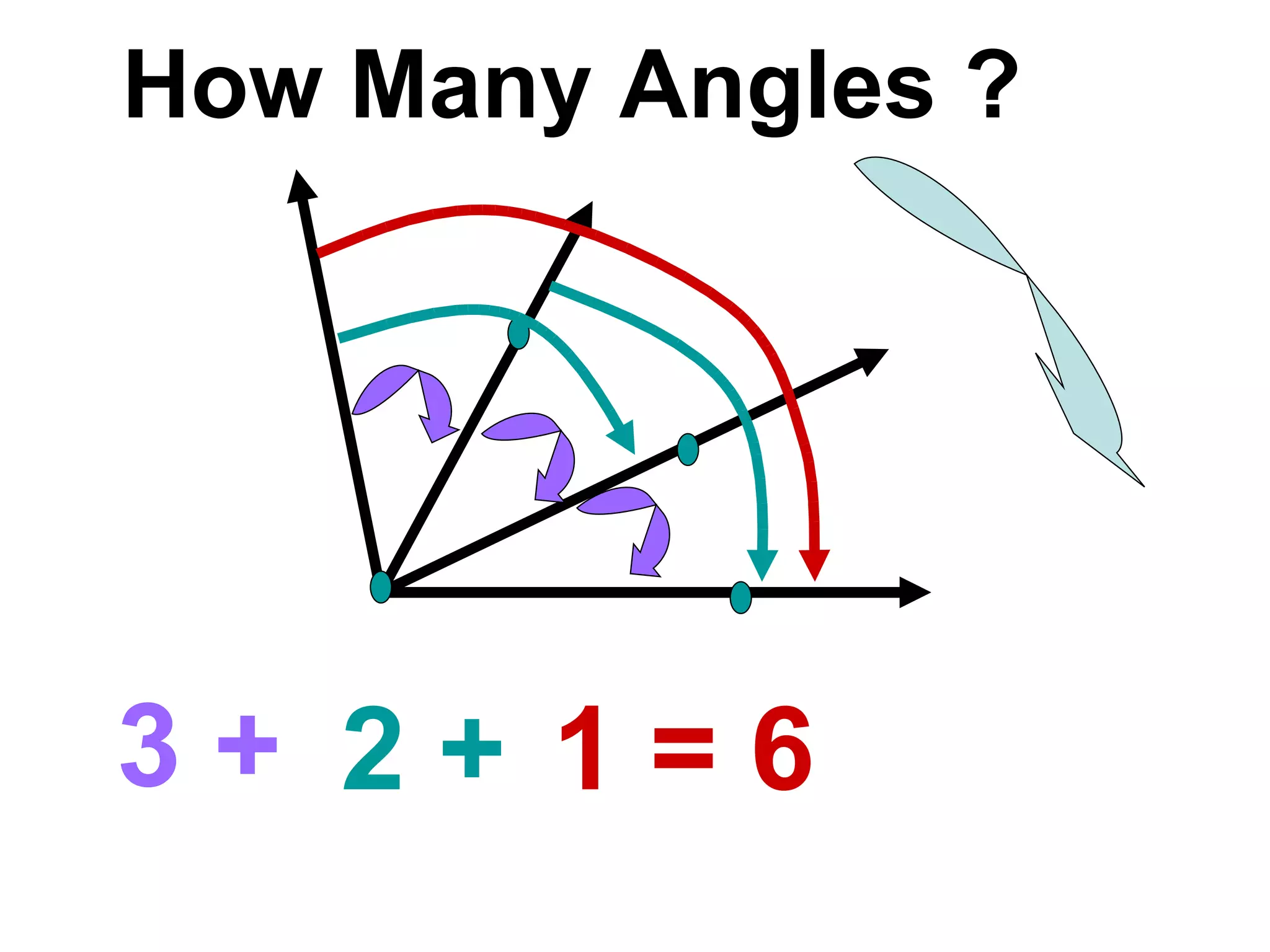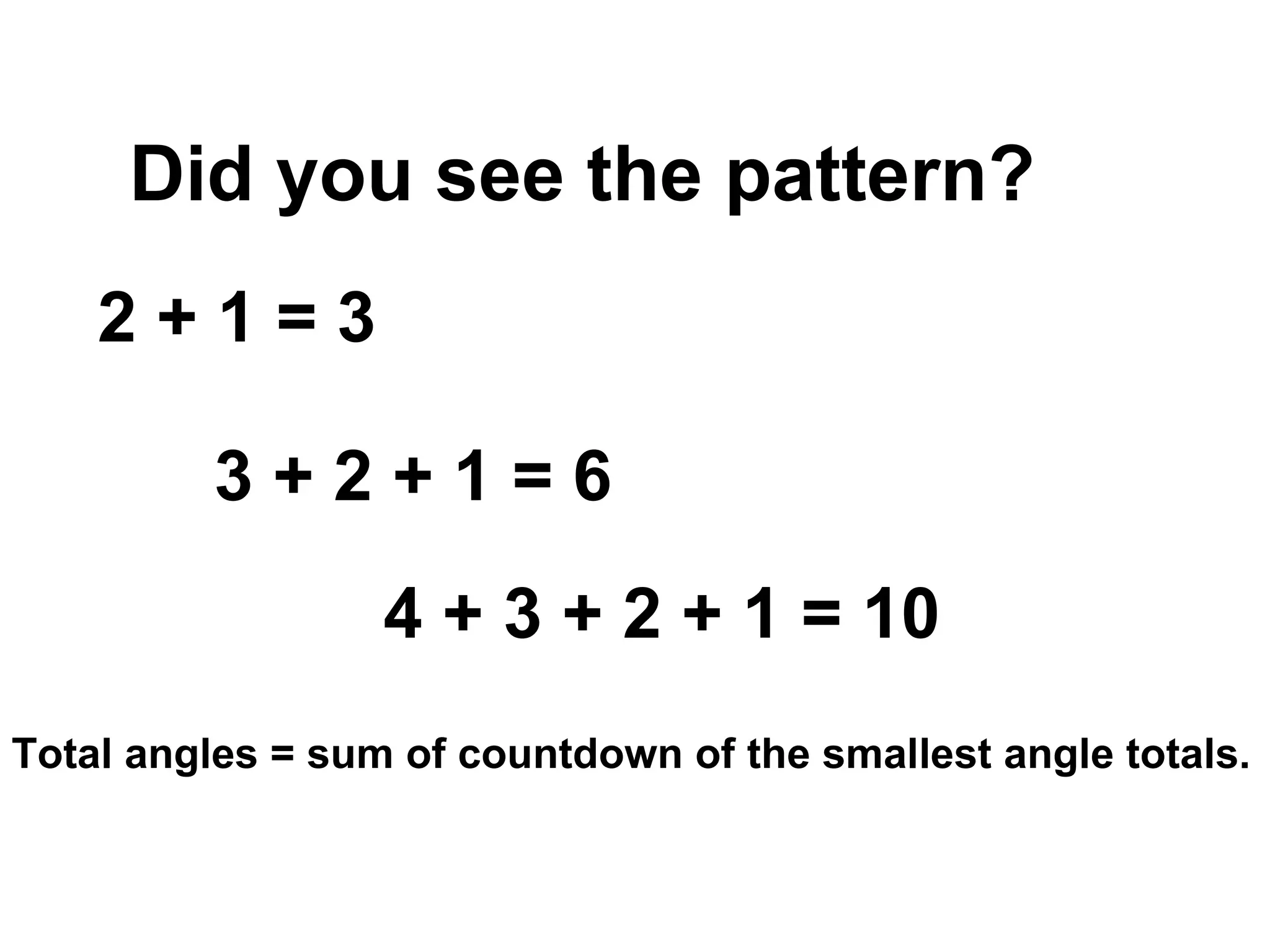There are four types of angles defined by the amount of rotation between two rays sharing an endpoint: acute angles are less than 90 degrees; right angles are 90 degrees; obtuse angles are between 90 and 180 degrees; and straight angles are 180 degrees. Angles are measured using a protractor, which pairs angles with numbers from 0 to 180 degrees. The protractor postulate establishes this measurement method, and the angle addition postulate states that the sum of two adjacent angles is equal to the non-overlapping angle formed.

1. Angles Two rays with a common endpoint. Vertex Side 1 Side 2

2. Model Item Notation An angle is Two rays with a common end point. The parts are the sides ( rays ) , the vertex ( common point), interior space, and exterior space.

3. Angles are classified by rotation of the rays.

4. Zero degrees 90 degrees

5. Straight Angle: 180 degrees.

6. Obtuse angles: between 90 and 180 degrees. Acute angles are < 90 degrees

7. Types of Angles Acute angles are less than 90 degrees Right angles are equal to 90 degrees . [ Looks like letter L ] Obtuse angles are greater than 90 degrees but less than 180 degrees. Straight angles look like lines and are equal to 180 degrees.

8. Types of Angles Angles are differentiated by the quantify of rotation of the rays as if they were hands of a clock. No rotation is zero degrees and totally straight is 180 degrees. 45 degrees 90 degrees

9. Types of Angles Smallest Largest Large Middle Small Zero Acute Right Obtuse Straight

10. Measuring Angles The Protractor

11. Measuring Angles The Protractor Notice, the numbers add up to 180. The smaller number is for the acute angles and the larger number is for the obtuse angles.

12. 50 0

13. 140 0 40 0

14. 35 0 25 0 60 0 60 0

15. 35 0 35 0 57 0 53 0

16. Adjacent Angles 1 2 Same vertex, Common ray, and no common interior

17. Non-Adjacent Angles 1 2 Not the same endpoint.

18. A B T G Non-Adjacent Angles Overlapping Interiors is not allowed.

19. 1 2 3 4 5 6 7 8 9

20. How Many Angles ? 2 + 1 = 3

21. How Many Angles ? 3 + 2 + 1 = 6

22. How Many Angles ? 4 + 3 + 2 + 1 = 10

23. Did you see the pattern? Total angles = sum of countdown of the smallest angle totals. 2 + 1 = 3 3 + 2 + 1 = 6 4 + 3 + 2 + 1 = 10

24. 50 0 Vertex Position One ray must be horizontal. Reading a protractor

25. Protractor Postulate For on a given plane, choose any point O between A and B. Consider and and all the rays that can be drawn from O on one side of . A O B

26. Protractor Postulate These rays can be paired with the real numbers from 0 to 180 in such a way that: A O B is paired with 0 and with 180 . 0 180

27. Protractor Postulate If is paired with x and is paired with y, These rays can be paired with the real numbers from 0 to 180 in such a way that: A O B 0 180 X Y P Q then

28. Protractor Postulate If is paired with x and is paired with y, These rays can be paired with the real numbers from 0 to 180 in such a way that: A O B 0 180 100 150 P Q then Example = 50

29. Example 2 70 120 A C T 50 0 50 0 Top Scale Bottom Scale

30. Angle Addition Postulate If point B lies in the interior of then O C B A And

31. Angle Addition Postulate If is a straight angle and B is any point not on then O C B A

32. Note: The angle addition postulate is just like the segment addition postulate. When the two angles form a straight line then they are called linear pairs . Euclid referred to this concept as … “ The sum of the parts equals the whole.”

33. Angle Addition Applications A B C O 31 0 22 0 53 0

34. Example 2 A B C O 4x +1 22 0 Find the values of the angles. 5x +13 4x +1 +22 = 5x +13 4x +23 = 5x +13 10 = x Substitute back into expressions.

35. Summary There are 4 types of angles: Angles are 2 rays with a common end point. Acute – less than 90 0 Right = 90 0 Obtuse – between 90 0 and 180 0 Straight = 180 0

36. Summary 2 Angles are measured with a protractor. Angles can be indicated by numbers, the vertex, or by 3 letter of which the middle letter is the vertex. The Protractor Postulate establishes measuring angles with a protractor. The Angle Addition Postulate establishes the sum of two adjacent angles is indeed the sum of the two angles.

37. C’est fini. Good day and good luck.