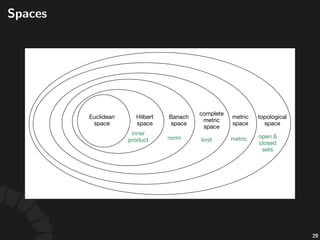
The document is a lecture outline on mathematical concepts crucial for machine learning, covering topics such as topology, metrics, functional analysis, and modern probability theory. It discusses the properties of metrics, open and closed sets, convergence in metric spaces, and various forms of continuity in functions. The material further explores norms, Banach spaces, inner products, and the significance of these structures in the context of machine learning and vector spaces.

1. Lecture'1
Maths&for&Machine&Learning
Dahua%Lin
The$Chinese$University$of$Hong$Kong
1

2. Roadmap
Mathema'cs!lies!at!the!heart!of!machine!learning!
research.!
Complete(coverage(of(all(these(subjects(is(obviously(
beyond(the(scope(of(this(course.(This(lecture(aims(to(give(
an(overview(of(several(useful(math(concepts.
2

3. Concepts)to)Be)Covered
• Basics'of'topology
• metrics
• open'and'closed-sets
• con.nuous-func.on
• compact-space
3

4. Concepts)to)Be)Covered)(cont'd)
• Basics'of'func,onal'analysis
• norm,'inner'product
• Banach'space,'Hilbert'space
• func5onal,'operator
• bilinear'form
4

5. Concepts)to)Be)Covered)(cont'd)
• Basics'of'modern'probability'theory:'
• measure'space
• Lebesgue'integra0on
• random'variables
• expecta0on
• convergence'of'laws
5

6. Metrics
Measurement*of*distances*or*devia*on*lies*at*the*
heart*of*many*learning*problems.*
6

7. Metrics((Defini-on)
• "is"called"a"metric,"if"it"sa-sfies:
• (non*nega-vity)"
• (coincidence2axiom)"
• (symmetry)"
• (triangle2inequality)"
7

8. Metrics((Proper-es)
• The%triangle)inequality%can%be%further%generalized:
!
• A#set# #together#with#a#metric# #defined#thereon#is#
called#a#metric'space,#denoted#by# .
8

9. Examples)of)Metrics
• Euclidean*metric:
• Rec$linear*metric:
!
9

10. Metrics(Induced(by(Transform
• One%can%define%a%metric%over%an%arbitrary%set%$S$%
through%an%injec&ve(map% %to%a%metric%
space% :
• It$can$be$easily$verified$that$ $is$a$metric$on$ .
10

11. Topology'Defined'by'Metrics
• Topological)space"is"a"more"general"concept"than"
metric)space
• With"metrics,"topological)concepts"can"be"defined"
in"a"more"intui7ve"way
11

12. Interior
• Open%ball"of"radius" :"
• "is"an"interior'point"of" "iff" ."
• The"interior"of" ,"denoted"by" "or" ,"is"the"
set"of"all"interior"points"of" .
12

13. Boundary
• "is"a"boundary)point"of" ,"iff"for"any" ," "
overlaps"with"both" "and" ."
• The"boundary"of" ,"denoted"by" ,"is"the"set"of"
all"boundary)points"of" .
13

14. Open%and%Closed%Sets
• Consider*a*metric*space* ,*and*a*subset*
:
• *is*called*an*open%set,*if*
• *is*called*a*closed%set,*if* *is*open
• *is*open*iff* .
• *is*closed*iff* .
14

15. Proper&es(of(Open(and(Closed(Sets
• The%union%of%arbitrary%collec-ons%of%open%sets%is%
open.
• The%intersec-on%of%finitely+many%open%sets%is%open.%
• The%intersec-on%of%arbitrary%collec-ons%of%closed%
sets%is%closed.
• The%union%of%finitely+many%closed%sets%is%closed.
15

16. Ques%ons
• Consider*an*arbitrary*metric*space* ,*are* *and*
*open*or*closed?
• Let* *be*a*finite*metric*space*and* ,*is* *
open*or*closed?
• Consider*Euclidean*space* *and* ,*
is* *open*or*closed?*what*is* ?
16

17. Closure
Let$ $be$a$subset$of$a$metric$space$ :
• The%closure%of% ,%denoted%by% %or% ,%is%defined%
to%be%the%intersec3on%of%all%closed%sets%that%contain%
.
• %is%closed%if%and%only%if% .
• .%
• .
17

18. Closure((Examples)
• .
• .
18

19. Convergence
• Let% %be%a%sequence%in%a%metric%space%
,%then% %is%called%a%limit%of%this%sequence%
if
• A#sequence#is#said#to#be#convergent#if#it#has#a#limit.
• The#limit#of#a#convergent#sequence#is#unique.
19

20. Cauchy'Sequence
• A#sequence# #is#called#a#Cauchy'sequence#if#
!
• A#convergent)sequence#must#be#a#Cauchy)sequence
• Ques%on:#Is#a#Cauchy)sequence#always#convergent?
20

21. Mo#va#ng(Example
• Consider*a*real*valued*sequence*
• We$have$learned$in$Calculus$that$ $as$
.
• Note$that$ $is$a$ra5onal$sequence.$Is$this$
sequence$convergent$in$the$ra#onal'space$ ?
21

22. Complete(Metric(Space
• Convergence)is)not)an)intrinsic)property)of)a)sequence,)
which)also)depends)on)the)space)in)which)the)
sequence)lies.
• A#metric#space# #is#called#a#complete)metric)
space#if#every)Cauchy)sequence)converges.
• #is#complete,#but# #is#not.
• #can#be#constructed#by#comple:ng# .
• Ques%on:#Is#the#integer#space# #complete?#
22

23. Closedness(and(Completeness
Let$ $be$a$subset$of$a$complete$metric$space$ :
• Being'closed'means'"containing-all-the-limits":
• Let' 'be'a'sequence'in' 'and' ,'then'
• 'is'closed'if'and'only'if' 'is'complete,'meaning'all-
convergent-sequences-in- -converge-within- .'
23

24. Bounded
• The%diameter%of% ,%denoted%by% ,%is%defined%to%
be%the%largest%distance%between%points%in% ,%as
• "is"said"to"be"bounded"if" .
24

25. Compactness
• In$elementary$Calculus,$we$learned$that$"every&
bounded&sequence&in& &has&a&convergent&
subsequence".$
• Does$this$hold$in$general$metric$spaces?
25

26. Compactness+(cont'd)
Consider)a)metric)space) :
• "is"called"compact"iff"either"of"the"following"holds:
• Any"open"cover"of" "has"a"finite"subcover.
• "is"complete"and"totally*bounded,"namely,"for"
every" ,"there"is"a"finite"cover"of" "by" >balls.
• "is"sequen1ally*compact,"namely,"every"
sequence"in" "has"a"convergent"subsequence.
26

27. Compactness+(cont'd)
• Compact)sets)are)always)closed'and'bounded.
• But,)the)converse)is)generally'false.
• )is)compact)if'and'only'if) )is)bounded)
and)closed.
27

28. Con$nuous'Func$on
• "is"called"con$nuous,"iff"either"of"the"
following"holds:"
• (Topological)" "is"
open"whenever" "is"open.
• (Weierstrass)"Given"any" "and" ,"
• (Sequen$al3con$nuity)" "whenever"
.
28

29. Con$nui$es)of)Various)Levels
• "is"called"uniformly*con,nuous,"if"
• "is"called"Lipschitz)con,nuous,"if"
!
• Lipschitz)con,nuous" "Uniform)con,nuous" "
Con,nuous."
29

30. Con$nuous'Funcs'on'Compact'Set
• Let% %be%a%con+nuous%func+on,%then%
%is%compact%whenever% %is%
compact.
• Let% ,%then% %assumes%maximum%and%
minimum%within% %when% %is%compact.
• A%con)nuous+func)on%is%uniformly+con)nuous%over%a%
compact%domain.%A%con)nuously+differen)able+
func)on%is%Lipschitz+con)nuous%over%a%compact%
domain.
30

31. Dense%Sets
• A#subset# #is#said#to#be#dense%in% ,#if# .
• A#subset# #is#dense%in% ,#iff#either#of#the#following#
holds:
• Each#open#subset#of# #contains#at#least#one#
element#in# .
• Each# #is#a#limit#of#some#sequence#in# .
• #is#dense#in# ,# #is#dense#in# .
31

32. Separable(Space
• "is"called"a"separable(space,"if" "contains"a"
countable"dense"subset.
• Let" "be"a"con3nuous"func3on"on" ,"and" "is"
dense,"then" "is"uniquely"determined"by" .
• Ques%on:"Let" "be"con3nuous,"and"it"has"
"and" ."
• Is" "determined"by"these"condi3ons?"If"so,"what"
is" ?"
32

33. Things'become'much'more'
interes0ng'when'vector'spaces'meet'
with'metrics.
33

34. Norms
• Consider*a*vector'space* ,*a*func0on* *
is*called*a*norm*if:
•
• *iff* *
• .
• .
34

35. Banach&Spaces
• A#vector#space#together#with#a#norm,#as# ,#
is#called#a#normed'space.#
• A#normed'space#is#always#a#metric'space,#where#
the#norm#induces#a#metric#as# .
• A#complete'normed'space#is#called#a#Banach'space.
35

36. Proper&es(of(Norms
• The%norm%func*on% %is%Lipschitz%
con*nuous:
• The%metric% %induced%by%the%norm%has:
• transla'on)invariance:%
•
36

37. !Norm
Consider)a)real)vector)space) .)For)each) ,)we)
can)define) 6norm)as:
It#can#be#easily#verified#that# #is#a#norm.#
37

38. !Norm
When% ,% 'norm%is%s-ll%a%norm,%defined%as
We#will#extend#these#norms#to#the#space&of&func+ons.
38

39. Convergence)of)Vector)Sequences
• Let% %be%a%sequence%of%vectors%in%a%Banach%
space,%we%say% %converges%to% %if% %
as% .
• This%is%some9mes%called%convergence+in+norm.
39

40. Convergence)of)Series
• Consider*an*infinite*series* *
• Let* .*The*series* *is*said*to*be*
convergent*if*the*sequence* *converges.
• *is*said*to*be*absolutely1convergent*if*the*series*
*converges.
• Absolute1convergence*implies*convergence1(in1norm).
40

41. Basis
• In$elementary$linear$algebra,$we$learned$that$a$basis$
of$a$vector$space$is$a$linearly*independent$set$of$
vectors$that$spans$the$space.
• If$a$vector$space$has$a$finite$basis,$it$is$called$finite/
dimensional.$
• The$cardinali<es$of$all$bases$of$a$finite/
dimensional$space$are$the$same,$called$the$
dimension$of$the$space.
41

42. Basis%of%Banach%Space
• Let% %be%a%sequence%in%a%Banach%space% ,%it%is%
called%a%(Schauder)+basis%of% %if%for%each% ,%
there%exists%a%unique%sequence%of%real%values% %
such%that%
!
• A#Banach#space# #with#a#Schauder#basis#must#be#
separable.
• Is#the#converse#true?#
42

43. Basis%of%Banach%Space%(cont'd)
• It$took$about$forty$years$to$get$the$answer$33$No.$
• Enflo$constructed$a$separable$Banach$space$with$
no$Schauder$basis$in$1973.
43

44. Inner%Products
• An$inner$product$on$a$real$vector$space$ $is$a$
mapping$ $that$sa5sfies:
•
• $iff$
• (symmetry)$
• (bilinearity)$
44

45. Hilbert(Spaces
• A#vector#space#together#with#an#inner#product#is#
called#an#inner%product%space.
• An#inner%product%space#is#always#a#normed%space,#
where#the#norm#is#induced#by#the#inner%product,#as#
.
• A#complete%inner%product%space#is#called#a#Hilbert%
space.
• A#Hilbert%space#is#always#a#Banach%space.
45

46. Euclidean*Space
• "is"a"Hilbert(space"with"the"inner"product"defined"
by" ,"which"induces"the" 5norm"
and"Euclidean(metric.
46

47. Proper&es(of(Inner(Products
• (Parallelogram*equality)"
"##"this"only"
holds"for"norms"induced"by"inner"products.
• (Cauchy–Schwarz*inequality)" ,"or"
equivalently," .
• (Con9nuity)"if" "and" ,"then"
.
47

48. Orthogonality
• "are"said"to"be"orthogonal"to"each"other,"
denoted"by" ,"if" .
• A"subset" "is"called"an"orthogonal)set"if"
elements"of" "are"mutually"orthogonal."Moreover,"
if"each"element"has"a"unit"norm,"then" "is"called"
an"orthonormal)set.
• (Pythagorean)theorem)"
.
48

49. Projec'on
• Let% %and% ,%then%the%distance%between% %
and% %is%defined%to%be% .
• Let% %be%a%non2empty%convex%closed%subset%of% .%
Then%there%exists%a%unique%element% %such%that%
.%This%element% %is%called%the%
projec/on%of% %onto% ,%denoted%by% .
• Ques%on:%Why%does% %need%to%be%closed%and%
convex?
49

50. Projec'on)(cont'd)
Let$ $be$a$Hilbert$space$and$ $be$a$closed$subspace:
• Given' 'and' ,'then' ,'
meaning'that' .
Let$ $be$a$projec,on,$where$ $is$non3empty:
•
• "is"idempotent,"namely," ,"i.e."
.
50

51. Orthogonal*Complement
• A#vector#space# #is#called#the#direct'sum#of#two#
subspaces# #and# ,#denoted#by# ,#if#each#
#can#be#expressed#uniquely#as# #with#
#and# .#
• The#orthogonal'complement#of# ,#denoted#by#
,#is#defined#to#be# .#
• #is#a#closed#subspace#of# .
• ,# .
51

52. Orthonormal*Basis*of*Hilbert*Space
• Let% %be%a%Hilbert%space,%a%subset% %is%called%a%
total%subset%of% %if% %is%dense.
• %is%a%total%subset%of% %if%and%only%if%
.
• Ques%on:%Why%do%we%only%require% %to%
be%dense%instead%of% ?
• A%total%orthonormal%set%is%called%an%orthonormal%
basis.
52

53. Orthonormal*Basis*of*Hilbert*Space
• (Parseval)theorem)"An"orthonormal"sequence" "is"
total"if"and"only"if
• In$this$case,$each$ $can$be$uniquely$expressed$
as$
53

54. Orthonormal*Basis*of*Hilbert*Space*
(cont'd)
• Every'Hilbert'space'has'a'total%orthonormal%set.'
• Every'separable'Hilbert'space'has'a'total%
orthonormal%sequence.
54

55. Spaces
55

56. Linear'Operators'and'Func1onals
• Let% %and% %be%two%linear%spaces,%a%func5on:%
%is%called%a%linear'operator%if%it%preserves%
linear'dependency,%that%is,%
• In$par(cular,$when$ $is$ ,$ $is$called$a$linear'
func+onal.
• The$set$ $is$a$subspace$of$
,$called$the$null'space$of$ .
56

57. Bounded'Operators
Let$ $be$a$linear$operator$on$Banach$spaces:
• "is"said"to"be"bounded,"if"
.
• The"(operator)-norm"of" "is"defined"as
!
• "always"holds.
57

58. Bounded'Operators'(cont'd)
• Given'a'linear'operator' ,'the'following'statements'
are'equivalent:
• 'is'bounded
• 'is'con;nuous
• 'is'finite'
• All'linear'operators'with'finite'dimensional'domain'
are'bounded.
58

59. Space&of&Bounded&Operators
• All$bounded$operators$ $form$a$normed)
space,$denoted$by$ .$
• When$ $is$a$Banach$space,$ $is$a$Banach$
space.
59

60. Dual%Spaces
• All$bounded$func)onals$ $form$a$normed)
space,$called$the$dual)space$of$ ,$denoted$by$ ,$
where$the$norm$is$called$the$dual)norm,$defined$as:
• "is"always"a"Banach"space,"no"ma2er"whether" "
is"or"not.
• "is"generally"not"isomorphic"to"the" .
60

61. Func%on'Space'and'Uniform'Norm
• The%set%of%all%con$nuous%real%valued%func2ons%
defined%on%a%compact+space% %forms%a%normed%
vector%space,%denoted%by% ,%where%the%norm%is%
defined%by% ,%which%is%called%the%
uniform+norm%(or%Chebyshev+norm).
• When% %is%compact,% %is%a%Banach+space.
• There%are%other%ways%to%define%norms%of%func2ons,%
which%we%will%discuss%later.
61

62. Ques%ons
• Let% %be%a%subspace%of% %that%
comprises%all%con$nuously)differen$able)func$ons%on%
.%Let% .%We%define%a%func8onal%as%
%which%takes%the%deriva8ve%at% .%
• Is% %a%linear%func8onal?
• Is% %bounded?
62

63. Representa)on+of+Func)onals
• Every'Hilbert'space'is'isomorphic'to'its'dual%space.
• (Riesz's%theorem)'Every'bounded'linear'func8onal' '
on'a'Hilbert'space' 'can'be'represented'in'terms'of'
inner'product,'namely,' ,'where' 'is'
uniquely'determined'by' 'and'has' .'
• Ques%on:'How'can'you'find' 'given' ?
63

64. Representa)on+of+Func)onals+
(cont'd)
• In$a$separable$Hilbert$space,$ $can$be$expressed$as$
a$series:
64

65. Measure'Theory
• Measure'theory"studies"assigning'values'to'subsets.
• Measure"theory"is"the"corner"stone"of"many"math"
subjects
• Modern"approach"to"integra8on"is"based"on"
measure"theory.
• Modern"probability"theory"is"based"en8rely"on"
measure"theory.
65

66. Lengths(of(Real(Subsets
• Intui'vely,-the-measure-of-a-set-can-be-intepreted-
as-the-size,-e.g.-the-length-of-an-interval.
• How-long-are-these-subsets:- ,- ,-and- ?
• What-is-the-length-of- ?
• Now-let's-try-to-compute-the-length-of- -by-
decomposing0it0into0infinitely0many0points:
66

67. Lengths(of(Real(Subsets((cont'd)
• Sizes'(e.g.'lengths,'areas,'and'volumes)'are'countably-
addi0ve.
• Let' 'be'a'collec;on'of'subsets'of' ,'then'a'
func;on' 'is'said'to'be'countably-addi0ve,'
if'for'any'finite'or'countable'sequence'of'disjoint'
subsets' ,'it'has
67

68. The$Vitali$Set
• Let's'consider'a'very'interes1ng'subset'of' ,'
called'Vitali&set:
• We'say' 'and' 'are'equivalent,'if' .
• 'can'then'be'par11oned'into'mul1ple'
equivalent'classes.
• We'have'incountably&infinite'such'classes
• By'axiom&of&choices,'we'can'form'a'set' ,'which'
contains'one'representa1ve'from'each'class.
68

69. The$length$of$Vitali$Set
• Enumerate*all*ra,onal*numbers*within* *as*
,*and*let* .*Obviously,*
*are*disjoint
• Let* ,*then* ,*and*
therefore* .
• However,*if* ,*then* ,*or*if*
,*then* *...
69

70. Ring%of%Sets
• ,#a#nonempty#collec.on#of#subsets#of# ,#is#called#a#
ring,#if#it#is#closed#under#union#and#set*difference.
• A#ring#must#contain# .
• A#ring#is#closed#under#intersec.on.
• Overall,#we#have:
70

71. !algebra
• A#ring# #is#called#a#algebra,#if#it#is#also#closed#under#
complement.
• An#algebra#must#contain# .
• An#algebra#is#called#a# 5algebra,#if#it#is#also#closed#
under#countable.union.
• A# 5algebra#is#closed#under#countable#fold#of#any#
elementary#set#opera9ons.
71

72. Measure'and'Measure'Space
• A#countably#addi/ve#func/on# #from#a# 5algebra# #
into# #is#called#a#measure.#
• The#triple# #is#called#a#measure'space.#All#the#
elements#of# #are#called#measurable'sets.
72

73. Proper&es(of(Measures
Consider)a)measure'space) :
• .
• .
• Let& &be&disjoint,&then&
.
73

74. Con$nuity)of)Measures
.
.
74

75. Finite&and& )finite&Measures
• "is"called"a"finite&measure"if" .
• "is"called"a" ,finite&measure"if" "is"covered"by"
countably"many"subsets"of"finite"measure.
75

76. Lengths(of(Open(Intervals
• The%length%of%an%open%interval%is%defined%as%
.
• The%the%length%of%a%finite%union%of%disjoint%open%
intervals%is%defined%to%be%the%sum%of%the%lengths%of%
individual%intervals.
76

77. Lengths(of(Open(Intervals((cont'd)
• The%collec)on%of%all%finite%unions%of%disjoint%open%
intervals%cons)tutes%a%ring.
• The%length%is%well%defined%over%this%ring,%and%it%
sa)sfies%finite%addi)vity.%
• Hence,%it%is%called%a%pre'measure.
• We%want%to%extend%the%length%to%as%many%subsets%
as%possible.
77

78. Generated( )algebra
• Let% %be%a%collec+on%of%subsets.%Then%the%smallest%
4algebra%that%contains% %is%called%the% !algebra(
generated(by( ,%denoted%by%
• ,%
• countable%intersec+on%of%unions%of%sets%in% %are%
in% .
78

79. Borel& 'algebra
• Let% %be%a%metric'space.%The% +algebra%generated%by%
the%open%subsets%of% %is%called%the%Borel' .algebra%
of% ,%denoted%by%
• Elements%of%the%Borel% +algebra%are%called%Borel'
sets.
• All%the%open%sets,%closed%sets,%and%their%finite%and%
countable%unions%and%intersec?ons%are%all%Borel'
sets.
• Finite%or%countable%sets%are%all%Borel'sets.
79

80. Measure'Extension
• (Hahn–Kolmogorov.theorem):"Let" "be"a"ring"that"
covers" ," "be"a"pre4measure,"then" "
can"be"extended"to"a"measure" ."If"
"is" 9finite,"then"the"extension"is"unique.
• The"length"func>on"over"the"open"interval"ring"can"
be"uniquely.extended"to"a"measure"over"the"Borel" 9
algebra"over" ,"called"Borel.measure.
80

81. Complete(Measure(Space
We#are#not#done#yet.#Given#a#measure#space#
:
• A#subset# #is#called#a#null$set#if#it#is#contained#
in#a#measurable#set#of#zero#measure.
• This#measure$space#is#called#a#complete$measure$
space#if#every#null#set#is#measurable.
• Let# #denote#the#collec:on#of#all#the#null$sets.#
Then# #is#complete.#
81

82. Lebesgue'Measure
• The%Borel&measure&space%is%generally%not%complete.%
• The%comple.on%of%the%Borel&measure&space%is%called%
the%Lebesgue&measure&space,%and%the%extended%
measure%is%called%Lebesgue&measure.
82

83. Lebesgue'Integral'.'Indicator'
Func4ons
To#derive#the#Lebesgue'integral,#we#begin#with#simple#
func7ons#and#then#extend#the#defini7on#to#more#
general#func7ons.#Let# #be#a#measure#space:
• Indicator+func.ons+00+the+integral+of+an+indicator+
func.on+ +of+a+measurable+set+ +is+defined+to+
be+the+measure+of+ ,+as
83

84. Lebesgue'Integral'.'Simple'Func5ons
• Simple(func-ons(00(linear(combina-ons(of(indicator(
func-ons:
84

85. Lebesgue'Integral'.'Nonnega1ve'
Func1ons
• Let% %be%a%non#nega've%func,on%on% ,%then%we%
define
85

86. Lebesgue'Integral'.'Signed'Func4ons
• Signed(func,on:(decompose( (as( ,(
with( (and( ,(then
• When&both& &and& &are&infinite,&
&is&undefined.
86

87. Proper&es(of(Lebesgue(Integral
• "is"a"linear"func-onal.
• If" "then" "
• a"predicate"holds"almost'everywhere"means"that"it"
holds"over" ,"except"for"a"null"set.
• (Monotonicity)" .
87

88. Monotone&Convergence&Theorem
Let$ $be$a$sequence$of$non#nega've$func.ons,$and$
$pointwisely,$then$
88

89. Dominated*Convergence*Theorem
If# #pointwisely,# #is#dominated#by# ,#i.e.#
,#and# ,#then#
89

90. Integral)with)Coun0ng)Measure
• The%coun%ng'measure%over%a%finite%or%countable%
space% %is%defined%as%the%cardinality%of%subsets.%
• Let% %be%a%coun%ng'measure%over%a%countable%space%
,%then%
!
90

91. Integral)with)Lebesgue)Measure
• Let% %be%a%func,on%over% ,%then%when% %is%
Riemann'integrable,% %must%be%Lebesgue'integrable%
(w.r.t.%the%Lebesgue'measure),%and%in%such%a%case,%the%
Lebesgue'integral%is%equal%to%the%Riemann'integral.%
• Ques%on:%Consider% :
• Is%it%Riemann'integrable?
• Compute%the%Lebesgue'integral%of% %with%respect%
to%the%Lebesgue'measure.
91

92. !space
• For%any% ,%the% %space%of% ,%denoted%by%
,%is%the%vector%space%comprised%of%all%
measurable%func8ons%on% %such%that%
,%where%the% )norm%is%defined%by
• Ques%on:"Is"it"actually"a"norm?
92

93. !space!(cont'd)
• Func&ons)that)are)equal)almost'everywhere)are)
indis&nguishable)by)integra&on.)Let) )denotes)
the)vector)space)with)all)essen/ally'equivalent)
func&ons)merged)into)an)element.)
• Then) )is)a)Banach'space)with)the) >norm.
• The) )norm)is)defined)as)the)essen/al'supreme)of)
,)as
93

94. !Space!and!Dual
• The%dual%space%of% %is%isomorphic%to% %with%
.%
• For%each%bounded%func8onal%on% ,%there%
exists% :%
94

95. !Hilbert!Space
• "is"a"Hilbert"space,"where"the"inner"product"is"
defined"as
• The%dual%space%of% %is% .
95

96. Absolute)Con,nuity
Let$ $and$ $be$two$measures$over$ :
• "is"said"to"be"absolutely*con-nuous"with"respect"to"
,"denoted"by" ,"if" "whenever"
.
• "and" "are"said"to"be"singular,"denoted"by" ,"if"
there"exists" "such"that" "and"
.
96

97. Lebesgue'Decomposi.on
Let$ $and$ $be$two$measures$over$ :
There%exists%a%unique%decomposi3on%of% %as%
!
such%that% %and% .
97

98. Radon&Nikodym,Theorem
Let$ $be$a$finite$measure$that$is$absolutely*con-nuous$
with$respect$to$ .$Then$there$exists$an$essen-ally$
unique$ :$
Here,% %is%called%the%Radon&Nikodym,density%of% %with%
respect%to% .%In%this%case,%we%also%have
98

99. Event&Spaces
• The% &algebra% %can%be%interpreted%as%an%event%
space.%Each%element% %is%an%event.
• % %both% %and% %happen
• % %either% %or% %happens
• % % %does%not%happen
• % % %and% %are%mutually%exclusive.
99

100. Probability*Measure
• A#probability*measure# #is#a#measure#on# #with#
.
• #can#be#considered#as#the#probability#of#the#
event# .
• Obviously,# #sa:sfies#all#the#requirement#of#
probability#func:ons#in#classical#probability#theory.
100

101. Independence
• Two%events% %and% %are%said%to%be%independent%if%
• We$say$two$collec-ons$of$events$ $and$ $are$
independent$when$
101

102. Random'Variables
• A#(real&valued)+random+variable# #is#defined#to#be#a#
measurable+func4on# .
• Each#random#variable# #induces#a#sub7 7algebra,#
denoted#by# ,#where# #is#the#Borel# 7algebra#
of# .
• Two#random#variables# #and# #are#said#to#be#
independent#if# #and# #are#
independent.
102

103. Expecta(on
• The%expecta'on%of%a%random%variable% %is%defined%
to%be
!
• The%expecta'on%is%a%bounded-linear-func'onal.
103

104. Probability*and*Law
• The%probability%that%the%value%of% %falling%in% %is%
then%given%by%
."
• The%func*on% ,%which%maps%each%Borel%set%
%to%a%probability*value,%is%itself%a%probability*
measure%over% ,%which%is%called%the%law%of% ,%
denoted%by% .
104

105. Probability*Density
• The%Radon+Nikodym%density%of% %with%respect%
to%the%Lebesgue%measure%over% ,%denoted%by% ,%is%
called%the%probability*density%of% .%So%we%have%
.
105

106. (Seman'c)*Correspondence
• "algebra) )event)space
• sub" "algebra) )a)family)of)events
• measure) ) )probability)func6on
• measurable)func6on) ) )random)variable
• ) )law)of)
• integra6on) )expecta6on
• Radon"Nikodym)density) )probability)density
106

107. Convex'Analysis
• Convex(op*miza*on(plays(a(crucial(role(in(many(
machine(learning(problems
• Prof.(Stephen'Boyd(has(a(very(famous(book("Convex'
Op1miza1on",(which(provides(an(excellent(
treatment(of(this(subject
• The(PDF(version(is(available(for(download(in(
Prof.(Boyd's(website
• You(should(at(least(read(the(first(five(chapters
107

108. Convex'Analysis'(cont'd)
• Important*concepts
• convex'set
• convex'func,on
• conjugate'func,on
• Lagrange'dual
• strong'duality'and'weak'duality
• We*will*begin*to*use*these*concepts*in*Lecture*3.
108