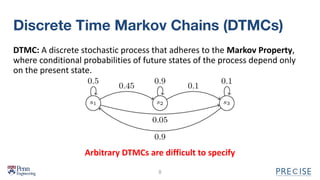
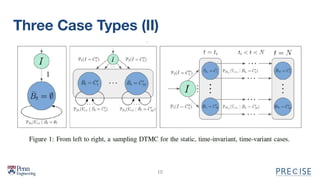
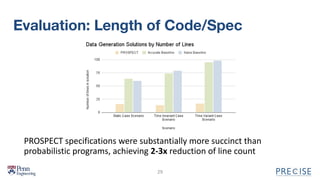
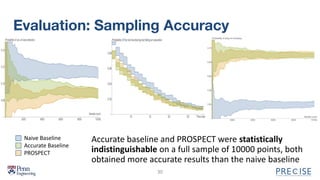
The document describes PROSPECT, a tool for automatically generating synthetic data from probabilistic specifications. PROSPECT allows users to specify discrete temporal distributions declaratively and solves the specifications algebraically to obtain unique parameter solutions. If a unique distribution is defined, PROSPECT can sample from it. The document outlines PROSPECT's specification language and approach, which involves parameterizing specifications, solving systems of equations, and sampling solutions. An evaluation found PROSPECT specifications were more succinct than probabilistic programs and generated accurate data.

1. Data Generation with
PROSPECT: A Probability
Specification Tool
Alan Ismaiel, Ivan Ruchkin, Jason Shu, Oleg Sokolsky, Insup
Lee
University of Pennsylvania Computer and Information Science Department
Winter Simulation Conference 2021
December 14th, 2021
1

2. Motivating Scenario: Autonomous Car
• Engineering team is building autonomous cleaning vehicle
• Team intends to simulate the vehicle in desired conditions:
• Time of day is determined by the cleaning schedule
• Lane occupancy is determined by the parking ticket history
• Obstacle detection rate differs by time of day
2
How should they simulate the conditions?

3. Motivating Scenario: Network Latency
• Network monitor estimates latency based on N latest ping delays
• Need simple synthetic data to test the monitor
• Goal: quickly generate a simple dataset of
• Observed ping delays
• Underlying network latencies
• Desirable properties of the dataset:
• Low latency on average
• Ping delays change occasionally over time
• High latency sometimes leads to high ping delays
3
How to generate this dataset?

4. Automated Data Generation
• Increasingly important: testing complex systems, deep learning
• Obtaining real data often infeasible or impractical
• Many information sources: requirements, common-sense constraints,
intuition, known statistics
Current data generation tools:
• Tailored to specific model
• Imperative sampling
• Little support for arbitrary constraints
• High complexity
4

5. Problem
Declaratively specify and automatically sample discrete temporal distribution
under known constraints:
● Algebraic constraints on marginal/joint/conditional probabilities
● Conditional/unconditional independence
● Temporal relations
5
Intractable in general

6. Approach Overview
1) Define tractable cases with a shared underlying model
2) The user specifies a distribution in our high-level declarative language
3) The specification is translated into polynomial equations
4) The system of polynomial equations is solved algebraically
5) If the solution defines a unique distribution, we sample it
6

7. Approach Overview
1) Define tractable cases with a shared underlying model
2) The user specifies a distribution in our high-level declarative language
3) The specification is translated into polynomial equations
4) The system of polynomial equations is solved algebraically
5) If the solution defines a unique distribution, we sample it
7

8. Discrete Time Markov Chains (DTMCs)
DTMC: A discrete stochastic process that adheres to the Markov Property,
where conditional probabilities of future states of the process depend only
on the present state.
8
Arbitrary DTMCs are difficult to specify

9. Three Case Types (I)
Static Case: Time is irrelevant, sampling is conducted i.i.d.
Time-Invariant Case: Sampling is not independent, but the temporal
distributions don’t change over time.
Time-Variant Case: Sampling is not independent, and the temporal
distributions change over time.
9

10. Three Case Types (II)
10

11. Approach Overview
1) Define tractable cases with a shared underlying model
2) The user specifies a distribution in our high-level declarative language
3) The specification is translated into polynomial equations
4) The system of polynomial equations is solved algebraically
5) If the solution defines a unique distribution, we sample it
11

12. Specification Language: Scenario
12

13. Specification: Case and Variables
DSL
13

14. Specification: Independence
DSL
14

15. Specification: Probability Constraints
DSL
15

16. Approach Overview
1) Define tractable cases with a shared underlying model
2) The user specifies a distribution in our high-level declarative language
3) The specification is translated into polynomial equations
4) The system of polynomial equations is solved algebraically
5) If the solution defines a unique distribution, we sample it
16

17. Parameterizing Specifications
Goal: Parameterize all the probability specifications into algebraic equations
We define O-Parameters to represent the probabilities of elementary events
over the user’s defined sample space.
Every syntax element can be expressed with O-Parameters:
• Parameterize conditional and unconditional event probabilities
• Parameterize conditional and unconditional independence
• Parameterize the stationary assumption (time invariant case)
• Parameterize recursive probability specifications (time variant case)
17

18. Motivating Scenario Parameters (1)
18

19. Motivating Scenario Parameters (2)
19

20. Motivating Scenario Parameters (3)
20

21. Approach Overview
1) Define tractable cases with a shared underlying model
2) The user specifies a distribution in our high-level declarative language
3) The specification is translated into polynomial equations
4) The system of polynomial equations is solved algebraically
5) If the solution defines a unique distribution, we sample it
21

22. Solving a System of Equations
Goal: Find unique distribution parameters satisfying the equations in step 3
Relies on Buchberger’s Algorithm and Cylindrical Algebraic Decomposition,
solving algorithms that are guaranteed to terminate.
Our implementation based on Wolfram Mathematica automatically picks an
appropriate solving algorithm, and returns solutions in complex numbers
22
• We only consider solutions that define valid probability distributions

23. Solving for Unique Solutions
Solving algorithm returns a set S of probability distributions.
● |S|= 1: the distribution is unique
● |S| > 1: the distribution is underspecified (not enough constraints for a
unique distribution)
● |S|< 1: the distribution is overspecified (conflicting constraints, no
distribution possible)
23

24. Solving the Motivating Scenario
24

25. Approach Overview
1) Define tractable cases with a shared underlying model
2) The user specifies a distribution in our high-level declarative language
3) The specification is translated into polynomial equations
4) The system of polynomial equations is solved algebraically
5) If the solution defines a unique distribution, we sample it
25

26. PROSPECT
PROSPECT is a software tool that allows users to provide an input made in
the specification language, and outputs generated data.
https://prospect.precise.seas.upenn.edu
https://github.com/bisc/prospect
26

27. PROSPECT (Pre-Recorded Demo)
27

28. Evaluation
Goal: Compare the required manual effort, length of code/specification, and
accuracy of data generation between PROSPECT approach and probabilistic
programming (PPL) baseline
For each scenario, we made two data generation programs in the PPL Pyro
v1.5.1:
1. Accurate solution, correctly interprets specifications and assumptions,
manually inferring the intended distribution
2. Naive solution, demonstrates plausible errors by ignoring implicit
dependencies between variables
28

29. Evaluation: Length of Code/Spec
29
PROSPECT specifications were substantially more succinct than
probabilistic programs, achieving 2-3x reduction of line count

30. Evaluation: Sampling Accuracy
30
Naive Baseline
Accurate Baseline
PROSPECT
Accurate baseline and PROSPECT were statistically
indistinguishable on a full sample of 10000 points, both
obtained more accurate results than the naive baseline

31. Future Work
• Syntax extensions for broader sampling settings:
• Continuous parametric distributions
• Probabilities constrained by variable values
• Semantic extensions for under-specified distributions:
• Resolving ambiguity with meta-models
• Tuning to available data
• Tool extensions for usability:
• Conditional termination of sampling
• When over-specified, return the minimal conflicting sub-spec
31

32. Conclusion
Our contributions:
1. A specification language for discrete distributions
2. An algebraic inference approach for distributions from the specifications
3. A software tool PROSPECT that implements the language and interface
4. An evaluation of PROSPECT on 3 case studies
We believe this approach can be used for simulation, probabilistic reasoning,
design and analysis, and other tasks that require probabilistic specifications.
https://prospect.precise.seas.upenn.edu
32

33. Related Works
DSLs: SESSL, NEDL, build deterministic designs with predefined patterns
• PROSPECT samples potentially complex random designs, compliments the work
Simulators: CARLA, Udacity, X-Plane, AirSim
• Focuses on specific discrete domains whereas PROSPECT performs at any level of abstraction
Graphical Models: Markov/Bayesian Networks
• PROSPECT represents a domain-agnostic approach that can create graphical models
PPLs: Pyro, Scenic
• Stronger focus on inferring a model given a program and dataset, whereas PROSPECT relies on explicit
declarative specifications
Coupla: ARTA, NORTA, VARTA, Stochastic Programming: SAMPL
• Focus on continuous distributions, not discrete, requires knowledge/data to choose models, PROSPECT does
not
33