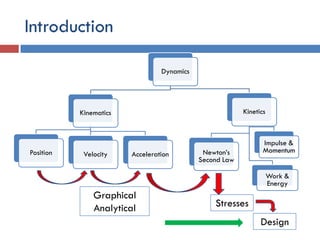
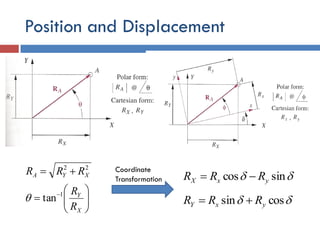
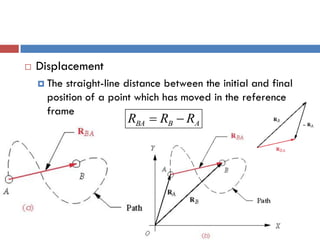
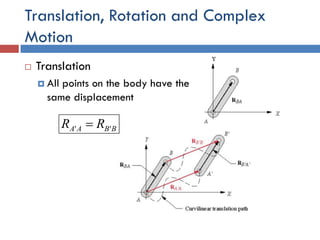
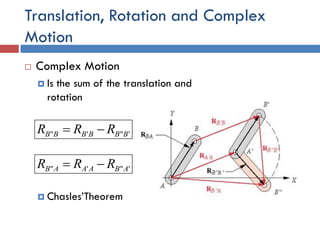
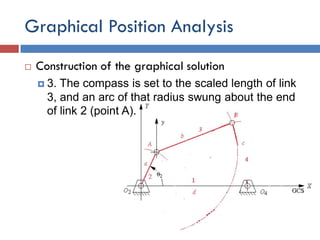
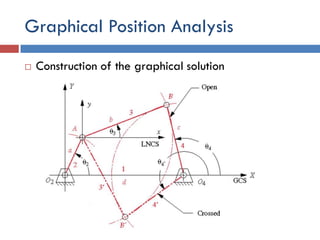
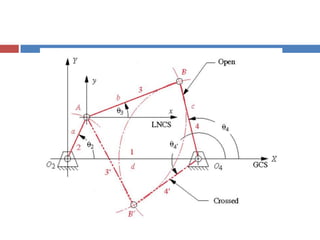
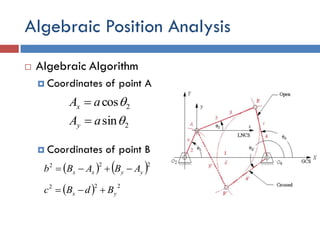
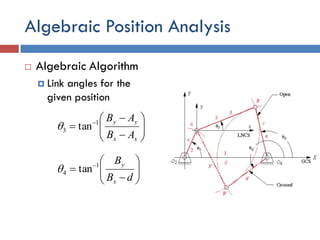
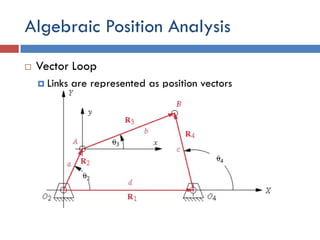
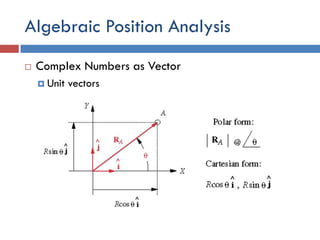
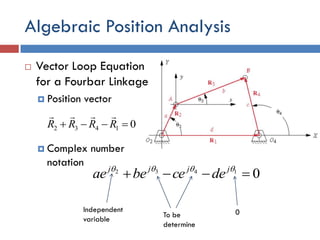
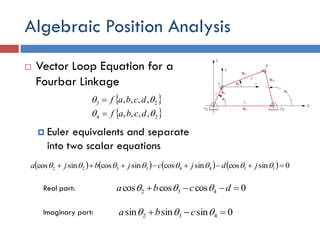
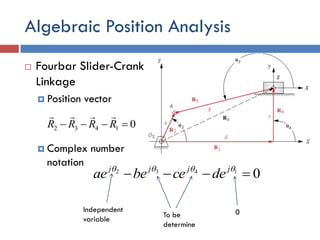
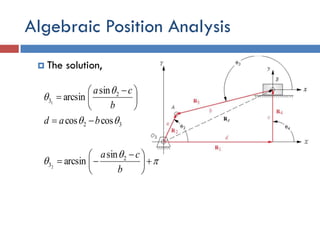
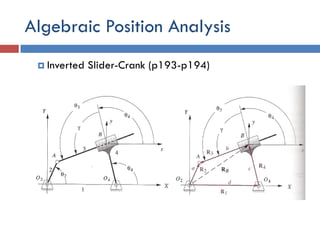
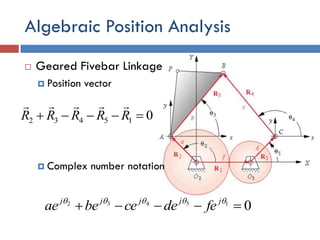
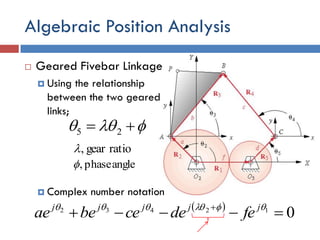
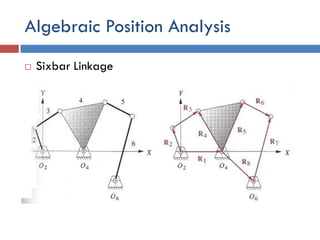
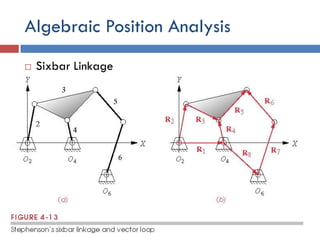
This document provides an overview of position analysis techniques for linkages and mechanisms. It discusses coordinate systems, position and displacement concepts, and methods for graphical and algebraic position analysis. Graphical methods involve drawing the linkage to scale based on given parameters and measuring positions. Algebraic methods develop vector loop equations in terms of complex numbers and solve for unknown positions and angles. Specific techniques are presented for common linkages including fourbars, slider-cranks, and geared fivebars.

1. POSITION ANALYSIS
Chapter 4

2. Introduction
Dynamics
Kinematics
Position Velocity Acceleration
Kinetics
Newton’s
Second Law
Work &
Energy
Impulse &
Momentum
Stresses
Design
Graphical
Analytical

3. Coordinate Systems
 Global or Absolute
 Attached to Earth
 Local
 Attached to a link at some point
of interest
 LNCS (local nonrotating
coordinate system)
 LRCS (local rotating coordinate
system)

4. Position and Displacement
22
XYA RRR 






 
X
Y
R
R1
tan
Coordinate
Transformation  sincos yxX RRR 
 cossin yxY RRR 

5.  Displacement
 The straight-line distance between the initial and final
position of a point which has moved in the reference
frame
ABBA RRR 

6. Translation, Rotation and Complex
Motion
 Translation
 All points on the body have the
same displacement
BBAA RR '' 

7. Translation, Rotation and Complex
Motion
 Rotation
 Different points in the body
undergo different
displacements and thus there is
a displacement difference
between any two points chosen
 Euler’s theorem
BAABBB RRR  ''

8. Translation, Rotation and Complex
Motion
 Complex Motion
 Is the sum of the translation and
rotation
 Chasles’Theorem
'"'" BBBBBB RRR 
'"'" ABAAAB RRR 

9. Graphical Position Analysis
 For any one-DOF, such a fourbar, only one
parameter is needed to completely define the
positions of all the links. The parameter usually
chosen is the angle of the input link.

10. Graphical Position Analysis
 Construction of the graphical solution
 The a, b, c, d and the angle θ2 of the input link are
given.
 1. The ground link (1) and the input link (2) are
drawn to a convenient scale such that they
intersect at the origin O2 of the global XY
coordinate system with link 2 placed at the input
angle θ2.
 2. Link 1 is drawn along the X axis for
convenience.

11. Graphical Position Analysis
 Construction of the graphical solution

12. Graphical Position Analysis
 Construction of the graphical solution
 3. The compass is set to the scaled length of link
3, and an arc of that radius swung about the end
of link 2 (point A).

13. Graphical Position Analysis
 Construction of the graphical solution
 4. Set the compass to the scaled length of link 4,
and a second arc swung about the end of link 1
(point O4). These two arcs will have two
intersections at B and B’ that define the two
solution to the position problem for a fourbar
linkage which can be assembled in two
configurations, called circuits, labeled open and
crossed.
 5. The angles of links 3 and 4 can be measured
with a protractor.

14. Graphical Position Analysis
 Construction of the graphical solution

16. Algebraic Position Analysis
 Algebraic Algorithm
 Coordinates of point A
 Coordinates of point B
2cosaAx 
2sinaAy 
   222
yyxx ABABb 
  222
yx BdBc 

17. Algebraic Position Analysis
 Algebraic Algorithm
 Coordinates of point B
     dA
BA
S
dA
BA
dA
dcba
B
x
yy
x
yy
x
x







2
2
2
2
2
2222
02
2
2







 c
dA
BA
SB
x
yy
y
P
PRQQ
By
2
42


 
12
2



dA
A
P
x
y
 
dA
SdA
Q
x
y



2
  22
cSdR 
 dA
dcba
S
x 


2
2222

18. Algebraic Position Analysis
 Algebraic Algorithm
 Link angles for the
given position








 
xx
yy
AB
AB1
3 tan







 
dB
B
x
y1
4 tan

19. Algebraic Position Analysis
 Vector Loop
 Links are represented as position vectors

20. Algebraic Position Analysis
 Complex Numbers as Vector
 Unit vectors

21. Algebraic Position Analysis
 Complex Numbers as Vector
 Complex number notation

22. Algebraic Position Analysis
 Complex Numbers as Vector
 Complex number notation
 Euler identity

sincos je j




j
j
je
d
de



23. Algebraic Position Analysis
 Vector Loop Equation
for a Fourbar Linkage
 Position vector
 Complex number
notation
01432  RRRR

01432
  jjjj
decebeae
0Independent
variable
To be
determine

24. Algebraic Position Analysis
 Vector Loop Equation for a
Fourbar Linkage
 Euler equivalents and separate
into two scalar equations
 
 24
23
,,,,
,,,,


dcbaf
dcbaf


        0sincossincossincossincos 11443322   jdjcjbja
Real part: 0coscoscos 432  dcba 
0sinsinsin 432   cbaImaginary part:

25. Algebraic Position Analysis
 Solve simultaneously
 Square and add
dcab  423 coscoscos 
423 sinsinsin  cab 
     2
42
2
423
2
3
22
coscossinsincossin dcacab  
   2
42
2
42
2
coscossinsin dcacab  
 424242
2222
coscossinsin2cos2cos2   accdaddcab

26. Algebraic Position Analysis
 To simplify, constants are define in terms of the
constant link length,
 Substituting the identity,
 Freudenstein’s equation
a
d
K 1
424232241 sinsincoscoscoscos   KKK
c
d
K 2
ac
dcba
K
2
2222
3


  424242 sinsincoscoscos  
 4232241 coscoscos   KKK

27. Algebraic Position Analysis
 Using half angle identities,
 Simplified form














2
tan1
2
tan2
sin
42
4
4


















2
tan1
2
tan1
cos
42
42
4



0
2
tan
2
tan 442












CBA

  3221
2
32212
cos1
sin2
coscos
KKKC
B
KKKA







28. Algebraic Position Analysis
 The solution,
 If the solution is complex conjugate, the link lengths
chosen are not capable of connection
 The solution will usually be real and unequal
 Crossed (+)
 Open (-)
A
ACBB
2
4
2
tan
2
4 













 

A
ACBB
2
4
arctan2
2
4 2,1


29. Algebraic Position Analysis
 Solution for θ3
 Square and add
dbac  324 coscoscos 
324 sinsinsin  bac 
323252431 sinsincoscoscoscos   KKK
b
d
K 4
ab
badc
K
2
2222
5


0
2
tan
2
tan 332












FED

  5241
2
52412
cos1
sin2
coscos
KKKF
E
KKKD







30. Algebraic Position Analysis
 The solution,
 If the solution is complex conjugate, the link lengths
chosen are not capable of connection
 The solution will usually be real and unequal
 Crossed (+)
 Open (-)







 

D
DFEE
2
4
arctan2
2
3 2,1


31. Algebraic Position Analysis
 Fourbar Slider-Crank
Linkage
 Position vector
 Complex number
notation
01432  RRRR

01432
  jjjj
decebeae
0Independent
variable
To be
determine

32. Algebraic Position Analysis
 Vector Loop Equation for a
Fourbar Linkage
 Euler equivalents and separate
into two scalar equations
        0sincossincossincossincos 11443322   jdjcjbja
Real part: 0coscoscos 432  dcba 
0sinsinsin 432   cbaImaginary part:

33. Algebraic Position Analysis
 The solution,
32
2
3
coscos
sin
arcsin1



bad
b
ca






 



 




 

b
ca 2
3
sin
arcsin2

34. Algebraic Position Analysis
 Inverted Slider-Crank (p193-p194)

35. Algebraic Position Analysis
 Geared Fivebar Linkage
 Position vector
 Complex number notation
015432  RRRRR

015432
  jjjjj
fedecebeae

36. Algebraic Position Analysis
 Geared Fivebar Linkage
 Using the relationship
between the two geared
links;
 Complex number notation
  25
 
012432
   jjjjj
fedecebeae
ratiogear,
anglephase,

37. Algebraic Position Analysis
 Geared Fivebar Linkage
 Solution (pag. 196)







 

D
DFEE
2
4
arctan2
2
4 2,1

  
  
   
 









22
22
2
22222
22
22
sinsin2
coscos2
cos2
sinsin2
coscos2
ad
fad
affdcbaC
adcB
fadcA
CAF
BE
ACD



2

38. Algebraic Position Analysis
 Geared Fivebar Linkage
 Solution (pag. 196)







 

L
LNMM
2
4
arctan2
2
3 2,1

  
  
   
 









22
22
2
22222
22
22
sinsin2
coscos2
cos2
sinsin2
coscos2
ad
fad
affdcbaK
dabH
fdabG
KGN
HM
GKL



2

39. Algebraic Position Analysis
 Sixbar Linkage

40. Algebraic Position Analysis
 Sixbar Linkage