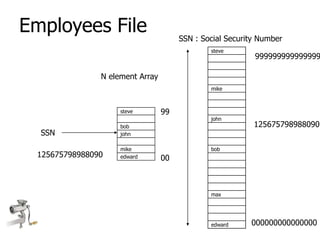
This document describes hash maps and hash tables. It provides examples of using a hash function to map keys to indexes in an array, which can store key-value pairs. It discusses concepts like collisions, load factor, and different strategies for handling collisions like open addressing and closed addressing.

1. HASH MAP

2. Hash
Table
KEY VALUE
Key Value Pair

3. Key VALUE
pierre 01.42.78.96.12
paul 03.67.90.67.00
françois 01.45.87.90.45
mohamed 04.88.8945.29
khaled 06.98.56.22.48
laila 01.23.45.67.89
alex 34.56.15.27.78.
claire 34.56.73.45.67
philippe 02.34.26.48.26.
Hash()
françois 01.45.87.90.45
Phone Numbers list example

4. Key VALUE
pierre 01.42.78.96.12
paul 03.67.90.67.00
françois 01.45.87.90.45
mohamed 04.88.8945.29
khaled 06.98.56.22.48
laila 01.23.45.67.89
alex 34.56.15.27.78.
claire 34.56.73.45.67
philippe 02.34.26.48.26.
Hash()
françois 01.45.87.90.45
Phone Numbers list example
Key Value

5. Employees File SSN : Social Security Number
125675798988090
000000000000000
999999999999999
Social Security Number = address

6. Employees File SSN : Social Security Number
125675798988090
000000000000000
999999999999999
Social Security Number = address
steve
mike
john
bob
max
edward
John SSN : 125675798988090

7. Employees File SSN : Social Security Number
125675798988090
000000000000000
999999999999999
Social Security Number = address
steve
mike
john
bob
max
edward
Requires Memory size :
999999999999999
= 1E+15 = 1 petaoctet (Po)
John SSN : 125675798988090

8. Employees File SSN : Social Security Number
125675798988090
000000000000000
999999999999999
N element Array
SSN
00
99
steve
mike
john
bob
max
edward
125675798988090
100 employees

9. Employees File SSN : Social Security Number
125675798988090
000000000000000
999999999999999
N element Array
SSN
00
99
steve
mike
john
bob
max
edward
steve
bob
john
mike
edward125675798988090

10. Employees File SSN : Social Security Number
125675798988090
000000000000000
999999999999999
N element Array
SSN
00
99
steve
mike
john
bob
max
edward
steve
bob
john
mike
edward125675798988090

11. Employees File SSN : Social Security Number
125675798988090
000000000000000
999999999999999
steve
N element Array
00
99
KEY
hash
bob
john
mike
edward
value
addresses
steve
mike
john
bob
max
edward

12. Hashing
125675798988090000000000000000 999999999999999
00 99

13. Hashing
125675798988090000000000000000 999999999999999
00 99

14. Hashing
125675798988090000000000000000 999999999999999
00 99

15. Hashing

16. Employees File
SSN : Social Security Number
125675798988090
000000000000000
999999999999999
john
N element Array
00
99
KEY
hash
bob
mike
edward
value
addresses
steve
mike
john
bob
max
edward
Key
space
Address
space

17. Key space to Address space
mapping
125675798988090
000000000000000
999999999999999
Address
space
Key
space
00
99

18. Key space to Address space
mapping
125675798988090
000000000000000
999999999999999
Address
space
Key
space
Index
00
99

19. Buckets principle

20. Hash Function
 The hash function is used to transform the key into the
index (the hash) of an array element (the slot or bucket)
where the corresponding value is to be stored and sought.
KEY HASH
index
Value
Bucket (slot)

21. Hash table
 hash table is an array-based data structure.
129007
926647
975378
269908
Fred
Steve
Richard
Robert
Key Value
0
1
3
4
5
2
index
SSN

22. Hash table
 hash function is used to convert the key into
the index of an array element, where
associated value is to be seek.
129007
926647
975378
269908
Fred
Steve
Richard
Robert
Key Value
h(129007)
h(129007)
h(975378)
h(269908)
0
1
3
4
5
2
index
SSN
buckets

23. Collision
 If the hash function returns a slot that is
already occupied there is a collision
129007
975378
269908
Fred
Richard
Robert
Key Value
H(129007)
H(975378)
H(269908)
H(926647)
0
1
3
4
2

24. 0
1
3
4
5
2
hash clustering
 When the distribution of keys into buckets is not random,
we say that the hash table exhibits clustering.
129007
975378
269908
Fred
Richard
Robert
Key Value
H(697803)
H(975378)
H(269908)
H(926647)
H(168477)
H(129007)
6
7

25. Hash function
Good Hash function provides uniform
distribution of hash values.
Poor hash function will cause collisions and
hash cluster.

26. Hash Distribution
Value # Hash
0 2
1 2
2 2
3 2
4 0
5 0
6 0
7 0
8 0
9 0
10 1
0
1
2
3
1 2 3 4 5 6 7 8 9 10 11
# Hash

27. Hash Distribution
0
1
2
1 2 3 4 5 6 7 8 9 10 11
# Hash
# Hash
Value # Hash
0 1
1 1
2 1
3 1
4 1
5 1
6 1
7 1
8 1
9 1
10 1

28. Hash Distribution
Value # Hash
0 0
1 0
2 0
3 1
4 3
5 5
6 3
7 1
8 0
9 0
10 0
0
1
2
3
4
5
6
1 2 3 4 5 6 7 8 9 10 11
# Hash
# Hash

29. Hash function toy implementation :
Modulo N R CAR(R) mod (11)
A 65 10
B 66 0
C 67 1
D 68 2
E 69 3
F 70 4
G 71 5
H 72 6
I 73 7
J 74 8
K 75 9
L 76 10
M 77 0
N 78 1
O 79 2
P 80 3
Q 81 4
R 82 5
S 83 6
T 84 7
U 85 8
V 86 9
W 87 10
X 88 0
Y 89 1
Z 90 2
26 => 11

30. Modulo N Hash Distribution

31. Load Factor
Key Value
0 B 0
1 C 4
2 O 1
3 E 2
4 P 3
5 X 6
6 N 7
7 D 8
8 M 9
9
10 L 5
Key Value
0 B 0
1 C 4
2 O 1
3 E 2
4 P 3
5 X 6
6 N 7
7 D 8
8 M 9
9
10 L S
11
12
13
14
15
16
17
18
19
20
21
# elements in the hash Table
size of the hash table
48 %
91 %

32. Collision handling strategies
Closed addressing (open hashing).
Open addressing (closed hashing).
0
1
3
4
5
2
129007
975378
269908
Fred
Richard
Robert
Key Value
H(697803)
H(975378)
H(269908)
H(926647)
H(168477)
H(129007)
6
7

33. Open addressing (closed hashing).
 When there is a collision, "Probe" the array to
find an empty slot after the occupied slot.
129007
926647
975378
269908
Fred
Steve
Richard
Robert
Key Value
H(697803)
H(975378)
H(269908)
H(926647)
168477 Phil
697803 Greg
H(168477)
H(129007)

34. Closed addressing (open hashing).
Each slot of the hash table contains a link to
another data structure.
129007
926647
975378
269908
Fred
Steve
168477 Phil
697803 Greg
Key
129007
975378 Richard
269908 Robert

35. Linear Hashing
• Linear Hashing
– Re-hash : hi (x) = (h(x) + i) mod B
• Stepsize : i
• i = 1,2,3, …
• Quadratic Hashing
– Re-hash : hi (x) = (h (x) + i ²) mod B
• Stepsize : i2
• i2 = 1,4,9,…
• Double Hashing
– Re-hash : hi (x) = (h(x) + i g (x)) mod B
• Stepsize : g(x)

36. Toy implementation example : R
Attribut ARelation R
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M

37. modulo
Char Ascii Code
Value Key
RID R CAR(R) mod (11)
0 B 66 0
1 O 79 2
2 E 69 3
3 P 80 3
4 C 67 1
5 L 76 10
6 X 88 0
7 N 78 1
8 D 68 2
9 M 77 0

38. Class HashLinearProbing
 Hash(key)  returns hash
 Put (key, value)  inserts key value pair
 Get (key)  gets key value
 Remove (key)  removes key preserving bucket
structure.

39. Class HashMap JSE 1.4
Object get(Object key)
Returns the value to which the specified key is
mapped in this identity hash map, or null if the map
contains no mapping for this key.
Object put(Object key, Object value)
Associates the specified value with the specified key
in this map.
Object remove(Object key)
Removes the mapping for this key from this map if
present

40. Linear Probing toy implementation
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
KEY VAL
0
1
2
3
4
5
6
7
8
9
10
M
N
Relation Data Structure Implementation
Logical
Physical

41. Linear Probing toy implementation
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
KEY VAL
0
1
2
3
4
5
6
7
8
9
10
M
N
M > N
Empty Slot is
Search Stop Condition

42. Linear Probing toy implementation
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
KEY VAL
0
1
2
3
4
5
6
7
8
9
10
11
10
M > N
Empty Slot is
Search Stop Condition

43. Linear Probing
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
X 6
O 1
E 2
P 3
N 7
V 4
L 5
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0
Hash(key)
First
Empty
Slot ?
Put(N,7)
%M
Empty Slot is
Search Place Stop Condition

44. Linear Probing
Hash(key)
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
X 6
O 1
E 2
P 3
N 7
K 8
M 9
V 4
L 5
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0
Car Y = 89
Y mod 11 = 1
Hash(key)
Get(Y)
Y ?
Empty
Stop
Return (-1) Empty Slot is
Search Stop Condition

45. Linear Probing toy implementation
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
KEY VAL
0
1
2
3
4
5
6
7
8
9
10
11
10
M > N
Empty Slot is
Search Stop Condition
At least one empty slot
M – N = 1

46. Linear Probing
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
KEY VAL
0
1
2
3
4
5
6
7
8
9
10
M
N

47. Linear Probing
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
Example Relation
Implementation

48. Linear Probing
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
Hash(key) = CAR(R) Mod (M)
M = 11
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0

49. Linear Probing
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
Hash(key)
Put(B,0)
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0

50. Linear Probing
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
O 1
Hash(key)
Put(O,1)
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0

51. Linear Probing
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
O 1
E 2
Hash(key)
Put(E,2)
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0

52. Linear Probing
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
O 1
E 2
P 3
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0
Hash(key)
First
Empty
Slot ?
Put(P,3)

53. Linear Probing
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
O 1
E 2
P 3
V 4
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0
Hash(key)
Put(V,4)

54. Linear Probing
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
O 1
E 2
P 3
V 4
L 5
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0
Hash(key)
Put(L,5)

55. Linear Probing
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
X 6
O 1
E 2
P 3
V 4
L 5
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0
Hash(key)
First
Empty
Slot ?
Put(X,6)
%M

56. Linear Probing
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
X 6
O 1
E 2
P 3
N 7
V 4
L 5
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0
Hash(key)
First
Empty
Slot ?
Put(N,7)
%M

57. Linear Probing
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0
Hash(key)
First
Empty
Slot ?
Put(K,8)
%M
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
X 6
O 1
E 2
P 3
N 7
K 8
V 4
L 5

58. Linear Probing
Hash(key)
Put(M,9)
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
X 6
O 1
E 2
P 3
N 7
K 8
M 9
V 4
L 5
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
First
Empty
Slot ?
0
2
3
3
9
10
0
1
9
0

59. Linear Probing
Hash(key)
Put(M,9)
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
X 6
O 1
E 2
P 3
N 7
K 8
M 9
V 4
L 5
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0

60. Linear Probing
Hash(key)
Put(M,9)
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
X 6
O 1
E 2
P 3
N 7
K 8
M 9
V 4
L 5
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0

61. Implementation of function Hash(Key)
 In Java : Key % M
 Specific case of Java char : in Java char are integer (Byte).
 char: The char data type is a single 16-bit Unicode character. It has a minimum
value of 'u0000' (or 0) and a maximum value of 'uffff' (or 65,535 inclusive).
 Null char is 0 (zero).
 Default value for char is 0, or u0000.
Hash (Key) { Return Key Modulo M }
http://docs.oracle.com/javase/tutorial/java/nutsandbolts/datatypes.html

62. Bucket Table Implementation
KEY VAL
char keys Array [M] int values Array [M]

63. Put(key, value) simplified algo
M = # bucket entries
index = hash (key)
While Key [index) != empty
index = (index + 1) % M
End while
Key [index] = key
Values [index] = value

64. Get(Key)
 Get existing key
 Get non inserted key

65. Linear Probing
Hash(key)
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
X 6
O 1
E 2
P 3
N 7
K 8
M 9
V 4
L 5
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0
Hash(key)Hash(key)
Get(B)
B,0
B ?

66. Linear Probing
Hash(key)
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
X 6
O 1
E 2
P 3
N 7
K 8
M 9
V 4
L 5
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0
Hash(key)
Get(M)
M ?
M, 9

67. Linear Probing
Hash(key)
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
X 6
O 1
E 2
P 3
N 7
K 8
M 9
V 4
L 5
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0
Hash(key)
K ?
K,8
Get(K)

68. Linear Probing
Hash(key)
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
X 6
O 1
E 2
P 3
N 7
K 8
M 9
V 4
L 5
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0
Car Y = 89
Y mod 11 = 1
Hash(key)
Get(Y)
Y ?
Empty
Stop
Return (-1)

69. Get(key)
M = # buckets
index = hash (key)
valueToReturn = -1 // value to return if the key is not in the map
While Key [index] != key and Key [index] != empty
index = (index + 1) % M
End while
If (Key [index] = key) valueToReturn = Values [index]
Return valueToReturn

70. Remove (Key)
 Remove (M)
 Remove (N) : rehash end of the cluster.
 Remove (L) : rehash end of the cluster.

71. Linear Probing
Hash(key)
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
X 6
O 1
E 2
P 3
N 7
K 8
M 9
V 4
L 5
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0
Hash(key)
Remove (M)
K(0) != M
Blank
Scan for M

72. Linear Probing
Hash(key)
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
X 6
O 1
E 2
P 3
N 7
K 8
V 4
L 5
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0
Hash(key)
Remove (M)
K(0) != M
Blank
Scan for M

73. Linear Probing
Hash(key)
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
X 6
O 1
E 2
P 3
N 7
K 8
M 9
V 4
L 5
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0
Hash(key)
Remove (N)
K(1) != N
Blank and rehash
End of cluster
Scan for N

74. Linear Probing
Hash(key)
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
X 6
O 1
E 2
P 3
N 7
K 8
M 9
V 4
L 5
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0
Cluster
Remove (N)
K(1) != N
Blank and rehash
End of cluster
Scan for N

75. Linear Probing
Hash(key)
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
X 6
O 1
E 2
P 3
K 8
M 9
V 4
L 5
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0
Remove (N)
K(1) != N
Blank and rehash
End of cluster
Scan for N
EOf
cluster

76. Linear Probing
Hash(key)
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
X 6
O 1
E 2
P 3
K 8
M 9
V 4
L 5
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0
Remove (N)
K(1) != N
Blank and rehash
End of cluster
Scan for N
EOf
cluster
Blank Key(6) , Val(6)
put(K,8)

77. Linear Probing
Hash(key)
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
X 6
O 1
E 2
P 3
M 9
V 4
L 5
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0
Remove (N)
K(1) != N
Blank and rehash
End of cluster
Scan for N
EOf
cluster
Blank Key(6) , Val(6)
put(K,8)

78. Linear Probing
Hash(key)
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
X 6
O 1
E 2
P 3
M 9
V 4
L 5
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0
Remove (N)
K(1) != N
Blank and rehash
End of cluster
Scan for N
Blank Key(6) , Val(6)
put(K,8)

79. Linear Probing
Hash(key)
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
X 6
O 1
E 2
P 3
M 9
V 4
L 5
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0
Remove (N)
K(1) != N
Blank and rehash
End of cluster
Scan for N
Blank Key(6), Val(6)
put(K,8)

80. Linear Probing
Hash(key)
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
X 6
O 1
E 2
P 3
K 8
M 9
V 4
L 5
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0
Remove (N)
K(1) != N
Blank and rehash
End of cluster
Scan for N
Blank Key(7) ,Val(7)
put(K,8)

81. Linear Probing
Hash(key)
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
X 6
O 1
E 2
P 3
K 8
M 9
V 4
L 5
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0
Remove (N)
K(1) != N
Blank and rehash
End of cluster
Scan for N
Blank Key(7) ,Val(7)
put(K,8)

82. Linear Probing
Hash(key)
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
X 6
O 1
E 2
P 3
K 8
V 4
L 5
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0
Remove (N)
K(1) != N
Blank and rehash
End of cluster
Scan for N
Blank Key(7) , Val(7)
put(M,9)

83. Linear Probing
Hash(key)
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
X 6
O 1
E 2
P 3
K 8
V 4
L 5
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0
Remove (N)
K(1) != N
Blank and rehash
End of cluster
Scan for N
Blank Key(7) , Val(7)
put(M,9)
First
Empty
Slot ?

84. Linear Probing
Hash(key)
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
X 6
O 1
E 2
P 3
K 8
9
V 4
L 5
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0
Remove (N)
K(1) != N
Blank and rehash
End of cluster
Scan for N
Blank Key(7) , Val(7)
put(M,9)
First
Empty
Slot ?
M

85. Linear Probing
Hash(key)
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
X 6
O 1
E 2
P 3
N 7
K 8
M 9
V 4
L 5
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0
Remove (L)

86. Linear Probing
Hash(key)
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
X 6
O 1
E 2
P 3
N 7
K 8
M 9
V 4
L 5
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0
K(10) = L blank
Remove (L)
Blank and rehash
End of cluster

87. Linear Probing
Hash(key)
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
X 6
O 1
E 2
P 3
N 7
K 8
M 9
V 4
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0
K(10) = L blank
Remove (L)
Blank and rehash
End of cluster

88. Linear Probing
Hash(key)
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
X 6
O 1
E 2
P 3
N 7
K 8
M 9
V 4
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0
K(10) = L blank
Remove (L)
Blank and rehash
End of cluster
EOf
cluster

89. Linear Probing
Hash(key)
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
X 6
O 1
E 2
P 3
N 7
K 8
M 9
V 4
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0
Remove (L)
Blank and rehash
End of cluster
EOf
cluster
Blank Key(0) , Val(0)
put(B,0)

90. Linear Probing
Hash(key)
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
X 6
O 1
E 2
P 3
N 7
K 8
M 9
V 4
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0
Remove (L)
Blank and rehash
End of cluster
EOf
cluster
Blank Key(1) , Val(1)
put(X,6)

91. Linear Probing
Hash(key)
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
X 6
O 1
E 2
P 3
N 7
K 8
M 9
V 4
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0
Remove (L)
Blank and rehash
End of cluster
EOf
cluster
Blank Key(2) , Val(2)
put(O,1)

92. Linear Probing
Hash(key)
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
X 6
O 1
E 2
P 3
N 7
K 8
M 9
V 4
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0
Remove (L)
Blank and rehash
End of cluster
EOf
cluster
Blank Key(3) , Val(3)
put(E,2)

93. Linear Probing
Hash(key)
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
X 6
O 1
E 2
P 3
N 7
K 8
M 9
V 4
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0
Remove (L)
Blank and rehash
End of cluster
EOf
cluster
Blank Key(4), Val(4)
put(P,3)

94. Linear Probing
Hash(key)
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
X 6
O 1
E 2
P 3
N 7
K 8
M 9
V 4
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0
Remove (L)
Blank and rehash
End of cluster
EOf
cluster
Blank Key(5), Val(5)
put(N,7)

95. Linear Probing
Hash(key)
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
X 6
O 1
E 2
P 3
N 7
K 8
M 9
V 4
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0
Remove (L)
Blank and rehash
End of cluster
EOf
cluster
Blank Key(6) , Val(6)
put(K,8)

96. Linear Probing
Hash(key)
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
X 6
O 1
E 2
P 3
N 7
M 9
V 4
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0
Remove (L)
Blank and rehash
End of cluster
EOf
cluster
Blank Key(6) , Val(6)
put(K,8)

97. Linear Probing
Hash(key)
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
X 6
O 1
E 2
P 3
N 7
M 9
V 4
K 8
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0
Remove (L)
Blank and rehash
End of cluster
EOf
cluster
Blank Key(6) , Val(6)
put(K,8)

98. Linear Probing
Hash(key)
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
X 6
O 1
E 2
P 3
N 7
M 9
V 4
K 8
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0
Remove (L)
Blank and rehash
End of cluster
EOf
cluster
Blank Key(7) , Val(7)
put(M,9)

99. Linear Probing
Hash(key)
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
X 6
O 1
E 2
P 3
N 7
M 9
V 4
K 8
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0
Remove (L)
Blank and rehash
End of cluster
EOf
cluster
Blank Key(7) , Val(7)
put(M,9)

100. Linear Probing
Hash(key)
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
X 6
O 1
E 2
P 3
N 7
M 9
V 4
K 8
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0
Remove (L)
Blank and rehash
End of cluster
EOf
cluster
Blank Key(7) , Val(7)
put(M,9)

101. Linear Probing
Hash(key)
KEY VAL
B 00
1
2
3
4
5
6
7
8
9
10
X 6
O 1
E 2
P 3
N 7
M 9
V 4
K 8
Value Key
RID R
0 B
1 O
2 E
3 P
4 V
5 L
6 X
7 N
8 K
9 M
0
2
3
3
9
10
0
1
9
0
Remove (L)
Blank and rehash
End of cluster
EOf
cluster
Blank Key(7) , Val(7)
put(M,9)

102. Remove (key) simplified algo
M = # buckets
index = hash (key)
While Key [index) != key and Key [index) != empty
index = (index + 1) % M
End while
Key [index] = 0, Value [index] = 0
// rehash
index = (index + 1) % M
While Key [index) != empty
savedKey = Key [index], savedValue = Value [index]
Key [index] = 0 Value [index] = 0
Put ( savedKey , savedValue )
index = (index + 1) % M
End while

103. The End