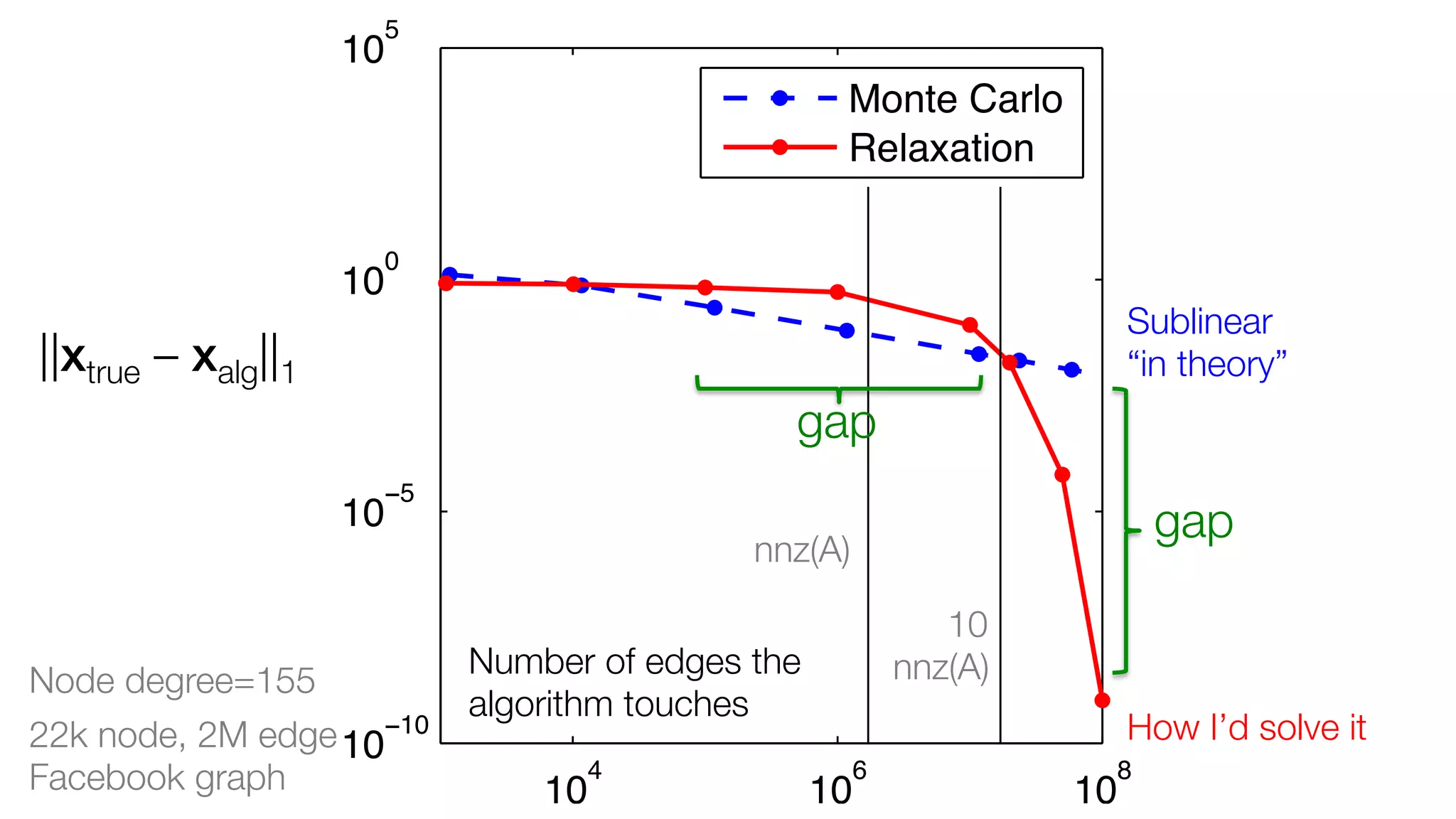
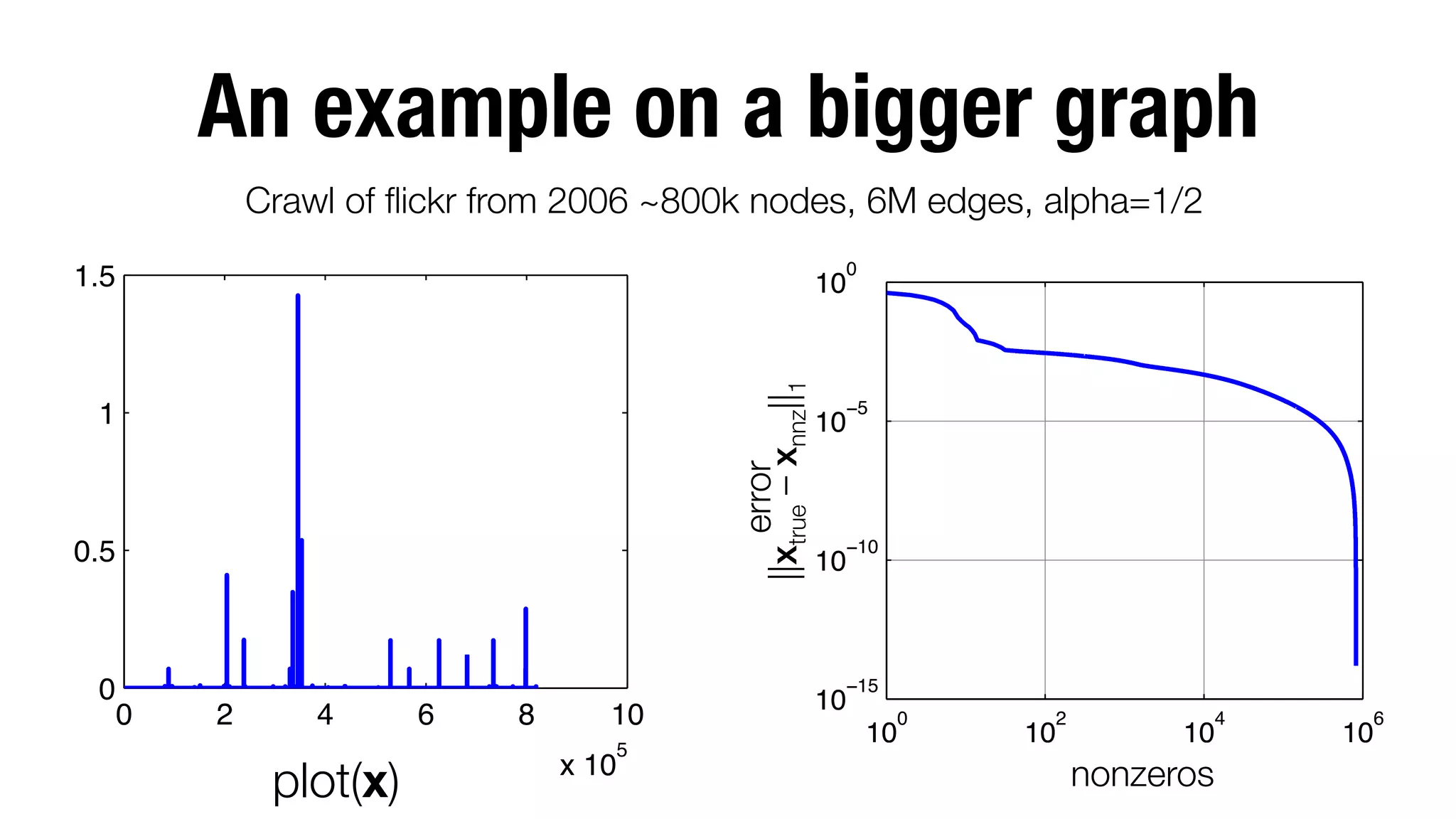
This document discusses gaps between theory and practice in large scale matrix computations for networks. It provides an overview of representing networks as matrices and canonical problems like PageRank that can be modeled as matrix computations. It then discusses different methods for solving these problems, like Monte Carlo methods, relaxation methods, and Krylov subspace methods. It analyzes the computational complexity of these approaches and identifies open problems, such as developing unified convergence results for different algorithms and handling "top k" convergence. The talk concludes by identifying more structured problems on networks that could leverage matrix computations.

1. Gaps between theory
practice in !
!
!
large scale matrix computations for networks
David F. Gleich
Assistant Professor
Computer Science
Purdue University

2. Networks as matrices
Bott, Genetic Psychology Manuscripts, 1928

3. Networks as matrices

4. Networks as matrices

5. Networks as matrices
A =

6. Everything in the world can be
explained by a matrix, and we see
how deep the rabbit hole goes
The talk ends, you
believe -- whatever
you want to.
Image from rockysprings, deviantart, CC share-alike
6

8. Matrix computations in a red-pill
Solve a problem better by
exploiting its structure!

9. My research!
Models and algorithms for high performance !
A
L
B
Tensormatrix and network computations on data
eigenvalues"
This proposal is for matchand a power method
ing triangles using
Network alignment
tensor Massive matrix "
CH, Y. HOU, AND J. TEMPLETON
P
methods:
maximize
Tijk xi xj xk
-
j0
Triangle
j
i
k
k
0
i0
std
2
A
L
ijk
computations
subject to kxk2 = 1
AxX b
=
[x(next) ]i = ⇢ · (
j xk
min kAx Tijk xbk+
jk
where ! ensures the 2-norm
Ax = x
SSHOPM method due to "
B
Fast & Scalable"
Network analysis
xi )
Kolda and Mayo
on multi-threaded
IfHuman,proteinsinteraction networks 48,228 and
xi (b) Std,j ,= 0.39 cm xk are
x
and
- indicatorsinteraction networks with triangles
distributed
Yeast protein
257,978
Big tensor T has associated nonzeros
triangles
data methods too
The
~100,000,000,000
architectures
0
0
We work with it implicitly
1
the edges (i, i ), (j, j ), and
8
0

10. One canonical problem
PageRank
Personalized
PageRank
Semi-supervised"
learning on graphs
(
A
D
↵
f
T
↵A D
1
)x = f
adjacency matrix
degree matrix
regularization
“prior” or “givens”
Protein function
prediction
Gene-experiment
association
Network alignment
Food webs

11. One canonical problem
(
T
↵A D
1
)x = f
Vahab - clustering
Karl - clustering
Art – prediction
Jen
- prediction
Sebastiano – ranking/centrality

12. An example on a graph
PageRank by Google
(
↵A D
T
3
5
2
4
1
6
0
B
B
B
B
B
B
@
1
)x = f
2
31 2 3 2 3
1/6 1/2
0
0
0 0
x1
0
The Model
61/6
0
1/3 0 07C 6x2 7 607
6follow 0
1.61/6 1/2 0 uniformly with 6x 7 607
edges 1/3 0 07C 6 7 6 7
7C 3
6probability , and
7C 6 7 = 6 7
↵6
0
1/2
0
0 07C 6x4 7 617
61/6
7C 6 7 6 7
4randomly jump 1/3 0 15A 4x5 5 405
2. 1/6 0 1/2 with probability
1/6 , 0
0
1 0
x6
1
we’ll 0
assume everywhere is 0
equally likely
non-singular linear system ( < 1), non-negative inverse,
works with weights, directed & undirected graphs, weights
that don’t sum to less than 1 in each column, …

13. An example on a bigger graph
f has a single "
one here
Newman’s netscience graph
379 vertices
1828 non-zeros
“zero” on most of
the nodes

14. A special case
“one column” or “one node”
(
T
↵A D
x = column i of (
1
)x = ei
T
↵A D
localized solutions
1
)
1

15. An example on a bigger graph
Crawl of flickr from 2006 ~800k nodes, 6M edges, alpha=1/2
0
1.5
error
||xtrue – xnnz||1
10
1
0.5
0
−5
10
−10
10
−15
0
2
4
plot(x)
6
8
10
5
x 10
10
0
10
2
10
4
10
nonzeros
6
10

16. Complexity is complex
• Linear system – O(n3)
• Sparse linear sys. (undir.) – O(m log(m) )
where is a function of latest result on solving SDD
systems on graphs
• Neumann series – O(m log( )/log(tol))

17. Forsythe and Liebler, 1950

18. Monte Carlo methods for PageRank
K. Avrachenkov et al. 2005. Monte Carlo methods in PageRank
Fogaras et al. 2005. Fully scaling personalized PageRank.
Das Sarma et al. 2008. Estimating PageRank on graph streams.
Bahmani et al. 2010. Fast and Incremental Personalized PageRank
Bahmani et al. 2011. PageRank & MapReduce
Borgs et al. 2012. Sublinear PageRank
Complexity – “O(log |V|)”

19. Gauss-Seidel and Gauss-Southwell
Methods to solve A x = b
Update
x(k+1) = x(k) + ⇢j ej
such that
[Ax(k+1) ]j = [b]j
In words “Relax” or “free” the jth coordinate of your solution vector in
order to satisfy the jth equation of your linear system.
Gauss-Seidel repeatedly cycle through j = 1 to n
Gauss-Southwell use the value of j that has the highest magnitude residual
r(k) = b
Ax(k)

20. Matrix computations in a red-pill
Solve a problem better by
exploiting its structure!

21. Gauss-Seidel/Southwell for PageRank
w/ access to in-links & degs.
PageRankPull
(k +1)
j = blue node
Solve for
xj
xj(k+1)
(k)
↵xa /6
(k)
↵xb /2
(k)
↵xc /3
= fj
xj(k+1)
w/ access to out-links
PageRankPush
↵
X
i!j
xi(k ) /degi = fj
Let
b
a
c
j = blue node
r(k) = f + ↵AT D
1 (k )
x
(k+1)
= xj(k) + rj
(k +1)
=0
then
xj
Update
r(k +1) rj
(k
(k)
ra +1) = ra + ↵rj(k ) /3
(k
(k)
rb +1) = rb + ↵rj(k ) /3
r (k +1) = r (k) + ↵r (k ) /3
x(k)

22. Python code for PPR Push
# main loop!
while sumr > eps/(1-alpha):!
j = max(r.iteritems, !
key=(lambda x: r[x])!
rj = r[j]!
x[j] += rj!
r[j] = 0!
sumr -= rj!
deg = len(graph[j])!
for i in graph[j]:!
if i not in r: r[i] = 0.!
r[j] += alpha/deg*rj!
sumr += alpha/deg*rj!
# initialization !
# graph is a set of sets!
# eps is stopping tol!
# 0 < alpha < 1!
x = dict()!
r = dict()!
sumr = 0.!
for (node,fi) in f.items():!
r[node] = fi!
sumr += fi!
!
If f ≥ 0, this terminates when ||xtrue – xalg||1 <

23. Relaxation methods for PageRank
Arasu et al. 2002, PageRank computation and the structure of the web
Jeh and Widom 2003, Scaling personalized PageRank
McSherry 2005, A unified framework for PageRank acceleration
Andersen et al. 2006, Local PageRank
Berkhin 2007, Bookmark coloring algorithm for PageRank
Complexity – “O( |E| )”

24. 5
10
Monte Carlo
Relaxation
0
10
Sublinear"
“in theory”
||xtrue – xalg||1
gap
−5
10
Node degree=155
22k node, 2M edge 10−10
Facebook graph
gap
nnz(A)
10"
nnz(A)
Number of edges the
algorithm touches
4
10
How I’d solve it
6
10
8
10

25. Matrix computations in a red-pill
Solve a problem better by
exploiting its structure!

26. Some unity?
Theorem (Gleich and Kloster, 2013 arXiv:1310.3423)"
Consider solving personalized PageRank using the GaussSouthwell relaxation method in a graph with a Zipf-law in
the degrees with exponent p=1 and max-degree d, then
the work involved in getting a solution with 1-norm error is
⇤
⇣
work = O (1/") 1
1
↵
d(log d)2
⌘
Improve this?
* (the paper currently bounds exp(A D-1) ei but analysis yields this bound for PageRank)
** (this bound is not very useful, but it justifies that this method isn’t horrible in theory)

27. There is more structure
The one ring.
G1
G2
G3
(See C. Seshadhri’s talk for the reference)
G4

28. Further open directions
Nice to solve Unifying convergence results for Monte Carlo and
relaxation on large networks to have provably efficient, practical algs.
– Use triangles? Use preconditioning?
A curiosity Is there any reason to use a Krylov method?
– Staple of matrix computations, A ! AVk+1 = Vk Hk with Hk small
BIG gap Can we get algorithms with “top k” or “ordering” convergence?
– See Bahmani et al. 2010; Sarkar et al. 2008 (Proximity Search)
Important? Are the useful, tractable multi-linear problems on a network?
– e.g. triangles for network alignment; e.g. Kannan’s planted clique problem.
Supported by NSF CAREER 1149756-CCF
www.cs.purdue.edu/homes/dgleich