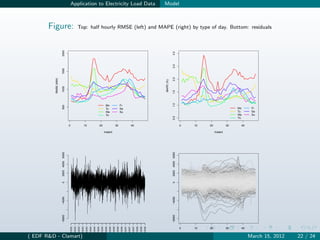
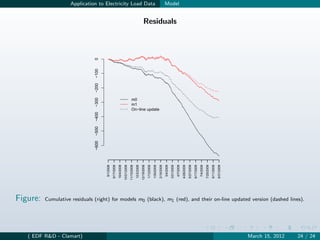
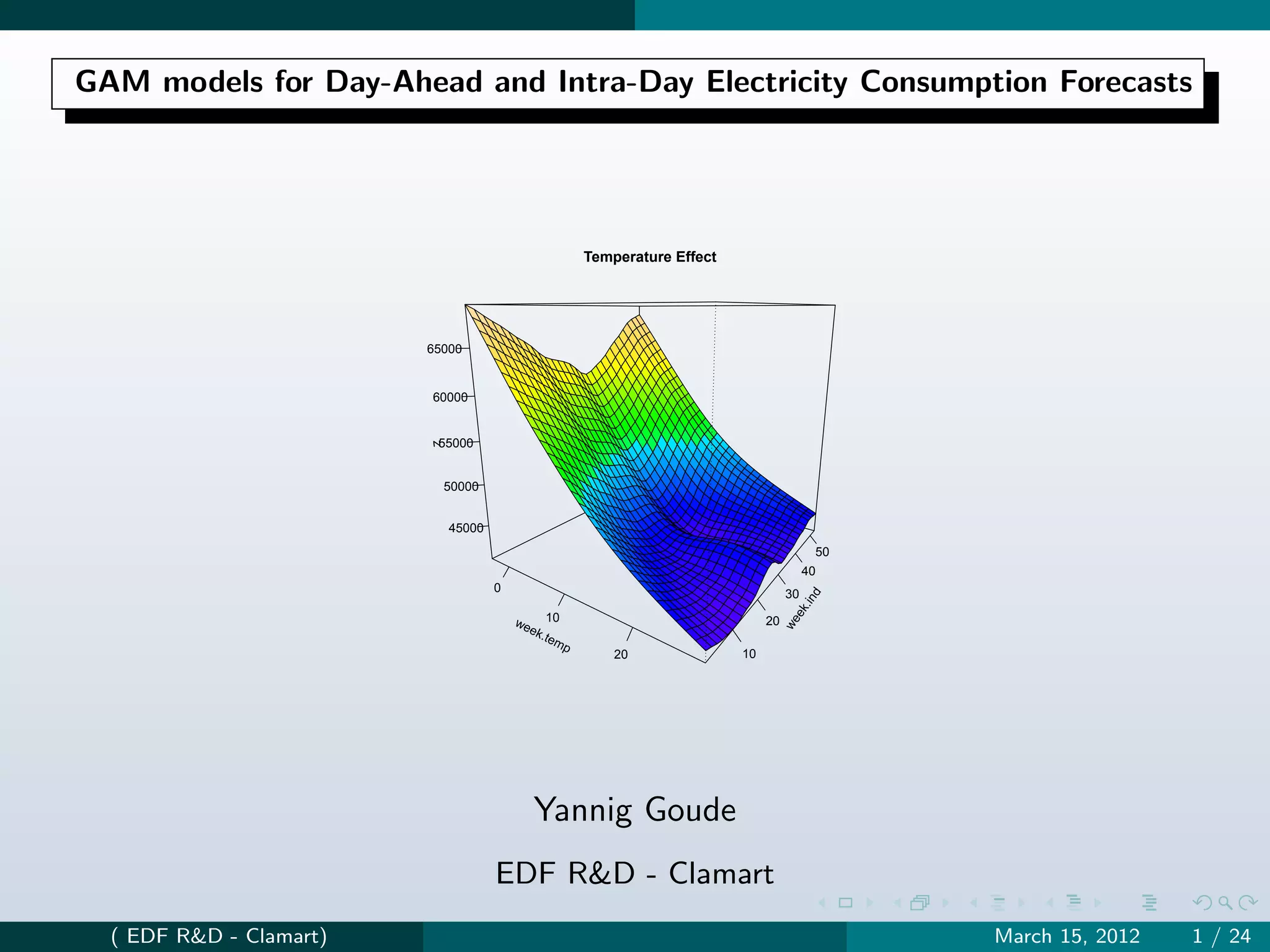
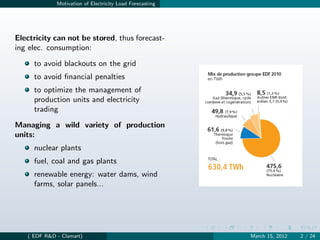
The document discusses generalized additive models (GAM) for short-term electricity load forecasting. GAMs are smooth additive models that decompose a response variable into additive components like trends, cyclic patterns, and nonlinear effects. They summarize how GAMs can model various drivers of electricity consumption, including temperature effects, day-of-week patterns, and lagged load values. Big additive models (BAM) allow applying GAMs to large electricity load datasets. BAMs use QR decomposition and online updating to efficiently estimate high-dimensional additive models.

1. GAM models for Day-Ahead and Intra-Day Electricity Consumption Forecasts
Temperature Effect
65000
60000
55000
z
50000
45000
50
40
0 30
d
.in
ek
we 10 20
we
ek.t
em
p
20 10
Yannig Goude
EDF R&D - Clamart
( EDF R&D - Clamart) March 15, 2012 1 / 24

2. Motivation of Electricity Load Forecasting
Electricity can not be stored, thus forecast-
ing elec. consumption:
to avoid blackouts on the grid
to avoid financial penalties
to optimize the management of
production units and electricity
trading
Managing a wild variety of production
units:
nuclear plants
fuel, coal and gas plants
renewable energy: water dams, wind
farms, solar panels...
( EDF R&D - Clamart) March 15, 2012 2 / 24

3. Motivation of Electricity Load Forecasting
Short-term load forecasting: from 1 day to a few hours horizon
( EDF R&D - Clamart) March 15, 2012 3 / 24

4. (Generalized) Additive smooth models
consider a univariate response y and corresponding predictors x1 , ..., xp
an additive smooth model has the following structure:
yi = Xi β + f1 (x1,i ) + f2 (x2,i ) + f3 (x3,i , x4,i ) + ... + εi
Xi β is the linear part of the model
functions fj are supposed to be smooth
εi :
iid
E (εi ) = 0,V (εi ) = σ 2
normality if needed (tests...)
More precisely, we want to solve the following pb:
minβ,fj ||y − X β − f1 (x1 ) − f2 (x2 ) + ...)2 + λ1 f1 (x)2 dx + λ2 f2 (x)2 dx + ...
( EDF R&D - Clamart) March 15, 2012 4 / 24

5. (Generalized) Additive smooth models
Estimation of the fj : basis expansion in a spline basis
kj
fj (x) = aj,q (x)βj,q
q=1
Then the additive model becomes
k1 k2
yi = Xi β + a1,q (x)β1,q + a2,q (x)β2,q + ... + εi
q=1 q=1
Unknowns:
choice of the spline basis, number-position of knots kj
β and aj,q
⇒ take large kj and proceed to penalized regression (ridge)
( EDF R&D - Clamart) March 15, 2012 5 / 24

6. (Generalized) Additive smooth models
Then the initial problem
minβ,fj ||y − X β − f1 (x1 ) − f2 (x2 ) + ...)2 + λ1 f1 (x)2 dx + λ2 f2 (x)2 dx + ...
becomes a linear regression problem:
minβ ||y − X β||2 + λ j β T Sj β
as fj (x)2 dx can be written as β T Sj β
absorbing aj,q (xi ) into Xi
Solution:
βλ = (X T X + λj Sj )−1 X T y
( EDF R&D - Clamart) March 15, 2012 6 / 24

7. (Generalized) Additive smooth models
How to choose the penalization parameter λ?
without any penalisation: β0 = (X T X )−1 X T y
regularised: βλ = (X T X + λj Sj )−1 X T y
β λ = Fλ β 0
Where
Fλ = (X T X + λj Sj )−1 X T X
tr (Fλ ): estimated degrees of freedom
( EDF R&D - Clamart) March 15, 2012 7 / 24

8. (Generalized) Additive smooth models
How to choose the penalization parameter λ?
( EDF R&D - Clamart) March 15, 2012 8 / 24

9. (Generalized) Additive smooth models
Ordinary Cross Validation
leave one observation yi
estimate a model µ−i on the new data set
forecast yi with µ−i
i
do that for all i
choose the λ that minimizes the OCV score:
n
V0 (λ) = (yi − µ−i )2 /n
i
i=1
Pb: calculation time
Generalized Cross Validation [Craven and Wahba (1979)]
Vg (λ) = n y − X βλ |2 /(n − tr (Fλ ))2
Advantages of GCV:
λ is obtained by numerical minimization of Vg (few comp. cost)
Vg (λ) is invariant when doing useful transf. of the data (on-line update, big data)
⇒ Software: R, package mgcv (see[Wood (2001)] and [Wood (2006)])
( EDF R&D - Clamart) March 15, 2012 9 / 24

10. From GAM to BAM
BAM: Big Additive Models
⇒ for huge data sets (more than 10 000 observations) we use the QR decomposition:
X = QR, f = Q T y and denote ||r ||2 = ||y ||2 − ||f ||2
Q orth. matrix, R upper triang.
then we have:
n||f − R βλ ||2 + ||r ||2
Vg (λ) =
(n − tr (Fλ ))2
where Fλ is now (R T R + λj Sj )−1 R T R
⇒ Once we have R, f and ||r ||2 , X plays no further part
( EDF R&D - Clamart) March 15, 2012 10 / 24

11. From GAM to BAM
⇒ Application for large data sets:
X0 y0
X is too big and has to be split: , similarly y =
X1 y1
R0
form QR dec. X 0 = Q0 X0 and = Q1 R see section 12.5 of
X1
[Golub and Van Loan (1996)]
T
Q0 0 Q0 y0
then X = QR with Q = Q1 and Q T y = Q1
T
0 I y1
⇒ On-line update
X0 , y0 past data, X1 , y1 last observations
Use the new data X1 , y1 to update R, f and ||r ||2
Re-estimate λ and βλ (previous values can be used as starting values for the
numerical optimization)
( EDF R&D - Clamart) March 15, 2012 11 / 24

12. ( EDF R&D - Clamart)
40000 50000 60000 70000 80000 90000
1/9/2002
13/1/2003
28/5/2003
9/10/2003
21/2/2004
4/7/2004
16/11/2004
31/3/2005
Application to Electricity Load Data
12/8/2005
25/12/2005
Trend
8/5/2006
20/9/2006
1/2/2007
16/6/2007
28/10/2007
Electricity Data
10/3/2008
23/7/2008
4/12/2008
18/4/2009
31/8/2009
March 15, 2012
12 / 24

13. ( EDF R&D - Clamart)
30000 40000 50000 60000 70000 80000
1/1/2006
20/1/2006
8/2/2006
27/2/2006
18/3/2006
7/4/2006
26/4/2006
15/5/2006
Application to Electricity Load Data
3/6/2006
22/6/2006
12/7/2006
31/7/2006
19/8/2006
Yearly Pattern
7/9/2006
26/9/2006
Electricity Data
16/10/2006
4/11/2006
23/11/2006
12/12/2006
31/12/2006
March 15, 2012
13 / 24

14. ( EDF R&D - Clamart)
35000 40000 45000 50000 55000
1/6/2006
2/6/2006
4/6/2006
5/6/2006
7/6/2006
8/6/2006
10/6/2006
12/6/2006
Application to Electricity Load Data
13/6/2006
15/6/2006
16/6/2006
18/6/2006
19/6/2006
Weekly Pattern
21/6/2006
23/6/2006
Electricity Data
24/6/2006
26/6/2006
27/6/2006
29/6/2006
30/6/2006
March 15, 2012
14 / 24

15. Application to Electricity Load Data Electricity Data
Daily Pattern
70000
Mo Fr
Tu Sa
65000
We Su
60000
55000 Th
Load
50000
45000
40000
0 10 20 30 40
Instant
( EDF R&D - Clamart) March 15, 2012 15 / 24

16. Load (MW)
60000 65000 70000 75000 80000
0
10
Normal
( EDF R&D - Clamart)
20
Instant
30
Special Tariff
40
Application to Electricity Load Data
55000 60000 65000 70000 75000 80000 85000
Special Days
20/12/2007
20/12/2007
21/12/2007
Electricity Data
22/12/2007
23/12/2007
24/12/2007
25/12/2007
25/12/2007
26/12/2007
27/12/2007
28/12/2007
29/12/2007
30/12/2007
30/12/2007
31/12/2007
1/1/2008
2/1/2008
3/1/2008
4/1/2008
4/1/2008
March 15, 2012
16 / 24

17. Application to Electricity Load Data Electricity Data
Load-Temperature
( EDF R&D - Clamart) March 15, 2012 17 / 24

18. Application to Electricity Load Data Electricity Data
75000
Load-Cloud Cover
8
70000
6
Cloud cover (Octets)
Load (MW)
65000
4
2
60000
0
0 10 20 30 40 0 10 20 30 40
Instant Instant
( EDF R&D - Clamart) March 15, 2012 18 / 24

19. Application to Electricity Load Data Model
Lt = f1 (Lt−48 , It ) IHH +f2 (Lt−48 , It ) IHW +f3 (Lt−48 , It ) IWH +f4 (Lt−48 , It ) IWW
+ g1 (Tt , It ) + g2 (Tt−48 , Tt−96 ) + g3 (Cloudt )
+ h(Toyt , It )
48
+ i=1 γi Spec.Tarift
11
+ j=1 αj
+ s(t)
+ εt
fj s: lagged load effects
gj s: meteo. effects
hs: yearly pattern, Toy is time of year
γi : special tariff effect by half-hour of the day
αj mean load for: sunday, monday, tuesday,...,saturday, HH,HW,WH and WW days
s(t) is the trend
Estimation period: september 2002 - august 2008
Forecasting period: september 2008 - august 2009
( EDF R&D - Clamart) March 15, 2012 19 / 24

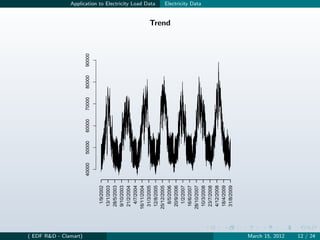
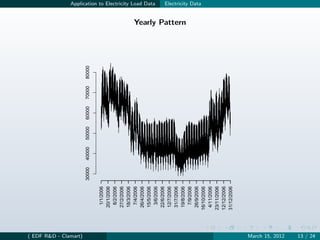
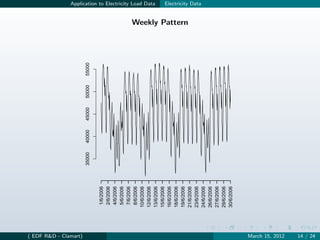
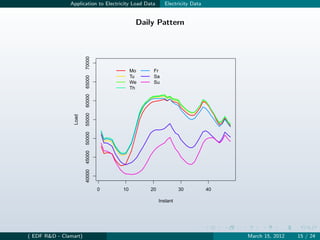
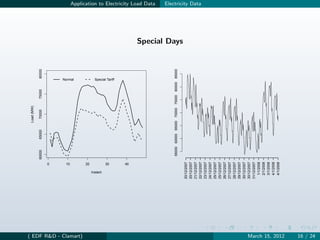
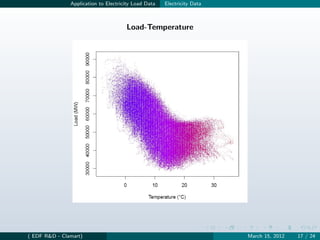
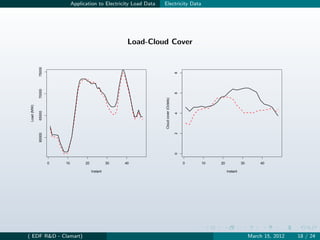
20. Application to Electricity Load Data Model
GAM Model
10000
Temperature Effect
5000
70000
65000
Load (MW)
0
L[t]
60000
−5000
55000
50000 40
30 30
−10000
20 20
I[t]
T[t 10 Mo Fr Su
] 10
0 we Sa
0
0 10 20 30 40
Hour
Yearly Cycle Trend
10000
80000
70000
5000
60000
z
0
50000
40000
−5000
40
0.0 30
0.2
0.4 20
nt
Po
sta
san 0.6
In
10
−10000
0.8
0
120000 140000 160000 180000 200000 220000 240000
t
( EDF R&D - Clamart) March 15, 2012 20 / 24

21. Application to Electricity Load Data Model
Lagged Load Effect, WW Lagged Load Effect, WH
80000
70000
70000
60000
L[t]
60000
L[t]
50000
50000
40000
40000
40 30000 40
80000 30 80000 30
70000 20 70000 20
60000 60000
]
]
I[t
I[t
L[t 50000 10 L[t 50000 10
−1 −1
] 40000 ] 40000
30000 0 30000 0
Lagged Load Effect, HW Lagged Load Effect, HH
30000
20000
80000
L[t]
10000
L[t]
60000 0
−10000
40000
40 40
80000 30 80000 30
70000 20 70000 20
60000 60000
]
]
I[t
I[t
L[t 50000 10 L[t 50000 10
−1 −1
] 40000 ] 40000
30000 0 30000 0
( EDF R&D - Clamart) March 15, 2012 21 / 24

22. RMSE (MW)
−8000 −4000 0 2000 4000 6000 500 1000 1500 2000
0
9/1/2002
Figure:
12/19/2002
4/8/2003
( EDF R&D - Clamart)
8/12/2003
10
12/4/2003
3/22/2004
7/26/2004
11/17/2004
20
3/7/2005
7/6/2005
Tu
Th
Mo
We
10/23/2005
Instant
2/18/2006
30
6/20/2006
Fr
10/8/2006
Su
Sa
2/3/2007
6/4/2007
40
9/21/2007
1/17/2008
5/6/2008
8/31/2008
Application to Electricity Load Data
MAPE (%)
−8000 −4000 0 2000 4000 6000 0.5 1.0 1.5 2.0 2.5 3.0
Model
0
0
10
10
20
20
Instant
30
30
Tu
Th
Mo
We
40
40
Fr
Su
Sa
Top: half hourly RMSE (left) and MAPE (right) by type of day. Bottom: residuals
March 15, 2012
22 / 24

23. Application to Electricity Load Data Model
Performances
Model RMSE (MW) MAPE (%) RGCV score
Estimation set
m0 831 1.17 882
m1 1024 1.46 806
Forecasting set
m0 1220 1.87
On-line m0 1048 1.49
m1 1156 1.62
On-line m1 1109 1.53
( EDF R&D - Clamart) March 15, 2012 23 / 24

24. Application to Electricity Load Data Model
Residuals
0
−100
−200
−300
m0
m1
On−line update
−400
−500
−600
9/1/2008
9/17/2008
10/4/2008
10/21/2008
11/15/2008
12/2/2008
12/19/2008
1/13/2009
1/30/2009
2/16/2009
3/4/2009
3/21/2009
4/7/2009
4/28/2009
5/27/2009
6/17/2009
7/4/2009
7/25/2009
8/11/2009
8/31/2009
Figure: Cumulative residuals (right) for models m0 (black), m1 (red), and their on-line updated version (dashed lines).
( EDF R&D - Clamart) March 15, 2012 24 / 24

25. Application to Electricity Load Data Model
Craven and Wahba (1979) ”Smoothing noisy data with spline functions: estimated the correct degree of smoothing by
the method of general cross validation”. Numerische Mathematik 31, 377-403.
Golub and Van Loan (1996) ”Matrix Computations, 3rd edition”. John Hopkins Studies in the Mathematical Sciences.
Green and Silverman (1994) ”Nonparametric Regression and Generalized Linear Models”. Chapman and Hall.
Hastie and Tibshirani (1990) ” Generalized Additive Models”. Chapman and Hall.
Pierrot and Goude (2011) ”Short-Term Electricity Load Forecasting With Generalized Additive Models”, Proceedings of
ISAP power 2011.
Wahba (1990) ”Spline Models of Observational Data”. SIAM
Wood (2001) mgcv:GAMs and Generalized Ridge Regression for R. R News 1(2):20-25
Wood and Augustin (2002) ”GAMs with integrated model selection using penalized regression splines and applications to
environmental modelling”. Ecological Modelling 157:157-177
Wood (2006)Generalized Additive Models, An Introduction with R (Chapman and Hall, 2006)
( EDF R&D - Clamart) March 15, 2012 24 / 24