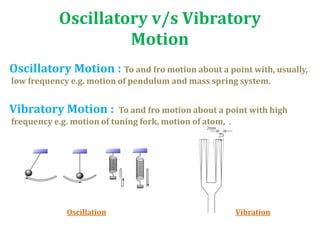
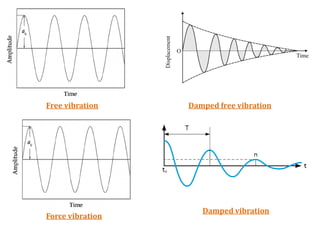
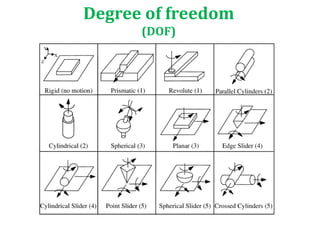
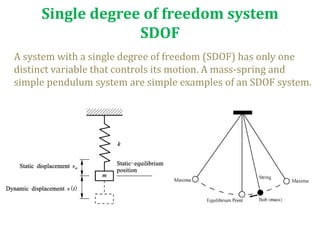
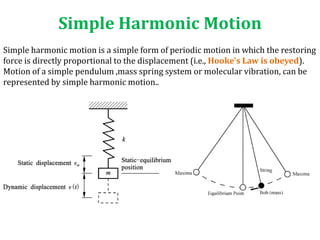
The document discusses types of motion, focusing on periodic and non-periodic motions, and outlines characteristics of periodic motion including time period, frequency, amplitude, and degrees of freedom. It explains simple harmonic motion (SHM), its relationship to Hooke's law, and the concepts of potential and kinetic energy in vibratory systems. Additionally, it covers forced vibrations and resonance, detailing the impact of external forces on system behavior.

1. Assigned by Dr. Khubab Shaker
Prepared by Engr. Habibullah
Vibrations

2. Motion
Change in position w.r.t Time

3. We have two types of periodic
Motions in all time

4. Types of Motion
Periodic Motion: Repetition of motion itself after particular interval
of time.
Motion of pendulum Motion of spring
Circular motion Motion of Satellite
around earth

5. Types of Motion
Non Periodic Motion: Does not repeat motion itself or does
repeat irregular manner.
Projectile Motion Linear Motion
Irregular motion

6. Types of Periodic Motion
Circular Motion : Motion along a circular path around a point.
All circular motions are periodic but all Periodic motion are
not circular.

7. Types of Periodic Motion
Oscillatory/ Vibratory: To and fro motion about a point
Motion
Pendulum Spring mass system

8. Oscillatory v/s Vibratory
Motion
Oscillatory Motion : To and fro motion about a point with, usually,
low frequency e.g. motion of pendulum and mass spring system.
Vibratory Motion : To and fro motion about a point with high
frequency e.g. motion of tuning fork, motion of atom, .
Oscillation Vibration

9. Types of vibration
 Free or natural vibration:
Object vibrate freely without Influence of external disturbance
after initial excitation e.g. motion of mass spring system.
 Force vibration :
Object vibrate under the Influence of external disturbance
e.g. vibration of engine.
 Damp vibration:
Object dissipate energy gradually during vibration.

10. Force vibration
Damped free vibration
Damped vibration
Free vibration

11. Degree of freedom
(DOF)
1. The minimum number of quadrants required to describe the position of
a particle in space.
2. The minimum number of inputs required to actuate a mechanism.
3. The number of degrees of freedom for a system is the number of
kinematic ally independent variables necessary to completely describe
the motion of every particle in the system.

12. Degree of freedom
(DOF)

13. Characteristics of periodic motion
1. Time Period:
Time required to complete one cycle is called a Time period and it is normally
expressed in seconds (s). T=2𝝅/𝝎
2. Cycle:
It is motion completed during one time period.
3. Frequency:
It is the number of cycles describes in one second. This SI unit is Hertz.
𝒇 = 𝝎/𝟐𝝅
4. Amplitude:
The maximum displacement of the vibrating body from its equilibrium/mean position.
5. Natural Frequency:
When no external force acts on the system after giving its an initial displacement,
the body vibrates. The vibration is called as free vibration and the frequency is called
Natural frequency. This is expressed in rad/sec or Hertz.

14. Single degree of freedom system
SDOF
A system with a single degree of freedom (SDOF) has only one
distinct variable that controls its motion. A mass-spring and
simple pendulum system are simple examples of an SDOF system.

15. Simple Harmonic Motion
Simple harmonic motion is a simple form of periodic motion in which the restoring
force is directly proportional to the displacement (i.e., Hooke's Law is obeyed).
Motion of a simple pendulum ,mass spring system or molecular vibration, can be
represented by simple harmonic motion..

16. Hook’s Law
Whenever the restoring force is directly proportional to displacement, the
simplest oscillations happen. Hooke's law gives relation between force and
displacement:
F=-k x
F is the restoring force.
x is the displacement from equilibrium.
k is a spring constant related to the difficulty in deforming the system.
(Negative signe shows direction of displacement relative to force).

17. Hook’s Law
The extension of the spring is linearly proportional to the force.

18. Conditions for SHM
1. Restoring force directly proportional to displacement
2. Acceleration directly proportional to displacement

19. Differential equation of Linear SHM

20. Uniform circular motion as a SHM
Here,

22. The velocity and acceleration can be
calculated as functions of time.
+A
o
-A

23. Energy in SHM
potential energy of a mass-spring system is given by:
PE = ½ kx2
The total mechanical energy of system:
E = Kinetic Energy + Potential Energy = Constt.
= Constt.
The total mechanical energy will be conserved, as we are
assuming the system is frictionless.

24. Energy in Simple Harmonic Motion
If the mass is at the extreme position,
the energy is totally potential Energy.
If the mass is at the mean /equilibrium
point, the energy is totally kinetic.
Total energy is at the turning points:

25. The total energy of system is, therefore ½ kA2
And energy at any instant of time:
Here ,
A is max. displacement from mean position.
x is displacement from mean position at any
interval of time.

26. Potential
Energy
Kinetic
Energy
Total Energy
Energy in SHM
-A A
Mean Position
Energy

27. Force vibration
Forced vibrations occur when there is a periodic
external force. This force may or may not have the
same period as the natural frequency of the system.
If the frequency is the same as the natural frequency,
the amplitude becomes quite large. This is called
resonance.

28. 𝒎𝒙 + 𝒄𝒙 + 𝒌𝒙 = 𝑭𝟎 𝐬𝐢𝐧 𝝎𝒇𝒕
𝑭𝟎 is the external force
ω is the driving frequency
𝒎𝒙 is inertial Force
𝒄𝒙 is damping force
𝒌𝒙 is spring force
Where,
This equation can be solved exactly for any driving
force using complimentary function and particular
integrals.

30. The sharpness of the resonant peak depends on the damping. If
the damping force is small (A), it can be quite sharp, if the
damping force is larger (B), it is less sharp.

32. Thanks