The document discusses mathematical relations and functions. It defines Cartesian products and relations. Cartesian products combine elements from two sets into ordered pairs. Relations are subsets of Cartesian products that satisfy a given condition. The document provides examples of calculating Cartesian products and defining relations for given sets. It also establishes properties of Cartesian products, such as A × (B ∪ C) = (A × B) ∪ (A × C) and discusses domains and ranges of relations.












![F F 7
F x = y
y - 1
F F x y - 1 = y
กก F F x2
(y 1) = y2
=> y2
x2
y + x2
= 0
กF ก y F y =
2 2 2
x x (x - 4)
2
±
F 2 2
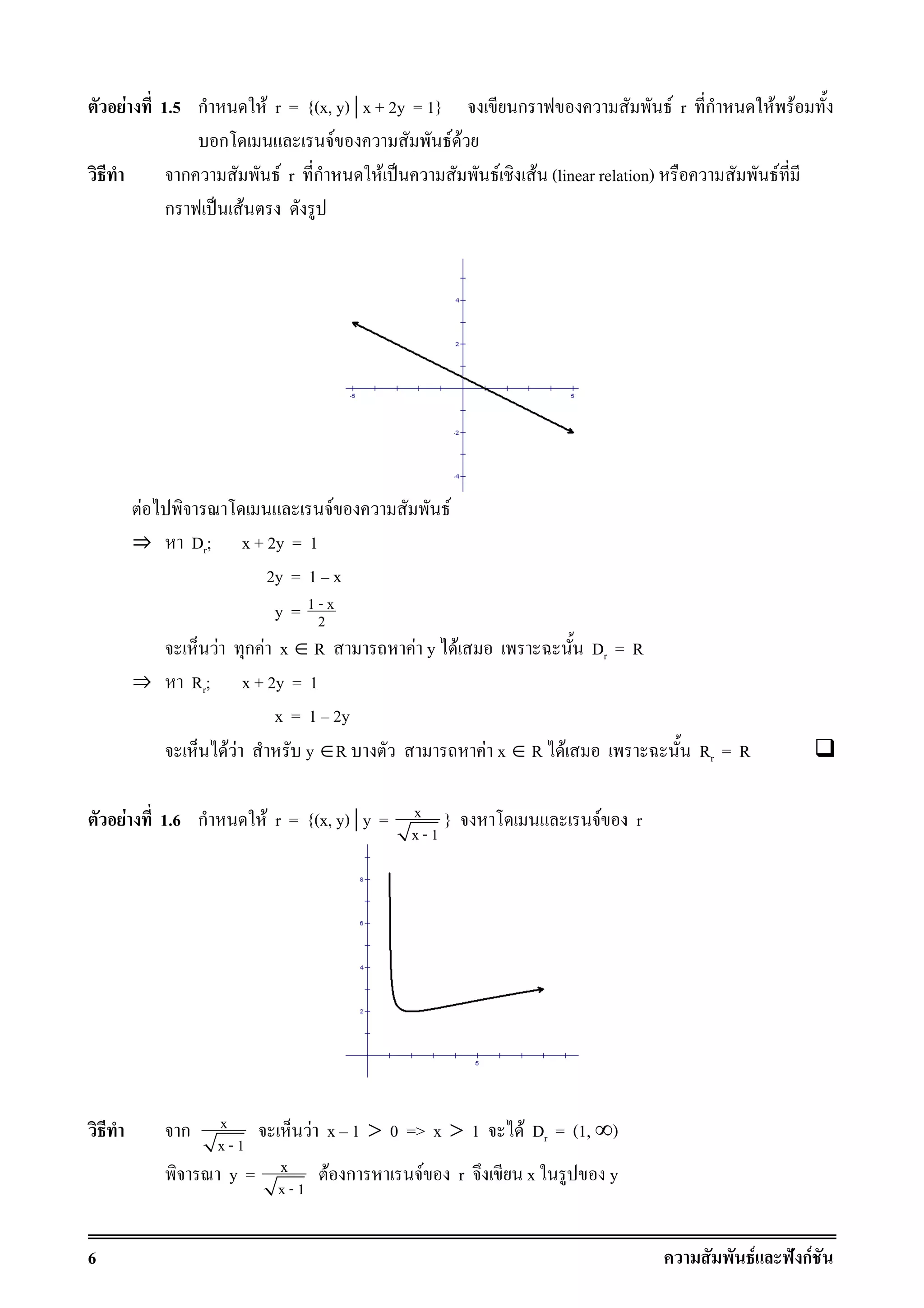
x (x - 4) ≥ 0 กF ก F ( ∞, 2] ∪ [2, ∞)
F x
x - 1
> 0 ก F x {( ∞, 2] ∪ [2, ∞)} ∩ [0, ∞) = [2, ∞)
F F Rr = [2, ∞)
1.3 ก F
F 1.7 ก F r = {(x, y) | y = 5 - 2x
3 } r 1
ก 1.4 F F x ˈ y y ˈ x ก F ก
F F ก r 1
= {(x, y) | x = 5 - 2y
3 }
F F x ก F
=> ก x = 5 - 2y
3 F F 3x = 5 2y
2y = 5 3x y = 5 - 3x
2
r 1
= {(x, y) | y = 5 - 3x
2 }
1.4
ก F r ˈ F ก A B F r 1
ˈ F ก B A
r 1
= {(y, x) | (x, y) ∈ r}](https://image.slidesharecdn.com/lecture005-relationsfunction-140713074949-phpapp02/75/relations-function-15-2048.jpg)



![F F 11
ก F ˆ กF ก ก F
F ˆ กF F 2 ˆ กF f : A → B ก g : A → B F F F F
f = g F F F
F ก F f : A → B g : A → B
(fl) F f = g F f(x) = g(x) ก x ∈ A
F F y ∈ B (x, y) ∈ f
F f = g F F (x, y) ∈ g
y = f(x) y = g(x) f(x) = g(x)
(›) F f(x) = g(x)
(⊆) F (x, y) ∈ f F x ∈ A y ∈ B y = f(x)
F ก F F F y = g(x) F
(x, y) ∈ g f ⊆ g
(⊇) F ก ⊆
ก F F f = g
ก F F ˈ
2.2
F f ˈ F ก A B ก F F f ˈ ˆ กF ก A B (function from A to B)
F ก F f : A → B ก F
1) Df = A
2) ∀x ∈ A, ∀y, z ∈ B, [(x, y) ∈ f - (x, z) ∈ f fl y = z]
2.1
ก F f : A → B g : A → B F f = g ก F f(x) = g(x) ก x ∈ A](https://image.slidesharecdn.com/lecture005-relationsfunction-140713074949-phpapp02/75/relations-function-19-2048.jpg)


![14 F ˆ กF
2.2 ˆ กF ˆ กF
F 2.3 ก F f(x) = x2
2 x ∈ [0, 3] F f(x) ก F ˈ ˆ กF
ˆ กF
ก F x1, x2 ∈ [0, 3] x1 < x2 F F
x1
2
< x2
2
3x1
2
< 3x2
2
3x1
2
2 < 3x2
2
2
f(x1) < f(x2)
F f ˈ ˆ กF F [0, 3]
ก F ˆ กF ก F ˈ ˆ กF ˆ กF ก ก
2.4 F F กก ก ˆ กF ( F ก F F ) F
F
F 2.4 ก ˆ กF f ก F F 2.3 ก y = f(x) F F
F [ 3, 3] ˈ ˆ กF ˆ กF
ก y = f(x) = x2
2 ก F
2.4
ก F f ˈ ˆ กF ก R R F A ⊆ Df
1) f ˈ ˆ กF (increasing function) A ก F x1, x2 ∈ A F x1 < x2 F
f(x1) < f(x2)
2) f ˈ ˆ กF (decreasing function) A ก F x1, x2 ∈ A F x1 < x2 F
f(x1) > f(x2)](https://image.slidesharecdn.com/lecture005-relationsfunction-140713074949-phpapp02/75/relations-function-22-2048.jpg)
![F F 15
ก F ˈ ก y = x2
2 ก x ∈ [ 3, 3] F F ก ˈ 2 F
[ 3, 0] F ก F ก F [0, 3] F ก F ก F [0, 3]
x F f(x) F F F ˆ กF f F [0, 3] ˈ ˆ กF
ก F [ 3, 0] F x F f(x)
ก ก ก F x F f(x) F F ก
F F f(x) = x2
2 ˈ ˆ กF F [ 3, 0]
ʿก 2.2
1. ก F f(x) = 2
1
x + 1
F f(x) ˈ ˆ กF ก x ∈ [0, 2]
2. ก F f(x) = 4x2
3 F F ก x ∈ [0, 1] F f ˈ ˆ กF
3. F F F 1 F 2 ˈ Fก
2.3 ˆ กF ก (Composite function)
F ก
1. ก 2.5 F F Dgof = A
2. ˆ กF ก f g F F F F F
F Rf ∩ Dg ≠ φ F ˆ กF ก f g F F ก ก ˆ กF ก
g f F F F F Rf ∩ Dg ≠ φ F ˆ กF ก
g f F F F F F F F
F 2.5 ก F f(x) = 2x + 1 g(x) = x2
+ 3 F gof F F F Fก
gof ก F
ก Rf = R Dg = R Rf ∩ Dg ≠ φ F gof
2.5 F F gof(x) = g(f(x))
= g(2x + 1)
= (2x + 1)2
+ 3
2.5
ก F f : A → B g : B → C F gof : A → C](https://image.slidesharecdn.com/lecture005-relationsfunction-140713074949-phpapp02/75/relations-function-23-2048.jpg)
![16 F ˆ กF
= 4x2
+ 4x + 1 + 3
= 4x2
+ 4x + 4
F 2.6 ก ˆ กF f g F 2.5 F fog F F F Fก F fog
ก F
ก Rg = [3, ∞) Df = R Rg ∩ Df ≠ φ F fog
2.5 F F fog(x) = f(g(x))
= f(x2
+ 3)
= 2(x2
+ 3) + 1
= 2x2
+ 6 + 1
= 2x2
+ 7
F 2.7 ก F f(x) = 2
1
x - 2x - 3
g(x) = x 2 F ˆ กF ก g f
F
ก Rg ∩ Df = R ∩ [R { 1, 3}] = R { 1, 3} ≠ φ F fog
ก fog(x) = f(g(x)) = f(x 2)
= 2
1
(x - 2) - 2(x - 2) - 3
= 2
1
x - 6x + 5
F 2.8 ก F 2.7 F fog(0)
ก fog(x) = 2
1
x - 6x + 5
F F fog(0) = 2
1
0 - 6(0) + 5
= 1
5](https://image.slidesharecdn.com/lecture005-relationsfunction-140713074949-phpapp02/75/relations-function-24-2048.jpg)
![F F 17
F ˈ ก F F ก F F ˆ กF ก ˈ
ˆ กF F
F 1) F ∀x1, x2 ∈ A, [gof(x1) = gof(x2) fl x1 = x2]
F x1, x2 ∈ A F F y ∈ C (x1, y) ∈ gof (x2, y) ∈ gof
y = gof(x1) y = gof(x2)
F gof(x1) = gof(x2)
ก g ˈ ˆ กF F f(x1) = f(x2)
ก f ˈ ˆ กF F F F x1 = x2 F ก
2) F Rgof = C
(⊆) F y ∈ Rgof F F x ∈ A z ∈ B (x, z) ∈ f (z, y) ∈ g
y = g(z)
y ∈ C
(⊇) F y ∈ C F F x ∈ A (x, y) ∈ gof
y = gof(x)
y ∈ Rgof
F F Rgof = C F ก
ʿก 2.3
1. ก F A, B, C ˈ F ˈ F f : A → B g : B → C F
gof : A → C Dgof = A
2. F f : A → B B F g : B → C, h : B → C F F gof = hof
F g = h
2.2
F f : A → B g : B → C F F F F gof : A → C ˈ
ˆ กF F C](https://image.slidesharecdn.com/lecture005-relationsfunction-140713074949-phpapp02/75/relations-function-25-2048.jpg)











![F F 29
3.2.2 F ˆ กF ก
2 F ก ก F ˆ กF F F
F ˆ กF ก F F
ˆ กF F
y = sin x R [ 1, 1]
y = cos x R [ 1, 1]
y = tan x R { n
2
π | n ˈ } R
y = cosec x R {nπ | n ˈ } R ( 1, 1)
y = sec x R { n
2
π | n ˈ } R ( 1, 1)
y = cot x R {nπ | n ˈ } R
3.2.3 ก ˆ กF ก
ก ก ก ˆ กF ก F F F F ก ก F
ก F ˆ กF ก F ก F F
3.2 ก y = sin x F [ 2ππππ, 2ππππ]
3.3 ก y = cos x F [ 2ππππ, 2ππππ]](https://image.slidesharecdn.com/lecture005-relationsfunction-140713074949-phpapp02/75/relations-function-37-2048.jpg)
![30 F ˆ กF
3.4 ก y = tan x F ( ∞∞∞∞, ∞∞∞∞)
ʿก 3.2
1. ก F y = cos x + sin x ก x ∈ [0, π] F F F
ก ˆ กF ก F F
2. ก F f(x) = sin x F ˆ กF f ก F ˈ ˆ กF F ก x ∈ [0, 2
π ]](https://image.slidesharecdn.com/lecture005-relationsfunction-140713074949-phpapp02/75/relations-function-38-2048.jpg)

![32 F ˆ กF
F 3.7 F cos2 5
12
π + sin2 5
6
π + sin2 5
12
π + cos2 7
6
π
ก. 2 . 3
. 11
4 . 3
2
. F F ก F
ก F cos2 5
12
π + sin2 5
6
π + sin2 5
12
π + cos2 7
6
π ก F F F
(cos2 5
12
π + sin2 5
12
π ) + (sin2 5
6
π + cos2 7
6
π )
= 1 + (sin2 5
6
π + cos2 7
6
π )
= 1 + [sin2
(π 6
π ) + cos2
(π + 6
π )]
= 1 + (sin2
6
π + cos2
6
π )
= 1 + 1
= 2
ʿก 3.3
1. F ก ก F ก ก F F ˈ
1) cos2
θ cot θ + sin2
θ tan θ + 2 sin θ cos θ = tan θ + cot θ
2) tan2
θ sin2
θ = tan2
θ sin2
θ
3)
2
2
cosec
1 + tan
θ
θ
= cot2
θ
2. F 3.1 F 4) F 5) ˈ](https://image.slidesharecdn.com/lecture005-relationsfunction-140713074949-phpapp02/75/relations-function-40-2048.jpg)


![F F 35
( )sin (3A - A)
sin A cos A ⋅( )sin (3A + A)
sin A cos A = 2
( )sin2A
sinAcosA ⋅( )sin4A
sinAcosA = 2
( )sin2A
sinAcosA ⋅( )sin2(2A)
sinAcosA = 2
( )2sinAcosA
sinAcosA ⋅( )2sin2Acos2A
sinAcosA = 2
( )2sinAcosA
sinAcosA ⋅( )4sinAcosAcos2A
sinAcosA = 2
2 ⋅ 4 cos 2A = 2
cos 2A = 1
4
ก F F ˈ ก ก F ก ˈ
ก
F F ก F F 2) F 3) F F ก F ก F F ก
F F F F F ˈ ʿก
2) ก 2 sin( )x + y
2 cos( )x - y
2 = 2 sin( )yx
2 2+ cos( )yx
2 2-
ก F A = x
2 B = y
2 F F F F F F
= 2 sin (A + B) cos (A B)
= 2 (sin A cos B + cos A sin B)(cos A cos B + sin A sin B)
= 2 (sin A cos B ⋅ cos A cos B + cos A sin B ⋅ cos A cos B
+ sin A cos B ⋅ sin A sin B + cos A sin B ⋅ sin A sin B)
= 2 (sin A cos A cos2
B + cos2
A sin B cos B + sin2
A cos B sin B + cos A sin A sin2
B)
= 2 [sin A cos A (cos2
B + sin2
B) + sin B cos B (cos2
A + sin2
A)]
= 2 (sin A cos A + sin B cos B) ( ก cos2
B + sin2
B = 1 cos2
A + sin2
A = 1)
= 2 sin A cos A + 2 sin B cos B
= sin 2A + sin 2B
3.4 ก ก F ˈ
1) cos x + cos y = 2 cos( )x + y
2 cos( )x - y
2
2) sin x + sin y = 2 sin( )x + y
2 cos( )x - y
2
3) cos x cos y = 2 sin( )x + y
2 sin( )x - y
2
4) sin x sin y = 2 cos( )x + y
2 sin( )x - y
2](https://image.slidesharecdn.com/lecture005-relationsfunction-140713074949-phpapp02/75/relations-function-43-2048.jpg)
![36 F ˆ กF
F A = x
2 B = y
2
F F 2 sin( )x + y
2 cos( )x - y
2 = sin x + sin y
3) ก 2 sin( )x + y
2 sin( )x - y
2 = 2 sin( )yx
2 2+ sin( )yx
2 2-
ก F A = x
2 B = y
2 F F F F F F
= 2 sin (A + B) sin (A B)
= 2 (sin A cos B + cos A sin B)(sin A cos B cos A sin B)
= 2 [(sin A cos B)2
(cos A sin B)2
]
= 2 sin2
A cos2
B + 2 cos2
A sin2
B
= 2 sin2
A cos2
B + 2 (1 sin2
A)(1 cos2
B)
= 2 sin2
A cos2
B + 2 (1 sin2
A cos2
B + sin2
A cos2
B)
= 2 sin2
A cos2
B + 2 (1 sin2
A) 2 cos2
B + 2 sin2
A cos2
B
= 2 (1 sin2
A) 2 cos2
B
= 2 cos2
A 2 cos2
B
= (2 cos2
A 1) (2 cos2
B 1)
= cos 2A cos 2B
F A = x
2 B = y
2
F F 2 sin( )x + y
2 sin( )x - y
2 = cos x cos y F ก
ʽ F F F ก ก ก ก ˈ ก F
ก
F 1) ก cos(x + y) + cos(x - y)
2
= (cos x cos y - sin x sin y) + (cos x cos y + sin x sin y)
2
= 2 cos x cos y
2 = cos x cos y
2) ก cos (x - y) - cos (x + y)
2
= (cos x cos y + sin x sin y) - (cos x cos y - sin x sin y)
2
= 2 sin x sin y
2 = sin x sin y
3.5 ก ˈ ก F
1) cos x cos y = cos (x + y) + cos (x - y)
2
2) sin x sin y = cos (x - y) - cos (x + y)
2
3) sin x cos y = sin (x - y) + sin (x + y)
2](https://image.slidesharecdn.com/lecture005-relationsfunction-140713074949-phpapp02/75/relations-function-44-2048.jpg)




















![58 F ˆ กF
F F
F 4.8 F log93, log9(3x
2), log9(3x
+ 16) ˈ F ก ก ก S ˈ
ก F ก ก F 3S
F F ก F
ก log93, log9(3x
2), log9(3x
+ 16) ˈ F ก ก ก
F F d1 = log9(3x
2) log93
= log9( )x
3 - 2
3
d2 = log9(3x
+ 16) log9(3x
2)
= log9( )x
x
3 + 16
3 - 2
F d1 = d2 ( ก ˈ )
log9( )x
3 - 2
3 = log9( )x
x
3 + 16
3 - 2
x
3 - 2
3 =
x
x
3 + 16
3 - 2
(3x
2)2
= 3(3x
+ 16)
(3x
)2
4(3x
) + 4 = 3(3x
) + 48
(3x
)2
4(3x
) + 4 3(3x
) 48= 0
(3x
)2
4(3x
) 3(3x
) 44 = 0
(3x
)2
7(3x
) 44 = 0
(3x
11)(3x
+ 4) = 0
F F 3x
11 = 0 (3x
+ 4 F F F)
x = log311
3 F Fก F (log93) = 1
2 , 1, 3
2
ก ก Sn = n
2 [2a1 + (n 1)d]
F n = 4, a1 = 1
2 F S4 = 4
2 [2( 1
2 ) + (4 1) 1
2 ] = 2[1 + 3
2 ] = 5
3S
= 35
= 243
F 4.9 x F ก ก
log 2x
log 3 + log3(x 12) = ( )3log x x + 5 - x - 5
F F ก F
กF F ก F ก F F ก ก F F ก กF](https://image.slidesharecdn.com/lecture005-relationsfunction-140713074949-phpapp02/75/relations-function-66-2048.jpg)
![F F 59
log3 2x + log3(x 12) = 2 log3 ( )x x + 5 - x - 5
log3 [2x(x 12)] = log3 ( )
2
x x + 5 - x - 5
2x(x 12) = ( )
2
x x + 5 - x - 5
2x(x 12) = x[(x + 5) + (x 5) 2( x + 5 )( x - 5 )]
2x(x 12) = x[2x 2( x + 5 )( x - 5 )]
2x2
24x = 2x2
2x( x + 5 )( x - 5 )
24x = 2x( x + 5 )( x - 5 )
กก F ก F F
576x2
= 4x2
(x2
25)
= 4x4
100x2
4x4
676x2
= 0
4x2
(x2
169) = 0
กF ก F x = 0 x2
= 169
x = 0 x = 13 x = 13
F F x = 0 x = 13 F ก ˈ
ก x = 13
4.6.2 ก ก
ก กF ก ก กก F ก ก กF ก ก ก F ก F
ก F ก ก ก ก กก F F ˆ กF ก
ก F ˈ ˆ กF ก F ˈ F ก ก ก F F ˈ ˆ กF F
ก ก F ก F F
F 4.10 ก F A ˈ ก log4log3log2(x2
+ 2x) ≤ 0 ˈ ก
A ก
ก ก log4log3log2(x2
+ 2x) ≤ 0
F F log3log2(x2
+ 2x) ≤ 1 (4 > 0 ˈ ˆ กF )
log2(x2
+ 2x) ≤ 3 (3 > 0 ˈ ˆ กF )
x2
+ 2x ≤ 8 (2 > 0 ˈ ˆ กF )
x2
+ 2x 8 ≤ 0
(x 2)(x + 4) 0
F F 4 ≤ x ≤ 2 ˈ F F F [ 4, 2]](https://image.slidesharecdn.com/lecture005-relationsfunction-140713074949-phpapp02/75/relations-function-67-2048.jpg)
![60 F ˆ กF
F ก x2
+ 2x > 0 F F x(x + 2) > 0
( ∞, 2) ∪ (0, ∞)
ก A = [ 4, 2] ∩ [( ∞, 2) ∪ (0, ∞)] = [ 4, 2) ∪ (0, 2]
F F ˈ ก A F กF { 4, 3, 1, 2} 4](https://image.slidesharecdn.com/lecture005-relationsfunction-140713074949-phpapp02/75/relations-function-68-2048.jpg)


