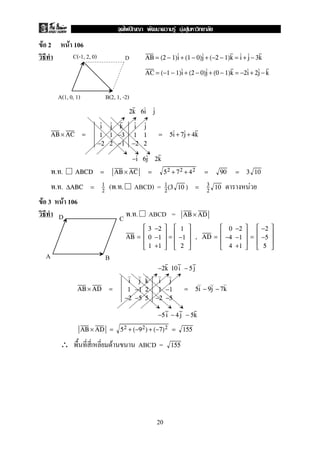
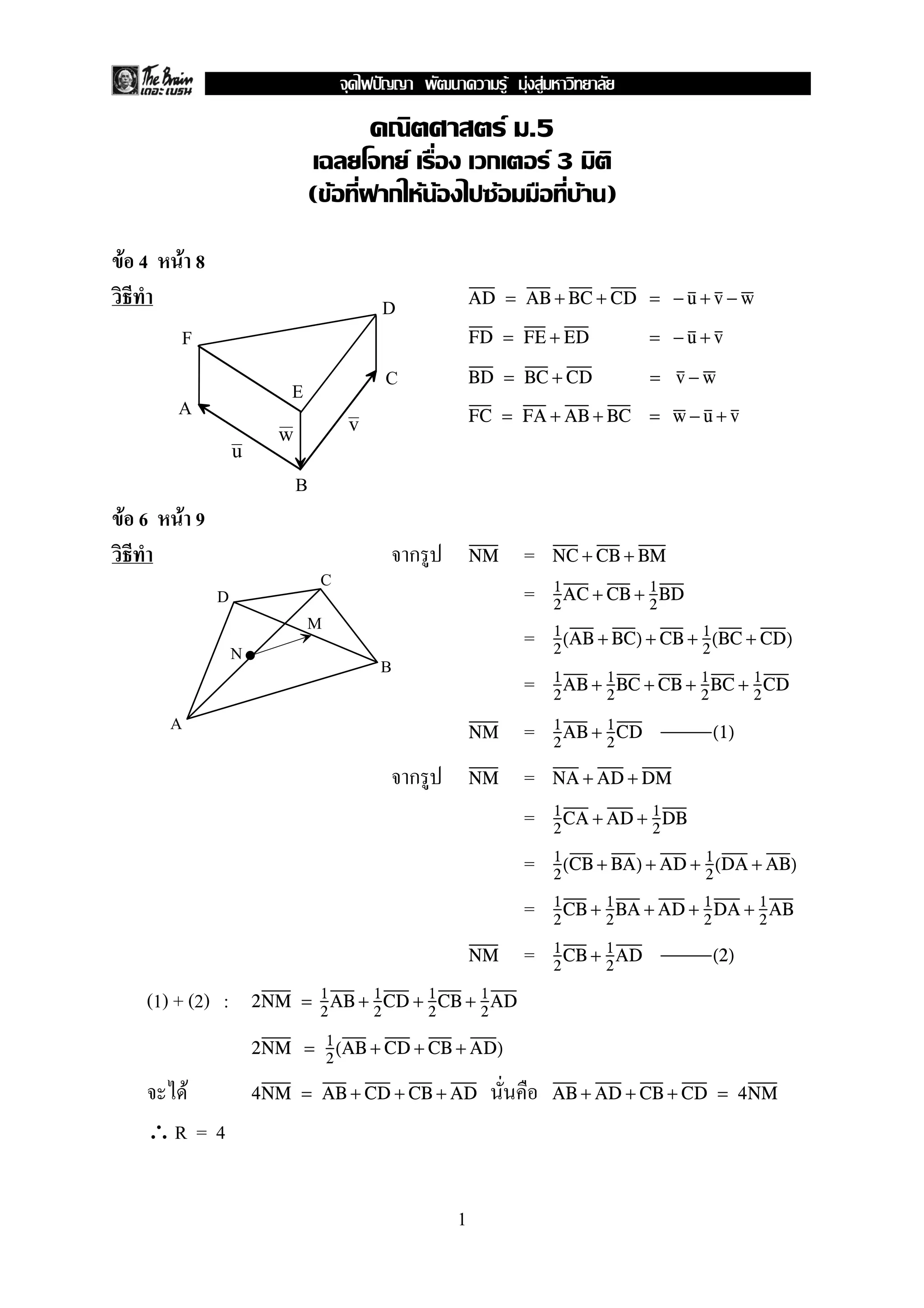
1. The document contains equations relating variables u, v, w, x, and expressions involving i and j. 2. Key steps show that r = 4, s = 2, and the expression for w is w = 2u - 3v. 3. Another part derives expressions for m and n in terms of another variable, finding m = 3/5, n = 2/7.

1. F .5
F ก F 3
( F ก F F F F )
F 4 F 8
AD = AB + BC + CD = − u + v − w
FD = FE + ED = − u + v
BD = BC + CD = v − w
FC = FA + AB + BC = w − u + v
F 6 F 9
ก =NM NC + CB + BM
= 1
2
AC + CB + 1
2
BD
= 1
2
(AB + BC) + CB + 1
2
(BC + CD)
= 1
2
AB + 1
2
BC + CB + 1
2
BC + 1
2
CD
=NM 1
2
AB + 1
2
CD (1)
ก =NM NA + AD + DM
= 1
2
CA + AD + 1
2
DB
= 1
2
(CB + BA) + AD + 1
2
(DA + AB)
= 1
2
CB + 1
2
BA + AD + 1
2
DA + 1
2
AB
=NM 1
2
CB + 1
2
AD (2)
(1) + (2) : 2NM = 1
2
AB + 1
2
CD + 1
2
CB + 1
2
AD
2NM = 1
2
(AB + CD + CB + AD)
F 4NM = AB + CD + CB + AD AB + AD + CB + CD = 4NM
∴R = 4
A
B
C
D
E
F
v
u
w
A
B
C
D
N
M
1
ˆ F F F

2. F 3 F 10
กก cosine
b2 = a2 + c2 − 2accos 60
b2 = 102 + 52 − 100

1
2

 = 75
b = 75 = 5 3 km
กก :θ cos ine a2 = b2 + c2 − 2bc cos θ
52 = (5 3 )2 + 102 − 2(5 3 )(10)cos θ
cos θ =
3
2
→ θ = 30
∴ F F ก F ˈ 5 3 km 060
F 5 F 14 2
ก =AH AF + FH
= 2FD + 1
2
CF
= 2u + 1
2
v
F 6 F 15 * กF F กF ˈ *OC OE
F 8 F 15 1
ก u = AB + BM (1)
v = 1
3
AB + 5BM (2)
(1) × 5 : 5u = 5AB + 5BM (3)
(3) − (2) : 5u − v = 14
3
AB
AB = 3
14
(5u − v)
AB = 15u
14
− 3v
14
B
A
C
a = 5 km
b
c=10km30 + 0 = 60
30
150
30 30
0
B D C
A
EH F
2
22
1 1
1
AH
D
A B
CN1 2
4
1
v
u
5BM
AB1
3
M
2
ˆ F F F

3. F 9 F 16
ก =EF EC + CF
= 2
3
u + (−1
3
)(u + v)
= 2
3
u − 1
3
u − 1
3
v
= 1
3
u − 1
3
v
=EF 1
3
(u − v)
F 11 F 16
ก =BF AF − AB
= 1
2
AE − u = 1
2

v + 1
2
u
 − u
= 1
2
v + 1
4
u − u = 1
2
v − 3
4
u
F 13 F 17
ก F F∆AFD ∼ ∆BFE
ˈ 2 F∆AFD ∆BFE
ก F =AF 1
3
(AD + 2AB) = 1
3
(u + 2v)
= 1
3
u + 2
3
v
F 14 F 17 2
ก ∆AEF ∼ ∆CDF
FAE = 3DC CF = 3FA
AD = 3
2
a − 4b
2
2
1
1
C
E
F
v
EF
u
u+v
D
A B
C
F
E
D C
BA
F E
v
u 2
1
D C
BA
F
E1 2
b
a
a3
2
a1
2
3b
3
ˆ F F F

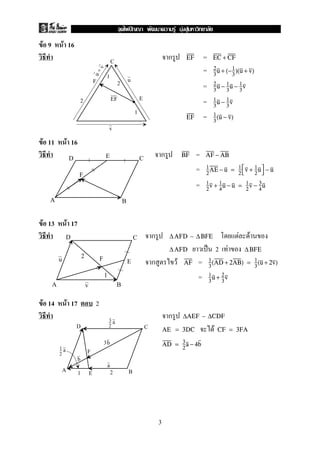
4. F 4 F 18 2
AF = mAP → BF = nBQ
=AF mAP
= m(AB + BP)
= m(AB + 4
7
BC)
=AF mAB + 4
7
mBC..........(1)
= = = =BF nBQ n(BC + CQ) n(BC + 4
9
CD) n [ BC + 4
9
(−AB)]
= = =BF nBC − 4
9
nAB → −FB nBC − 4
9
nAB → FB 4
9
nAB − nBC .......(2)
=(1) + (2) ; AF + FB mAB + 4
7
mBC + 4
9
nAB − nBC
=AB mAB + 4
7
mBC + 4
9
nAB − nBC
=AB − mAB − 4
9
nAB 4
7
mBC − nBC → AB(1 − m − 4
9
n) = BC(4
7
m − n)
ก ∴ ก ˈAB //BC 1 − m − 4
9
n = 0 4
7
m − n = 0
กF ก F ∴m = 63
79
n = 36
79
m + n = 99
79
F 16 F 19 9
∆ABC
ก F F
BD = 1
3 +1
(1BC + 3BA)
BD = 1
4
BC − 3
4
AB
ก DF = BF − BD = 1
3
BC − 

1
4
BC − 3
4
AB
 = 3
4
AB + 1
12
BC
∴ a
b
=
3
4
1
12
= 9
B C
A D
F
Q
4
5
4 3P
3
1 1
2
C
A B
F
BF = BC1
3
a a
4
ˆ F F F

5. F 1 F 23 2
=2
5
u + (6 − 3x2)v 100u + 2
3
v
=(2
5
− 100)u (2
3
− 6 + 3x2)v
=u (3x2 − 16
3
)
(2
5
− 100)
v
ก F ˈ2
5
− 100 3x2 − 16
3
< 0
3 ก F x2 − 16
9
< 0
x2 − 

4
3


2
< 0
(x − 4
3
)(x + 4
3
) < 0 x ∈ (−4
3
, 4
3
)
F 3 F 24 3
ก F =x2v − xv 2u
=(x2 − x)v 2u → u =
(x2 −x)
2
v
ก ก F ก F Fu v
x2 −x
2
< 0 → x2 − x < 0 → x(x − 1) < 0
F F ˈ 0 < x < 1
F 5 F 24 3
1. au + v = 3v − u → au + u = 2v → (a + 1)u = 2v
F F F ก F กu v
2. 3u − 2v = 4v − 2u → su = 6v → u = 6
5
v
∴ ก กu v
3. 3
2
v = v − u → 1
2
v = − u → v = − 2u
∴ ก F กu v
4. ∴ ก ก2v = u + v → u = v u v
F ˈ ก
u ก v ก
3
4
3
4
0 1
5
ˆ F F F

6. F 1 F 25
8x + r(y − x) = 2s(y + x)
8x + ry − rx = 2sy + 2sx
8x − rx − 2sx = 2sy − ry
(8 − r − 2s)x = (2s − r)y
// F Fx y 8 − r − 2s = 0 − (1) 2s − r = 0 − (2)
กF ก (1) (2) F r = 4 s = 2 ∴ rs = (4)(2) = 8
F 5 F 27
=ZB mYB = m(AB − 2
5
v) = mu − m2
5
v ..........(1)
=ZB XB − XZ = 3
5
u − nXC = 3
5
u − n(AC − AX) = 3
5
u − n(v − 2
5
u)
= 3
5
u − nv + n2
5
u = (3
5
+ 2
5
n)u − nv ..........(2)
(1) = (2) : mu − m2
5
v = 

3
5
+ 2
5
n
 u − nv
F m = 3
5
+ 2
5
n ..........(3) m2
5
= n ..........(4)
F n ก (4) (3) F m = 3
5
+ 2
5
(m2
5
) → m = 5
7
F m (4) F n = 2
7
F m n (1) F ZB = 5
7
u − 2
7
v
F 1 F 28 3
F =w au + bv ..........(1)
=−7i − 14j a(i − 4j) + b(3i + 2j) = ai − 4aj + 3bi + 2bj = (a + 3b)i + (2b − 4a)j
=a + 3b −7 2b − 4a = − 14
กF ก F ∴a = 2 , b = − 3 w = 2u − 3v
X
A
YZ
B C
6
ˆ F F F

7. F 3 F 29
=w mu + nv
=−14i + 14j m(2i + 3j) + n(4i − j)
= 2mi + 3mj + 4ni − nj
=−14i + 14j (2m + 4n)i + (3m − n)j
F 2m + 4n = − 14 ..........(1) 3m − n = 14 ..........(2)
กF ก (1) (2) F m = 3 n = − 5
∴ m2 + n2 − 25 = 32 + (−5)2 − 25 = 3
F 3 F 34
ก ก F 3i − 4j −4
3
F กก 3i − 4j 3
4
ก F F กก(−2,1) 3i − 4j
F ˈy − 1 = 3
4
(x − (−2)) 4x + 3y + 5 = 0
F 4 F 35 4
F u = 2i − 3j mu = − 3
2
m u = 2
3
ก F F กก(2,−2) u
F ˈy − (−2) = 2
3
(x − 2) 2x − 3y − 10 = 0
F 6 F 35 3
AC = AB + AD
AC = (2i + 3j) + (5i − 2j)
AC = 7i + j
AC = 72 + 12 = 50 = 5 2
D
A
C
B
5i-2j
2i + 3j
7
ˆ F F F

8. F 10 F 37 3
ก F∆ABC
CD = 1
2 +3
2(3i − 2j) + 3(2i + 3j)
CD = 1
5
6i − 4j + 6i − 9j
CD = 1
5
12i + 5j
CD = 1
5
122 + 52 = 1
5
(13) = 13
5
F 11 F 37 1
ก F∆AOB
=OC 1
3
3i − 2j + 2(2i + 5j)
= 1
3
3i − 2j + 4i + 10j
=OC 1
3
7i + 8j
= ∴OC 1
3
113 OC
2
= 113
9
F 9 F 42 3
F ก F 1 F กกu = i + 2j u ±
(2i−j)
5
ก ˈ ก F F กกAB 5 u
AB =
± 5 (2i −j)
5
= ± (2i − j) = ±



2
−1


 (1)
ก F A(1, 0) F B ก (x, y) F AB =



x −1
y −0


 (2)
(1) = (2) : ±



2
−1


 =



x −1
y − 0



กF ก F (x, y) 2 (−1,1) (3,−1)
D
A
CB 2i + 3j
3i - 2j
3
2
A
O B
C
2
1
2i + 5j
3i-2j
8
ˆ F F F

9. F 10 F 42
F F (0, 0) FCA =



−7
14


 A(−7,14)
F (0, 0) FCB =





0
−35
3





B(0,−35
3
)
=CD CA + AD
= CA + 3
7
AB
= CA + 3
7
(CB − CA)
= 4
7
CA + 3
7
CB
= 4
7
(−7i + 14j) + 3
7
(0i − 35
3
j)
=CD −4i + 3j
ก F 1 F ก =CD CD
CD
= −
4i +3j
5
= − 4
5
i + 3
5
j
F 6 F 49
F w = ai + bj
u ⋅ w = − 11 → 2a − 5b = − 11 (1)
v ⋅ w = 8 → 1a + 2b = 8 (2)
(2) × 2 : 2a + 4b = 16 (3)
(3) − (1) : 9b = 27 → b = 3
F b (2) F a = 2 ∴ w = 2i + 3j
w = 22 + 32 = 13
ก =w ⋅ (5i + j) w 5i + j cos θ
=(2i + 3j) ⋅ (5i + j) 13 26 cos θ
=cos θ 1
2
→ θ = 45
∴tan θ + sin 2θ = tan 45 + sin 2(45 ) = 1 + 1 = 2
A(-7,14)
C(0,0)
D(a,b)
4
3
B(0,- )35
3
9
ˆ F F F

10. F 12 F 51 1
ก. ก F กก Fu v u ⋅ v = 0
ก F กก Fu + v u − v (u + v) ⋅ (u − v) = 0
F F ก. ก→ u 2 − v 2 = 0 u = v
= 0 u = v
. . ก(u + 2v) ⋅ (2u − 2v) = 2 u 2 + 3u ⋅ v − 2 v 2 = 0
F 13 F 52
ก Fu i − 2j mu = 1
2
m = − 2
ˈ ก b > 0 F ˈu 2i + j −2i − j u = ai + bj u 2i + j
F ก ก F dot กu i + j
F =u ⋅ (i + j) u i + j cos θ
=(2i + j) ⋅ (i + j) 2i + j i + j cos θ
=2(1) + 1(1) 5 2 cos θ
=cos θ 3
10
ก F∆ tan θ = 1
3
∴9 tan θ = 9

1
3

 = 3
F 14 F 52 2
ก F = 3 Fb a b a ⋅ b = 0
= 3(−2p)2
+ 22 + p2 (1)(−2p) + 

1
2

 (2) + (−3p)(p) = 0
= 35p2 + 4 −2p + 1 − 3p2 = 0 (1)
= 1 F (1) Fp2 p2
−2p + 1 − 3(1) = 0 → p = − 1
∴ F p F a b b = 3
F F−1 (−3
2
,0)
= 0
1
3
10
0
10
ˆ F F F

11. F 18 F 54 2
=u + v 2 + u − v 2 2 u 2 + 2 v 2
=37 + 13 2( u 2 + v 2)
=u 2 + v 2 25 (1)
=u + v 2 − u − v 2 4u ⋅ v
=37 − 13 4 u v cos 60
=2 u v 24 (2)
(1) + (2) : = 25 + 24u 2 + 2 u v + v 2
= 49( u + v )2
= 7u + v
F 23 F 56 2
ก F = ก F x + 5y = 21u − v 2 u 2 + v 2
= = 21u − 2u ⋅ v + v 2 u 2 + v 2 5y
4
+ 5y
= 0 y =−2u ⋅ v 12
5
= 0 F y (1) Fu ⋅ v
= 04x − 3y x = 3
4


12
5

 = 9
5
x = 3y
4
(1) u = xi + yj = 9
5
i + 12
5
j
∴ u ⋅ w = 9
5
(2) + 12
5
(1) = 6
F 28 F 59
u + 4v = 3v − 2w → u = − v − 2w (1) : (1) × 3 : 3u = − 3v − 6w (3)
4u − 2w = 3v + 2w → 4 u = 3v + 4w (2) : (1) × 4 : 4u = − 4v − 8w (4)
(2) + (3) : 7u = − 2w → 7u = − 2w → 7 u = 2 w → 7 u = 2(14) → u = 4
(2) = (4) : 3v + 4w = − 4v − 8w → 7v = − 12w → 7v = − 12w → 7 v = 12 w
∴→ 7 v = 12(14) → v = 24 v 2 − w 2 + u 2 = 242 − 142 + 42 = 396
1
2
11
ˆ F F F

12. F 31 F 61
a + b + c 2 = a 2 + b 2 + c 2 + 2a ⋅ b + 2b ⋅ c + 2c ⋅ a = 0 (1)
F (1) Fa + c 2 = − b 2 a , b c
a + b + c = 0 10 = b 2 9 + 10 + 25 + 2(a ⋅ b + b ⋅ c + c ⋅ a) = 0
a + b 2 = − c 2 a ⋅ b + b ⋅ c + c ⋅ a = − 22
25 = c 2
F 32 F 61 3
1. (u ⋅ v)2 = u 2 v cos2θ = (u ⋅ u)(v ⋅ v)cos2θ
ก 0 ≤ cos2θ ≤ 1
(u ⋅ v)2 ≤ (u ⋅ u)(v ⋅ v)
2. F u ≠ 0 , v ≠ 0 u v
F u ⋅ v = 0 → (u ⋅ v)2 = 0
F ( u v )2 ≠ 0
∴ (u ⋅ v)2 ≠ ( u v )2
3. ก =u + v + w 0
=u + v w
=u + v 2 w 2
=u 2 + 2u ⋅ v + v 2 w 2
=32 + 2u ⋅ v + 42 72
= 12u ⋅ v
4. =u − v 2 u 2 − 2u ⋅ v + v 2
F F F ก F u v
F F F u − v 2 = u 2 + v 2
12
ˆ F F F

13. F 2 F 79
F 2 F 82
ก F AB =





−2 − 1
3 − 2
1 − 0





=





−3
1
1





, AB = (−3)2 + 12 + 12 = 11
ก F 3 F F AB −3 AB
AB
= −3
11





−3
1
1





F 3 F 85 1
ก F r4 = ar1 + br2 + cr3





3
2
5





= a





2
−1
1





+ b





1
3
−2





+ c





−2
1
−3





F F 3 = 2a + b − 2c (1)
2 = − a + 3b + c (2)
5 = a − 2b − 3c (3)
:(2) × 2 4 = − 2a + 6b + 2c (4)
:(1) + (4) 7 = 7b → b = 1
b (2) : 2 = − a + 3(1) + c → − 1 = − a + c (5)
b (3) : 5 = a − 2(1) − 3c → 7 = a − 3c (6)
:(5) + (6) 6 = − 2c → c = − 3
c (6) : 7 = a − 3(−3) → a = − 2
∴ a + b + c = (−2) + 1 + (−3) = − 4
4
31
y
x
z
P(1, 3, 4)
13
ˆ F F F

14. F 2 F 87
a + c =





2 + d
4 + d + 1
−5 + d + 2





=





d + 2
d + 5
d − 3





b =





3
6
−2





F F กF F3
d +2
= 6
d +5
= −2
d−3
d = 1
∴ c =





1
2
3





c = 12 + 22 + 32 = 14
F 3 F 88
ก F Fu ⋅ v = 2 1a + 2b + 3c = 2 (1)
ก w = ai + bj + ck // − 2
3
i + 1
2
j + 1
3
k
F a
− 2
3
= b
1
2
= c
1
3
→ − 3
2
a = 2b = 3c (2)
F 2b , 3c ก (2) (1) F
1a + 
−3
2
a
 + 
−3
2
a
 = 2 → a = − 1
F a (2) F 3
2
= 2b = 3c → b = 3
4
, c = 1
2
∴a + 4b + 2c = − 1 + 4

3
4

 + 2

1
2

 = 3
F 2 F 90
AB =





2 −1
0 −2
−3 +1





=





1
−2
−2





, AB = 12 + (−2)2 + (−2)2 = 3
F ก F AB 1
3
, −2
3
, −2
3
F 3 F 93
= = , = =AB (3 + 1)i + (1 − 2)j + (−2 − 1)k 4i − j − 3k AB 42 + (−1)2 + (−3)2 26
= = , = =AC (5 + 1)i + (3 − 2)j + (−2 − 1)k 6i + j − 3k AC 62 + 12 + (−3)2 46
= = 32AB ⋅ AC (4)(6) + (−1)(1) + (−3)(−3)
ก = 32 =AB ⋅ AC AB AC cos θ → 26 ⋅ 46 cos θ
= = =cos θ 16
13 23
16
299
→ θ cos−1 16
299
14
ˆ F F F

15. F 5 F 94
ก F F กก F dot ก F F ˈ F
ก F , ,u = i − 2j + 5k v = 7i − 2j + 2k w = 2i − 3j + 4k
∴ ก F กกu ⋅ v = (1)(7) + (−2)(−2) + (5)(2) = 21 u v
∴ ก F กกu ⋅ w = (1)(2) + (−2)(3) + (5)(−4) = -24 u w
∴ ก กกv ⋅ w = (7)(2) + (−2)(3) + (2)(−4) = 0 u w
F 8 F 94
ก A, B C ˈ ก
A(4,9,1),B(−2,6,3) C(6,3,−2)
F AB = (−2 − 4)i + (6 − 9)j + (3 − 1)k = − 6i − 3j + 2k
BC = (6 + 2)i + (3 − 6)j + (−2 − 3)k = 8i − 3j − 5k
AC = (6 − 4)i + (3 − 9)j + (−2 − 1)k = 2i − 6j − 3k
ก ˈ ก F F ก F 1 F กก∆ABC ∆
(dot ก F F 0) ก ก ˈ ก F ก F F∆
dot ก
AB ⋅ BC = (−6)(8) + (−3)(−3) + (2)(−5) = − 49 ≠ 0
AB ⋅ AC = (−6)(2) + (−3)(−6) + (2)(−3) = 0
BC ⋅ AC = (8)(2) + (−3)(−6) + (−5)(−3) = 49 ≠ 0
กก dot ก F F ก F 1 F dot ก F F F F F ∆
กก ∴ ˈ ก∆ABC ∆
F 10 F 95
BC = (−1 − 2)i + (−6 + 1)j + (4 + 4)k = 3i − 5j + 8k
BC = (−3)2 + (−5)2 + 82 = 98 = 7 2
BA = (5 − 2)i + (−3 + 1)j + (2 + 4)k = 3i − 2j + 6k
BA = 32 + (−2)2 + 62 = 7
BA ⋅ BC = BA BC cos θ
(3)(−3) + (−2)(−5) + (6)(8) = (7)(7 2 )cos θ → cos θ = 1
2
→ θ = 45
A(5, -3, 2)
B(2, -1, -4) C(-1, -6, 4)
15
ˆ F F F

16. F 2 F 98
= , =AB





1 − 3
0 − 1
−1 − 2





=





−2
−1
−3





AC





−2 − 3
2 − 1
3 − 2





=





−5
1
1





−5k 3i 2j
= =AB × AC
i j k
−2 −1 −3
−5 1 1
i j
−2 −1
−5 1
2i + 13j − 7k
− i + 15j − 2k
F 1 F 100
ก) ก F ก F F F ˈ ก F(u × v) × w ×
ก F ก F
) ก F ก F F F(u ⋅ v) × w ×
ก F ก F
) ก F ก F F F ˈ ก Fu ⋅ (v × w) ⋅
ก F ก F
) ก F ก F F F ˈ ก Fu × (v × w) ×
ก F ก F
F 2 F 100 1
1. ก (u × v) ⋅ w = u ⋅ (v × w)
2. (u × v) × w ≠ u × (v × w)
3. u ⋅ (v × w) = (u × v) ⋅ w
F u ⋅ (v × w) ≠ (u × v) ⋅ (u × w)
4. u × (v × w) ≠ (u × v) × (u × w)
16
ˆ F F F

17. F 3 F 100 3
1. ก กก FA × B A A ⋅ (A × B) = 0
2. ก =(A − B) × (A + B) A × A + A × B − B × A − B × B
= A × B + A × B = 2(A × B) = (2A) × B
3. =(A − B) × (A − B) A × A − A × B − B × A + B × B
= B × A − B × A = 0
4. ก F กF CROSS(A + B) ⋅ (A − B) × (A × B)
VECTOR VECTOR VECTOR
ก กF F F dot ก F กF CROSS ก F F
ˈ VECTOR dot F ก F F F ˈ SCALAR
F 4 F 101 4
1. ก
2. ก : u ⋅ (v × r) = (u × v) ⋅ r = − (v × u) ⋅ r = − r ⋅ (v × u)
3. ก : F Fu = r v ⋅ (r × u) = v ⋅ (u × u) = v ⋅ 0 = 0
F 5 F 101 1
ก. ก ก F F F F a + b + c = 0
b × c = b × (−a − b) = − b × a − b × b = a × b
c × a = c × (−b − c) = − c × b − c × c = b × c
∴ a × b = b × c = c × a
. F F Fa × b = a × c b = c
F 6 F 101 2
a ⋅ x = a ⋅ b ×c
a ⋅b× c
= a ⋅b ×c
a ⋅b ×c
= 1 a ⋅ x + 2b ⋅ y + 3c ⋅ z = 2
2b ⋅ y = 2b ⋅ a× c
a⋅ b×c
= − 2a⋅ b×c
a⋅ b×c
= − 2
3c ⋅ z = 3c⋅ a× b
a⋅ b×c
= 3a ⋅b× c
a ⋅b× c
= 3
oo
o o
o
o
A C
B
a b
c
17
ˆ F F F

18. F 7 F 102
1 : u = 2i − j + 0k → u = 22 + (−1)2 + 02 = 5
v = 2i + j + k → v = 22 + 12 + 12 = 6
=u × v =
i j k
2 −1 0
2 1 1
i j
2 −1
2 1
= − i − 2j + 4k u × v = (−1)2 + (−2)2 + 42 = 21
ก u × v = u v sin θ → 21 = 5 ⋅ 6 sin θ → sin θ = 21
30
2 ก u ⋅ v = u v cos θ
=(2)(2) + (−1)(1) + (0)(1) 5 6 cos θ
=cos θ 3
30
ก sin θ = 21
30
F 9 F 103
u ⋅ v = 2(−1) + (−1)(1) + 1(−2) = − 5 u ⋅ v = 5
u × v =





2
−1
1





×





−1
1
−2





=





1
3
1





u × v = 12 + 32 + 12 = 11
ก F F ก กก ก Fu ⋅ v
u v ± u ⋅ v
(u ×v)
u ×v
= ± 5
11





1
3
1





F 10 F 103
w × v =





a
b
c





×





1
0
3





=





3b
c − 2a
−b





=





−15
−17
5





F b = − 5 c − 3a = − 17 (1)
ก u w: u ⋅ w = 0 → a + 2b + 4c = 0 → a + 2(−5) + 4c = 0
→ a + 4c = 10 (2)
(2) × 3 : 3a + 12c = 30 (3)
∴(1) + (3) : 13c = 13 → c = 1 b + c = − 5 + 1 = − 4
+2k +0 - 2j
-i + 0 + 2k
3
21
30
0
18
ˆ F F F

19. F 11 F 104 1
AB × AC = AB AC sin θ
AB ×AC
AB
= AC sin θ (1)
ก F AB =





6 − 2
5 − 2
2 − 2





=





4
3
0





, AC =





−4 − 2
0 − 2
−3 − 2





=





−6
−2
−5





AB × AC =





4
3
0





×





−6
−2
−5





=





−15
20
10





= 5





−3
4
2





AB = 42 + 32 + 02 = 25 , AB × AC = 5 (−3)2 + 42 + 22 = 5 29
ก sin θ = CD
AC
→ CD = AC sin θ = AB× AC
AB
=
5 29
5
= 29
F 12 F 104 1
F (1) Fu ⋅ v = u v cos θ a2
3a2 − 3b2 = 3 4a2 + 9b2 

1
3

 2(5 − b2) − 3b2 = 4(5 − b2) + 9b2
3a2 − 3b2 = 4a2 + 9b2 (1) 10 − 5b2 = 20 + 5b2
ก = 3 กก ˆˉ Fu
= 3a2 + b2 + 22
100 − 100b2 + 25b4 = 20 + 5b2
= 5a2 + b2 25b4 − 105b2 + 80 = 0
=a2 5 − b2 (2) 25(b2)2 − 105b2 + 80 = 0
กF ก F b = 1, 3.2
F b (2) F a2 = 5 − 12 = 4 → a = 2
u × v =





a
b
2





×





2a
−3b
−5ab





=





6b
4a
−5ab





=





6
8
−10





C(-4, 0,-3)
A(2, 2, 2) B(6, 5, 2)
0
D
19
ˆ F F F

20. F 2 F 106
AB = (2 − 1)i + (1 − 0)j + (−2 − 1)k = i + j − 3k
AC = (−1 − 1)i + (2 − 0)j + (0 − 1)k = −2i + 2j − k
2k 6i j
AB × AC =
i j k
1 1 −3
−2 2 −1
i j
1 1
−2 2
= 5i + 7j + 4k
−i 6j 2k
. . ABCD = AB × AC = 52 + 72 + 42 = 90 = 3 10
. . ( . . ABCD) = F∆ABC = 1
2
1
2
(3 10 ) = 3
2
10
F 3 F 106
. . ABCD = AB × AD
AB =





3 −2
0 −1
1 +1





=





1
−1
2





, AD =





0 −2
−4 −1
4 +1





=





−2
−5
5





−2k 10 i − 5 j
AB × AD =
i j k
1 −1 2
−2 −5 5
i j
1 −1
−2 −5
= 5i − 9j − 7k
−5 i − 4 j − 5k
AB × AD = 52 + (−92) + (−7)2 = 155
∴ F ABCD = 155
C(-1, 2, 0) D
A(1, 0, 1) B(2, 1, -2)
A B
CD
20
ˆ F F F

21. F 4 F 106 2
= 3 = 2u ⋅ v
= 3 = 2u v cos θ u × v
= 3 = 21 v cos θ u v sin θ
= =v 2cos2θ 9 (1) u 2 v 2sin2θ 4 (2)
(1) + (2) : = 9 + 4v 2cos2θ + v 2sin2θ
= 13v 2(cos2θ + sin2θ)
= 13v 2(1)
= 13v 2
F 2 F 108
F u = AB =





−1 −1
0 −2
2 +1





=





−2
−2
3





v = AC =





2 −1
3 −2
4 +1





=





1
1
5





r = AD =





0 −1
−1 −2
2 +1





=





−1
−3
3





F (u × v) ⋅ w
=
−2 −2 3
1 1 5
−1 −3 3
−2 −2
1 1
−1 3
= − 26
∴ F ก F− 26 = 26
*************************
D
A
B
C
v
u
r
-6 10 -9
3 -30 6
21
ˆ F F F