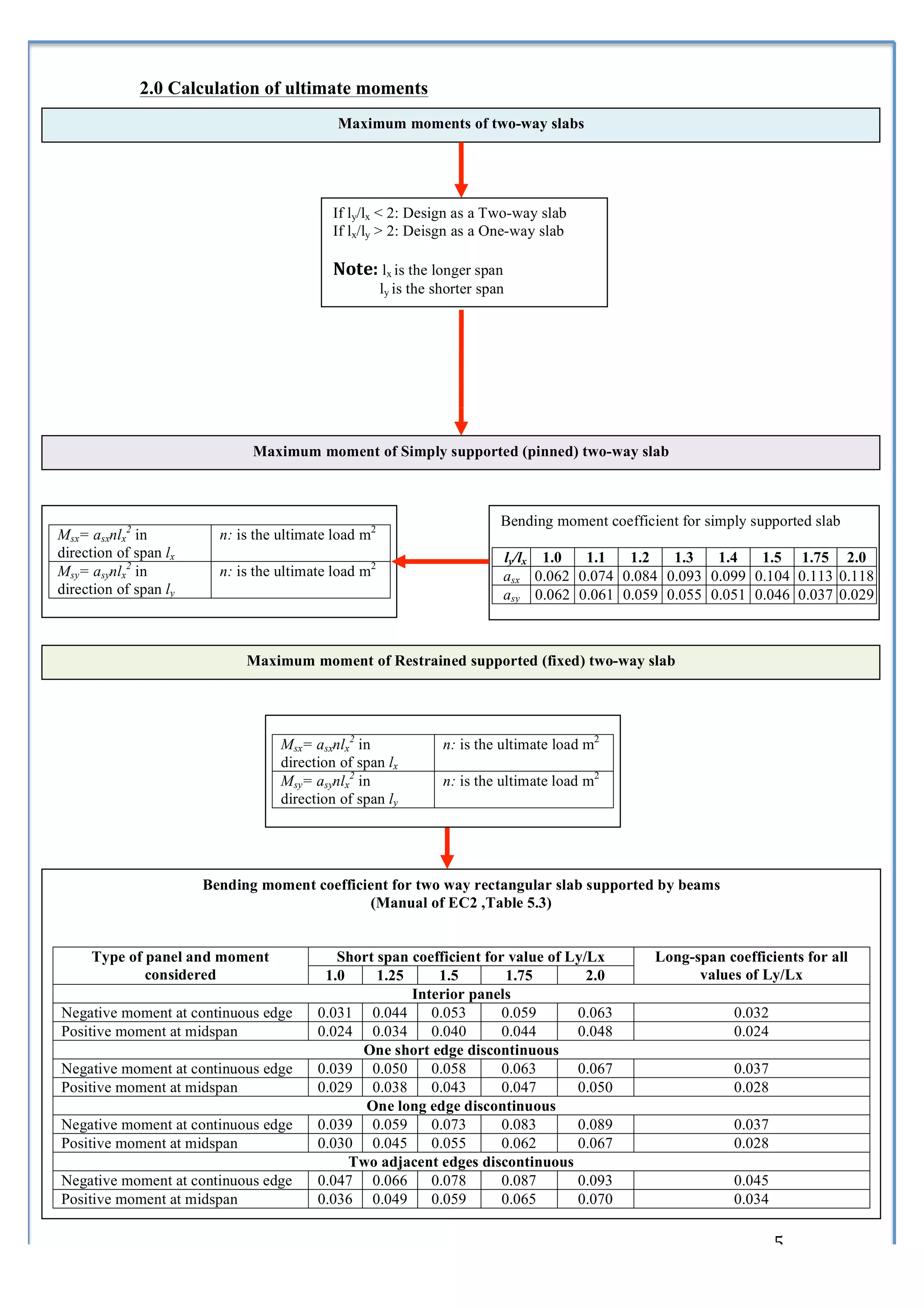
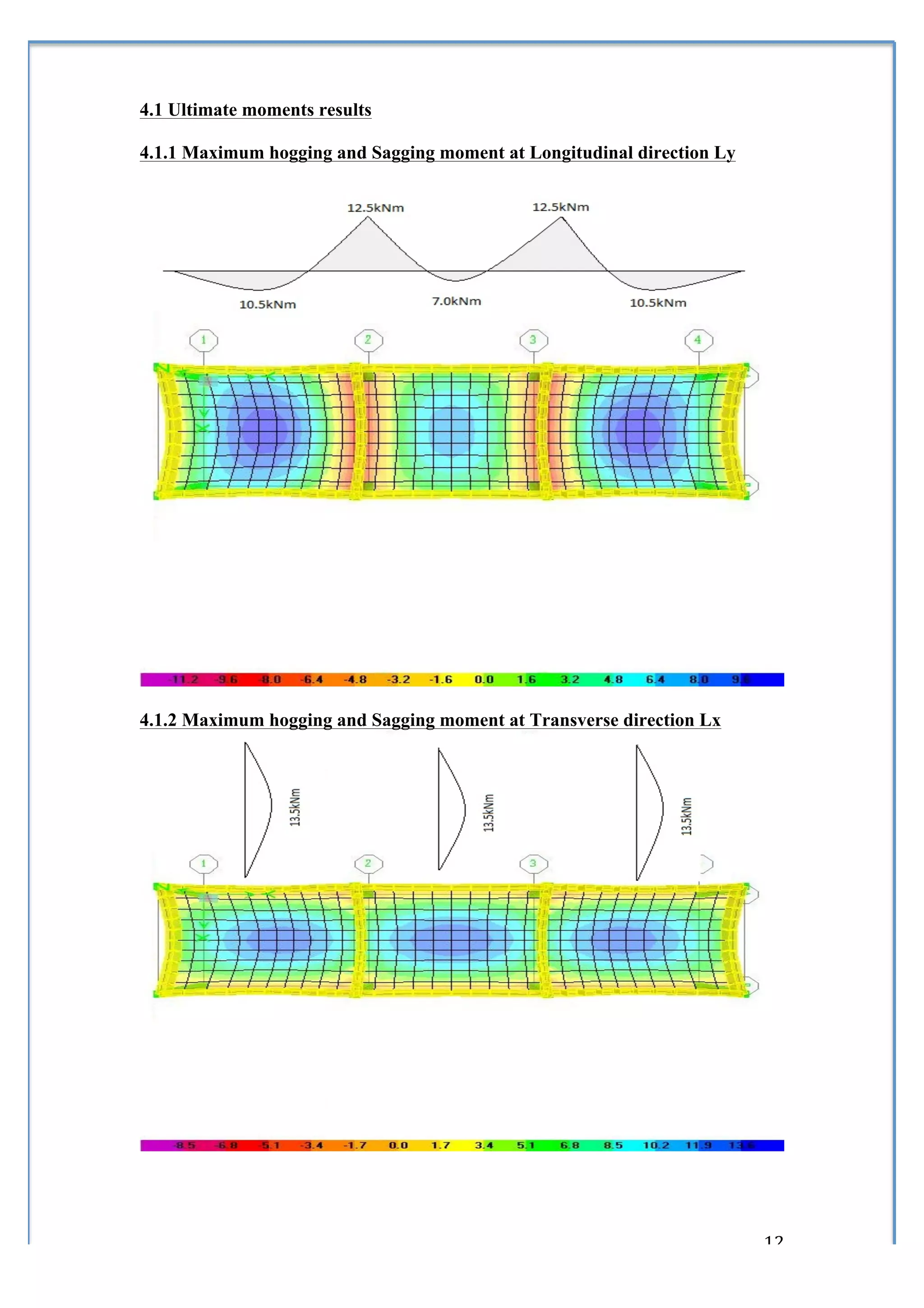
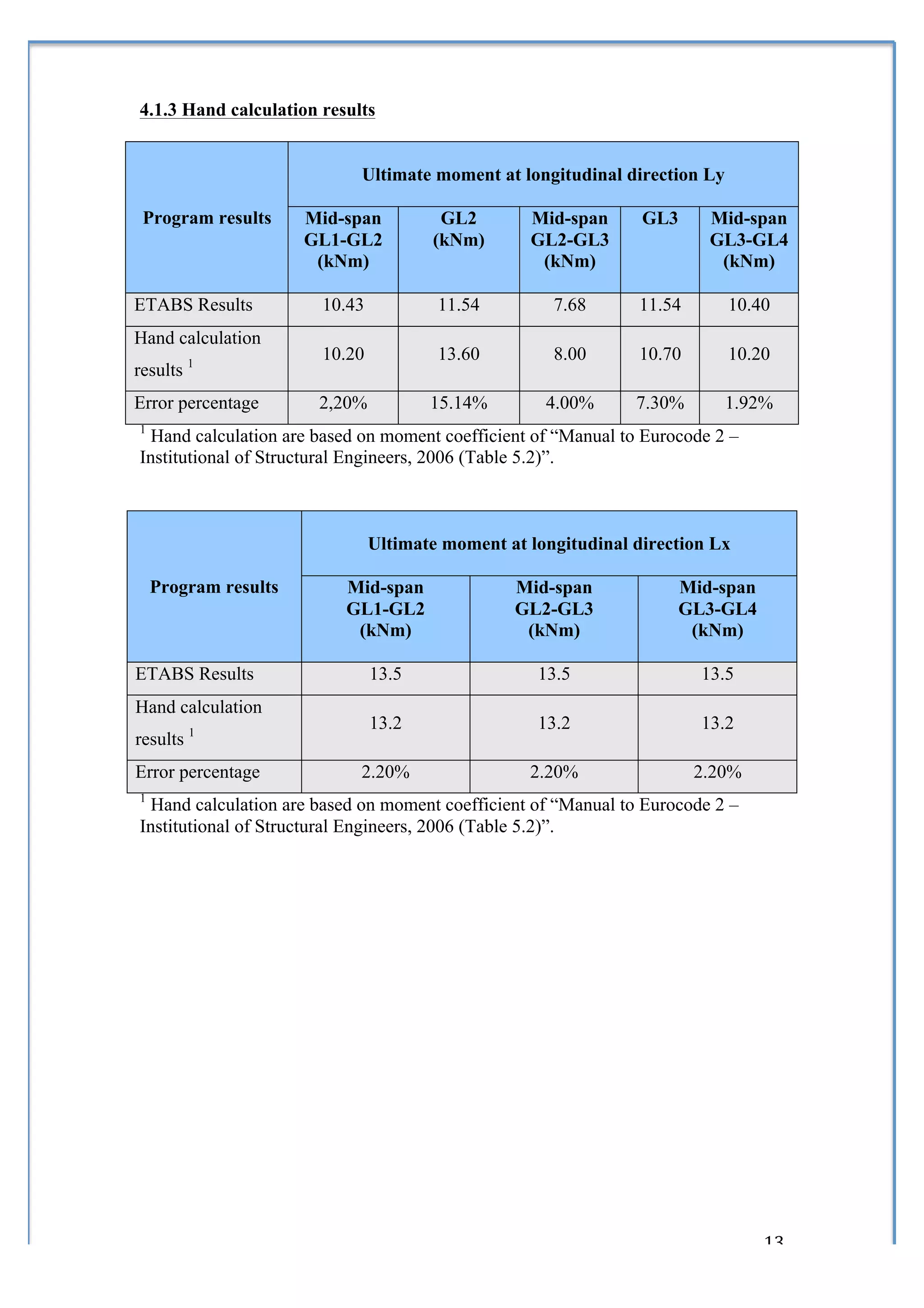
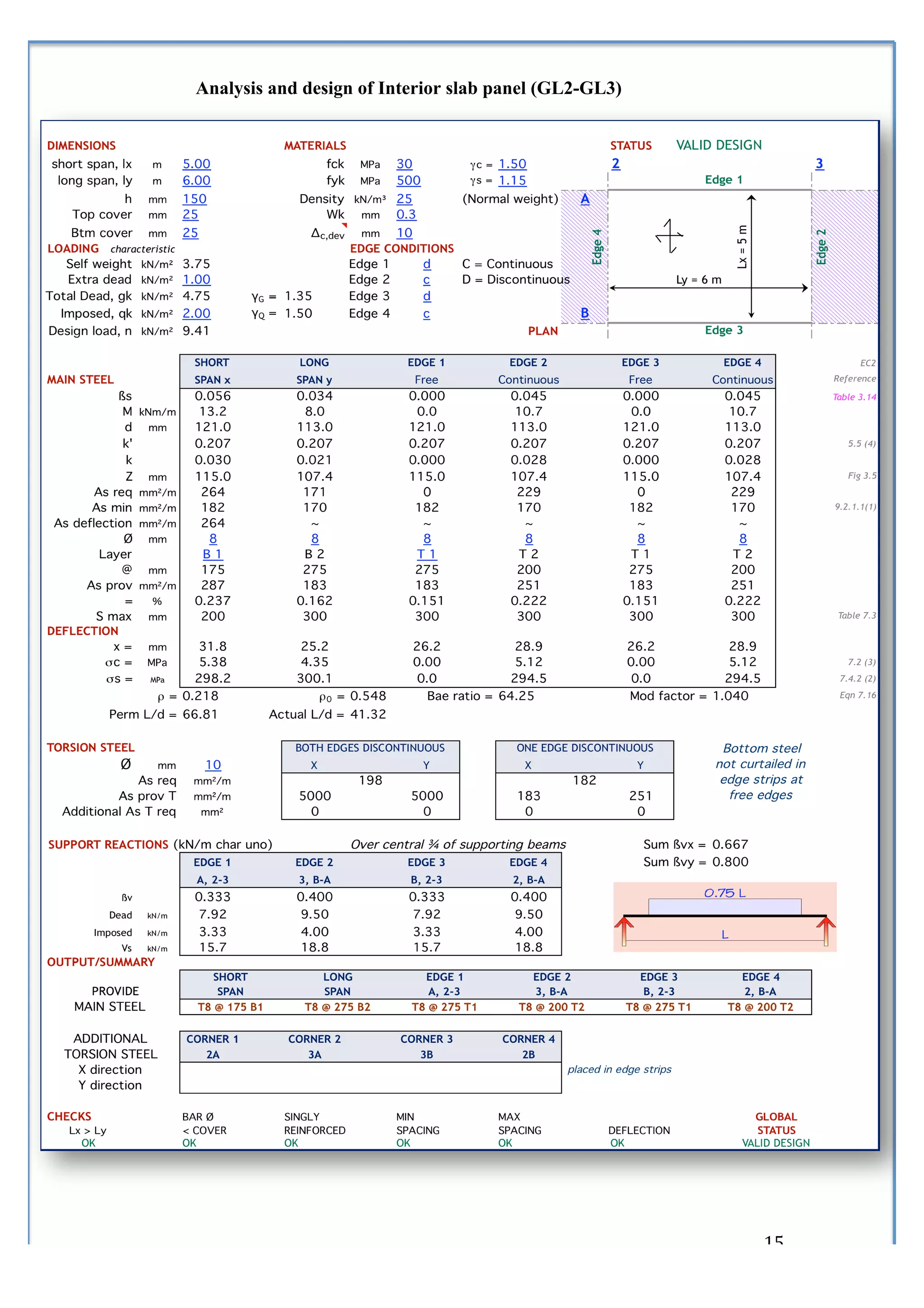
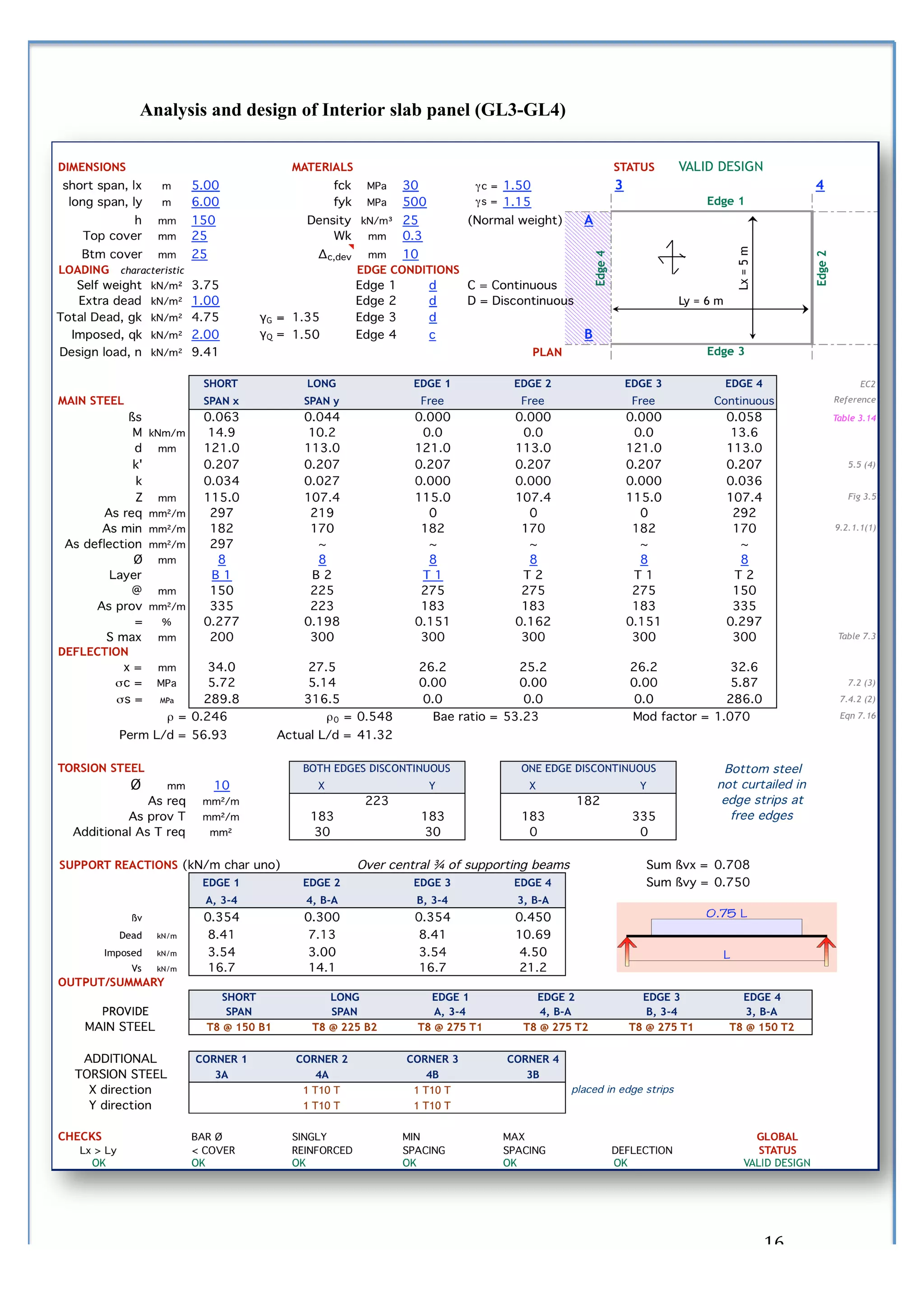
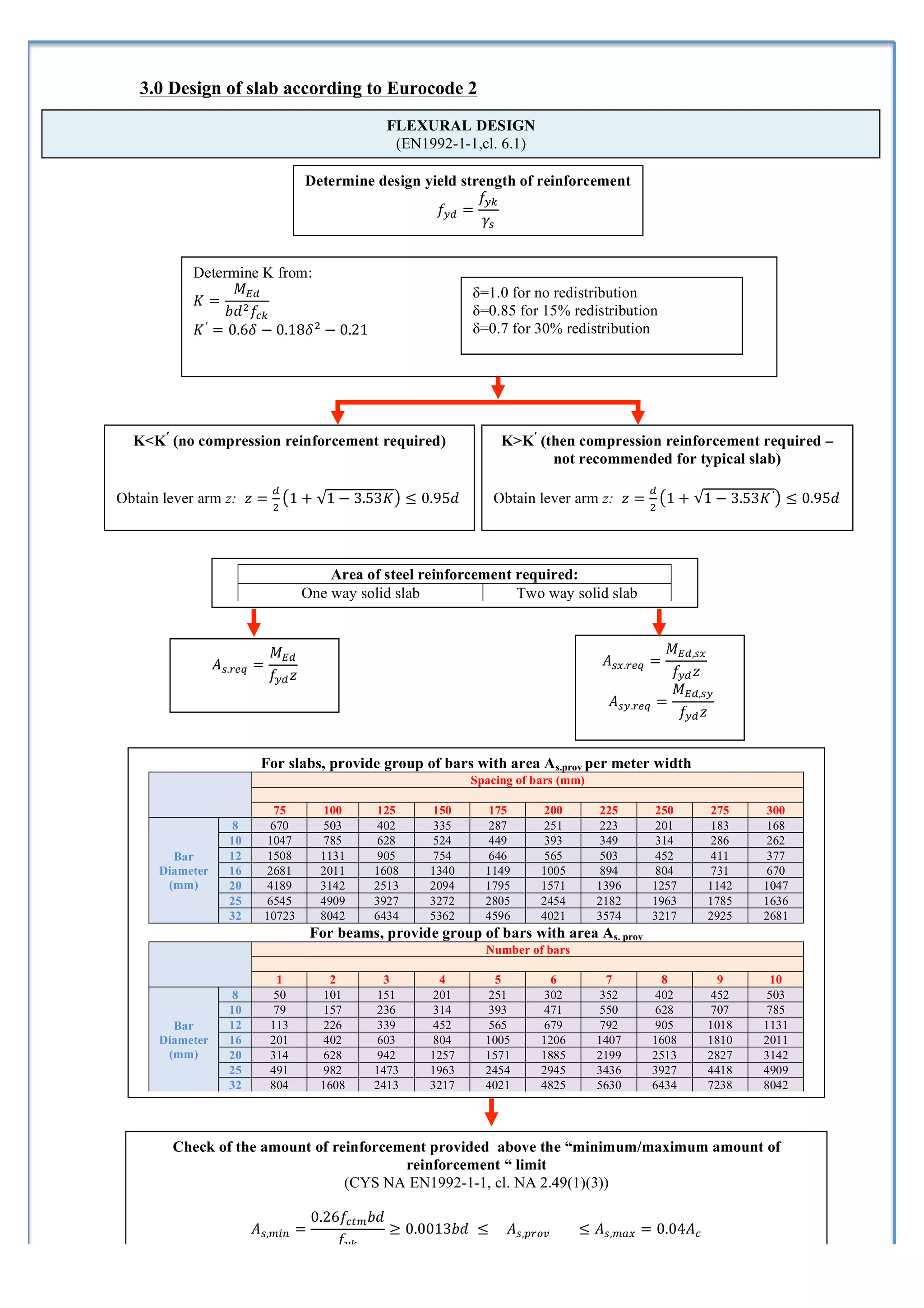
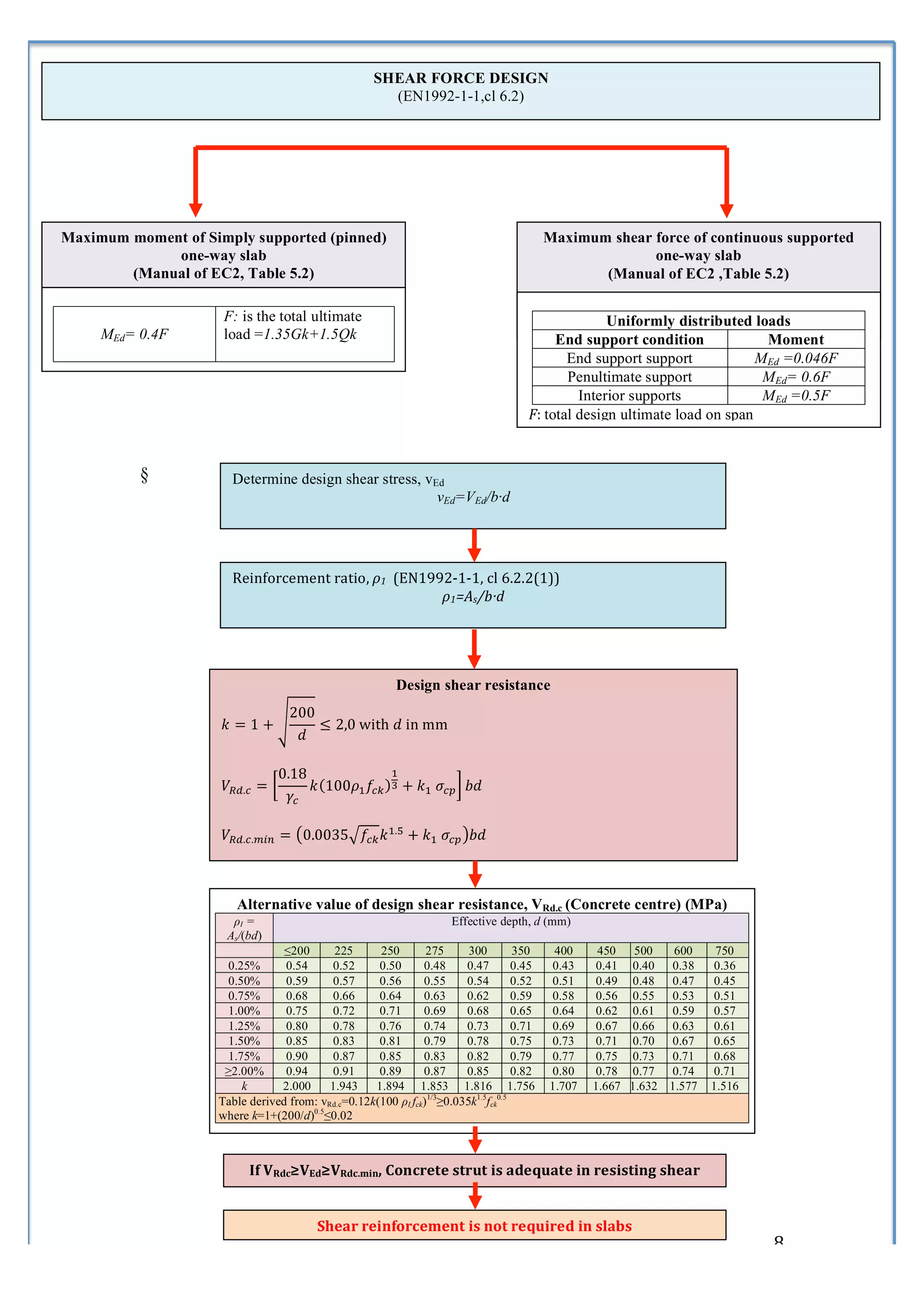
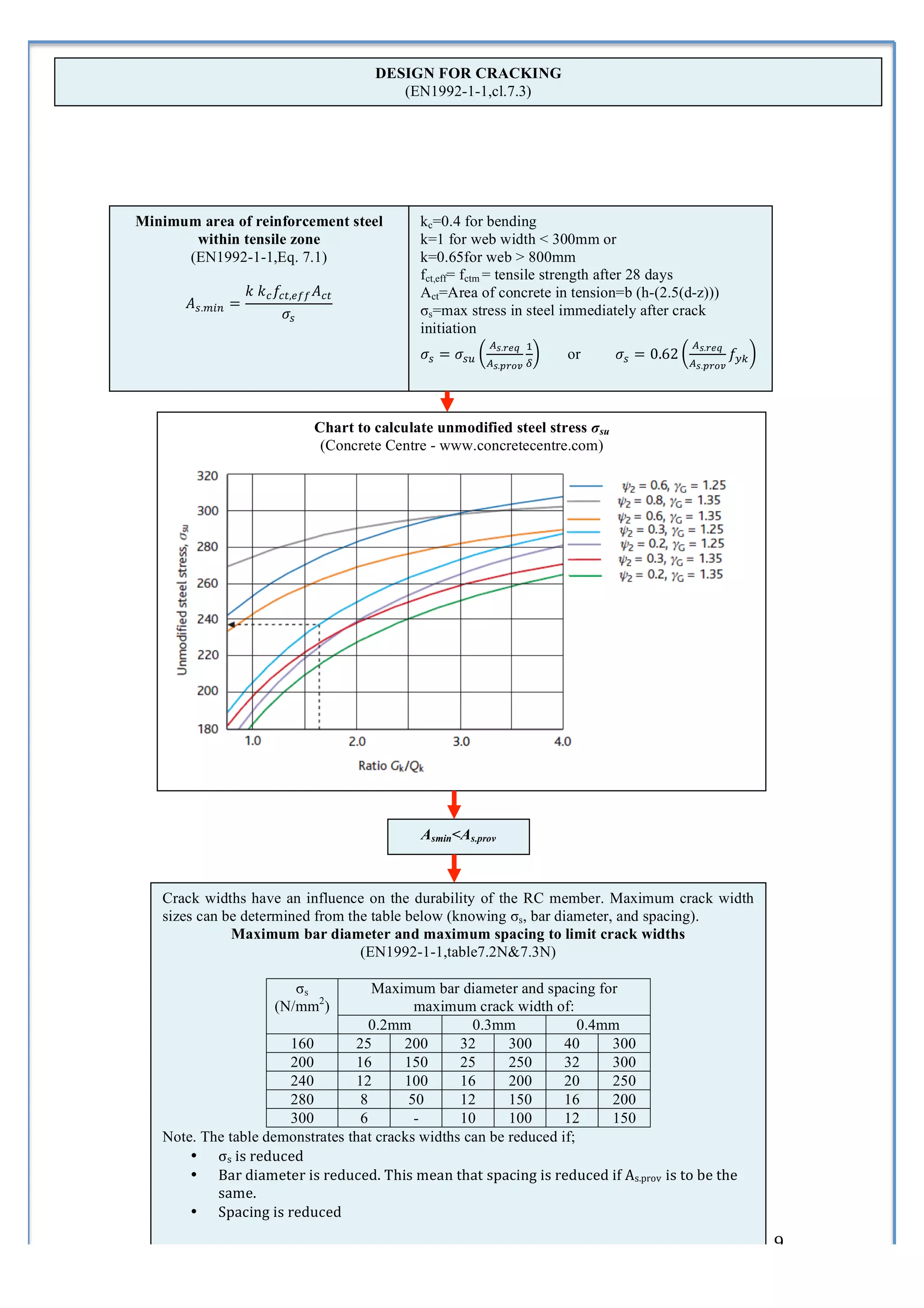
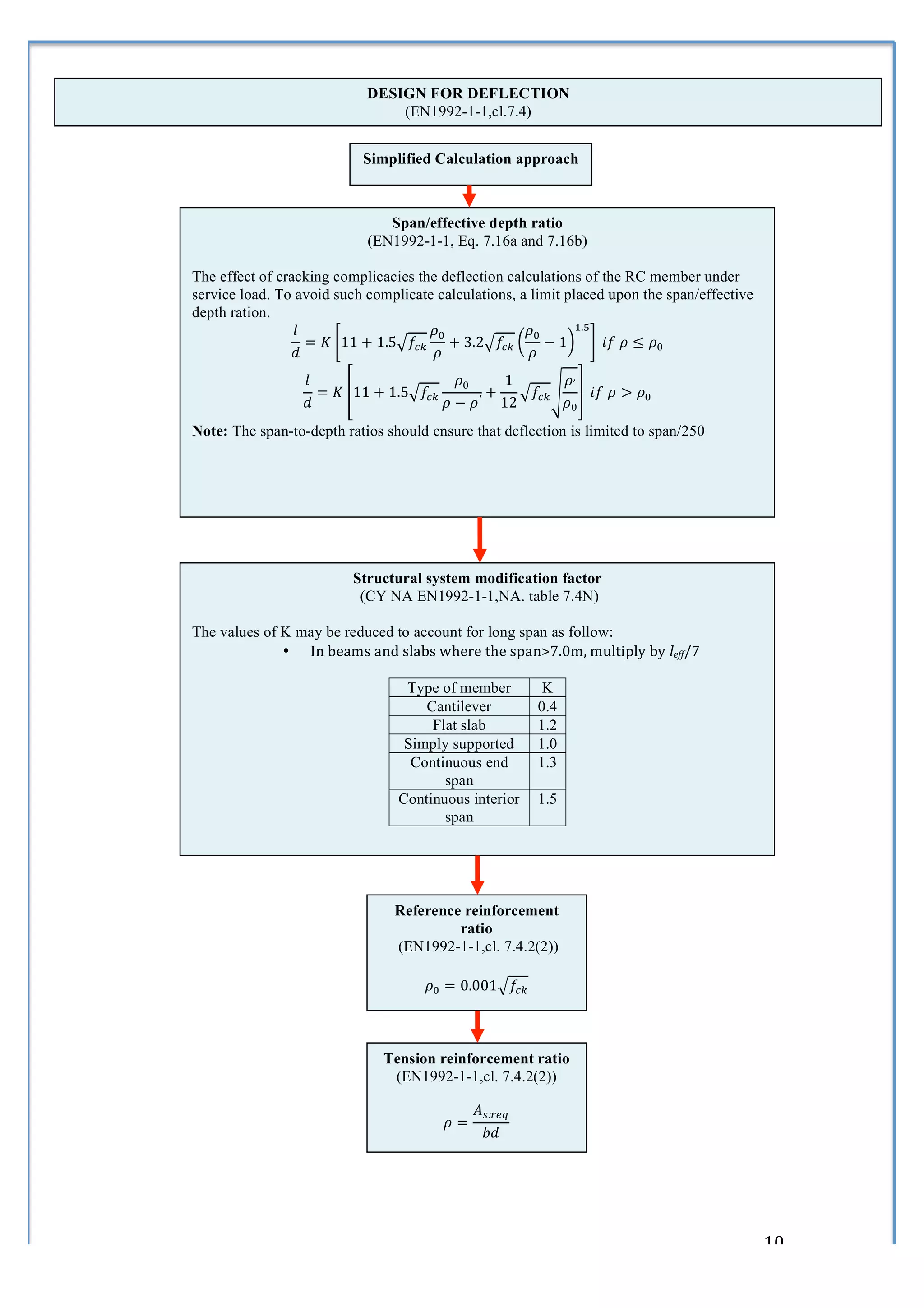
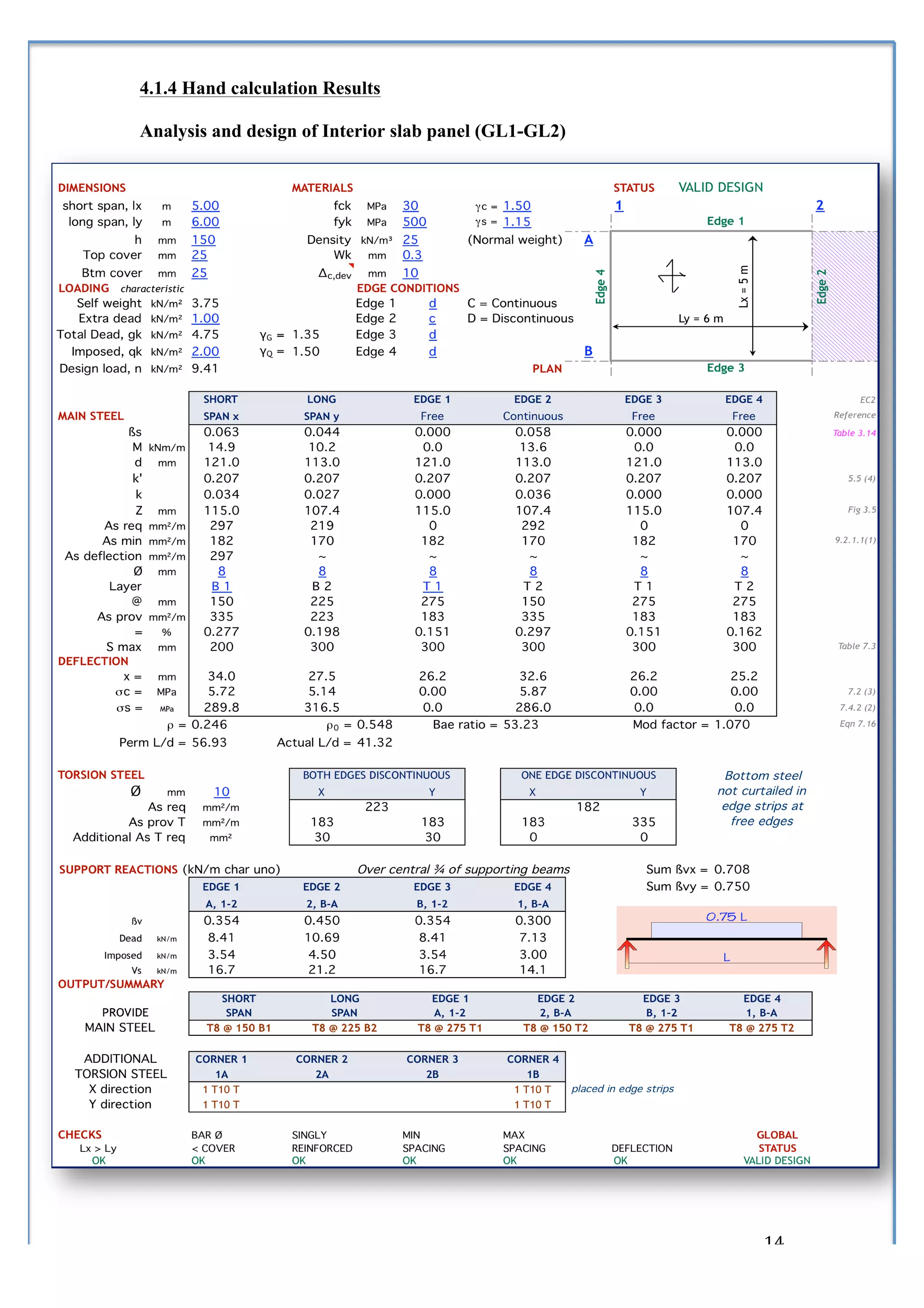
The document provides a summary of modeling and analyzing slabs in ETABS, including: 1) Common assumptions made in slab modeling such as element type, meshing, shape, and acceptable error. 2) Steps for initial analysis including sketching expected results and comparing total loads. 3) Formulas and coefficients for calculating maximum bending moments in one-way and two-way slabs. 4) A process for designing solid slabs according to Eurocode 2 involving determining reinforcement ratios and areas.

1.
ETABS MANUAL
Part-­‐II:
Model
Analysis
&
Design
of
Slabs
According
to
Eurocode
2
AUTHOR:
VALENTINOS
NEOPHYTOU
BEng
(Hons),
MSc
REVISION
1:
April,
2013

2.
ABOUT
THIS
DOCUMENT
This
document
presents
an
example
of
analysis
design
of
slab
using
ETABS.
This
example
examines
a
simple
single
story
building,
which
is
regular
in
plan
and
elevation.
It
is
examining
and
compares
the
calculated
ultimate
moment
from
ETABS
with
hand
calculation.
Moment
coefficients
were
used
to
calculate
the
ultimate
moment.
However
it
is
good
practice
that
such
hand
analysis
methods
are
used
to
verify
the
output
of
more
sophisticated
methods.
Also,
this
document
contains
simple
procedure
(step-­‐by-­‐step)
of
how
to
design
solid
slab
according
to
Eurocode
2.
The
process
of
designing
elements
will
not
be
revolutionised
as
a
result
of
using
Eurocode
2.
Due
to
time
constraints
and
knowledge,
I
may
not
be
able
to
address
the
whole
issues.
Please
send
me
your
suggestions
for
improvement.
Anyone
interested
to
share
his/her
knowledge
or
willing
to
contribute
either
totally
a
new
section
about
ETABS
or
within
this
section
is
encouraged.
For
further
details:
My
LinkedIn
Profile:
http://www.linkedin.com/profile/view?id=125833097&trk=hb_tab_pro_top
Email:
valentinos_n@hotmail.com
Slideshare
Account: http://www.slideshare.net/ValentinosNeophytou
2

3.
Table of Contents
1.0 Slab modeling .......................................................................................................... 4
1.1 Assumptions............................................................................................................. 4
1.2 Initial step before run the analysis ........................................................................... 4
2.0 Calculation of ultimate moments ............................................................................. 5
3.0 Design of slab according to Eurocode 2 .................................................................. 7
4.0 Example 1: Analysis and design of RC slab using ETABS................................... 11
4.1 Ultimate moments results ...................................................................................... 12
4.1.1 Maximum hogging and Sagging moment at Longitudinal direction Ly............. 12
4.1.2 Maximum hogging and Sagging moment at Transverse direction Lx ................ 12
4.1.3 Hand calculation results ...................................................................................... 13
4.1.4 Hand calculation Results..................................................................................... 14
3

4.
1.0 Slab modeling
1.1 Assumptions
In preparing this document a number of assumptions have been made to avoid over
complication; the assumptions and their implications are as follows.
a) Element type : SHELL
b) Meshing (Sizing of element) : Size= min{Lmax/10 or l000mm}
c) Element shape : Ratio= Lmax/Lmin = 1 ≤ ratio ≤ 2
d) Acceptable error : 20%
1.2 Initial step before run the analysis
a) Sketch out by hand the expected results before carrying out the analysis.
b) Calculate by hand the total applied loads and compare these with the sum of
the reactions from the model results.
4

5.
2.0 Calculation of ultimate moments
Maximum moments of two-way slabs
If ly/lx < 2: Design as a Two-way slab
If lx/ly > 2: Deisgn as a One-way slab
Note:
lx is the longer span
ly is the shorter span
Maximum moment of Simply supported (pinned) two-way slab
Bending moment coefficient for simply supported slab
Msx= asxnlx2 in n: is the ultimate load m2
direction of span lx
2
ly/lx 1.0 1.1 1.2 1.3 1.4 1.5 1.75 2.0
Msy= asynlx in n: is the ultimate load m2 asx 0.062 0.074 0.084 0.093 0.099 0.104 0.113 0.118
direction of span ly asy 0.062 0.061 0.059 0.055 0.051 0.046 0.037 0.029
Maximum moment of Restrained supported (fixed) two-way slab
Msx= asxnlx2 in n: is the ultimate load m2
direction of span lx
Msy= asynlx2 in n: is the ultimate load m2
direction of span ly
Bending moment coefficient for two way rectangular slab supported by beams
(Manual of EC2 ,Table 5.3)
Type of
panel and moment Short span coefficient for value of Ly/Lx Long-span coefficients for all
considered 1.0 1.25 1.5 1.75 2.0 values of Ly/Lx
Interior panels
Negative moment at continuous edge 0.031 0.044 0.053 0.059 0.063 0.032
Positive moment at midspan 0.024 0.034 0.040 0.044 0.048 0.024
One short edge discontinuous
Negative moment at continuous edge 0.039 0.050 0.058 0.063 0.067 0.037
Positive moment at midspan
0.029 0.038 0.043 0.047 0.050 0.028
One long edge discontinuous
Negative moment at continuous edge 0.039 0.059 0.073 0.083 0.089 0.037
Positive moment at midspan 0.030 0.045 0.055 0.062 0.067 0.028
Two adjacent edges discontinuous
Negative moment at continuous edge 0.047 0.066 0.078 0.087 0.093 0.045
Positive moment at midspan 0.036 0.049 0.059 0.065 0.070 0.034
5

6.
Maximum moments of one-way slabs
If ly/lx < 2: Design as a Two-way slab
If lx/ly > 2: Deisgn as a One-way slab
Note: lx is the longer span
ly is the shorter span
Maximum moment of Simply supported (pinned) Maximum moment of continuous supported one-
one-way slab way slab
(Manual of EC2, Table 5.2) (Manual of EC2 ,Table 5.2)
L: is the effective span
F: is the total ultimate Uniformly distributed loads
MEd= 0.086FL load =1.35Gk+1.5Qk End support condition Moment
L: is the effective span End support support MEd =-0.040FL
Note: Allowance has been made in the coefficients in End span MEd =0.075FL
Table 5.2 for 20% redistribution of moments. Penultimate support MEd= -0.086FL
Interior spans MEd =0.063FL
Interior supports MEd =-0.063FL
F:
total design ultimate load on span
L: is the effective span
Note: Allowance has been made in the coefficients in
Table 5.2 for 20% redistribution of moments.
6

7.
3.0 Design of slab according to Eurocode 2
FLEXURAL DESIGN
(EN1992-1-1,cl. 6.1)
Determine design yield strength of reinforcement
𝑓!"
𝑓!" =
𝛾!
Determine K from:
𝑀!" δ=1.0 for no redistribution
𝐾= !
𝑏𝑑 𝑓!" δ=0.85 for 15% redistribution
𝐾 ′ = 0.6𝛿 − 0.18𝛿 ! − 0.21 δ=0.7 for 30% redistribution
K<K′ (no compression reinforcement required) K>K′ (then compression reinforcement required –
not recommended for typical slab)
! !
Obtain lever arm z: 𝑧 = !1 + √1 − 3.53𝐾! ≤ 0.95𝑑 Obtain lever arm z: 𝑧 = !1 + √1 − 3.53𝐾 ′ ! ≤ 0.95𝑑
! !
Area of steel reinforcement required:
One way solid slab Two way solid slab
𝑀!" 𝑀!",!"
𝐴!.!"# =
𝐴!".!"# =
𝑓!" 𝑧 𝑓!" 𝑧
𝑀!",!"
𝐴!".!"# =
𝑓!" 𝑧
For slabs, provide group of bars with area A s.prov per meter width
Spacing of bars (mm)
75 100 125 150 175 200 225 250 275 300
8 670 503 402 335 287 251 223 201 183 168
10 1047 785 628 524 449 393 349 314 286 262
Bar 12 1508 1131 905 754 646 565 503 452 411 377
Diameter 16 2681 2011 1608 1340 1149 1005 894 804 731 670
(mm) 20 4189 3142 2513 2094 1795 1571 1396 1257 1142 1047
25 6545 4909 3927 3272 2805 2454 2182 1963 1785 1636
32 10723 8042 6434 5362 4596 4021 3574 3217 2925 2681
For beams, provide group of bars with area As. prov
Number of bars
1 2 3 4 5 6 7 8 9 10
8 50 101 151 201 251 302 352 402 452 503
10 79 157 236 314 393 471 550 628 707 785
Bar 12 113 226 339 452 565 679 792 905 1018 1131
Diameter 16 201 402 603 804 1005 1206 1407 1608 1810 2011
(mm) 20 314 628 942 1257 1571 1885 2199 2513 2827 3142
25 491 982 1473 1963 2454 2945 3436 3927 4418 4909
32 804 1608 2413 3217 4021 4825 5630 6434 7238 8042
Check of the amount of reinforcement provided above the “minimum/maximum amount of
reinforcement “ limit
(CYS NA EN1992-1-1, cl. NA 2.49(1)(3))
0.26𝑓!"# 𝑏𝑑
𝐴!,!"# = ≥ 0.0013𝑏𝑑 ≤ 𝐴!,!"#$ ≤ 𝐴!,!"# = 0.04𝐴!
𝑓!" 7

8.
SHEAR FORCE DESIGN
(EN1992-1-1,cl 6.2)
Maximum moment of Simply supported (pinned) Maximum shear force of continuous supported
one-way slab one-way slab
(Manual of EC2, Table 5.2) (Manual of EC2 ,Table 5.2)
F: is the total ultimate Uniformly distributed loads
MEd= 0.4F load =1.35Gk+1.5Qk End support condition Moment
End support support MEd =0.046F
Penultimate support MEd= 0.6F
Interior supports MEd =0.5F
F:
total design ultimate load on span
§ Determine design shear stress, vEd
vEd=VEd/b·d
Reinforcement
ratio,
ρ1
(EN1992-­‐1-­‐1,
cl
6.2.2(1))
ρ1=As/b·d
Design shear resistance
200
𝑘 =1+! ≤ 2,0 with 𝑑 in mm
𝑑
0.18 !
𝑉!".! = ! 𝑘(100𝜌! 𝑓!" )! + 𝑘! 𝜎!" ! 𝑏𝑑
𝛾!
𝑉!".!.!"# = !0.0035!𝑓!" 𝑘 !.! + 𝑘! 𝜎!" !𝑏𝑑
Alternative value of design shear resistance, VRd.c (Concrete centre) (ΜΡa)
ρI = Effective depth, d (mm)
As/(bd)
≤200 225 250 275 300 350 400 450 500 600 750
0.25% 0.54 0.52 0.50 0.48 0.47 0.45 0.43 0.41 0.40 0.38 0.36
0.50% 0.59 0.57 0.56 0.55 0.54 0.52 0.51 0.49 0.48 0.47 0.45
0.75% 0.68 0.66 0.64 0.63 0.62 0.59 0.58 0.56 0.55 0.53 0.51
1.00% 0.75 0.72 0.71 0.69 0.68 0.65 0.64 0.62 0.61 0.59 0.57
1.25% 0.80 0.78 0.76 0.74 0.73 0.71 0.69 0.67 0.66 0.63 0.61
1.50% 0.85 0.83 0.81 0.79 0.78 0.75 0.73 0.71 0.70 0.67 0.65
1.75% 0.90 0.87 0.85 0.83 0.82 0.79 0.77 0.75 0.73 0.71 0.68
≥2.00% 0.94 0.91 0.89 0.87 0.85 0.82 0.80 0.78 0.77 0.74 0.71
k 2.000 1.943 1.894 1.853 1.816 1.756 1.707 1.667 1.632 1.577 1.516
1/3 1.5 0.5
Table derived from: vRd.c=0.12k(100 ρI fck) ≥0.035k fck
where k=1+(200/d)0.5≤0.02
If
VRdc≥VEd≥VRdc.min,
Concrete
strut
is
adequate
in
resisting
shear
stress
Shear
reinforcement
is
not
required
in
slabs
8

9. DESIGN FOR CRACKING
(EN1992-1-1,cl.7.3)
Minimum area of reinforcement steel kc=0.4 for bending
within tensile zone k=1 for web width < 300mm or
(EN1992-1-1,Eq. 7.1) k=0.65for web > 800mm
fct,eff= fctm = tensile strength after 28 days
𝑘 𝑘! 𝑓!",!"" 𝐴!" Act=Area of concrete in tension=b (h-(2.5(d-z)))
𝐴!.!!" = σs=max stress in steel immediately after crack
𝜎!
initiation
!!.!"# ! !!.!"#
𝜎! = 𝜎!" ! ! or 𝜎! = 0.62 ! 𝑓 !
!!.!"#$ ! !!.!"#$ !"
Chart to calculate unmodified steel stress σsu
(Concrete Centre - www.concretecentre.com)
Asmin<As.prov
Crack widths have an influence on the durability of the RC member. Maximum crack width
sizes can be determined from the table below (knowing σs, bar diameter, and spacing).
Maximum bar diameter and maximum spacing to limit crack widths
(EN1992-1-1,table7.2N&7.3N)
σs Maximum bar diameter and spacing for
(N/mm2) maximum crack width of:
0.2mm 0.3mm 0.4mm
160 25 200 32 300 40 300
200 16 150 25 250 32 300
240 12 100 16 200 20 250
280 8 50 12 150 16 200
300 6 - 10 100 12 150
Note. The table demonstrates that cracks widths can be reduced if;
• σs
is
reduced
• Bar
diameter
is
reduced.
This
mean
that
spacing
is
reduced
if
As.prov
is
to
be
the
same.
• Spacing
is
reduced
9

10.
DESIGN FOR DEFLECTION
(EN1992-1-1,cl.7.4)
Simplified Calculation approach
Span/effective depth ratio
(EN1992-1-1, Eq. 7.16a and 7.16b)
The effect of cracking complicacies the deflection calculations of the RC member under
service load. To avoid such complicate calculations, a limit placed upon the span/effective
depth ration.
𝑙 𝜌! 𝜌! !.!
= 𝐾 !11 + 1.5!𝑓!" + 3.2!𝑓!" ! − 1! ! 𝑖𝑓 𝜌 ≤ 𝜌!
𝑑 𝜌 𝜌
𝑙 𝜌! 1 𝜌,
= 𝐾 !11 + 1.5!𝑓!" + !𝑓!" ! ! 𝑖𝑓 𝜌 > 𝜌!
𝑑 𝜌 − 𝜌 12
′ 𝜌!
Note: The span-to-depth ratios should ensure that deflection is limited to span/250
Structural system modification factor
(CY NA EN1992-1-1,NA. table 7.4N)
The values of K may be reduced to account for long span as follow:
• In
beams
and
slabs
w here
the
span>7.0m,
multiply
by
leff/7
Type of member K
Cantilever 0.4
Flat slab 1.2
Simply supported 1.0
Continuous end 1.3
span
Continuous interior 1.5
span
Reference reinforcement
ratio
(EN1992-1-1,cl. 7.4.2(2))
𝜌! = 0.001!𝑓!"
Tension reinforcement ratio
(EN1992-1-1,cl. 7.4.2(2))
𝐴!.!"#
𝜌=
𝑏𝑑
10

11.
4.0 Example 1: Analysis and design of RC slab using ETABS
1. Dimensions:
Depth of slab, h: h=150mm
Length in longitudinal direction, Ly: Ly=6m
Length in transverse direction, Lx: Lx=5m
Number of slab panels: N=3
2. Loads:
Dead load:
Self weight, gk.s: gk.s=3.75kN/m2
Extra dead load, gk.e: gk.e=1.00kN/m2
Total dead load, Gk: Gk=4.75kN/m2
Live load:
Live load, qk: gk=2.00kN/m2
Total live load, Qk: Qk=2.00kN/m2
3. Load combination:
Total load on slab: 1.35Gk+1.5Qk=
COMB1: 1.35*4.75+1.5*2.00=9.1kN/m2
4. Layout of model:
11

12.
4.1 Ultimate moments results
4.1.1 Maximum hogging and Sagging moment at Longitudinal direction Ly
4.1.2 Maximum hogging and Sagging moment at Transverse direction Lx
12

13.
4.1.3 Hand calculation results
Ultimate moment at longitudinal direction Ly
Program results Mid-span GL2 Mid-span GL3 Mid-span
GL1-GL2 (kNm) GL2-GL3 GL3-GL4
(kNm) (kNm) (kNm)
ETABS Results 10.43 11.54 7.68 11.54 10.40
Hand calculation
10.20 13.60 8.00 10.70 10.20
results 1
Error percentage 2,20% 15.14% 4.00% 7.30% 1.92%
1
Hand calculation are based on moment coefficient of “Manual to Eurocode 2 –
Institutional of Structural Engineers, 2006 (Table 5.2)”.
Ultimate moment at longitudinal direction Lx
Program results Mid-span Mid-span Mid-span
GL1-GL2 GL2-GL3 GL3-GL4
(kNm) (kNm) (kNm)
ETABS Results 13.5 13.5 13.5
Hand calculation
13.2 13.2 13.2
results 1
Error percentage 2.20% 2.20% 2.20%
1
Hand calculation are based on moment coefficient of “Manual to Eurocode 2 –
Institutional of Structural Engineers, 2006 (Table 5.2)”.
13

14.
4.1.4 Hand calculation Results
Analysis and design of Interior slab panel (GL1-GL2)
14

15.
Analysis and design of Interior slab panel (GL2-GL3)
15

16.
Analysis and design of Interior slab panel (GL3-GL4)
16