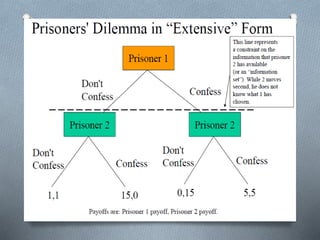
This document provides an overview of game theory, including its founders John von Neumann and John Nash. Game theory is the study of strategic decision making among rational players where outcomes depend on the choices of all. It has applications in economics, politics, and biology. Key concepts discussed include Nash equilibrium, where no player benefits from changing strategies alone; the prisoner's dilemma game; and the tit-for-tat strategy of reciprocal cooperation and defection. The document outlines the assumptions, elements, and applications of game theory.