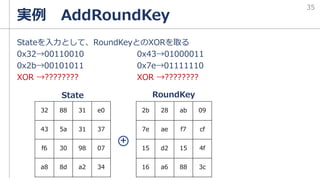
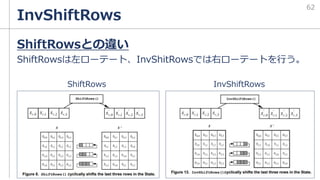
The document provides an overview of the Advanced Encryption Standard (AES) encryption algorithm in Japanese. It discusses AES being selected as the encryption standard by NIST in 1997. It then explains the basic processing steps of AES including AddRoundKey, SubBytes, ShiftRows, and MixColumns. It notes AES uses a block size of 128 bits and has key sizes of 128, 192, and 256 bits, corresponding to 10, 12, and 14 rounds respectively. It also discusses AES being used for Wi-Fi encryption through the WPA2 protocol.

























![KeyExpansion
47
KeyExpansion(byte key[4*Nk], word w[Nb*(Nr+1)], Nk)
begin
word temp
i = 0
while (i < Nk)
w[i] = word(key[4*i], key[4*i+1], key[4*i+2], key[4*i+3])
i = i + 1
end while
i = Nk
while (i < Nb * (Nr+1))
temp = w[i-1]
if (i mod Nk = 0)
temp = SubWord(RotWord(temp)) xor Rcon[i/Nk]
else if (Nk > 6 and i mod Nk = 4)
temp = SubWord(temp)
end if
w[i] = w[i-Nk] xor temp
i = i + 1
end while
end
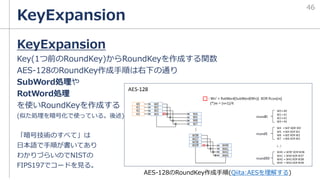
FIPS197に書いてある
疑似コード
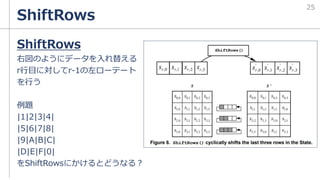
C言語とアセンブラが
混ざったような形を
しているが、今回は
大まかな流れを掴み
たいだけなので特に
別言語に変換はしない](https://image.slidesharecdn.com/aes-210625133500/85/AES-47-320.jpg)
![実例 KeyExpansion
48
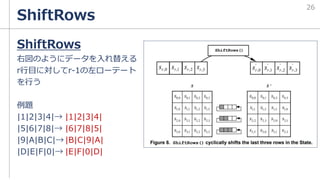
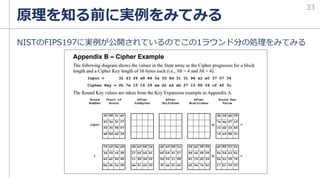
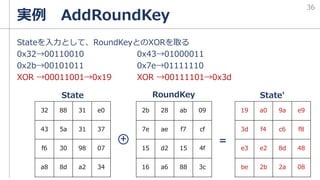
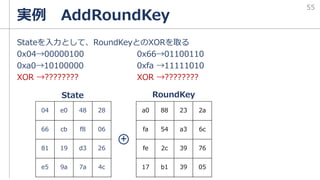
逐次コードを参照しながらFIPS197に書いてあるAES-128のサブ鍵作成例を
読んで理解していく。w[i]={4byte}={32bit}
AES-128はその名の通り鍵長が128bitである
→つまり、ラウンドごとの鍵はw[i]4つ分
w[0]={2b7e1516}
w[1]={28aed2a6}
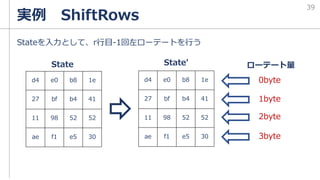
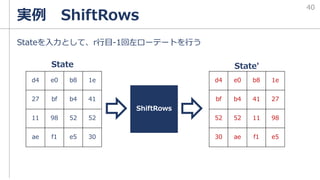
w[2]={abf71588}
w[3]={09cf4f3c}
---ここまでで1セット---
w[4]={???}←ここから計算による鍵の作成を行っていく
i = 0
while (i < Nk)
w[i] = word(key[4*i], key[4*i+1], key[4*i+2], key[4*i+3])
i = i + 1
end while
w[0]~w[3]までの疑似プログラム
最初のRoundKeyはCipher Keyとして自分で任意に決めた鍵の値 (初期値)w[0]~w[3]](https://image.slidesharecdn.com/aes-210625133500/85/AES-48-320.jpg)
![実例 KeyExpansion
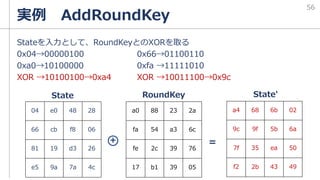
まずw[4]を作ることを考える
tempにはひとつ前の鍵要素を
入れる
w[3]は{09cf4f3c}
RotWord
1byte分左ローテートをする
09cf4f3cは、
|09|cf|4f|3c|
と考えると
AES-128のRoundKey作成例
49
while (i < Nb * (Nr+1))
temp = w[i-1]
if (i mod Nk = 0)
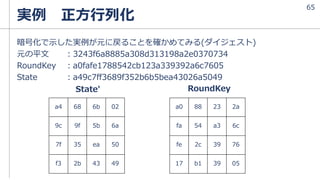
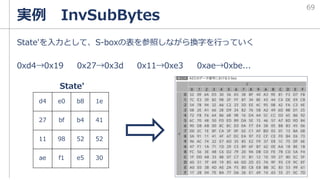
temp = SubWord(RotWord(temp)) xor Rcon[i/Nk]](https://image.slidesharecdn.com/aes-210625133500/85/AES-49-320.jpg)
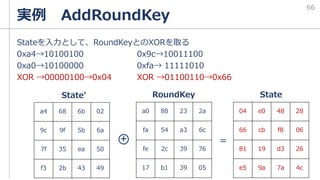
![実例 KeyExpansion
RotWord
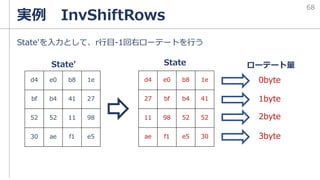
1byte分左ローテートをする
09cf4f3cは、
|09|cf|4f|3c|
と考えると、
|cf|4f|3c|09|
となる。
AES-128のRoundKey作成例
50
while (i < Nb * (Nr+1))
temp = w[i-1]
if (i mod Nk = 0)
temp = SubWord(RotWord(temp)) xor Rcon[i/Nk]](https://image.slidesharecdn.com/aes-210625133500/85/AES-50-320.jpg)
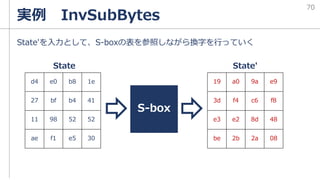
![実例 KeyExpansion
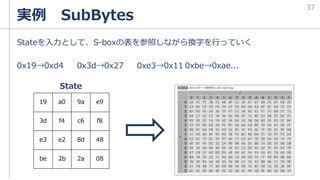
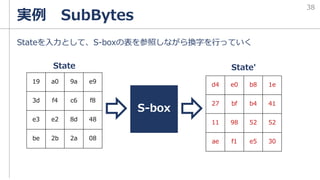
SubWord
SubWordはS-boxの表に
基づいた換字を行う
「暗号技術のすべて」p.174
を参照しながらSubBytesと
同じように処理をすると、
|cf|4f|3c|09|
から
|8a|84|eb|01|
AES-128のRoundKey作成例
51
while (i < Nb * (Nr+1))
temp = w[i-1]
if (i mod Nk = 0)
temp = SubWord(RotWord(temp)) xor Rcon[i/Nk]](https://image.slidesharecdn.com/aes-210625133500/85/AES-51-320.jpg)
![実例 KeyExpansion
RotWord,SubWord処理をしたら
RconとXORする、とある
Rcon
RconはRoundConstantの略で、
ラウンドコンスタント定数と訳す
定数と書いてあるが、コードを
見るとわかるように計算している
Rcon[変数iをKey数Nkで割った値]
これを使ってtempとXORを行う AES-128のRoundKey作成例
52
while (i < Nb * (Nr+1))
temp = w[i-1]
if (i mod Nk = 0)
temp = SubWord(RotWord(temp)) xor Rcon[i/Nk]](https://image.slidesharecdn.com/aes-210625133500/85/AES-52-320.jpg)
![実例 KeyExpansion
Rcon
XORをやっていく
temp={8a84eb01}
Rcon={01000000}
0はXORしても変わらないから、
aと1だけを考える
0xa=1010
0x1=0001
xor=1011=b
よって、temp={8b84eb01} AES-128のRoundKey作成例
53
while (i < Nb * (Nr+1))
temp = w[i-1]
if (i mod Nk = 0)
temp = SubWord(RotWord(temp)) xor Rcon[i/Nk]](https://image.slidesharecdn.com/aes-210625133500/85/AES-53-320.jpg)
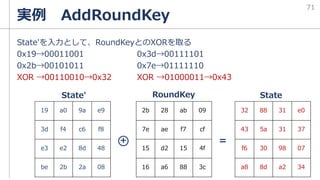
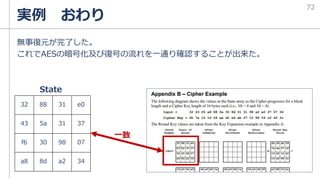
![実例 KeyExpansion
長々とやってきたKeyExpantionの最後の処理
を考える
今回はw[4]を作ることを考えている。また鍵数Nk=4より、
w[0] ={2b7e1516}
={00101011011111100001010100010110}
temp ={8b84eb01}
={10001011100001001110101100000001}
XOR ={10100000111110101111111000010111}
={a0fafe17}
作成例のサブ鍵例と一致→
これを繰り返すことで各ラウンドのカギを作っている
(なおi%4=!0(左から2列目以降)のときはRotWord/SubWord/Rconは実行しない)
54
w[i] = w[i-Nk] xor temp](https://image.slidesharecdn.com/aes-210625133500/85/AES-54-320.jpg)













![【質問】
・10ページ
暗号化アルゴリズムの方法といってはいけない理由?
【先生のコメント】(補足説明)
・アフィン変換
幾何学
線形→直線
直線ってことは方程式が出る
係数は変換そのもの
行列だけで積を変えるのは線形変換ということ
原点(0)は動かしちゃだめだけど向きを変えるとき、これも線形変換である
---ここまでは線形変換---
平行移動だけならベクトルの概念でいける
でもこれをやると原点(0)から動かしているということで、線形ではなくな
る
スライドのアフィン変換の右側に出てくる一列→ベクトル【平行移動】
---これはアフィン変換---
アフィン変換=線形変換+平行移動(非線形)
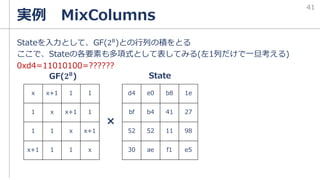
・GF
GF(2^8)[x]/既約多項式
既約多項式はx^8を含む式であること
の結果は必ずx^7以下になる。
マックス8項になる。→桁あふれが発生しない
→係数が0または1となる
1ビット分のデータだからGF(2)になる
既約多項式の割り算が発生するが、割り算は時間が掛かるので出来るだけし
たくない
既約多項式で割り切れたら0なので(剰余の世界だから)、
既約多項式=0 より、
x^8
=x^4+x^3+x+1
=0x1BでXOR
発表後のコメント
79](https://image.slidesharecdn.com/aes-210625133500/85/AES-79-320.jpg)