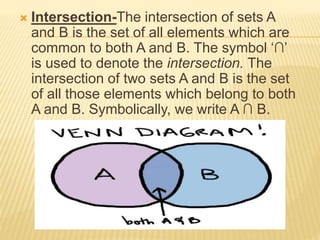
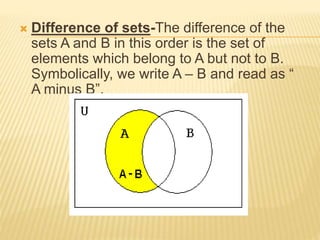
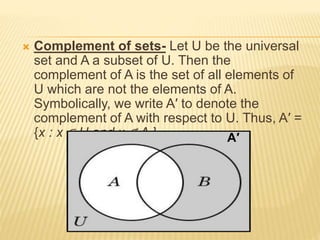
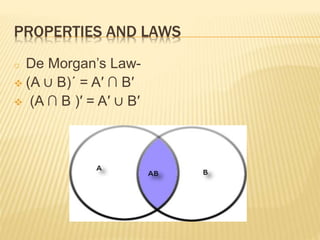
A set is a collection of distinct objects. There are two ways to describe a set: roster form lists the elements between braces, and set-builder form uses a characteristic property P(x). Sets can be infinite, finite, empty, or singleton. Two sets are equal if they contain the same elements, and equivalent if they have the same number of elements. A set is a subset if all its elements are contained in another set, called the superset. Closed and open intervals are examples of subsets of real numbers. The power set is the collection of all subsets, and the universal set contains all sets in a given context. Venn diagrams use circles and rectangles to represent relationships between sets. Common set operations include union

2. What is a set?
Set is a well defined
collection of objects.

3. TWO FORMS OF SET
Roster Form- In this method a set is described by
listing elements, separated by commas, within
braces { }.
Set-Builder Form-In this method, a set is
described by a characterizing property P(x) of
its element x. In such a case the set is described
by {x:P(x) holds}.

4. TYPES OF SET
 Infinite set- A set containing infinitely many
numbers of elements is called an infinite set.
Eg- B{1,2,3,4,5…………}
 Finite set- A set having finite number of
elements is called a finite set.
Eg- A{1,2,4,8,16,32}

5.  Empty set- A set having no element is
called an empty set. It is represented by
symbol φ
Eg- A={ }
B=φ
C={x:x R, 3<x<1}
 Singleton set- The set having only single
element is called singleton set.
Eg- A{1}
B{3}

6.  Equal set- Two sets A and B are set to be
equal if every elements of A is a member
of B, and every of B is a member of A and
vice-versa.
Eg- A={1,2,5,6}
B={5,6,2,1}
A=B
 Equivalent sets- Two finite sets A and B
are equivalent if their cardinal number are
same i.e.-n(A)=n(B)

7. SUBSET AND SUPERSET
 Subset- Let A and B be two sets. If every
element of A is an element of B, then A is
called a subset of B. Subset is denoted by ⊂.
A ⊂ B if a ∈ A ⇒ a ∈ B
 Superset- If every element of A belongs to B
then B will be the superset of A.

8. INTERVAL AS SUBSET
 Closed interval- Let a and b be two given
real number such that a<b. Then the set of
all real numbers x such that a ≤ x ≤ b is
called a closed interval and denoted by [a,b].
 Open interval-If a and b are two real
numbers such that a<b ,then the of all real
numbers x satisfying a<x<b is called an open
interval and is denoted by (a,b).

9. UNIVERSAL AND POWER SET
 Power set-The collection of all subsets of a
set A is called the power set of A. It is
denoted by P(A).
 Universal set-A set that contains all sets in
a given context is called the universal set.

10. VENN DIAGRAM
Most of the relationships between sets can be
represented by means of diagrams which are known
as Venn diagrams. Venn diagrams are named after
the English logician, John Venn (1834-1883). These
diagrams consist of rectangles and closed curves
usually circles. The universal set is represented
usually by a rectangle and its subsets by circles.

11. OPERATION ON SETS
 Union-Let A and B be any two sets. The union of A
and B is the set which consists of all the elements
of A and all the elements of B, the common
elements being taken only once. The symbol ‘∪’ is
used to denote the union. Symbolically, we write A
∪ B.

12.  Intersection-The intersection of sets A
and B is the set of all elements which are
common to both A and B. The symbol ‘∩’
is used to denote the intersection. The
intersection of two sets A and B is the set
of all those elements which belong to both
A and B. Symbolically, we write A ∩ B.

13.  Disjoint set-Two sets A and B are said to
be disjoint ,if A ∩ B= φ.

14.  Difference of sets-The difference of the
sets A and B in this order is the set of
elements which belong to A but not to B.
Symbolically, we write A – B and read as “
A minus B”.

15.  Complement of sets- Let U be the universal
set and A a subset of U. Then the
complement of A is the set of all elements of
U which are not the elements of A.
Symbolically, we write A′ to denote the
complement of A with respect to U. Thus, A′ =
{x : x ∈ U and x ∉ A } A′

16. PROPERTIES AND LAWS
o De Morgan’s Law-
 (A ∪ B)´ = A′ ∩ B′
 (A ∩ B )′ = A′ ∪ B′