IB Chemistry on Line Emission Spectrum, Bohr Model and Electromagnetic Spectrum
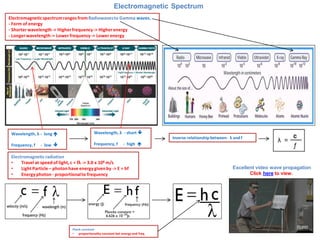
- 1. Electromagnetic Spectrum Electromagnetic spectrum ranges from Radiowaves to Gamma waves. - Form of energy - Shorter wavelength -> Higher frequency -> Higher energy - Longer wavelength -> Lower frequency -> Lower energy Electromagnetic radiation •Travel at speed of light, c = fλ -> 3.0 x 108 m/s •Light Particle – photon have energy given by -> E = hf •Energy photon - proportional to frequency Inverse relationship between- λ and f Wavelength, λ - long Frequency, f - low Wavelength, λ - short Frequency, f - high Plank constant •proportionality constant bet energy and freq Excellent video wave propagation Click here to view.
- 2. Electromagnetic Wave propagation. Wave Electromagnetic radiation Electromagnetic radiation • Moving charges/particles through space • Oscillating wave like property of electric and magnetic field • Electric and magnetic field oscillate perpendicular to each other and perpendicular to direction of wave propagation. Electromagnetic wave propagation Wave – wavelength and frequency - travel at speed of light Violet λ = 410nm Red f = c/λ = 3 x 108/410 x 10-9 = 7.31 x 1014 Hz E = hf = 6.626 x 10-34 x 7.31 x 1014 = 4.84 x 10-19 J λ = 700nm f = c/λ = 3 x 108/700 x 10-9 = 4.28 x 1014 Hz E = hf = 6.626 x 10-34 x 4.28 x 1014 = 2.83 x 10-19 J Click here to view video
- 3. Electromagnetic Wave propagation. Wave Electromagnetic radiation Simulation on Electromagnetic Propagation Click here to view simulation Click here to view simulation Click here to view simulation Electromagnetic radiation •Moving charges/particles through space •Oscillating wave like property of electric and magnetic field •Electric and magnetic field oscillate perpendicular to each other and perpendicular to direction of wave propagation. Click to view video -Wave-particle duality Is it a particle or Wave? Wave – wavelength and frequency - travel at speed of light
- 4. Electromagnetic Wave Violet λ = 410nm Red f = c/λ = 3 x 108/410 x 10-9 = 7.31 x 1014 Hz λ = 700nm f = c/λ = 3 x 108/700 x 10-9 = 4.28 x 1014 Hz Which wave have higher frequency, if both have same speed reaching Y same time? Violet Y Red X Wavelength – Distance bet two point with same phase, bet crest/troughs – unit nm Frequency – Number of cycle/repeat per unit time (cycles in 1 second) – unit Hz Click here on excellent video red /violet wave Light travel same speed Red flippers – long λ - less frequent Violet shoes – short λ - more frequent Click here to view video energy photon
- 5. http://www.astrophys-assist.com/educate/orion/orion02.htm Continuous Spectrum : Light spectrum with all wavelength/frequency Emission Line Spectrum : • Spectrum with discrete wavelength/ frequency • Emitted when excited electrons drop from higher to lower energy level Absorption Line Spectrum : • Spectrum with discrete wavelength/frequency • Absorbed when ground state electrons are excited Atomic Emission Vs Atomic Absorption Spectroscopy Ground state Excited state Electrons from excited state Emit radiation when drop to ground state Radiation emitted Emission Spectrum Electrons from ground state Absorb radiation to excited state Electrons in excited state Radiation absorbed Continuous Spectrum Vs Line Spectrum
- 6. Line Emission Spectra for Hydrogen Energy supplied to atoms • Electrons excited - ground to excited states • Electrons exist fixed energy level (quantum) • Electrons transition from higher to lower, emit energy of particular wavelength/frequency - photon • Higher the energy level, smaller the difference in energy bet successive energy level. • Spectrum converge (get closer) with increase freq. • Lines spectrum converge- energy levels also converge • Ionisation energy determined (Limit of convergence) N = 3-2, 656nm N= 4-2 486nm N= 5-2 434nm N= 6-2 410nm Visible region- Balmer Series UV region Lyman Series n=∞ → n= 1 Visible region Balmer Series n=∞ → n= 2 IR region Paschen Series n=∞ → n= 3 Line Emission Spectra • Energy supplied • Electrons surround nucleus in allowed energy states (quantum) • Excited electron return to lower energy level, photon with discrete energy/wavelength (colour) given out. • Light pass through spectroscope (prism/diffraction grating) to separate out diff colours Click here to view video Click here to view video Videos on line emission Line Emission Spectroscopy
- 7. Ground state Excited state Hydrogen Emission Spectroscopy – Visible region (Balmer Series) Line Emission Spectra for Hydrogen Visible region Balmer Series n=∞ → n= 2 Hydrogen discharge tube Hydrogen Emission Spectroscopy n = 3-2 n= 4-2 n= 5-2 λ = 656nm f = c/λ = 3 x 108/656 x 10-9 = 4.57 x 1014 Hz E = hf = 6.62 x 10-34 x 4.57 x 1014 = 3.03 x 10-19 J λ = 434nm λ = 486nm f = c/λ = 3 x 108/434 x 10-9 = 6.90 x 1014 Hz E = hf = 6.62 x 10-34 x 6.90 x 1014 = 4.56 x 10-19 J More energetic violet line Less energetic red line 2 1 3 4 5 Click here for detail notes Click here video line emission spectrum
- 8. Bohr Model for Hydrogen Atom – Ionization Energy Niels Bohr Model (1913) •Electrons orbit nucleus. •Orbits with discrete energy levels – Quantized. •Transition electron bet diff levels by absorb/emit radiation with frequency, f determined by energy diff bet levels -ΔE = hf •Energy light emit/absorb equal to diff bet energy levels Electronic Transition bet levels Energy level Bohr Model 1 2 3 4 5 ∞ Light emitted equal to difference bet energy levels, -ΔE = hf Plank equation Ionisation energy determined (Limit of convergence) Line spectrum converge (get closer) with increase freq Higher energy level n, smaller the difference in energy bet successive energy level. Lines in spectrum converge- energy levels also converge Visible region Balmer Series n=∞ → n= 2 Increase freq UV region Lyman Series n=∞ → n= 1 ΔE = hf Light energy - ΔE = hf Frequency = ΔE/h Increase freq Line spectrum converge (get closer) with increase freq Ionization energy Transition electron from 1 ->∞ line converge line converge Light given off
- 9. Energy Level/Ionization Energy Calculation 1 2 3 4 5 ∞ Formula - energy level, n (eV) Energy difference bet level 3 to 2 1 2 n = energy level Lower energy level, n -more stable electron -more – ve (-13.6eV) -Less energetic Higher energy level, n -more unstable electron -More + ve ( less negative) -More energetic Energy level, n= 1 = -13.6/n2 = -13.6/1 = -13.6 eV Energy level, n= 2 = -13.6/n2 = -13.6/22 = -3.4 eV Energy level, n= 3 = -13.6/n2 = -13.6/32 = -1.51 eV 3 4 5 Energy difference, n= 3-2 = -1.51 – (-3.4) eV = 1.89 eV = 1.89 x 1.6 x 10-19 J = 3.024 x 10-19 J 1eV – 1.6 x 10-19 J h = 6.626 x 10-34 Js Light energy - ΔE = hf Frequency, f = ΔE/h Frequency, f = ΔE/h f = 3.024 x 10-19 /6.626 x 10-34 = 4.56 x 1015 Hz λ = c/f = 3 x 108/4.56 x 1015 = 657 x 10-9 = 657nm Ionization energy Transition electron from 1 ->∞ constant Light given off Light given off 1 2 3 4 5 6 1 2 3 4
- 10. Ionization Energy for Hydrogen Atom 1 2 3 4 5 ∞ Ionization energy Min energy to remove 1 mole electron from 1 mole of element in gaseous state M(g) M+ (g) + e Energy difference bet level 3 to 2 1 2 n = energy level Energy level, n= 1 = -13.6/n2 = -13.6/1 = -13.6 eV 3 4 5 Energy difference, n= 3-2 = -1.51 – (-3.4) eV = 1.89 eV = 1.89 x 1.6 x 10-19 J = 3.024 x 10-19 J Light energy - ΔE = hf Frequency, f = ΔE/h Frequency, f = ΔE/h f = 3.024 x 10-19 /6.626 x 10-34 = 4.56 x 1015 Hz λ = c/f = 3 x 108/4.56 x 1015 = 657 x 10-9 = 657nm Ionization energy Transition electron from 1 ->∞ Energy level, n= ∞ = -13.6/n2 = -13.6/∞ = o eV ∞ Energy Absorb Energy difference, n= 1-> ∞ = 0 – (-13.6) eV = 13.6 eV = 13.6 x 1.6 x 10-19 J = 2.176 x 10-18 J for 1 electron Energy absorb for 1 MOLE electron -2.176 x 10-18 J - 1 electron -2.176 x 10-18 x 6.02 x 1023 J - 1 mole -1309kJ mol-1 Light given off, electronic transition from high -> low level Energy Released Light/photon ABSORB by electron Light given off Light given off Light given off electron 1 2 3 4 5 6 1 2 3 4 5
- 11. Energy/Wavelength – Plank/Rydberg Equation ΔE = hf 1 2 3 4 5 ∞ Formula – Plank Equation Electron transition from 3 -> 2 1 2 n = energy level R = Rydberg constant R = 1.097 x 107 m-1 3 4 5 Rydberg Equation to find wavelength nf = 2, ni = 3 R = 1.097 x 107 λ = 657 x 10-9 = 657 nm Nf = final n level Ni = initial n level f = c/λ = 3 x 108/657 x 10-9 = 4.57 x 1014 Hz Energy photon- high -> low level Click here to view video Click here to view video Click here on energy calculation ∞ Energy Level/Ionization Energy Calculation Light given off Light given off Rydberg Eqn find wavelength emit 1 2 3 4 5
- 12. 1 2 3 4 5 ∞ Electron transition from 3 -> 2 1 2 n = energy level 3 4 5 nf = 2, ni = 3 R = 1.097 x 107 λ = 657 x 10-9 = 657 nm f = c/λ = 3 x 108/657 x 10-9 = 4.57 x 1014 Hz Energy photon- high -> low level ∞ Ionization Energy for Hydrogen Atom Ionization energy Min energy to remove 1 mole electron from 1 mole of element in gaseous state M(g) M+ (g) + e Ionization energy Transition electron from 1 -> ∞ Energy Absorb Rydberg Eqn find ionization energy nf = ∞, ni = 1 R = 1.097 x 107 λ = 9.11 x 10-8 Energy absorb for 1 MOLE electron -2.179 x 10-18 J - 1 electron -2.179 x 10-18 x 6.02 x 1023 J - 1 mole -1312kJ mol-1 Energy, E = hf = 6.626 x 10-34 x 3.29 x 1015 = 2.179 x 10-18 J for 1 electron f = c/λ = 3 x 108/9.11 x 10-8 = 3.29 x 1015 Hz Light/photon ABSORB by electron electron Light given off, electronic transition from high -> low level Light given off Light given off Rydberg Eqn find wavelength emit 1 1 3 4 5 6 7 1 2 3 4 5
- 13. 1 2 3 4 5 ∞ 1 2 n = energy level 3 4 5 Energy = hv (1 mole) = 6.626 x 10-34 x 32.26 x 1014 x 6.o2 x 1023 = 1312KJ mol-1 ∞ Light/photon ABSORB by electron electron 6 6 7 7 8 8 Calculating Ionization Energy from Lyman Series ( n = 1 to ∞ ) Excited energy level Frequency, v / x 1014 s-1 ΔV / x 1014 s-1 2 24.66 4.57 3 29.23 1.60 4 30.83 0.74 5 31.57 0.40 6 31.97 0.24 7 32.21 0.16 8 32.37 Line spectrum converge (get closer) with increase freq Ionization energy determined from (Limit of convergence) Ionization energy Transition electron from 1 ->∞ Ionization energy Transition electron from 1 ->∞ Difference bet freq successive lines Find freq v, at which it converge Δv = 0 Δv = 0 Plot graph v against Δv Find Ionization Energy 1 2 3 Linear curve fit equation Δv = -0.5897v + 19.022 4 Freq, v when Δv = 0 -0.5897v + 19.022 = 0 v = 19.022 x 1014 s-1 0.5897 v = 32.26 x 1014s-1 5 Question adapted from Pearson
- 14. 1 2 3 4 5 ∞ 1 2 n = energy level 3 4 5 Energy = hv (1 mole) = 6.626 x 10-34 x 32.86 x 1014 x 6.o2 x 1023 = 1312KJ mol-1 Energy for n level: ∞ 6 6 7 7 8 8 Calculating Ionization Energy from Lyman Series ( n = 1 to ∞ ) Excited energy level, n Excited energy level, 1/n2 Frequency V / x 1014 s-1 2 0.25 24.66 3 0.11 29.23 4 0.0625 30.83 5 0.04 31.57 6 0.027 31.97 7 0.02 32.21 8 0.015 32.37 Find freq v, when 1/n2 = 0 Plot graph v against 1/n2 1 Find Ionization Energy 2 3 Linear curve fit equation v = -32.84 (1/n2) + 32.86 4 Freq, v when 1/n2 = 0 v = -32.84 (1/n2) + 32.86 v = 32.86 x 1014 s-1 5 Question adapted from Pearson 2 13.6 n E E hv 2 13.6 n hv 2 13.6 hn v c h n v 2 13.6 1 Plot graph v against 1/n2
- 15. Continuous Spectrum Light spectrum with all wavelength/frequency Emission Line Spectrum • Spectrum with discrete wavelength/ frequency • Excited electrons drop from higher to lower energy level Continuous Spectrum Vs Line Spectrum Click here spectrum for diff elements Click here spectrum for diff element Click here on quantum mechanic, structure of atom Click here to view excellent simulation Click here to view simulation Excellent simulation on emission spectrum Emission line spectrum for different elements Click here to view simulation Video on quantum mechanics
