Downloaded 67 times
Uploaded byWestley Field
Cosine and sine_rule
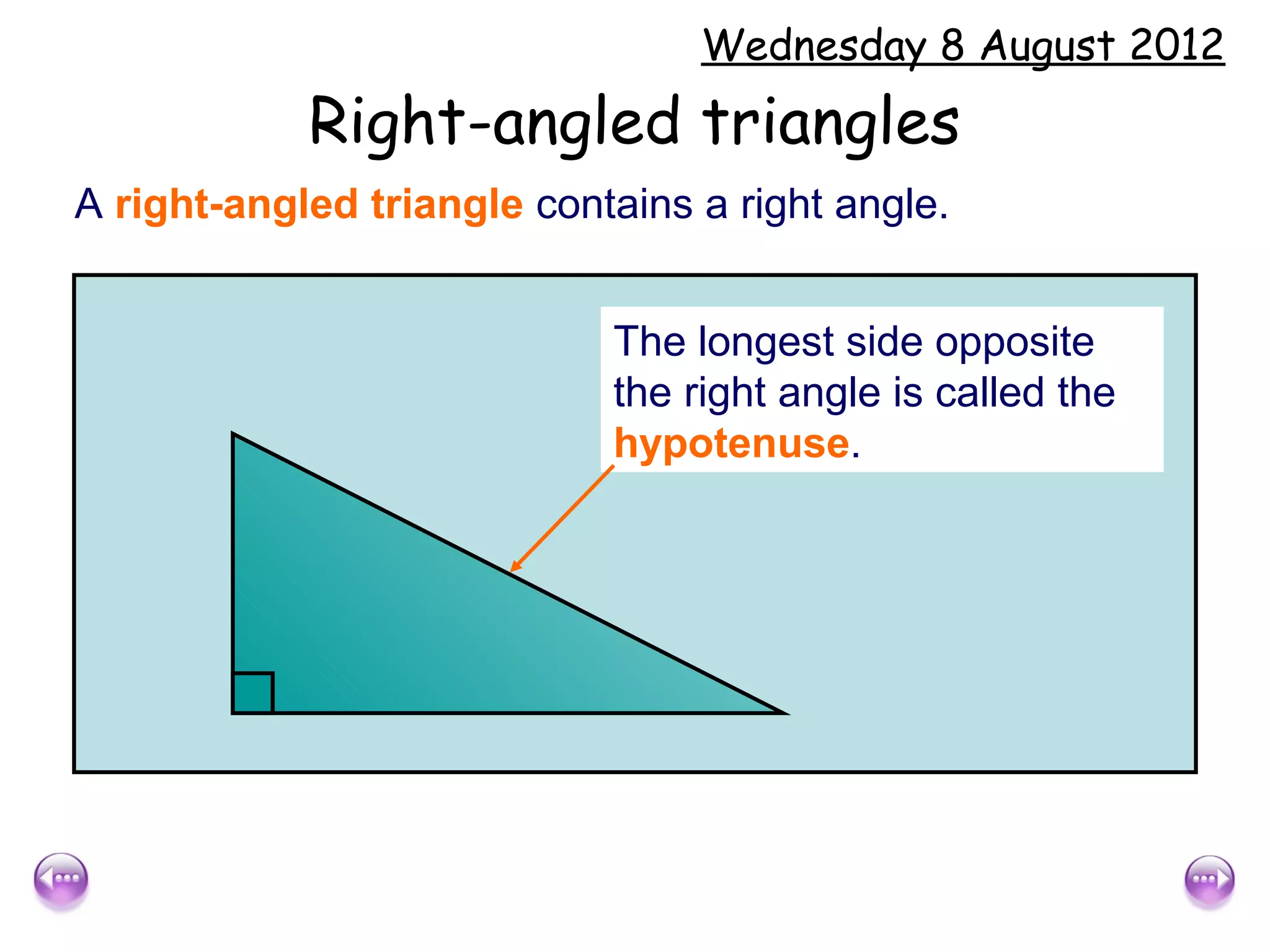
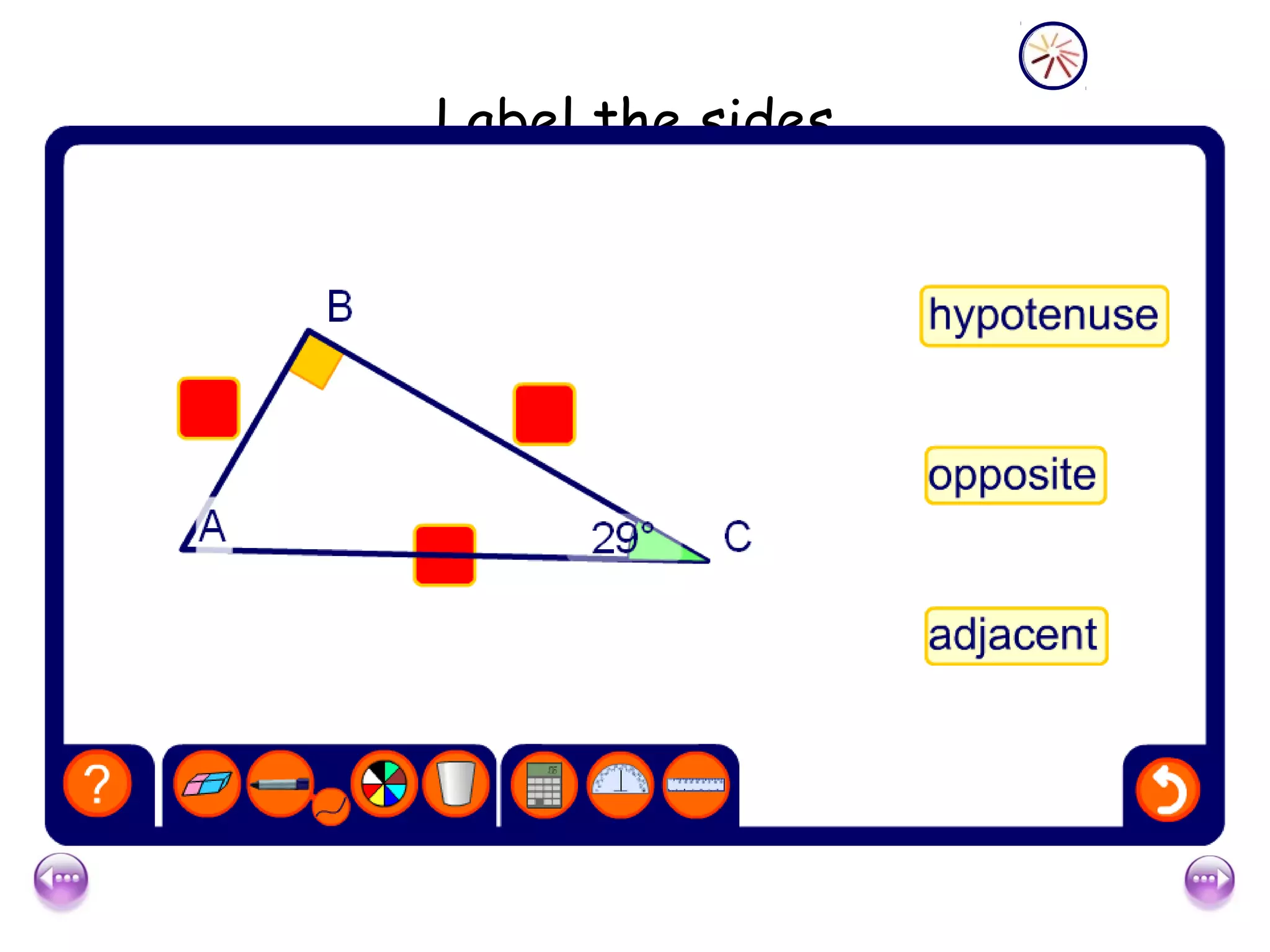
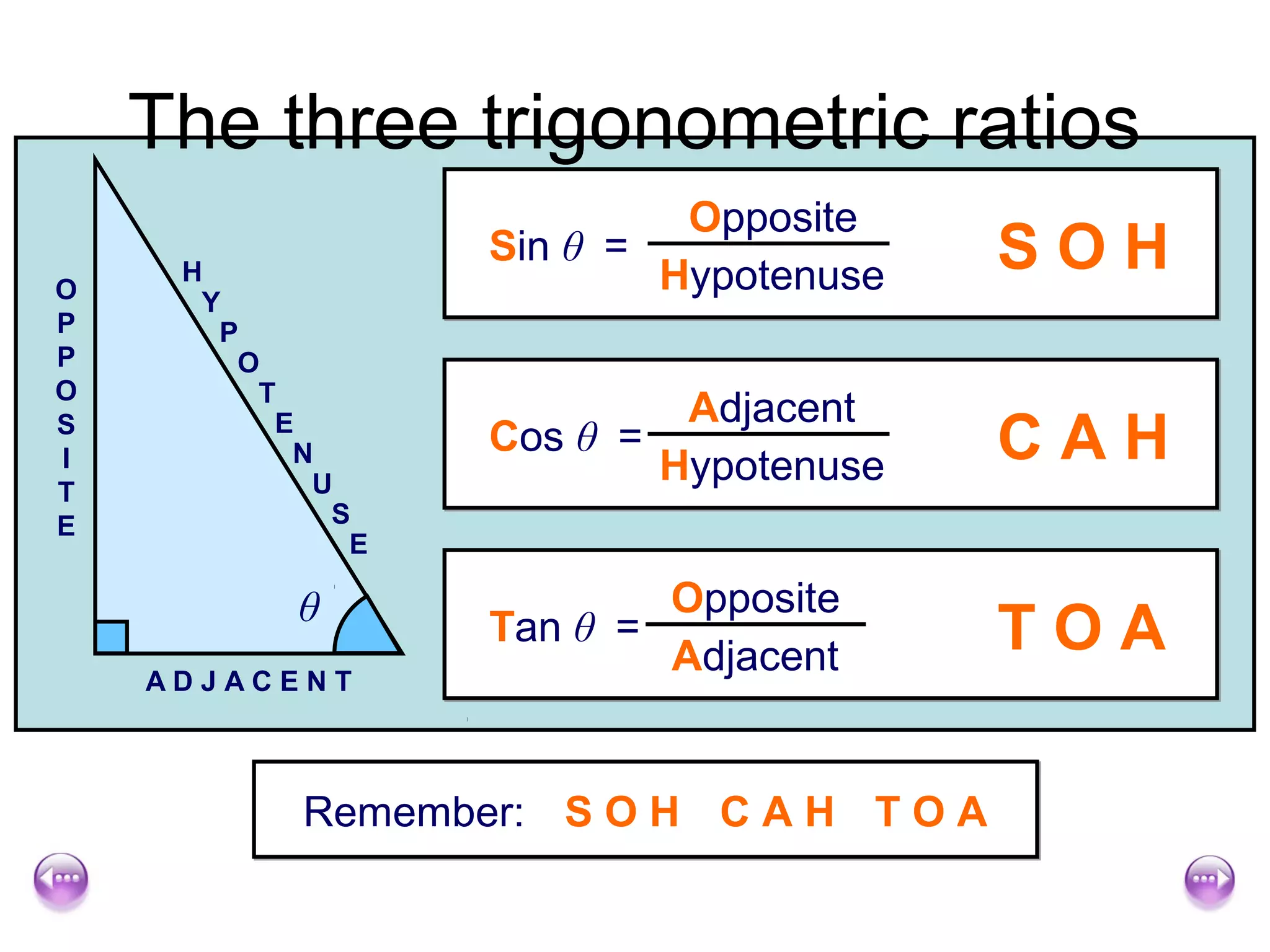
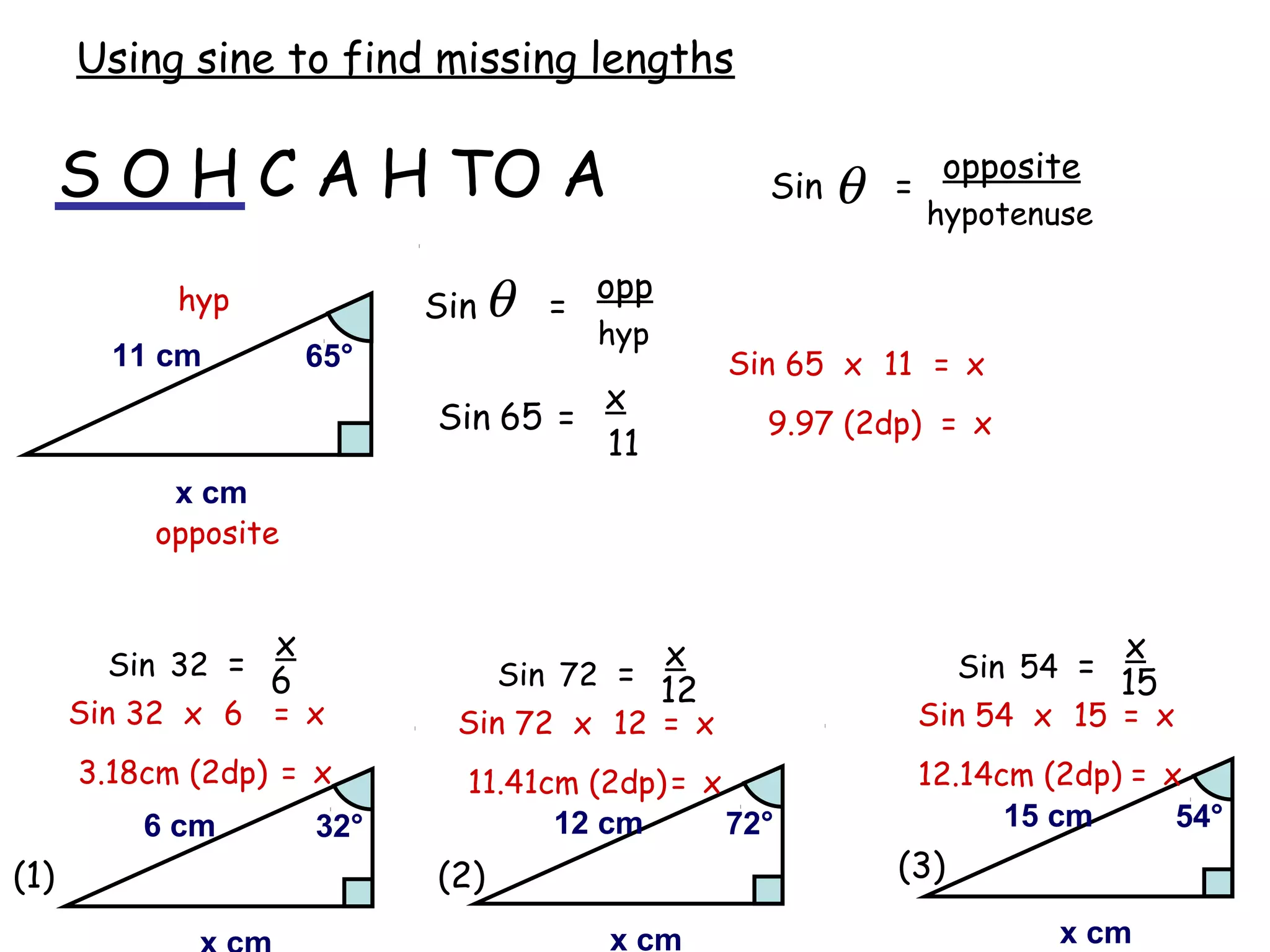
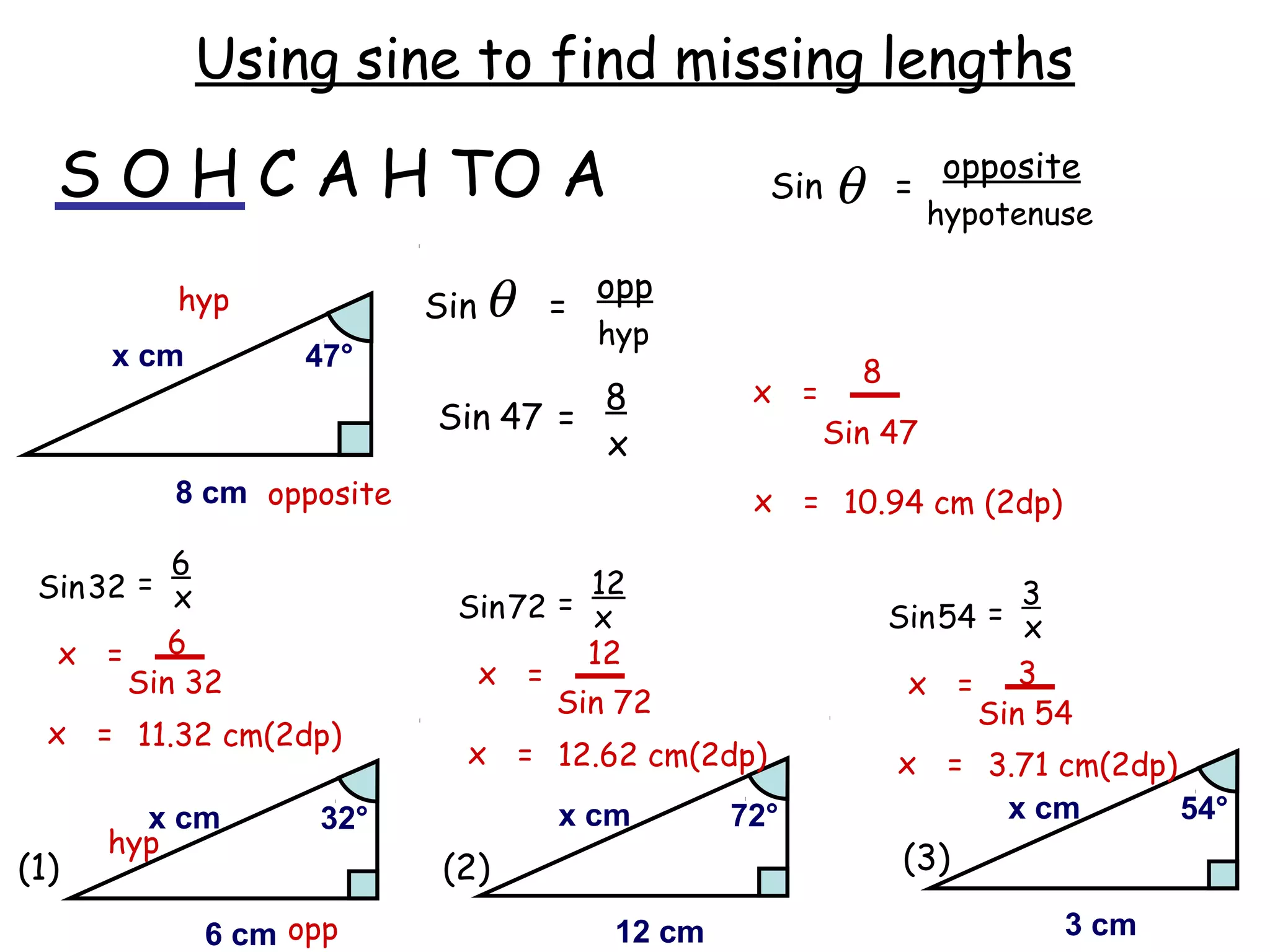
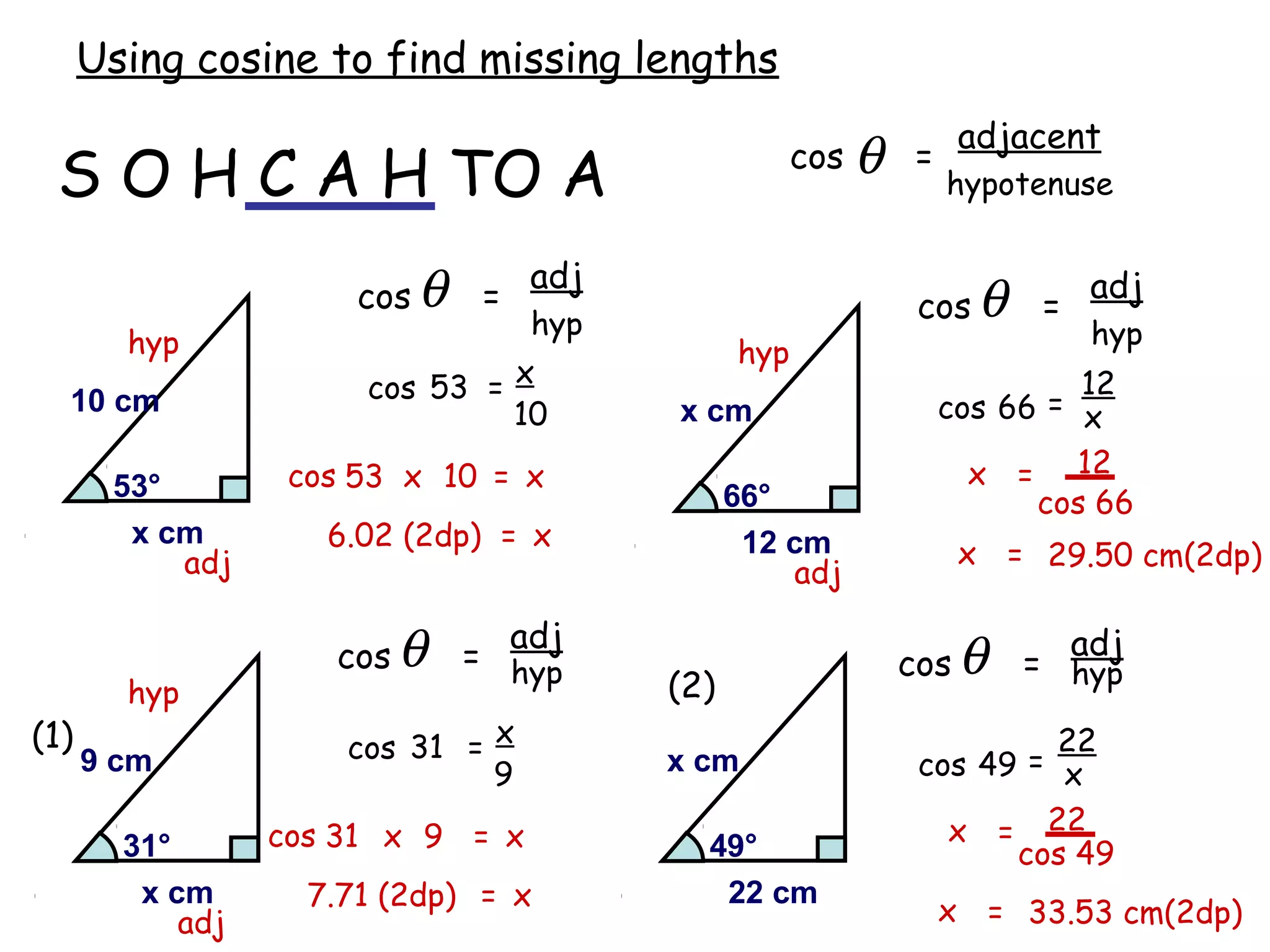
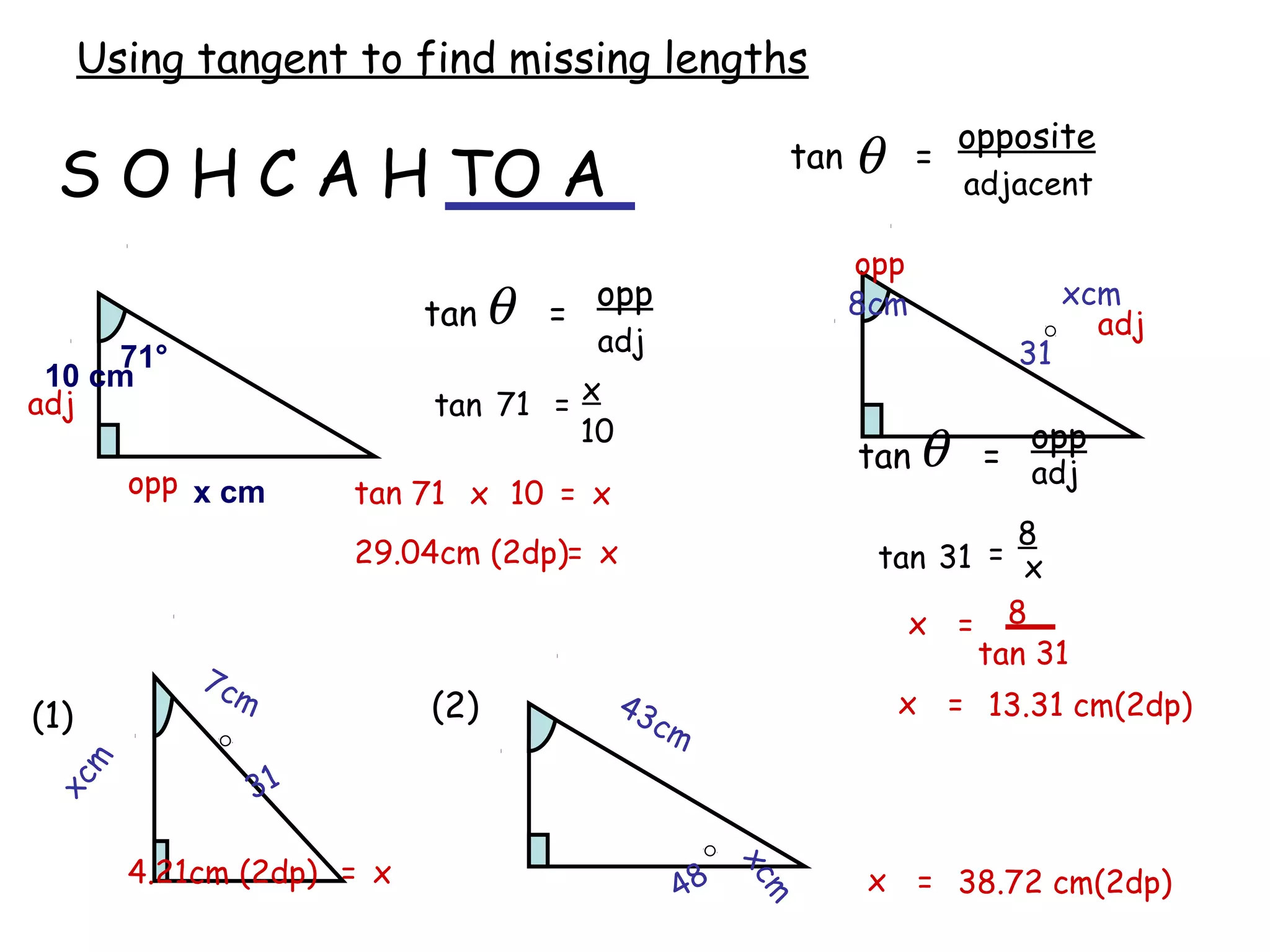
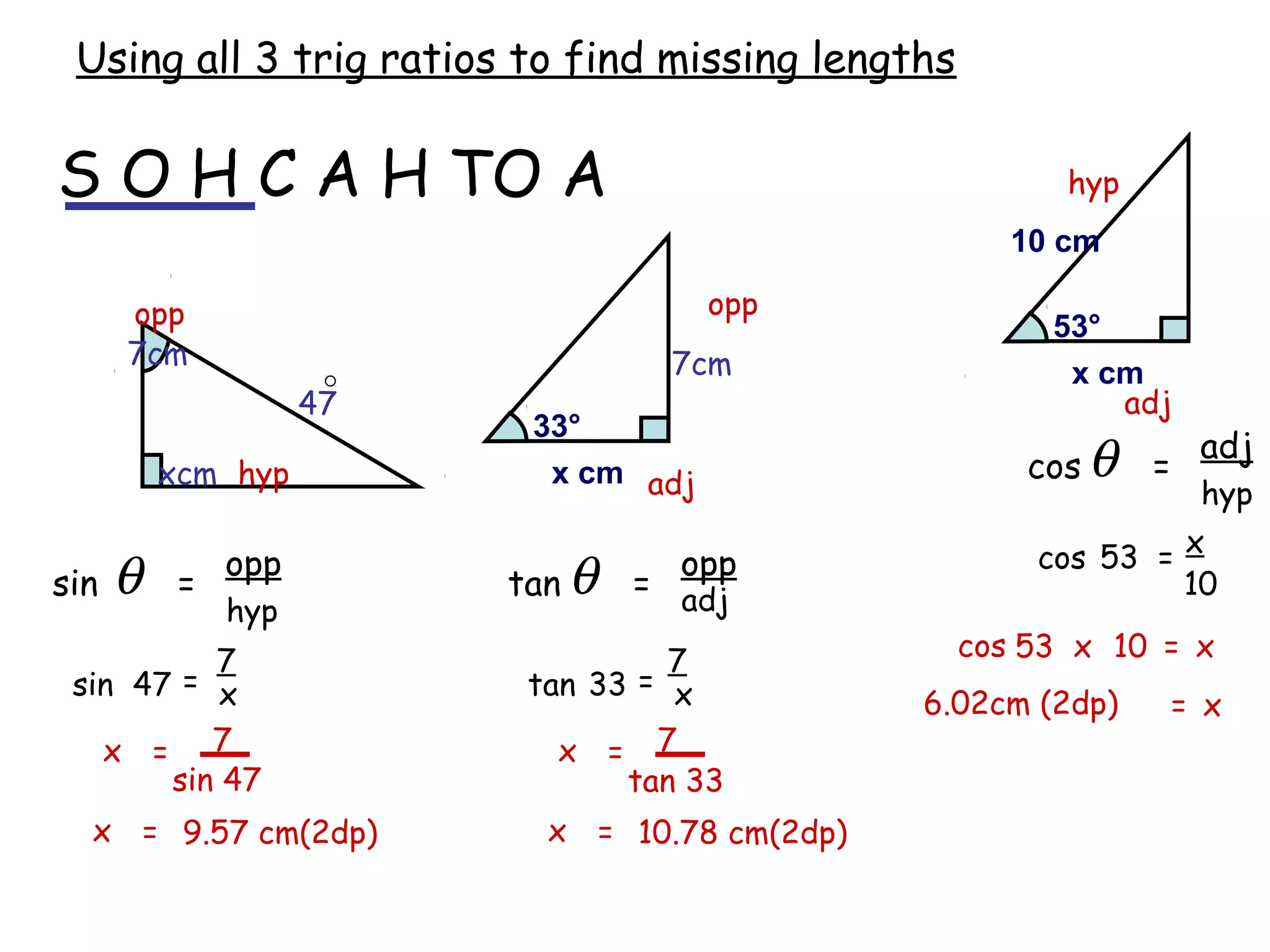
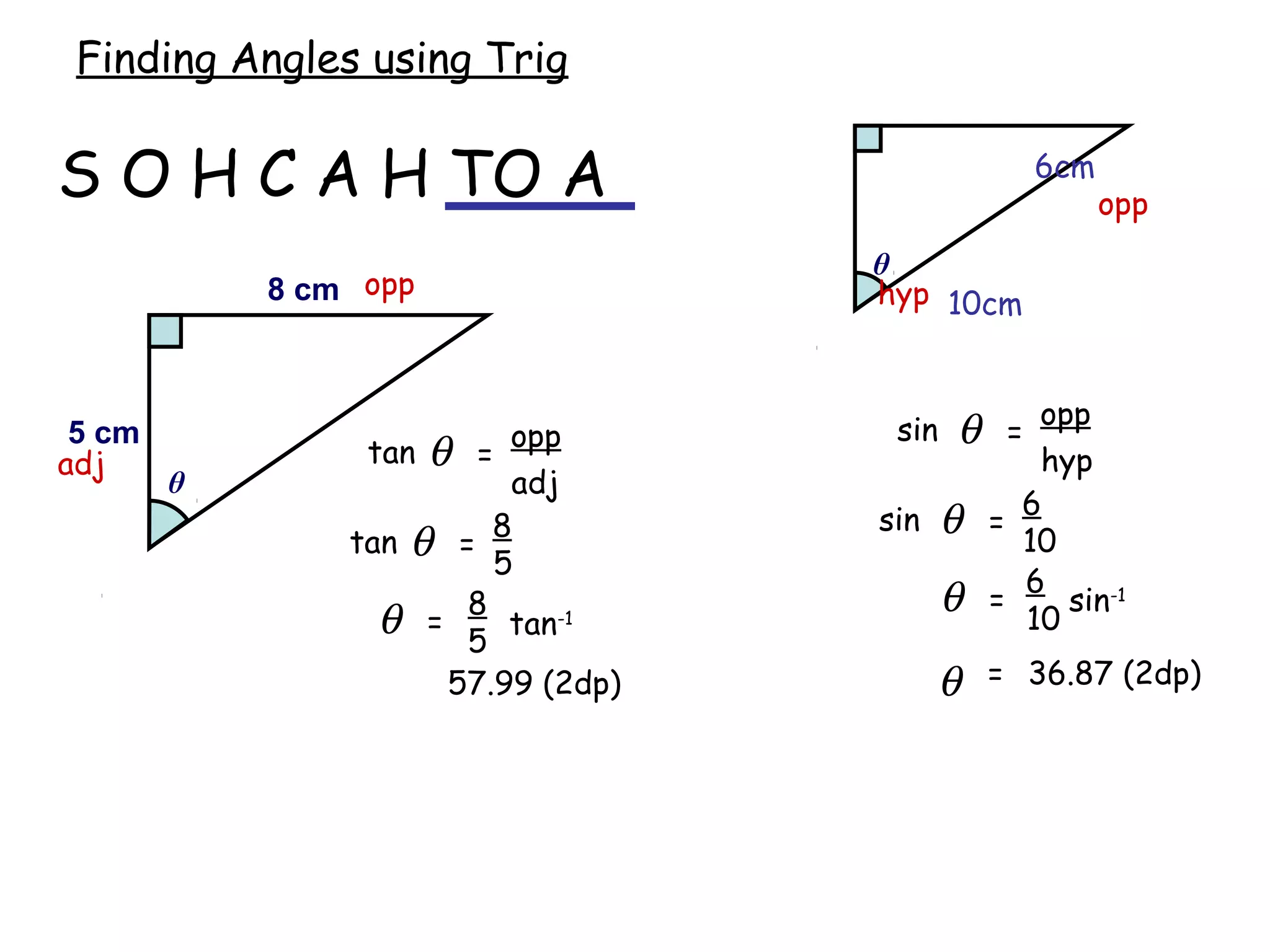
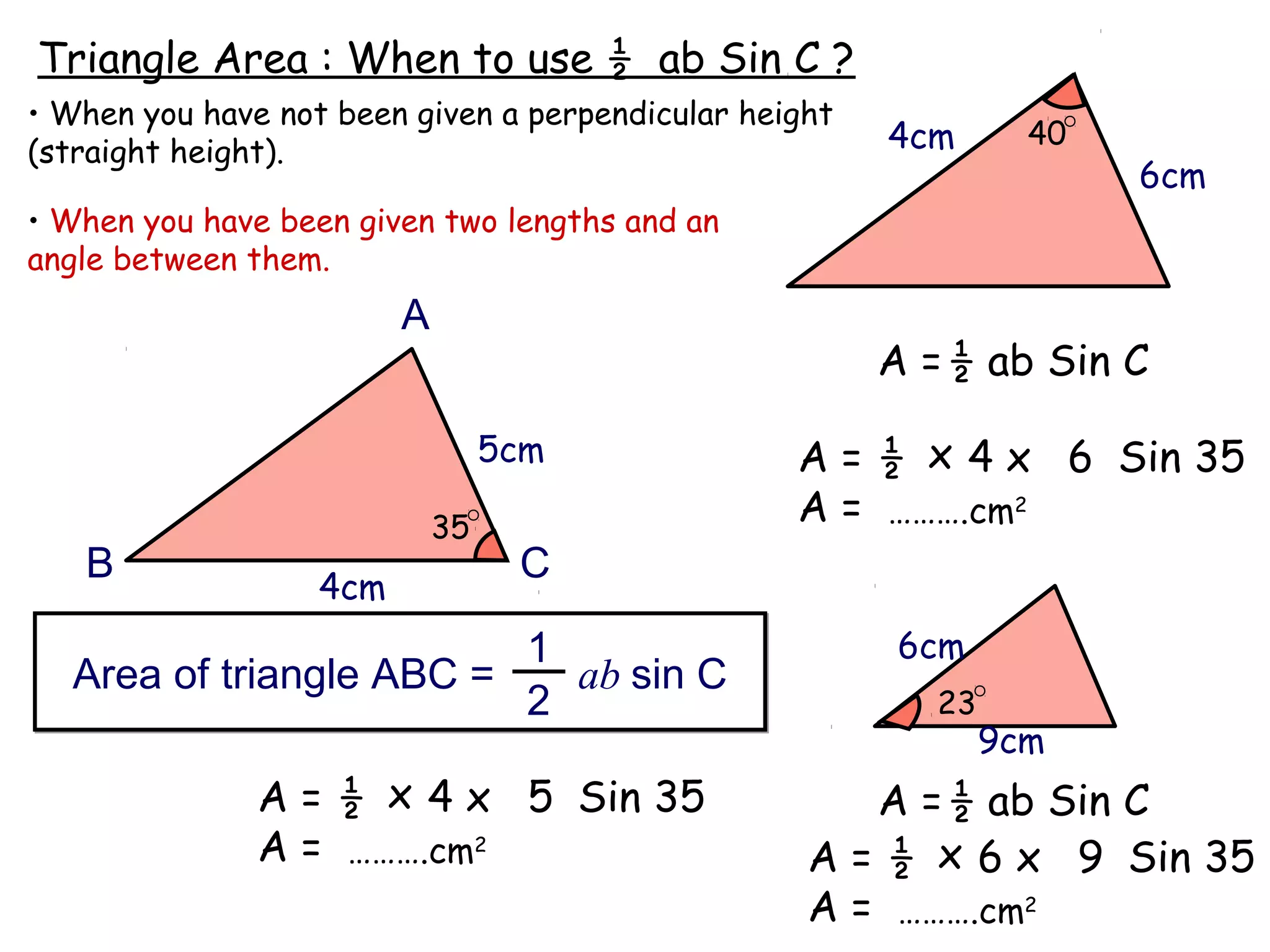
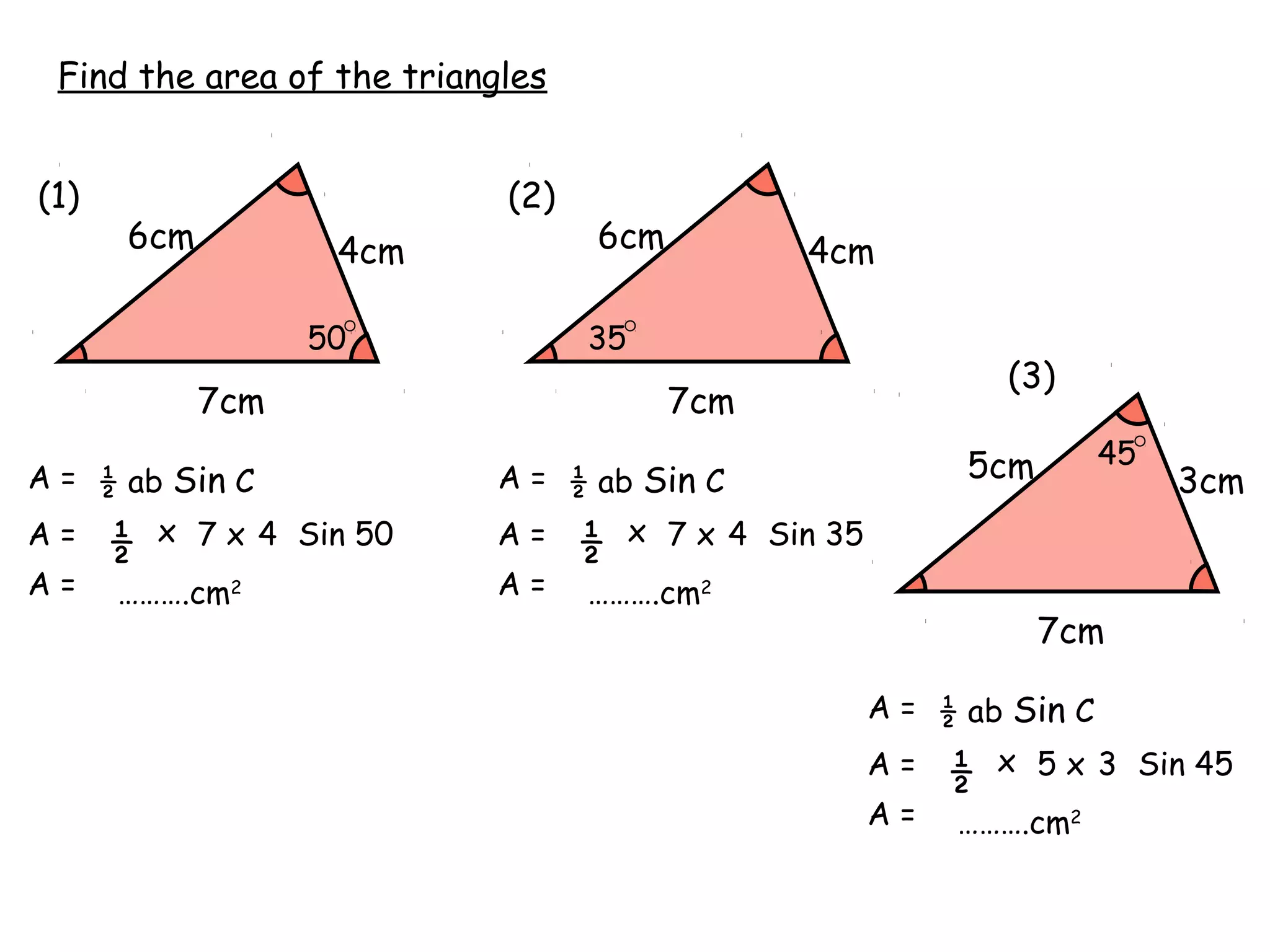
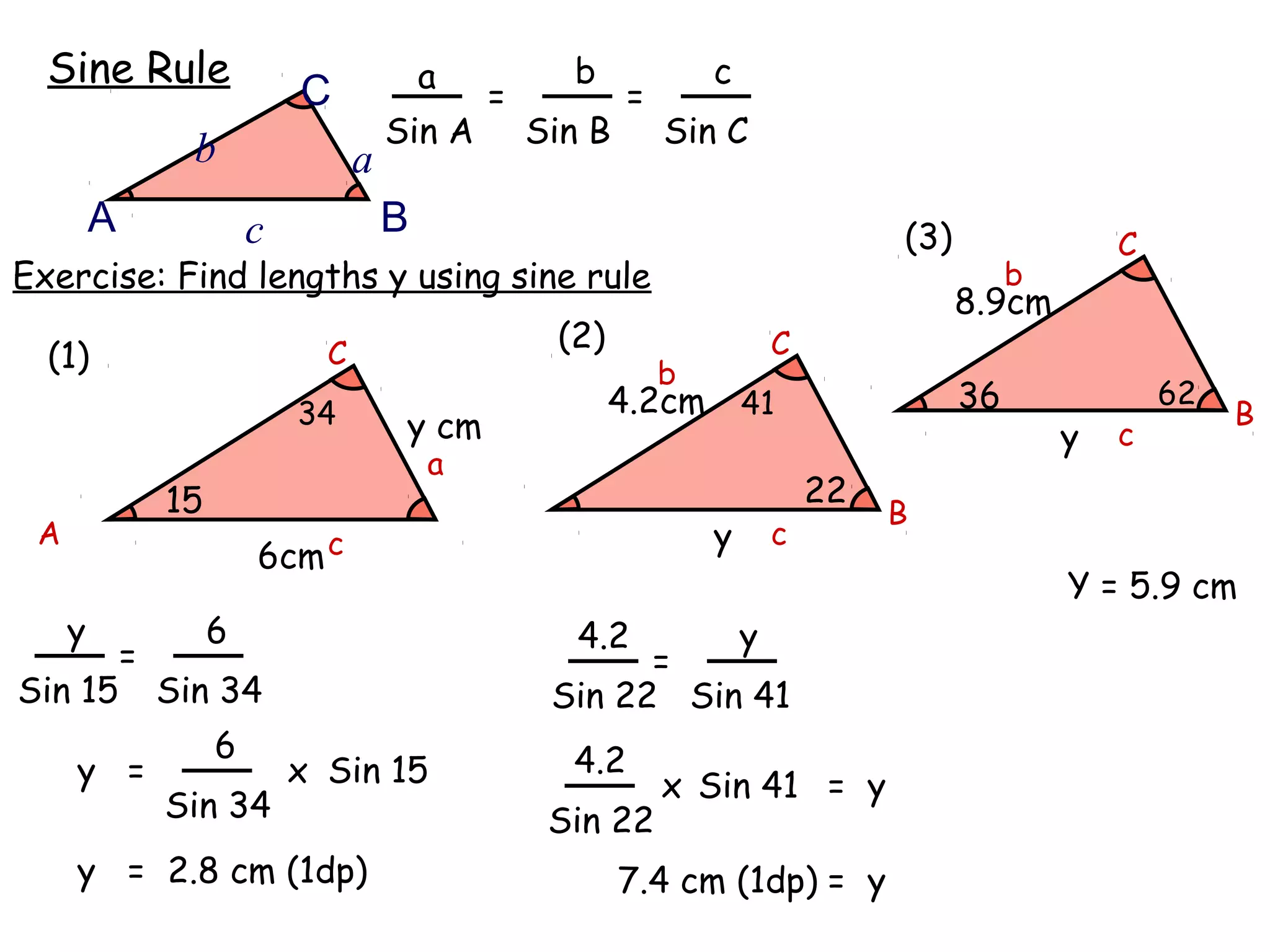
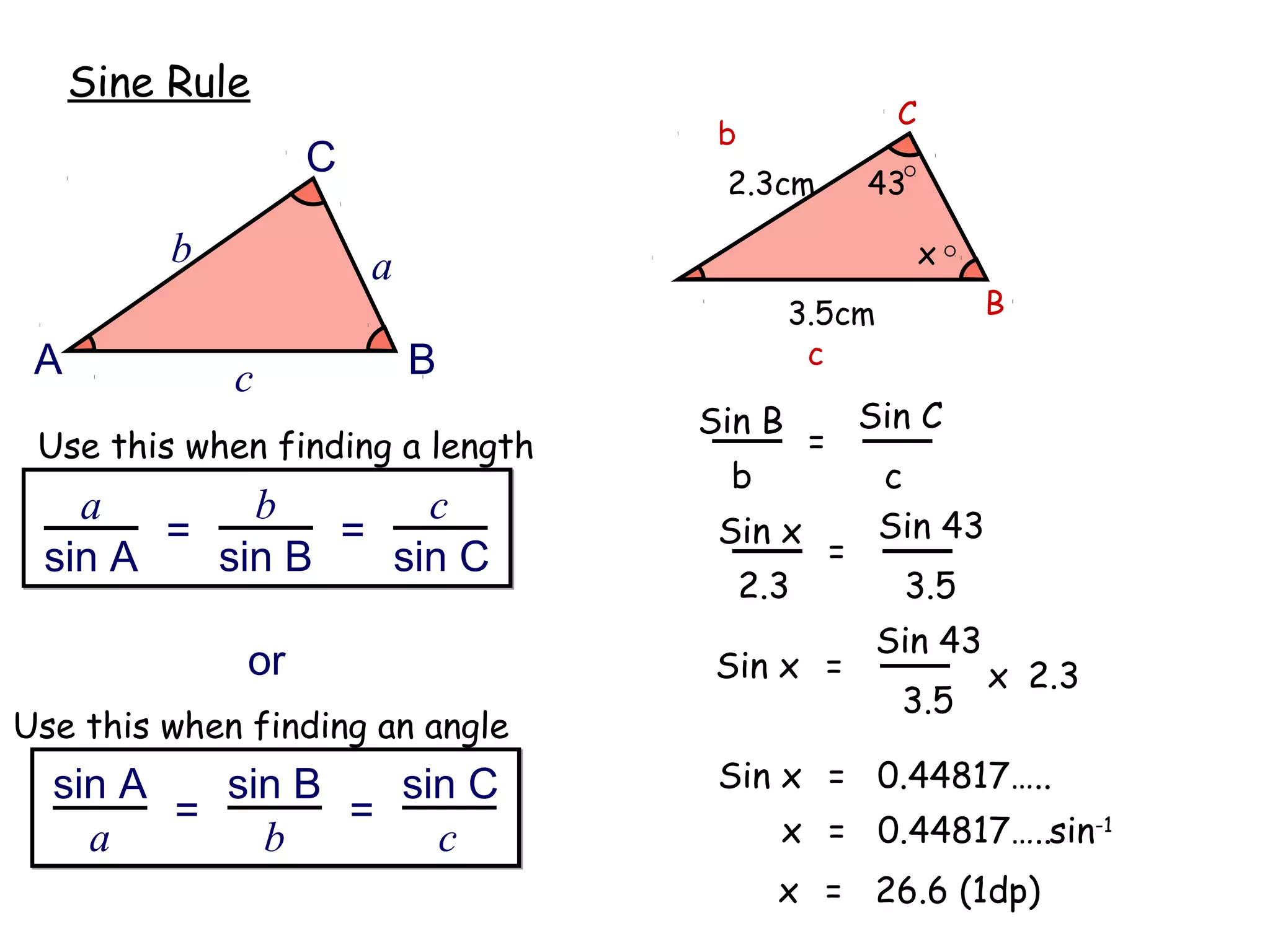
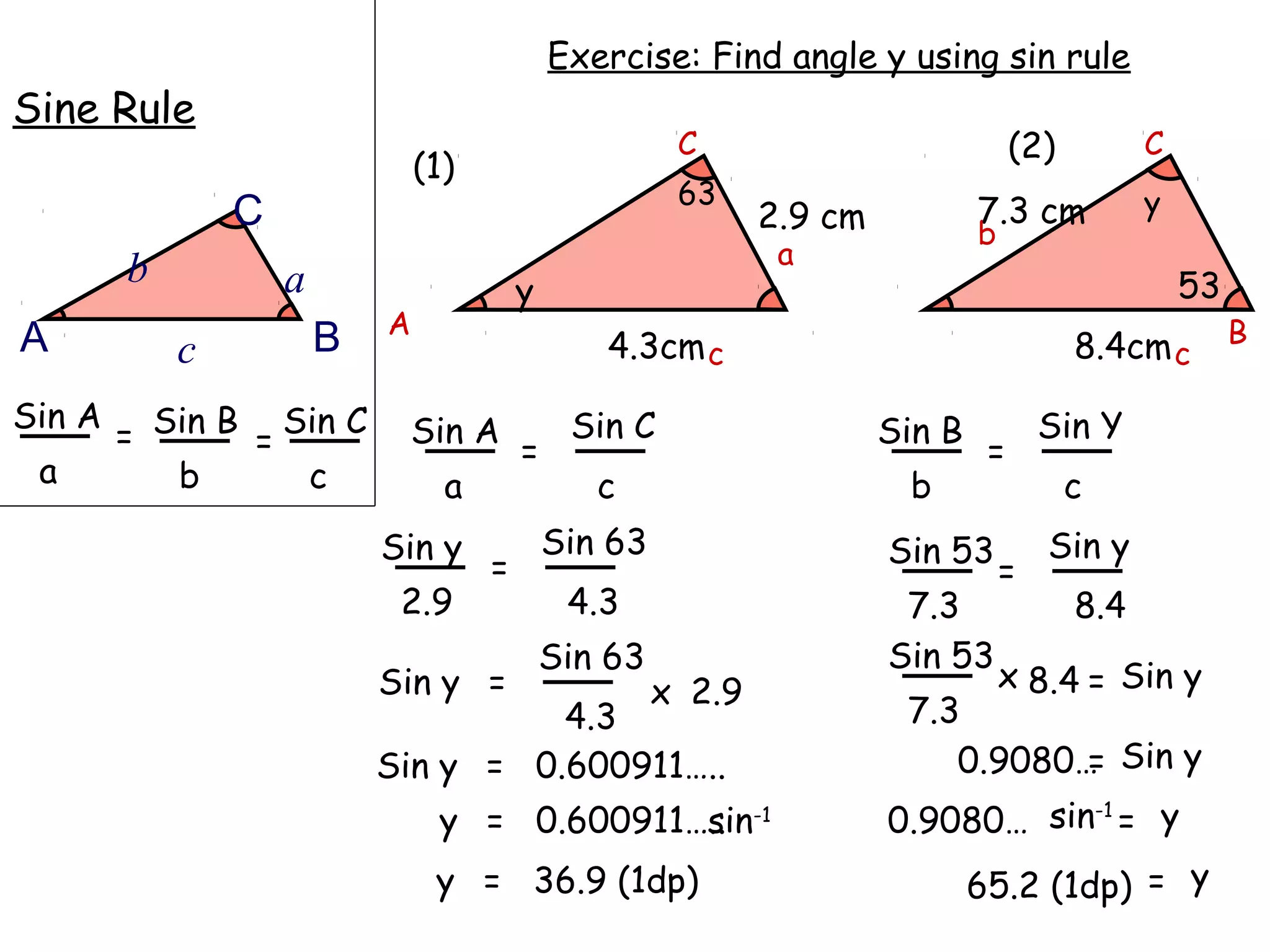
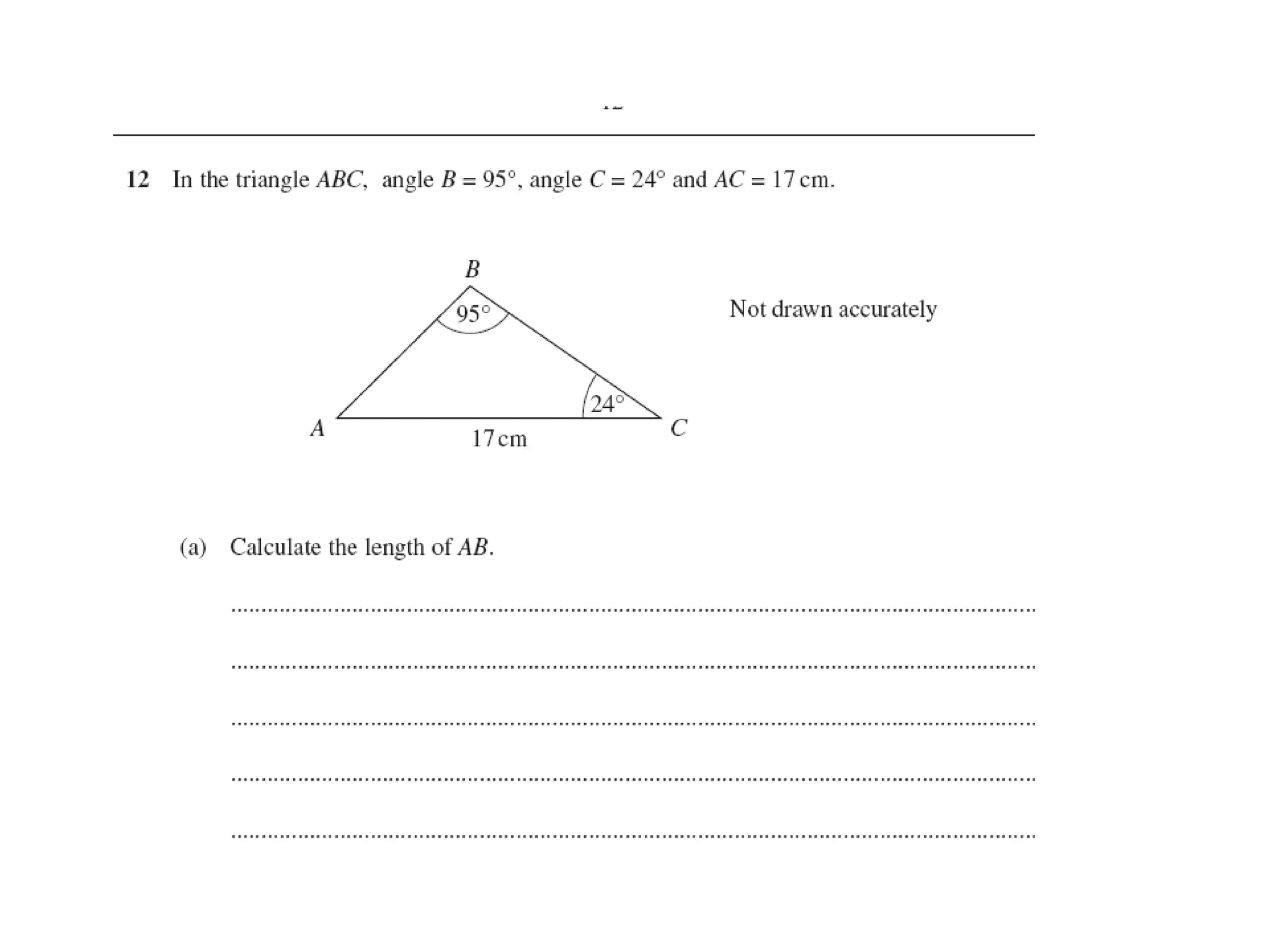
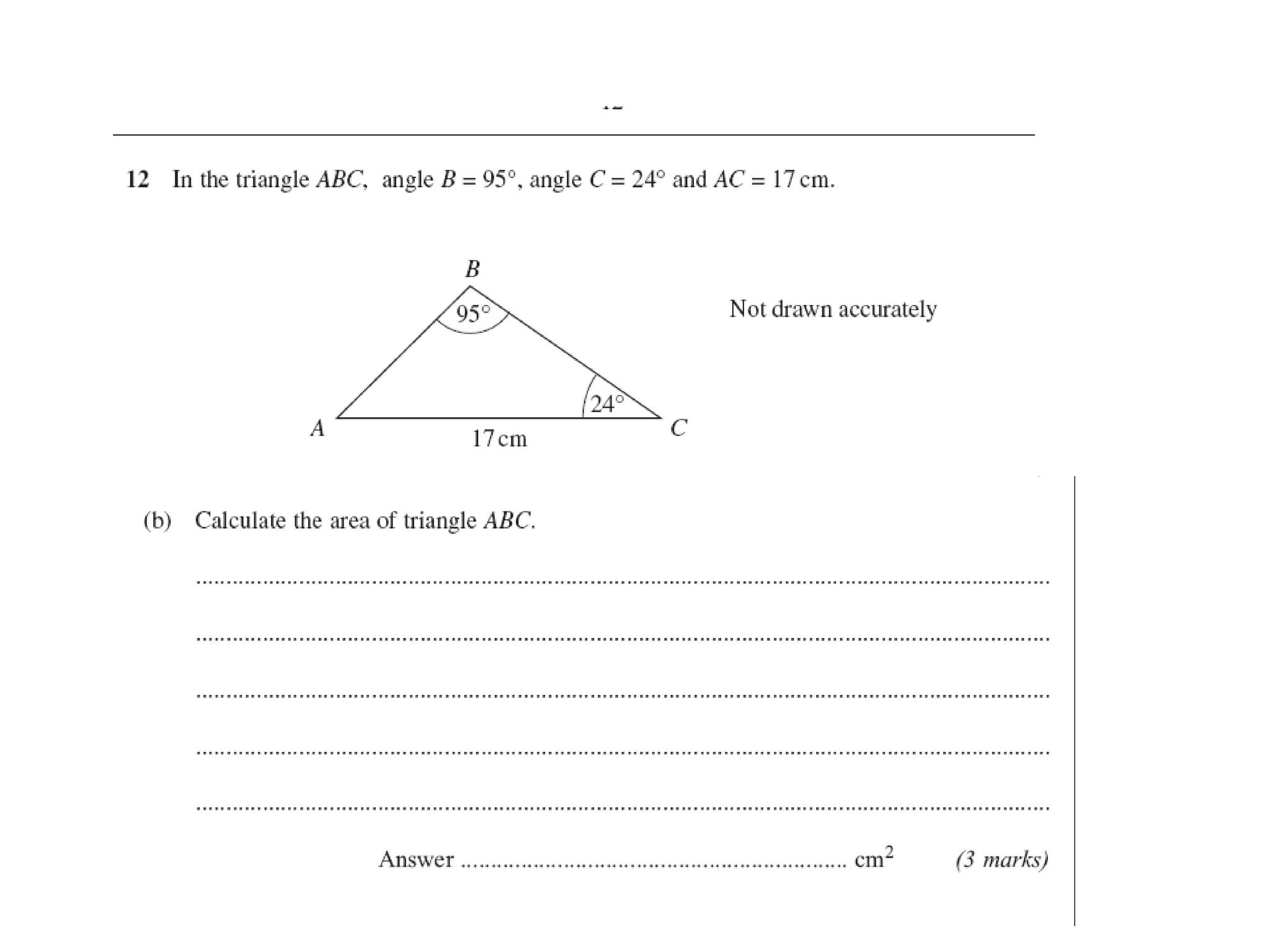
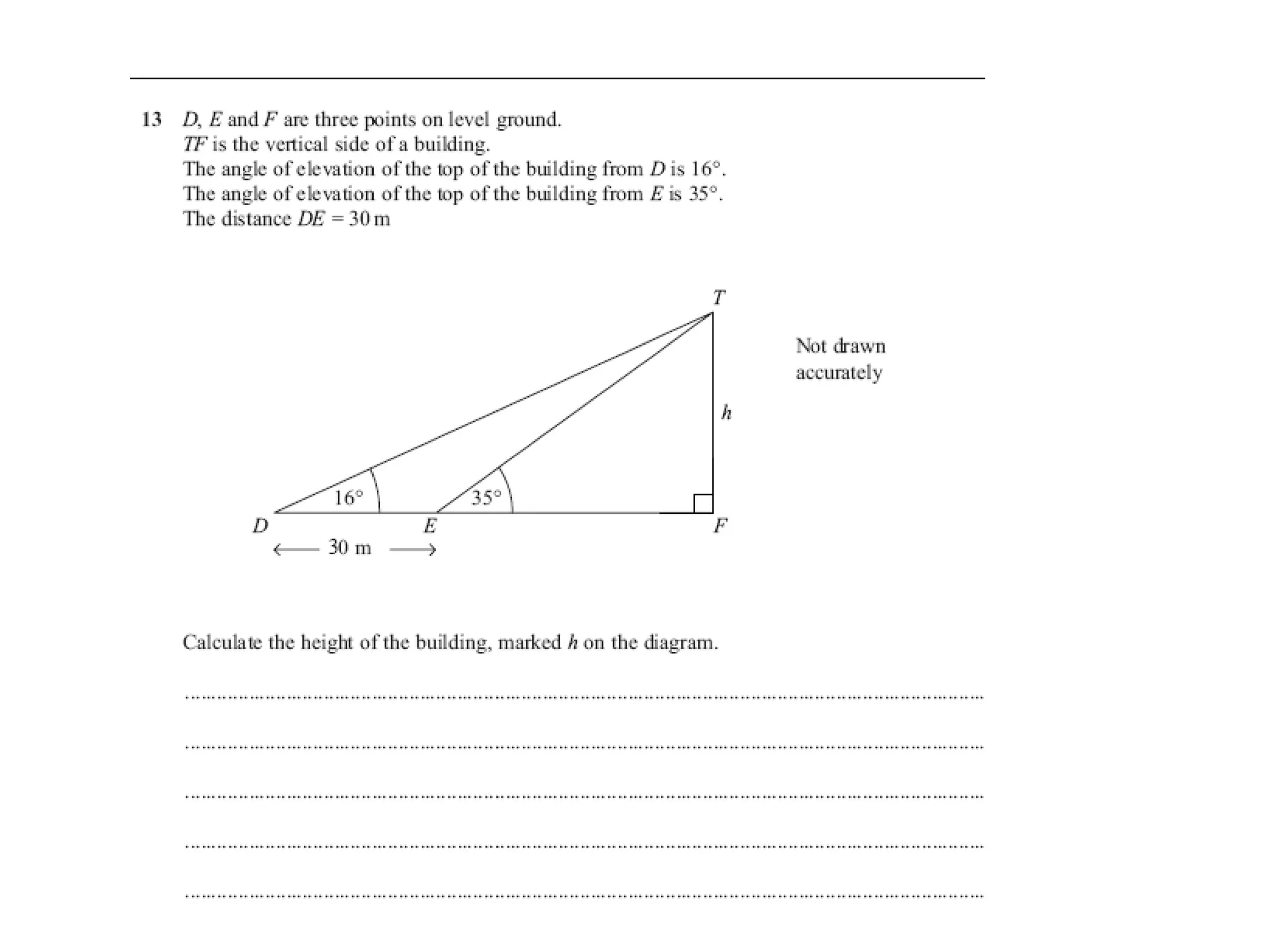
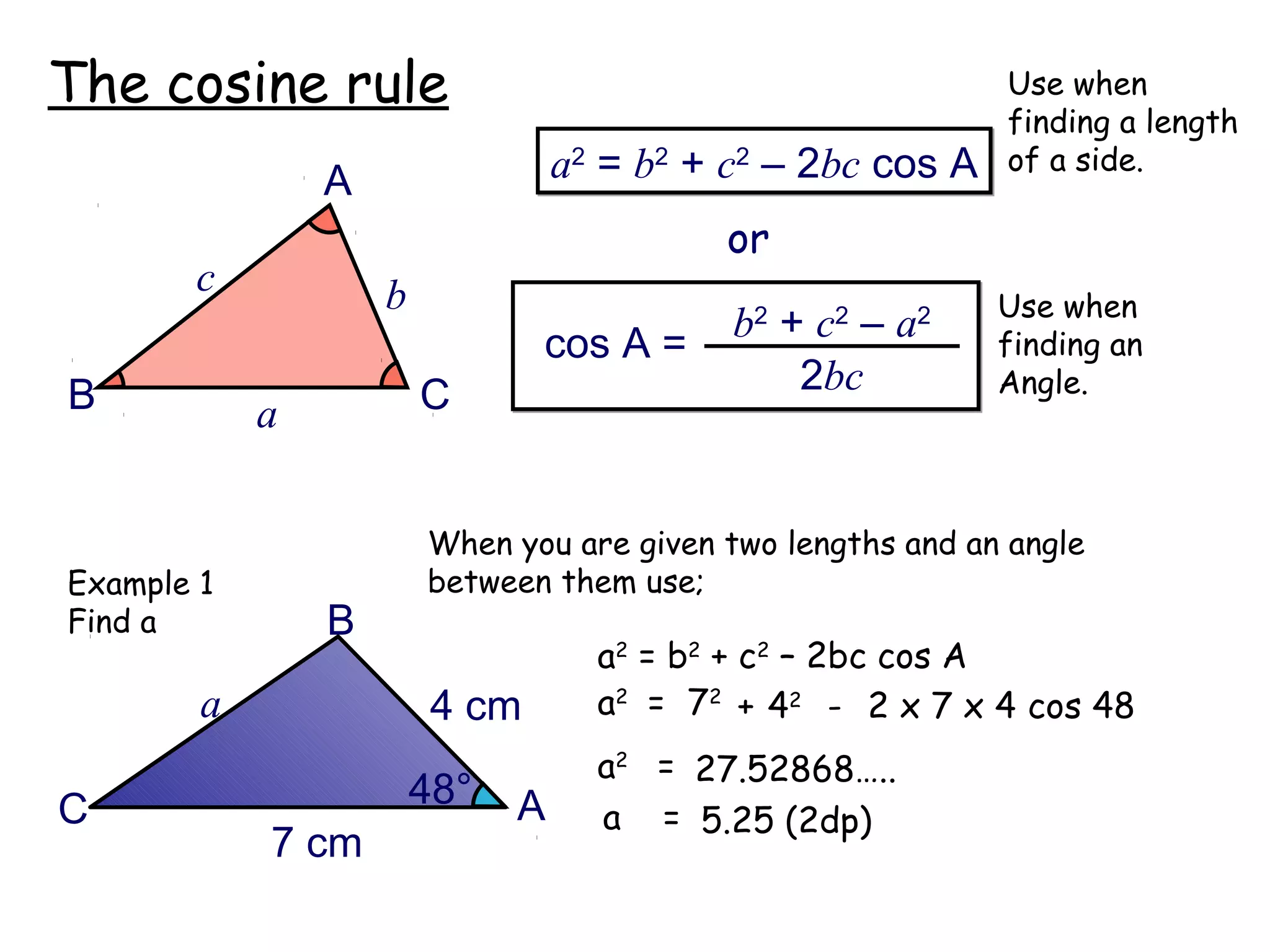
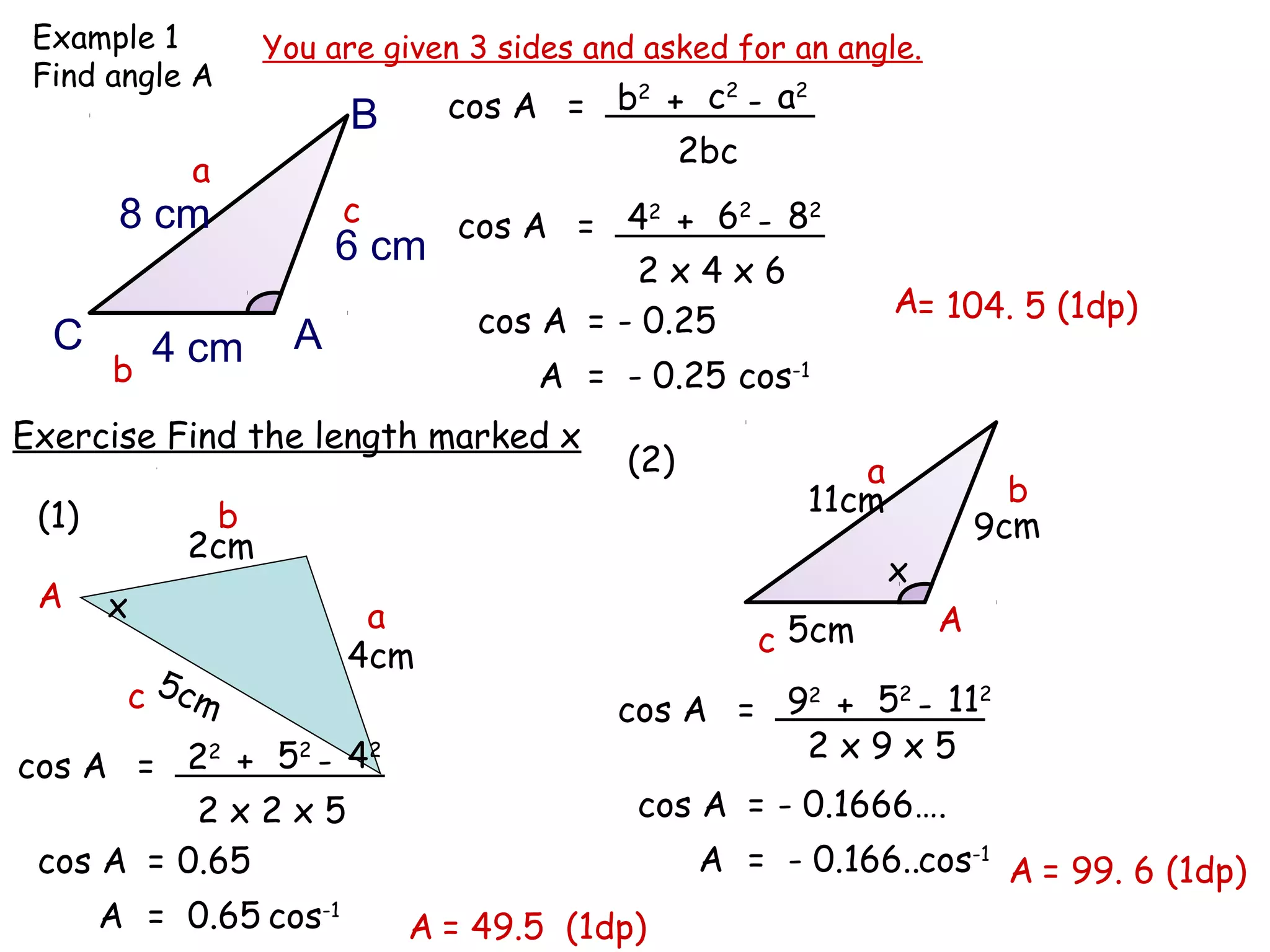
The document discusses using trigonometric ratios (sine, cosine, tangent) to find missing lengths and angles in right-angled triangles. It provides examples of using sine to find the opposite side when given the hypotenuse and angle, using cosine to find the adjacent side, and using tangent to find the opposite side when given the adjacent side and angle. The key trigonometric ratios SOH CAH TOA (sine=opposite/hypotenuse, cosine=adjacent/hypotenuse, tangent=opposite/adjacent) are explained. Worked examples are provided to demonstrate using each ratio to calculate missing sides of triangles.
More Related Content
Cosine and sine_rule
- 1. Wednesday 8 August2012 Trigonometry Using all 3 trig ratios to find missing lengths Outcomes Must: Use label sides of triangles correctly Should: Be able to do calculations involving trig functions Could: Use trig ratios to find missing lengths in triangles.
- 2. Wednesday 8 August2012 Right-angled triangles A right-angled triangle contains a right angle. The longest side opposite the right angle is called the hypotenuse.
- 3. The opposite andadjacent sides The two shorter sides of a right-angled triangle are named with respect to one of the acute angles. The side opposite the marked angle is called the opposite side. The side between the x marked angle and the right angle is called the adjacent side.
- 4.
- 5. Calculate the followingratios Use your calculator to find the following to 3 significant figures. 1) sin 79° = 0.982 2) cos 28° = 0.883 3) tan 65° = 2.14 4) cos 11° = 0.982 5) sin 34° = 0.559 6) tan 84° = 9.51 7) tan 49° = 1.15 8) sin 62° = 0.883 9) tan 6° = 0.105 10) cos 56° = 0.559
- 6. The three trigonometricratios Opposite O H Sin θ = Hypotenuse SOH Y P P P O O T Adjacent S I E N Cos θ = Hypotenuse CAH T U E S E θ Opposite Tan θ = Adjacent TOA ADJACENT Remember: S O H C A H T O A
- 7. The sine ratio the length of the opposite side The ratio of is the sine ratio. the length of the hypotenuse The value of the sine ratio depends on the size of the angles in the triangle. O H P Y P We say: P O T O E opposite S N U sin θ = I S E hypotenuse T E θ
- 8. Using sine tofind missing lengths S O H C A H TO A Sin θ = opposite hypotenuse opp hyp Sin θ = hyp 11 cm 65° Sin 65 x 11 = x x Sin 65 = 9.97 (2dp) = x 11 x cm opposite x x x Sin 32 = Sin 72 = Sin 54 = 6 12 15 Sin 32 x 6 = x Sin 72 x 12 = x Sin 54 x 15 = x 3.18cm (2dp) = x 11.41cm (2dp) = x 12.14cm (2dp) = x 6 cm 32° 12 cm 72° 15 cm 54° (1) (2) (3) x cm x cm
- 9. Using sine tofind missing lengths S O H C A H TO A Sin θ = opposite hypotenuse opp hyp Sin θ = hyp x cm 47° 8 8 x = Sin 47 = Sin 47 x 8 cm opposite x = 10.94 cm (2dp) 6 Sin 32 = x 12 3 Sin 72 = x Sin 54 = x x = 6 12 Sin 32 x = x = 3 Sin 72 Sin 54 x = 11.32 cm(2dp) x = 12.62 cm(2dp) x = 3.71 cm(2dp) x cm 32° x cm 72° x cm 54° hyp (1) (2) (3) 6 cm opp 12 cm 3 cm
- 10. Using cosine tofind missing lengths adjacent cos θ = S O H C A H TO A hypotenuse adj cos θ = cos θ = adj hyp hyp hyp hyp cos 53 = x 12 10 cm 10 x cm cos 66 = x 53° cos 53 x 10 = x x = 12 66° cos 66 x cm 6.02 (2dp) = x 12 cm adj x = 29.50 cm(2dp) adj adj cos θ = hyp cos θ adj = hyp hyp (2) (1) cos 31 = x 22 9 cm 9 x cm cos 49 = x 31° cos 31 x 9 = x 49° x = 22 cos 49 x cm 7.71 (2dp) = x 22 cm x = 33.53 cm(2dp) adj
- 11. Using tangent tofind missing lengths opposite S O H C A H TO A tan θ = adjacent opp opp tan θ 8cm xcm = adj adj 31 71° 10 cm adj tan 71 = x 10 opp tan θ = adj opp x cm tan 71 x 10 = x 8 29.04cm (2dp)= x tan 31 = x x = 8 tan 31 7c m (2) 43 x = 13.31 cm(2dp) (1) c m m 31 xc 4.21cm (2dp) = x 48 x = 38.72 cm(2dp) xc m
- 12. Using all 3trig ratios to find missing lengths S O H C A H TO A hyp 10 cm opp opp 53° 7cm 7cm x cm 47 adj 33° adj xcm hyp x cm adj cos θ = hyp opp opp cos 53 = x sin θ = tan θ = adj 10 hyp 7 7 cos 53 x 10 = x sin 47 = x tan 33 = x 6.02cm (2dp) = x x = 7 x = 7 sin 47 tan 33 x = 9.57 cm(2dp) x = 10.78 cm(2dp)
- 13. Finding Angles usingTrig S O H C A H TO A 6cm opp θ 8 cm opp hyp 10cm opp 5 cm tan θ = opp sin θ = adj hyp θ adj 6 tan θ = 8 sin θ = 10 5 6 θ = sin-1 θ = 8 tan-1 5 10 57.99 (2dp) θ = 36.87 (2dp)
- 15. Wednesday 8 August2012 Trigonometry 2 Objective: Use trig to find missing lengths and angles in right angled triangles for worded questions. Grade A Outcomes Must: Use trig ratios to find missing lengths and angles in triangles. Should: Use trig to answer worded problems. Could: Use trig to answer more difficult worded problems.
- 16. Finding side lengths A5 m long ladder is resting against a wall. It makes an angle of 70° with the ground. What is the distance between the base of the ladder and the wall? We are given the hypotenuse and we want to find the length of the side adjacent to 5m the angle, so we use: adjacent cos θ = hypotenuse 70° x x cos 70° = 5 x = 5 × cos 70° = 1.71 m (to 2d.p.)
- 18. Wednesday 8 August2012 Area of a triangle (using ½ ab Sin C) Outcomes Must: Understand when you Objective can use this formula for Find the area of a triangle area. triangle using Area = ½ ab sin C Should: Be able to find the area of a triangle using ½ ab sin C. Could: Answer exam questions
- 19. Triangle Area :When to use ½ ab Sin C ? • When you have not been given a perpendicular height (straight height). 4cm 40 6cm • When you have been given two lengths and an angle between them. A A = ½ ab Sin C 5cm A = ½ x 4 x 6 Sin 35 35 A = ……….cm2 B C 4cm 1 6cm Area of triangle ABC = ab sin C 2 23 9cm A = ½ x 4 x 5 Sin 35 A = ½ ab Sin C A = ……….cm2 A = ½ x 6 x 9 Sin 35 A = ……….cm2
- 20. Find the areaof the triangles (1) (2) 6cm 4cm 6cm 4cm 50 35 (3) 7cm 7cm 5cm 45 A = ½ ab Sin C A = ½ ab Sin C 3cm A= ½ x 7 x 4 Sin 50 A= ½ x 7 x 4 Sin 35 A= ……….cm2 A= ……….cm2 7cm A = ½ ab Sin C A= ½ x 5 x 3 Sin 45 A= ……….cm2
- 22. Wednesday 8 August2012 Sine Rule Outcomes Objective Use sine rule to find angles and lengths in Must: Use sine rule to find triangles. (not right lengths in triangles. angles triangles) Should: Use sine rule to find angles in triangles. Could: Answer mixed questions
- 23. Sine Rule Examples: Find y using sine rule • Find the sides and angles of a triangle whether it’s a right angle or not. b 6cm C y cm a 25 40 A B b a a b = Sin A Sin B A B y c 3 = Sin 25 Sin 40 a b c = = 3 sin A sin B sin C x Sin 40 = y Sin 25 4.56 cm (2dp) = y
- 24. Sine Rule a b c C = = Sin A Sin B Sin C b a A c B (3) C Exercise: Find lengths y using sine rule b 8.9cm (2) C (1) C b 34 4.2cm 41 36 62 B y cm y c a 15 22 B A y c 6cm c Y = 5.9 cm y 6 4.2 y = = Sin 15 Sin 34 Sin 22 Sin 41 6 4.2 y = x Sin 15 x Sin 41 = y Sin 34 Sin 22 y = 2.8 cm (1dp) 7.4 cm (1dp) = y
- 25. Sine Rule C b C 2.3cm 43 b a x 3.5cm B A B c c Sin B Sin C Use this when finding a length = b c a b c Sin 43 = = Sin x sin A sin B sin C = 2.3 3.5 Sin 43 or Sin x = x 2.3 3.5 Use this when finding an angle sin A sin B sin C Sin x = 0.44817….. = = x = 0.44817…..sin-1 a b c x = 26.6 (1dp)
- 26. Exercise: Find angley using sin rule Sine Rule C (2) C (1) 63 y C 2.9 cm 7.3 cm b a b a y 53 A B A c B 4.3cm c 8.4cm c Sin A = Sin B = Sin C Sin A = Sin C Sin B = Sin Y a b c a c b c Sin y Sin 63 Sin 53 Sin y = = 2.9 4.3 7.3 8.4 Sin 63 Sin 53 Sin y = x 2.9 x 8.4 = Sin y 4.3 7.3 Sin y = 0.600911….. 0.9080… Sin y = y = 0.600911….. -1 sin 0.9080… sin-1 = y y = 36.9 (1dp) 65.2 (1dp) = y
- 30. Sine Rule Practice HigherGCSE for AQA (Oxford) Book Page 387 Exercise 4r Q1 – Q19
- 31. Wednesday 8 August2012 Cosine Rule Outcomes Objective Use cosine rule to find angles and lengths in Must: Use cosine rule to find triangles. (not right lengths in triangles. angles triangles) Should: Use cosine rule to find angles in triangles. Could: Answer mixed questions
- 32. The cosine rule Use when finding a length a2 = b2 + c2 – 2bc cos A of a side. A or c b Use when cos A = b2 + c2 – a2 finding an B C 2bc Angle. a When you are given two lengths and an angle Example 1 between them use; Find a B a2 = b2 + c2 – 2bc cos A a 4 cm a2 = 72 + 42 - 2 x 7 x 4 cos 48 a2 = 27.52868….. C 48° A a = 5.25 (2dp) 7 cm
- 33. When you aregiven two lengths and an angle Example 1 between them use; Find a B a2 = b2 + c2 – 2bc cos A a 4 cm a2 = 72 + 42 - 2 x 7 x 4 cos 48 a2 = 27.52868….. C 48° A a = 5.25 (2dp) 7 cm Exercise Find the length marked x (1) (2) 2cm x 9cm 52 98 x 5cm 5cm a2 = 52 + 92 - 2 x 5 x 9 cos 98 a2 = 52 + 22 - 2 x 5 x 2 cos 52 a2 = 118.52557….. a2 = 16.68677….. a = 10.89 (2dp) a = 4.08 (2dp)
- 34. The cosine rule Use when finding a length a2 = b2 + c2 – 2bc cos A of a side. A (given 2 lengths or and an angle) c b cos A = b2 + c2 – a2 Use when B C 2bc finding an a Angle. (given 3 lengths) Example 1 You are given 3 sides and asked for an angle. Find angle A B cos A = b + c - a 2 2 2 a 2bc 8 cm c 6 cm cos A = 4 + 6 - 8 2 2 2 2x4x6 C 4 cm A cos A = - 0.25 b A = - 0.25 cos-1 A = 104. 5 (1dp)
- 35. Example 1 You are given 3 sides and asked for an angle. Find angle A cos A = b + c - a 2 2 2 B 2bc a 8 cm c cos A = 4 + 6 - 8 2 2 2 6 cm 2x4x6 A= 104. 5 (1dp) C A cos A = - 0.25 b 4 cm A = - 0.25 cos-1 Exercise Find the length marked x (2) a 11cm b (1) b 9cm 2cm x A x a A 4cm c 5cm c 5cm cos A = 9 + 5 - 11 2 2 2 2x9x5 cos A = 2 + 5 - 4 2 2 2 2x2x5 cos A = - 0.1666…. cos A = 0.65 A = - 0.166..cos-1 A = 99. 6 (1dp) A = 0.65 cos-1 A = 49.5 (1dp)
Editor's Notes
- #3 Review the definition of a right-angled triangle. Tell pupils that in any triangle the angle opposite the longest side will always be the largest angle and vice-versa. Ask pupils to explain why no other angle in a right-angled triangle can be larger than or equal to the right angle. Ask pupils to tell you the sum of the two smaller angles in a right-angled triangle. Recall that the sum of the angles in a triangle is always equal to 180 °. Recall, also, that two angles that add up to 90° are called complementary angles. Conclude that the two smaller angles in a right-angled triangle are complementary angles.
- #4 We don ’t don’t need to know the actual size of the marked angle to label the two shorter sides as shown. It could be labelled using a letter symbol such as x as shown here. Point out that if we labelled the sides with respect to the other acute angle their name would be reversed.
- #5 Use this activity to practice labelling the sides of a right-angled triangle with respect to angle θ . Ask volunteers to come to the board to complete the activity.
- #6 This exercise practices the use of the sin, cos and tan keys on the calculator. It also practices rounding to a given number of significant figures. Pupils should notice that the sine of a given angle is equal to the cosine of the complement of that angle. They can use this fact to answer question 10 using the answer to question 5.
- #7 Stress to pupils that they must learn these three trigonometric ratios. Pupils can remember these using SOHCAHTOA or they may wish to make up their own mnemonics using these letters.
- #8 The sine ratio depends on the size of the opposite angle. We say that the sine of the angle is equal to the length of the opposite side divided by the length of the hypotenuse. Sin is mathematical shorthand for sine. It is still pronounced as ‘sine’.
- #9 This ratio can also be demonstrated using the similar right-angled activity on slide 7.
- #10 This ratio can also be demonstrated using the similar right-angled activity on slide 7.
- #11 This ratio can also be demonstrated using the similar right-angled activity on slide 7.
- #12 This ratio can also be demonstrated using the similar right-angled activity on slide 7.
- #33 We can use the first form of the formula to find side lengths and the second form of the equation to find angles.
- #35 We can use the first form of the formula to find side lengths and the second form of the equation to find angles.