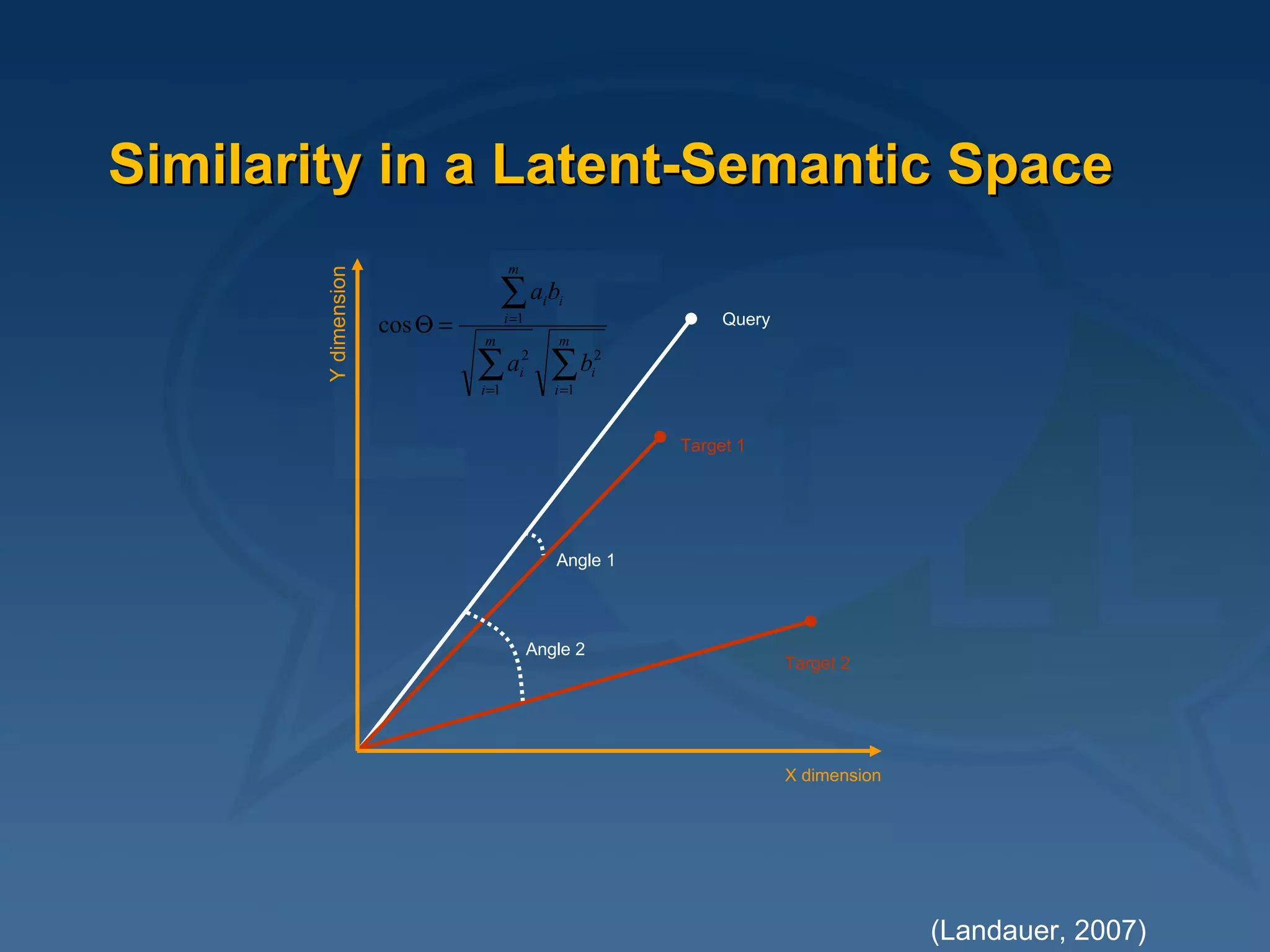
This document provides an overview of using latent semantic analysis (LSA) and the R programming language for language technology enhanced learning applications. It describes using LSA to create a semantic space to compare documents and evaluate student writings. It also demonstrates clustering terms based on their semantic similarity and visualizing networks in R. Evaluation results show LSA machine scores for essay quality had a Spearman's rank correlation of 0.687 with human scores, outperforming a pure vector space model.

1. Language Technology Enhanced Learning Fridolin Wild The Open University, UK Gaston Burek University of Tübingen Adriana Berlanga Open University, NL

2. Workshop Outline 1 | Deep Introduction Latent-Semantic Analysis (LSA) 2 | Quick Introduction Working with R 3 | Experiment Simple Content-Based Feedback 4 | Experiment Topic Proxy #

3. Latent-Semantic Analysis LSA

4. Latent Semantic Analysis Assumption: language utterances do have a semantic structure However, this structure is obscured by word usage (noise, synonymy, polysemy, …) Proposed LSA Solution: map doc-term matrix using conceptual indices derived statistically (truncated SVD ) and make similarity comparisons using e.g. angles

5. Input (e.g., documents) { M } = Deerwester, Dumais, Furnas, Landauer, and Harshman (1990): Indexing by Latent Semantic Analysis, In: Journal of the American Society for Information Science, 41(6):391-407 Only the red terms appear in more than one document, so strip the rest. term = feature vocabulary = ordered set of features TEXTMATRIX

6. Singular Value Decomposition =

7. Truncated SVD … we will get a different matrix (different values, but still of the same format as M). latent-semantic space

8. Reconstructed, Reduced Matrix m4: Graph minors : A survey

9. Similarity in a Latent-Semantic Space (Landauer, 2007) Query Target 1 Target 2 Angle 2 Angle 1 Y dimension X dimension

10. doc2doc - similarities Unreduced = pure vector space model - Based on M = TSD’ - Pearson Correlation over document vectors reduced - based on M 2 = TS 2 D’ - Pearson Correlation over document vectors

11. (Landauer, 2007)

12. Configurations 4 x 12 x 7 x 2 x 3 = 2016 Combinations

13. Updating: Folding-In SVD factor stability Different texts – different factors Challenge: avoid unwanted factor changes (e.g., bad essays) Solution: folding-in instead of recalculating SVD is computationally expensive 14 seconds (300 docs textbase) 10 minutes (3500 docs textbase) … and rising!

14. The Statistical Language and Environment R R

16. Help > ?'+' > ?kmeans > help.search("correlation") http://www.r-project.org => site search => documentation Mailinglist r-help Task View NLP: http://cran.r-project.org/ -> Task Views -> NLP

17. Installation & Configuration install.packages("lsa", repos="http://cran.r-project.org") install.packages("tm", repos="http://cran.r-project.org") install.packages("network", repos="http://cran.r-project.org") library(lsa) setwd("d:/denkhalde/workshop") dir() ls() quit()

18. The lsa Package Available via CRAN, e.g.: http://cran.at.r-project.org/src/contrib/Descriptions/lsa.html Higher-level Abstraction to Ease Use Five core methods: textmatrix() / query() lsa() fold_in() as.textmatrix() Supporting methods for term weighting, dimensionality calculation, correlation measurement, triple binding

19. Core Processing Workflow tm = textmatrix(‘dir/‘) tm = lw_logtf(tm) * gw_idf(tm) space = lsa(tm, dims=dimcalc_share()) tm3 = fold_in(tm, space) as.textmatrix(tm)

20. A Simple Evaluation of Students Writings Feedback

21. Evaluating Student Writings External Validation? Compare to Human Judgements! (Landauer, 2007)

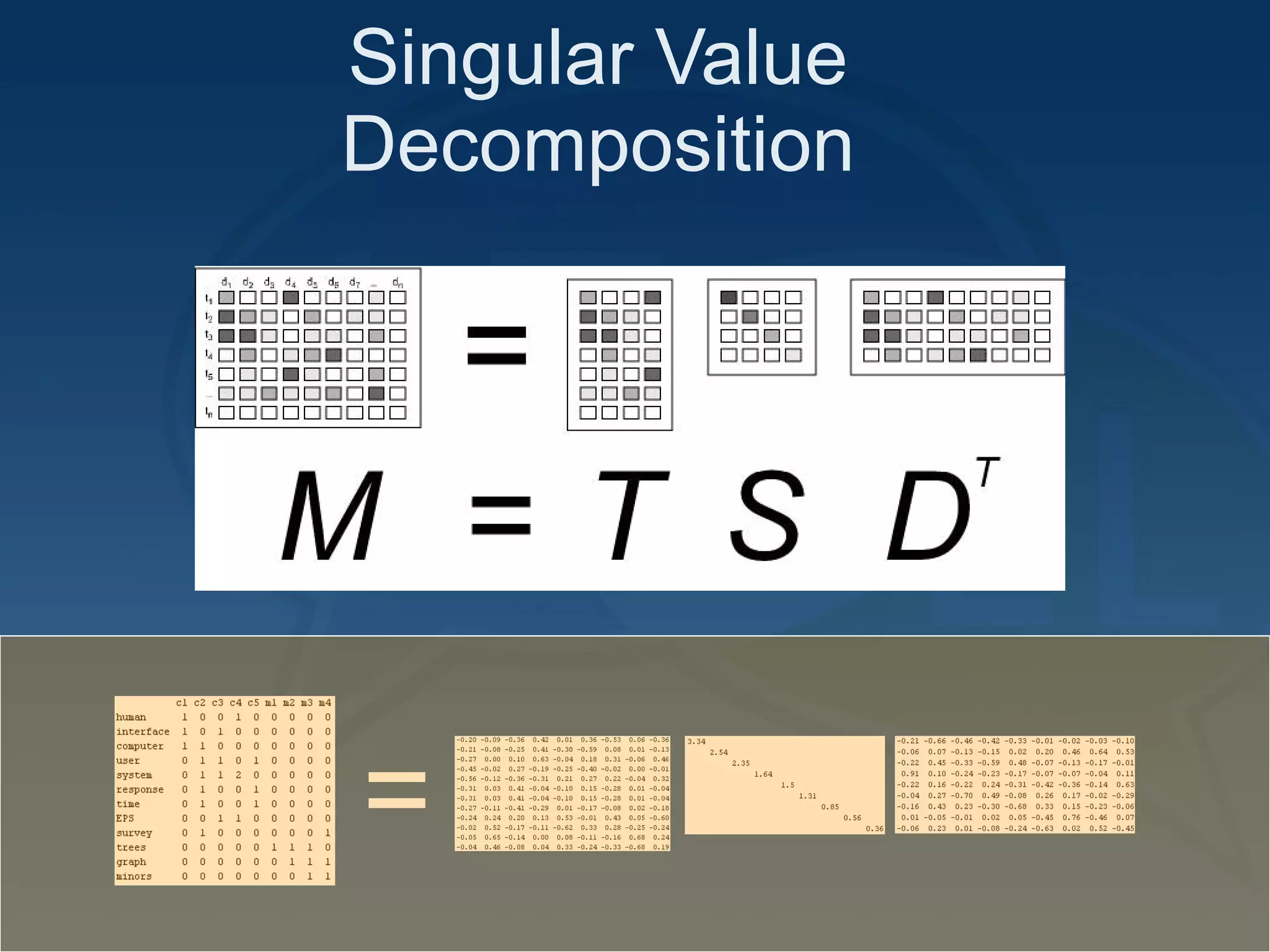
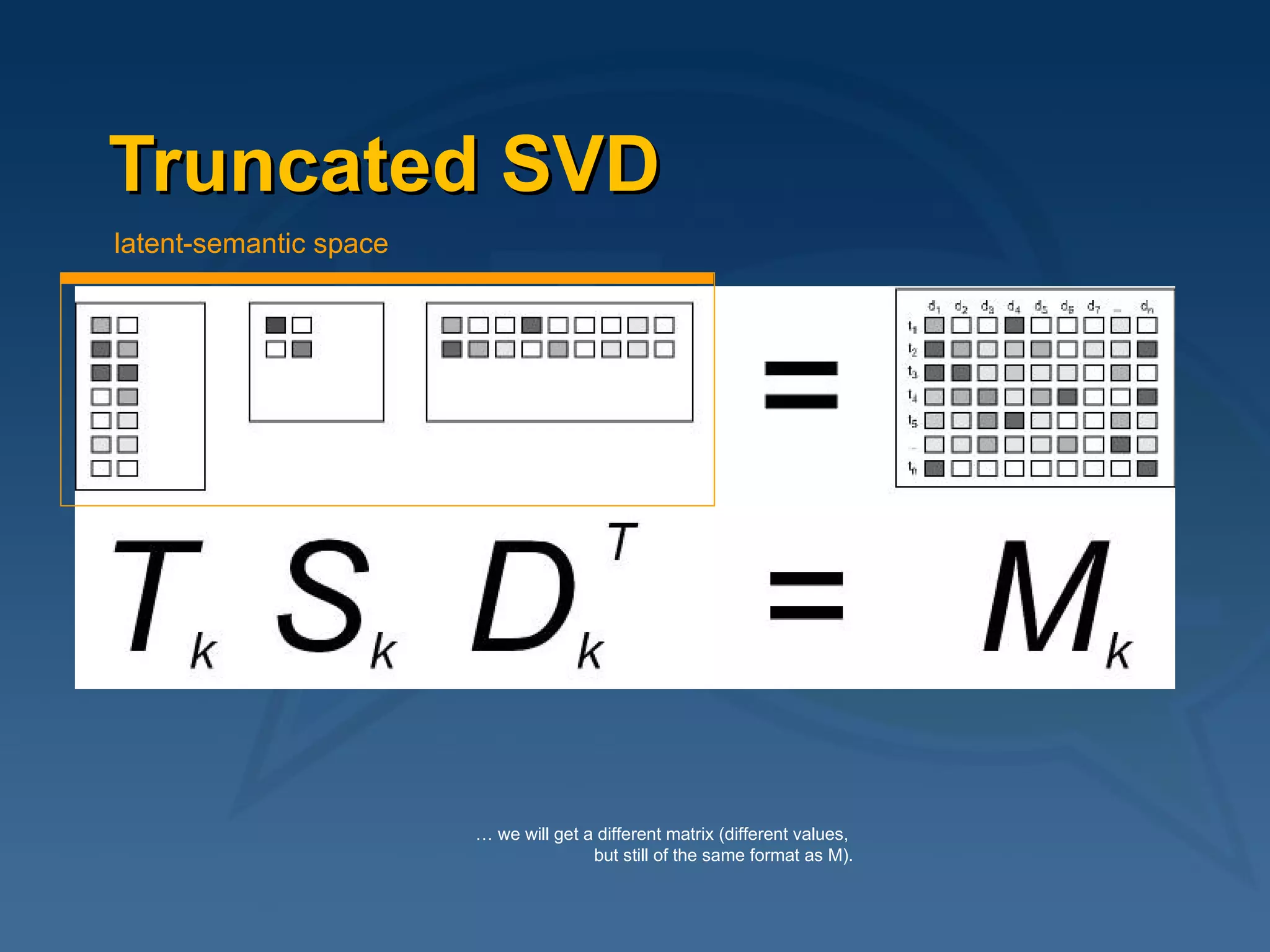
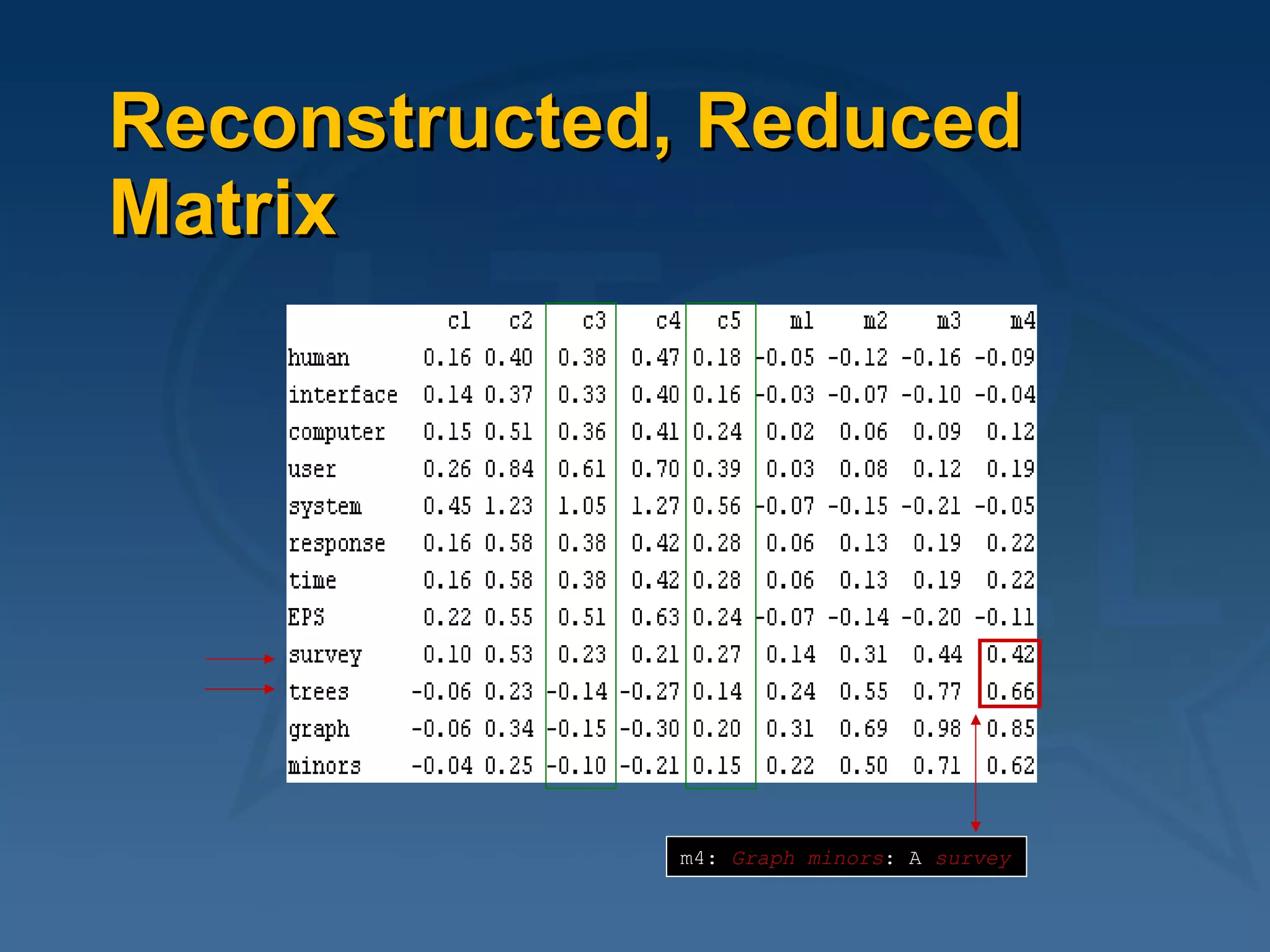
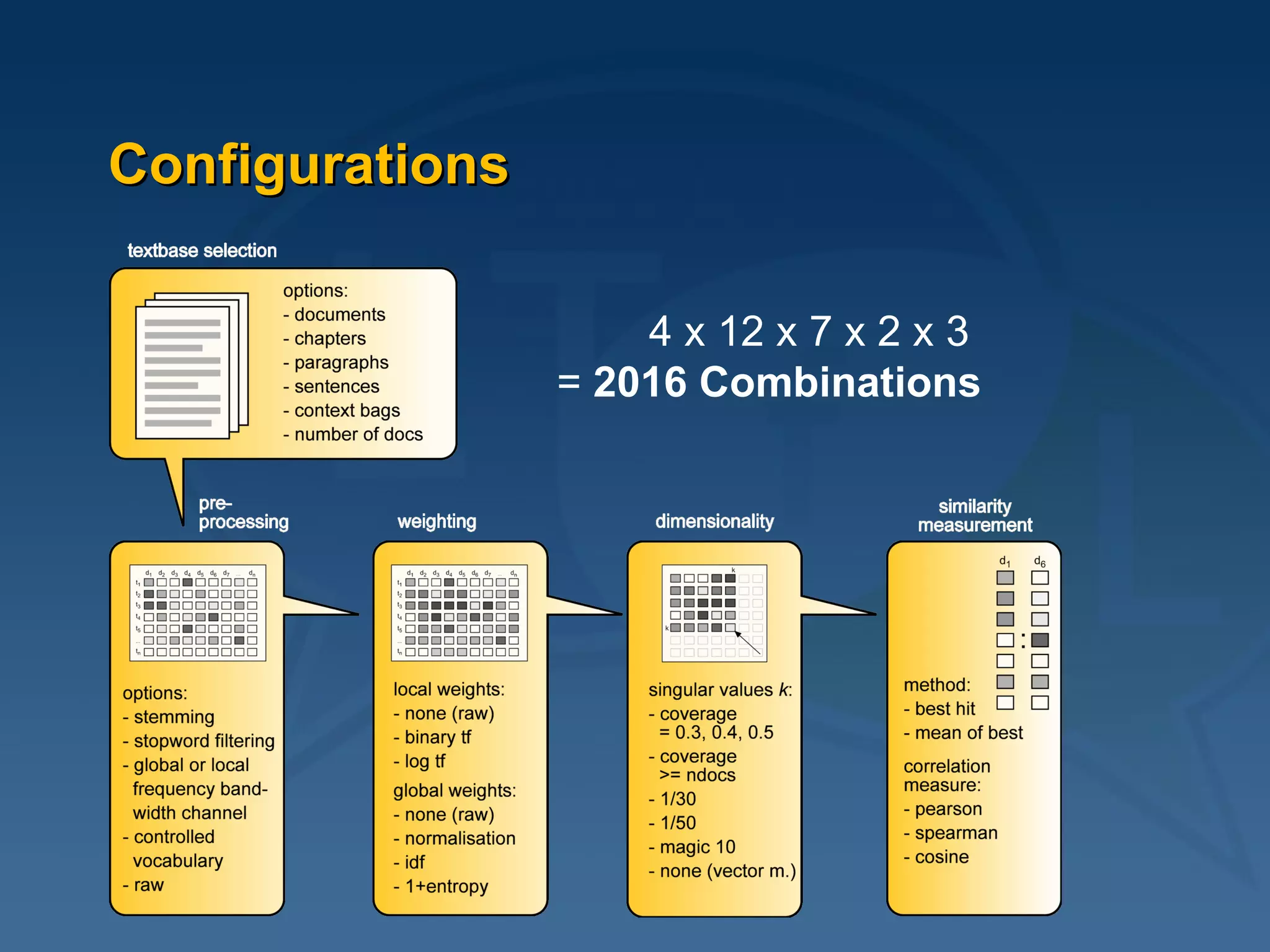
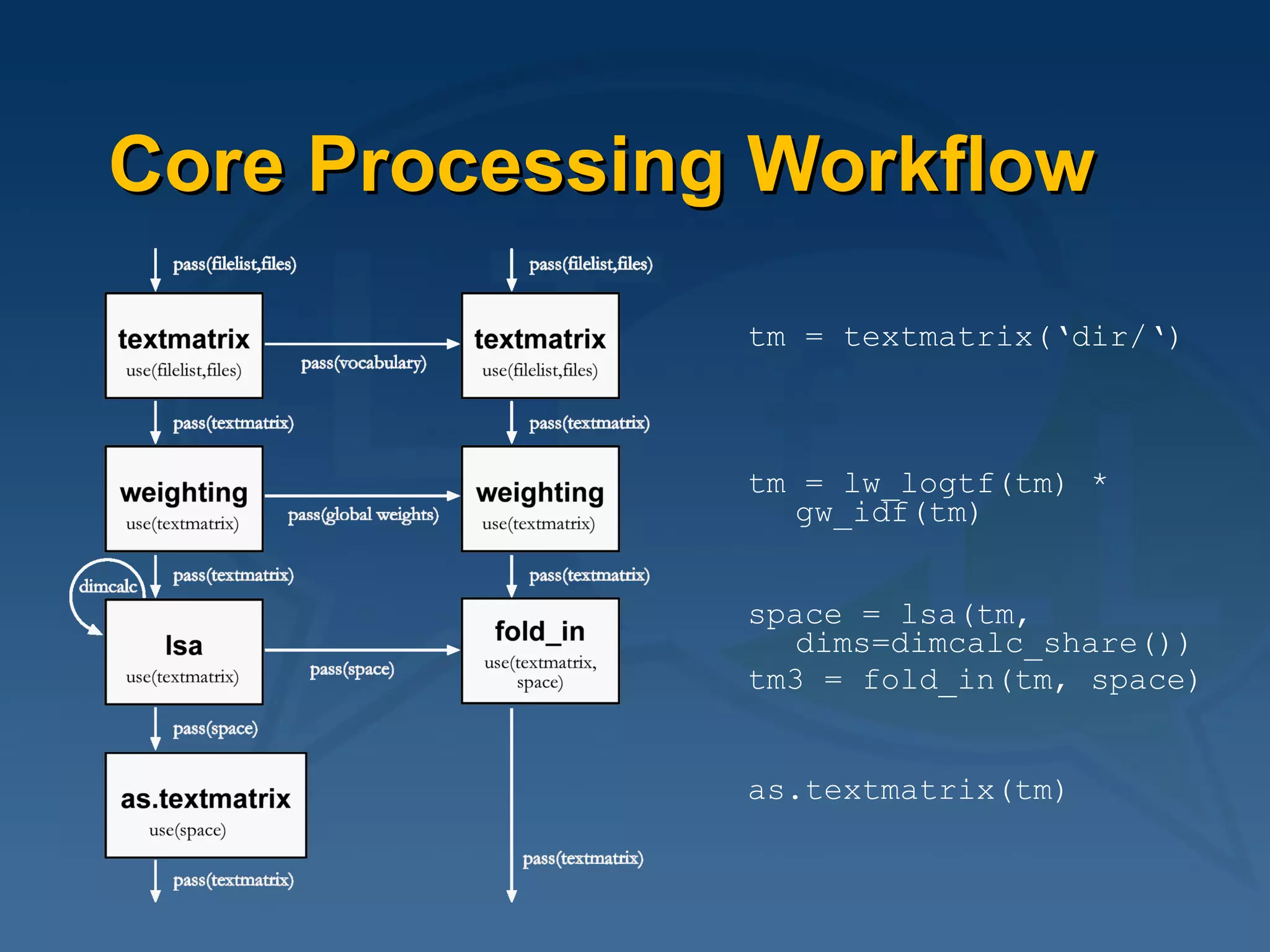
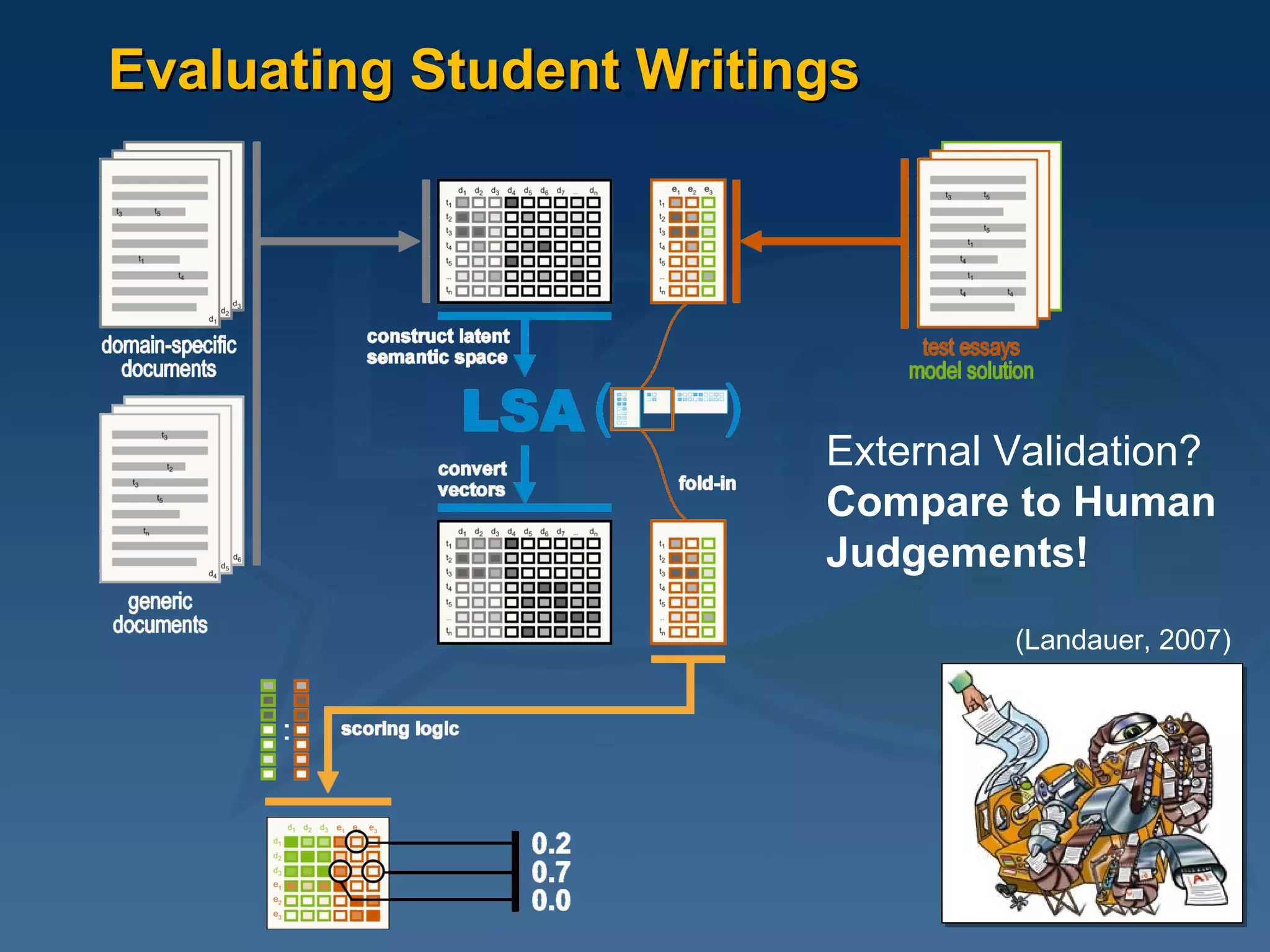
22. How to do it... library( "lsa“ ) # load package # load training texts trm = textmatrix( "trainingtexts/“ ) trm = lw_bintf( trm ) * gw_idf( trm ) # weighting space = lsa( trm ) # create an LSA space # fold-in essays to be tested (including gold standard text) tem = textmatrix( "testessays/", vocabulary=rownames(trm) ) tem = lw_bintf( tem ) * gw_idf( trm ) # weighting tem_red = fold_in( tem, space ) # score an essay by comparing with # gold standard text (very simple method!) cor( tem_red[,"goldstandard.txt"], tem_red[,"E1.txt"] ) => 0.7

23. Evaluating Effectiveness Compare Machine Scores with Human Scores Human-to-Human Correlation Usually around .6 Increased by familiarity between assessors, tighter assessment schemes, … Scores vary even stronger with decreasing subject familiarity (.8 at high familiarity, worst test -.07) Test Collection: 43 German Essays, scored from 0 to 5 points (ratio scaled), average length: 56.4 words Training Collection: 3 ‘golden essays’, plus 302 documents from a marketing glossary, average length: 56.1 words

24. (Positive) Evaluation Results LSA machine scores: Spearman's rank correlation rho data: humanscores[names(machinescores), ] and machinescores S = 914.5772, p-value = 0.0001049 alternative hypothesis: true rho is not equal to 0 sample estimates: rho 0.687324 Pure vector space model: Spearman's rank correlation rho data: humanscores[names(machinescores), ] and machinescores S = 1616.007, p-value = 0.02188 alternative hypothesis: true rho is not equal to 0 sample estimates: rho 0.4475188

25. Concept-Focused Evaluation (using http://eczemablog.blogspot.com/feeds/posts/default?alt=rss)

26. Visualising Lexical Semantics Topic Proxy

27. Network Visualisation Term-2-Term distance matrix = = Graph t 1 t 2 t 3 t 4 t 1 1 t 2 -0.2 1 t 3 0.5 0.7 1 t 4 0.05 -0.5 0.3 1

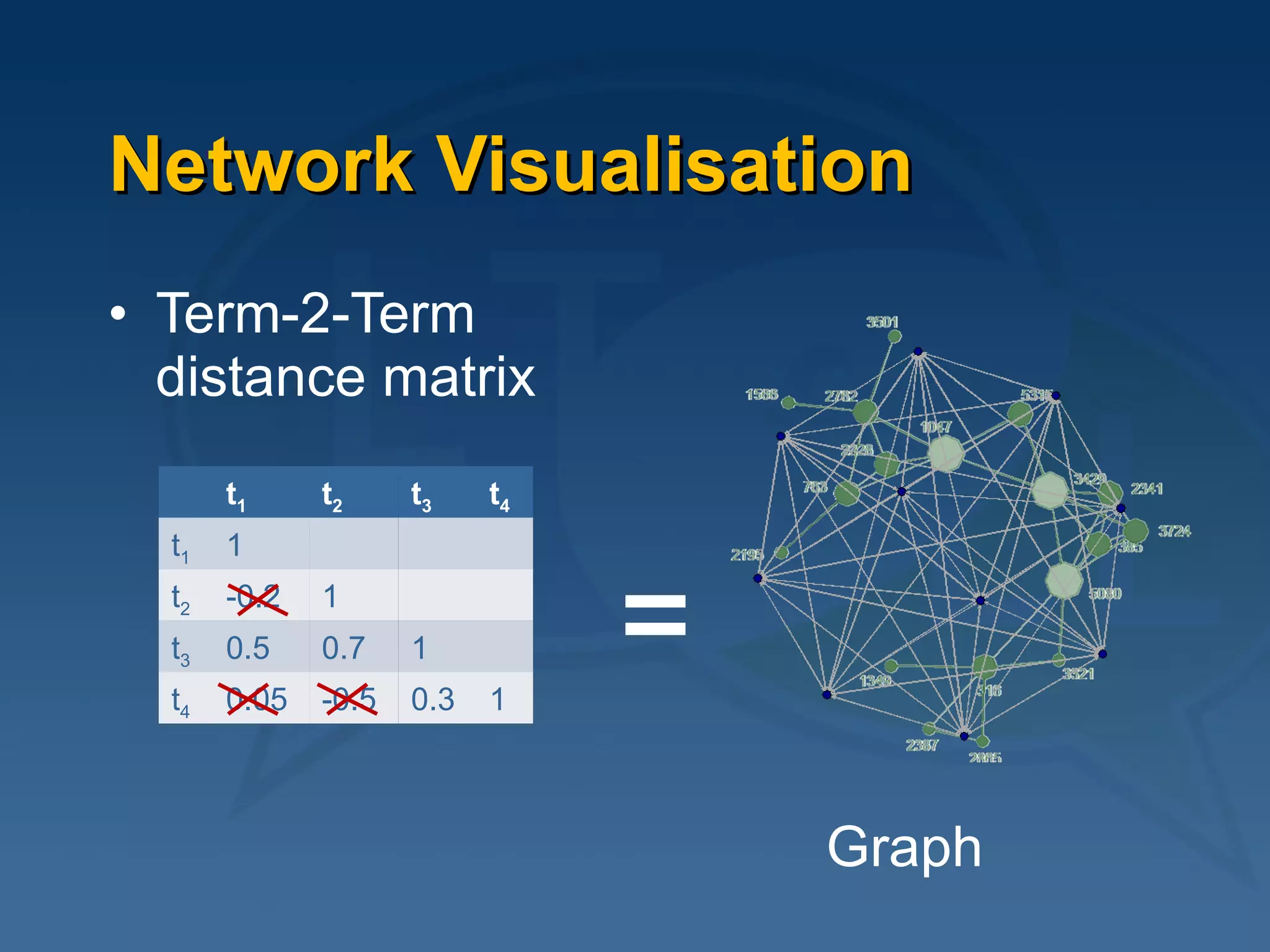
28. Classical Landauer Example tl = landauerSpace$tk %*% diag(landauerSpace$sk) dl = landauerSpace$dk %*% diag(landauerSpace$sk) dtl = rbind(tl,dl) s = cosine(t(dtl)) s[which(s<0.8)] = 0 plot( network(s), displaylabels=T, vertex.col = c(rep(2,12), rep(3,9)) )

29. Divisive Clustering (Diana)

30. edmedia Terminology

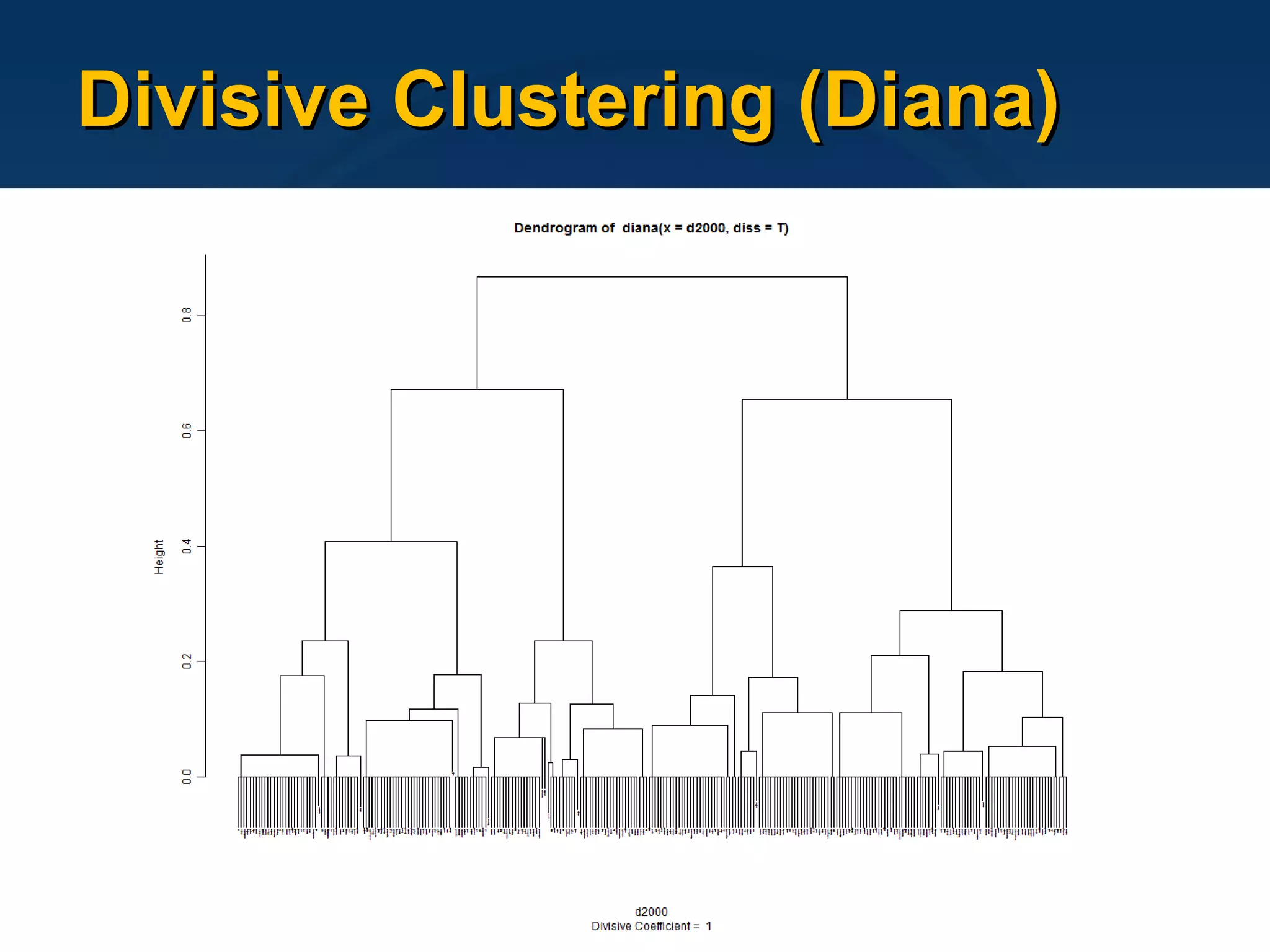
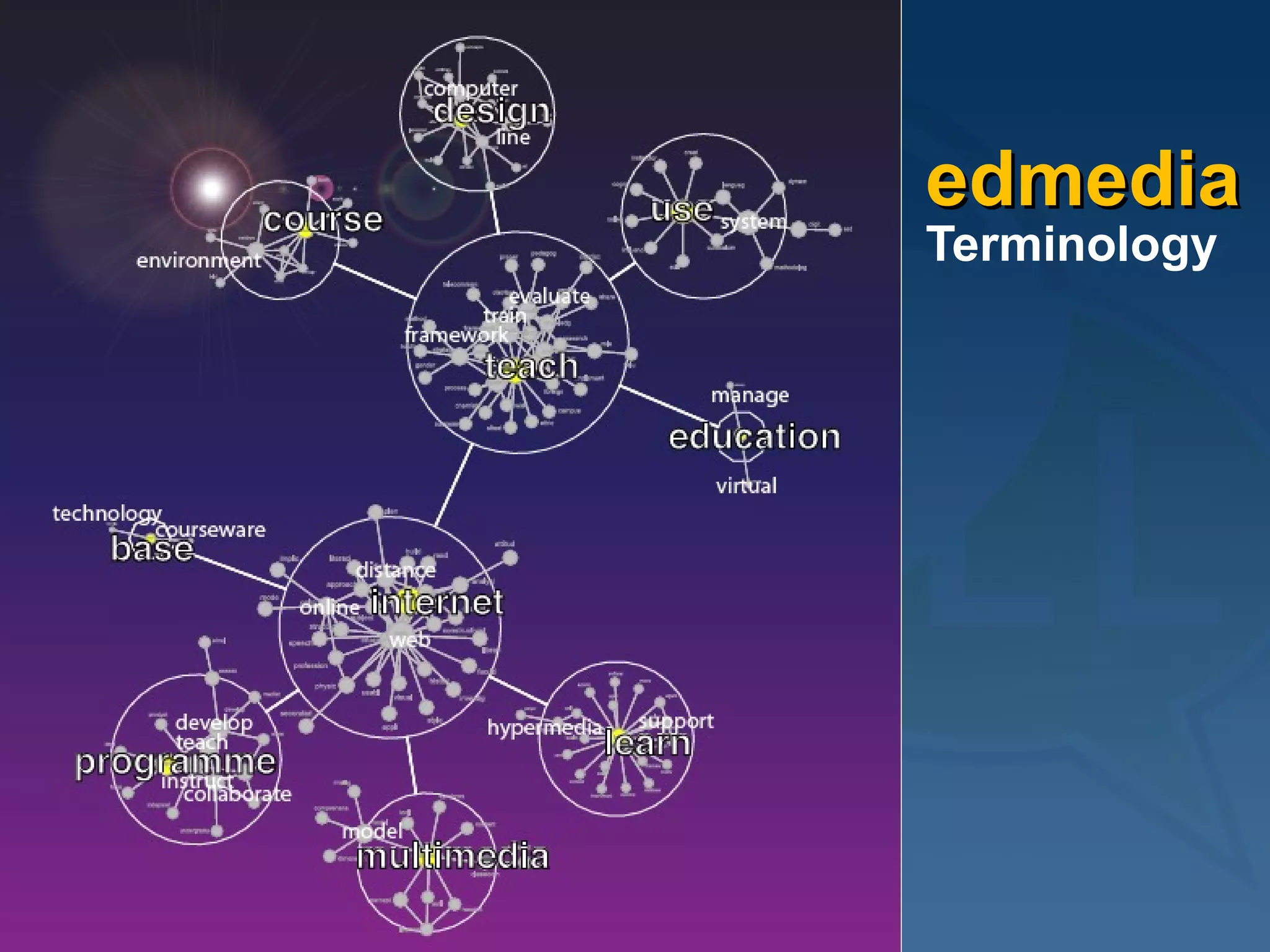
31. Code Sample d2000 = cosine(t(dtm2000)) dianac2000 = diana(d2000, diss=T) clustersc2000 = cutree(as.hclust(dianac2000), h=0.2) plot(dianac2000, which.plot=2, cex=.1) # dendrogramme winc = clustersc2000[which(clustersc2000==1)] # filter for cluster 1 wincn = names(winc) d = d2000[wincn,wincn] d[which(d<0)] == 0 btw = betweenness(d, cmode=&quot;undirected&quot;) # for nodes size calc btwmax = colnames(d)[which(btw==max(btw))] btwcex = (btw/max(btw))+1 plot(network(d), displayisolates=F, displaylabels=T, boxed.labels=F, edge.col=&quot;gray&quot;, main=paste(&quot;cluster&quot;,i), usearrows=F, vertex.border=&quot;darkgray&quot;, label.col=&quot;darkgray&quot;, vertex.cex=btwcex*3, vertex.col=8-(colnames(d) %in% btwmax))

32. Permutating Permutation

33. Permutation test NON PARAMETRIC: does not assume that the data have a particular probability distribution . Suppose the following ranking of elements of two categories X and Y Actual data to be evaluated, (x_1,x_2,y_1) = (1,9,2). Let, T(x_1,x_2,y_1)=abs(mean X- mean Y) = 2

34. Permutation Usually, it is not practical to evaluate all N! permutatioons. We can approximate the p-value by sampling randomly from the set of permutations.

35. The permutations are: permutation value of T -------------------------------------------- (1,9,3) 2 (actual data) (9,1,3) 2 (1,3,9) 7 (3,1,9) 7 (3,9,1) 5 (9,3,1) 5

36. Some results Students discussions on safe prescribing: Classified according expected learning outcomes related subtopics topics: A=7, B=12, C=53, D=4, E=40, F=7 Graded: poor, fair, good, excelent Methodology used: LSA Bag of words/Maximal Repeated Phrases Permutation test

37. Challenging Questions Discussion

38. Questions Dangers of using Language Technology? Ontologies = Neat? NLP = Nasty? Other possible application areas? Corpus Collection? What is good effectiveness? When can we say that an algorithm works well? Other aspects not evaluated…

39. Questions? #eof.