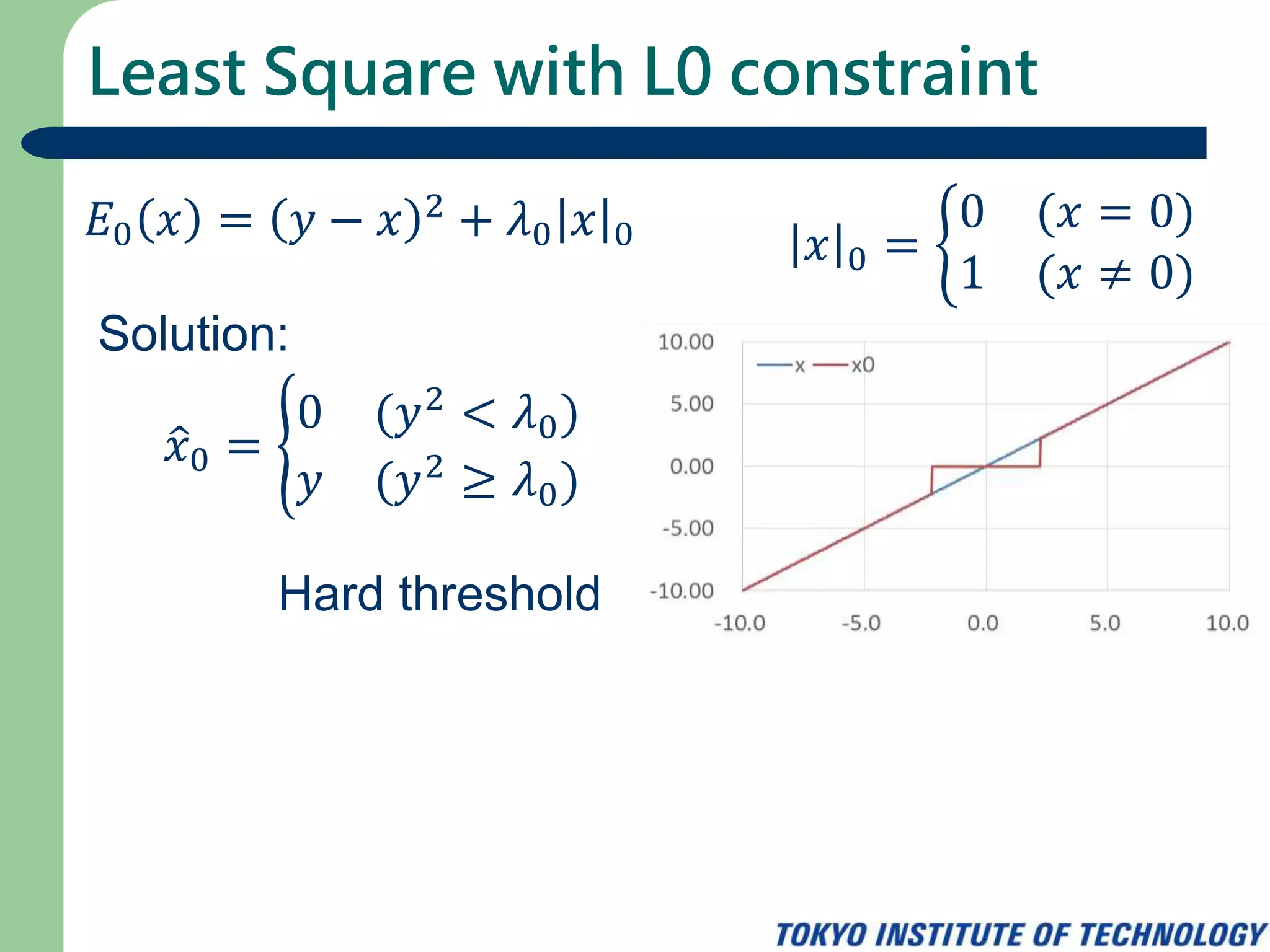
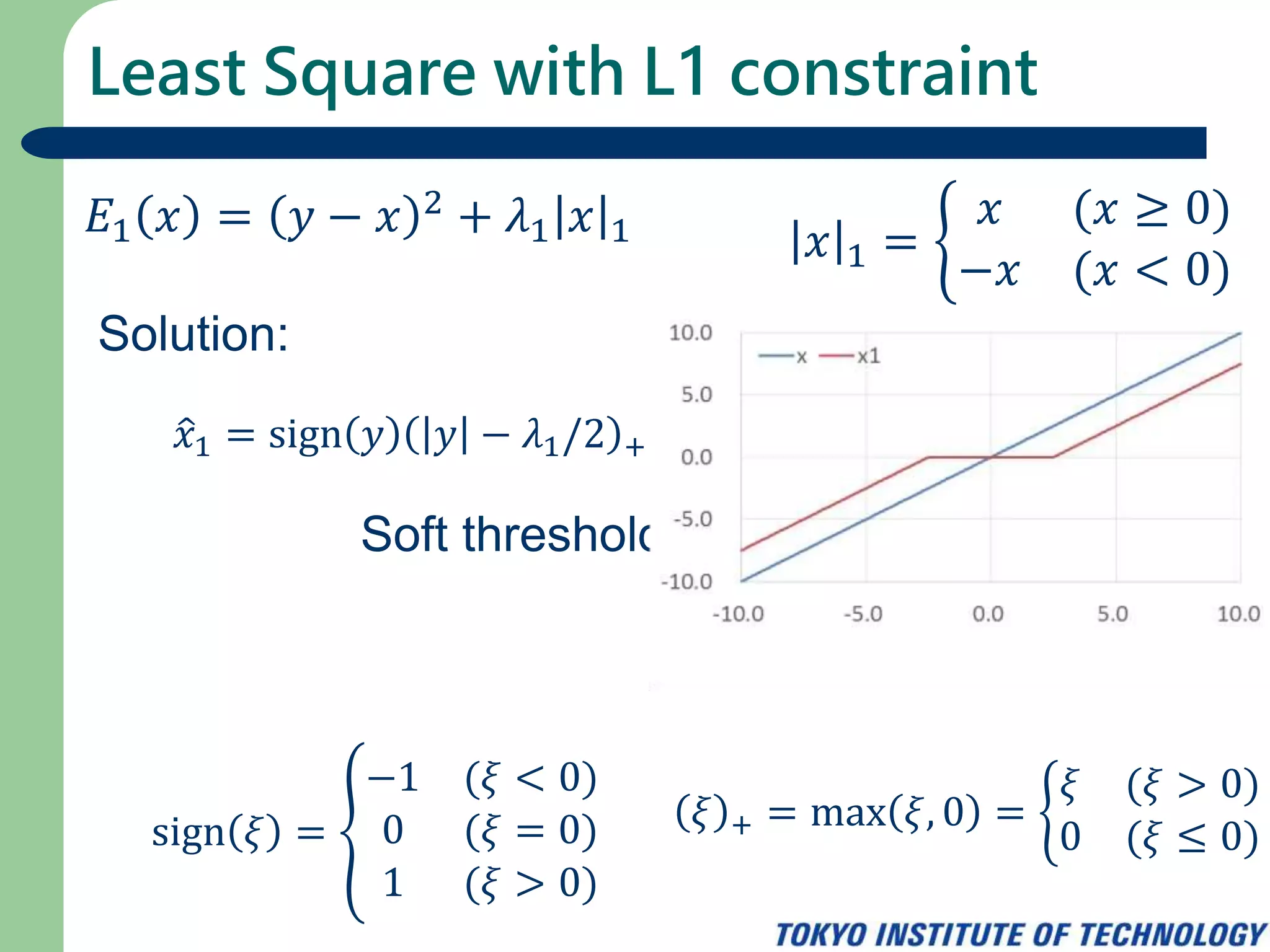
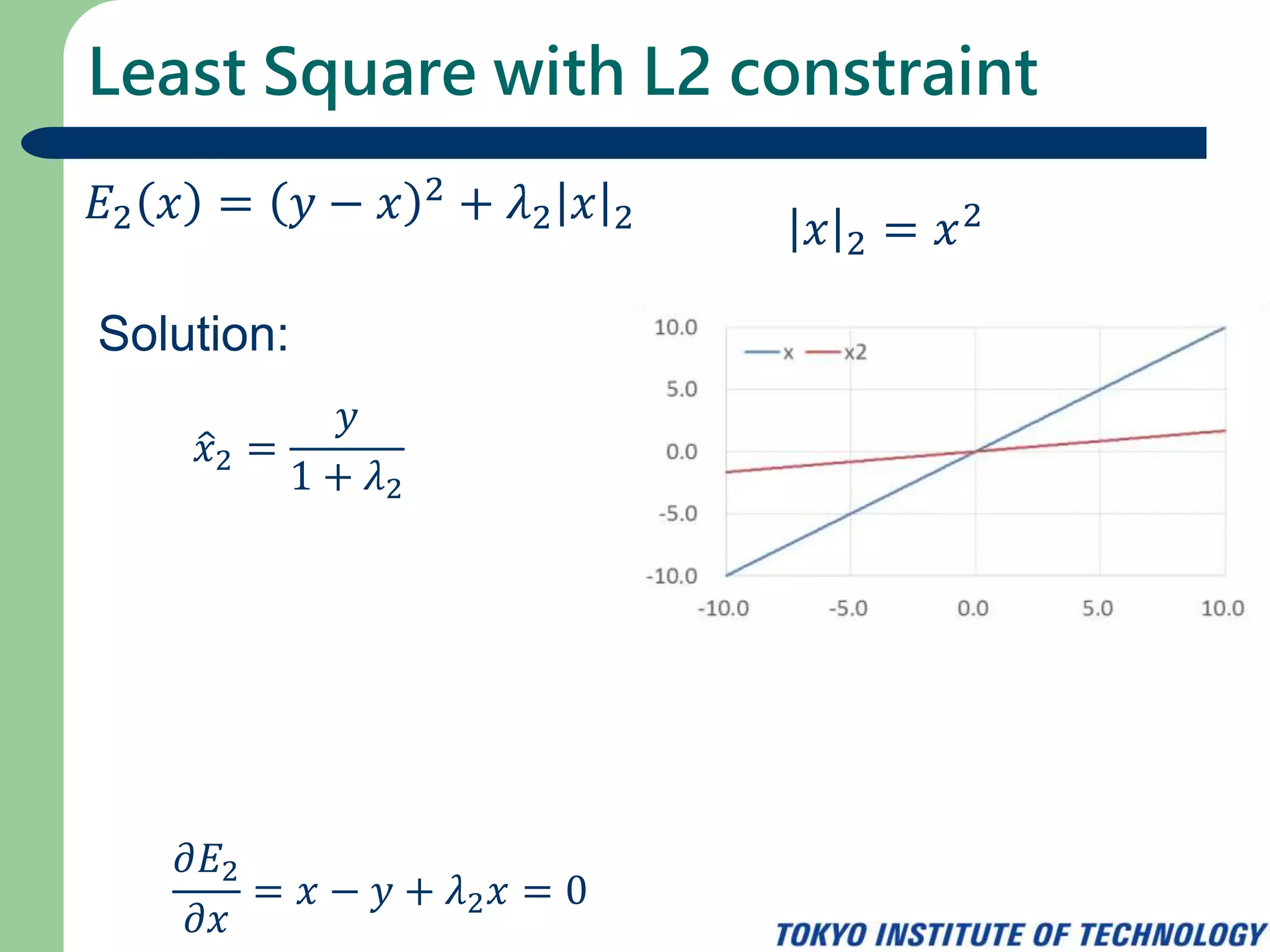
The document discusses least square regression with L0, L1, and L2 constraints. It presents the cost functions for each constraint and derives the solutions. For L0 constraint, the solution is a hard threshold determined by comparing the squared value to the regularization parameter. For L1 constraint, the solution is a soft threshold. For L2 constraint, the solution is obtained by setting the derivative of the cost function to zero. It also formulates L0 and L1 constraints as proximal operators.

1. Masayuki Tanaka
Jun. 22, 2016
Least Square with
L0, L1, and L2 Constraint

2. Cost Functions
𝐸2 𝑥 = 𝑦 − 𝑥 2 + 𝜆2 𝑥 2 𝑥 2 = 𝑥2
𝐸1 𝑥 = 𝑦 − 𝑥 2 + 𝜆1 𝑥 1 𝑥 1 =
𝑥 (𝑥 ≥ 0)
−𝑥 (𝑥 < 0)
𝐸0 𝑥 = 𝑦 − 𝑥 2 + 𝜆0 𝑥 0 𝑥 0 =
0 (𝑥 = 0)
1 (𝑥 ≠ 0)

3. Least Square with L0 constraint
𝐸0 𝑥 = 𝑦 − 𝑥 2 + 𝜆0 𝑥 0 𝑥 0 =
0 (𝑥 = 0)
1 (𝑥 ≠ 0)
𝑥0 =
0 (𝑦2 < 𝜆0)
𝑦 (𝑦2
≥ 𝜆0)
Hard threshold
Solution:

4. Least Square with L1 constraint
𝑥1 = sign 𝑦 𝑦 − 𝜆1/2 +
sign 𝜉 =
−1 (𝜉 < 0)
0 (𝜉 = 0)
1 (𝜉 > 0)
𝜉 + = max 𝜉, 0 =
𝜉 (𝜉 > 0)
0 (𝜉 ≤ 0)
Soft threshold
𝐸1 𝑥 = 𝑦 − 𝑥 2 + 𝜆1 𝑥 1 𝑥 1 =
𝑥 (𝑥 ≥ 0)
−𝑥 (𝑥 < 0)
Solution:

5. Least Square with L2 constraint
𝜕𝐸2
𝜕𝑥
= 𝑥 − 𝑦 + 𝜆2 𝑥 = 0
𝑥2 =
𝑦
1 + 𝜆2
𝐸2 𝑥 = 𝑦 − 𝑥 2
+ 𝜆2 𝑥 2 𝑥 2 = 𝑥2
Solution:

6. Derivation of
Least Square with L0 constraint
𝐸0 𝑥 = 𝑦 − 𝑥 2 + 𝜆0 𝑥 0 𝑥 0 =
0 (𝑥 = 0)
1 (𝑥 ≠ 0)
𝑥 = 0 𝑥 ≠ 0
𝐸0 0 = y2 𝐸0 𝑥 = 𝑦 − 𝑥 2 + 𝜆0 min
𝑥≠0
𝐸0 𝑥 = 𝜆0
𝑦
𝜆0− 𝜆0
𝑥0 = 0
𝐸0 𝑥0 = 𝑦2
𝑥0 = 𝑦
𝐸0 𝑥0 = 𝜆0
𝑥0 = 𝑦
𝐸0 𝑥0 = 𝜆0
𝑥0 =
0 (𝑦2 < 𝜆0)
𝑦 (𝑦2
≥ 𝜆0)
Hard threshold

7. Formulation as a Proximal Operator
prox 𝐿0,𝜌 𝑦 = arg min
𝑥
𝑥 0 +
𝜌
2
𝑦 − 𝑥 2 𝑥 0 =
0 (𝑥 = 0)
1 (𝑥 ≠ 0)
=
0, 𝑦2
<
2
𝜌
1, 𝑦2 ≥
2
𝜌

8. Formulation as a Proximal Operator
prox 𝐿1,𝜌 𝑦 = arg min
𝑥
𝑥 1 +
𝜌
2
𝑦 − 𝑥 2 𝑥 1 =
𝑥 (𝑥 ≥ 0)
−𝑥 (𝑥 < 0)
= sign 𝑦 𝑦 − 1/𝜌 +
sign 𝜉 =
−1 (𝜉 < 0)
0 (𝜉 = 0)
1 (𝜉 > 0)
𝜉 + = max 𝜉, 0 =
𝜉 (𝜉 > 0)
0 (𝜉 ≤ 0)