1. 2013/02/06
卒業研究発表
実対称帯行列向け分割統治法の拡張
今村研究室
B4 0811112 山中 将一

2. 発表の流れ
● 研究内容
● 研究成果
– 分割統治法(D&C)アルゴリズム
– ELPA概要
– ELPA改良点調査
– ELPA通信体系調査
– ＥＬＰＡ と ScaLAPACK 比較実験
● まとめ
● 今後の課題
2

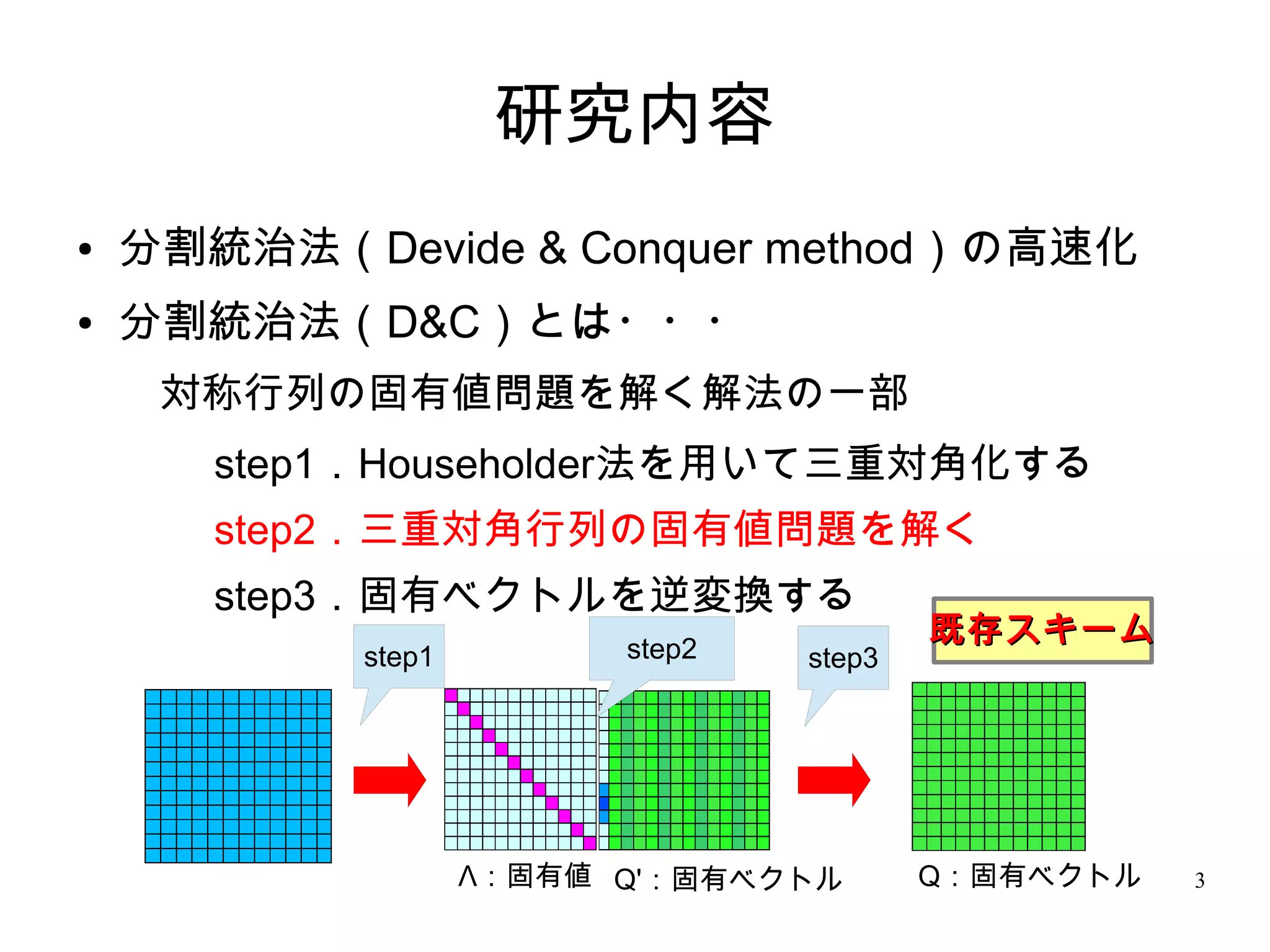
3. 研究内容
● 分割統治法（Devide & Conquer method）の高速化
● 分割統治法（D&C）とは・・・
対称行列の固有値問題を解く解法の一部
step1．Householder法を用いて三重対角化する
step2．三重対角行列の固有値問題を解く
step3．固有ベクトルを逆変換する
step2
既存スキーム
step1 step3
Λ：固有値 Q'：固有ベクトル Q：固有ベクトル 3

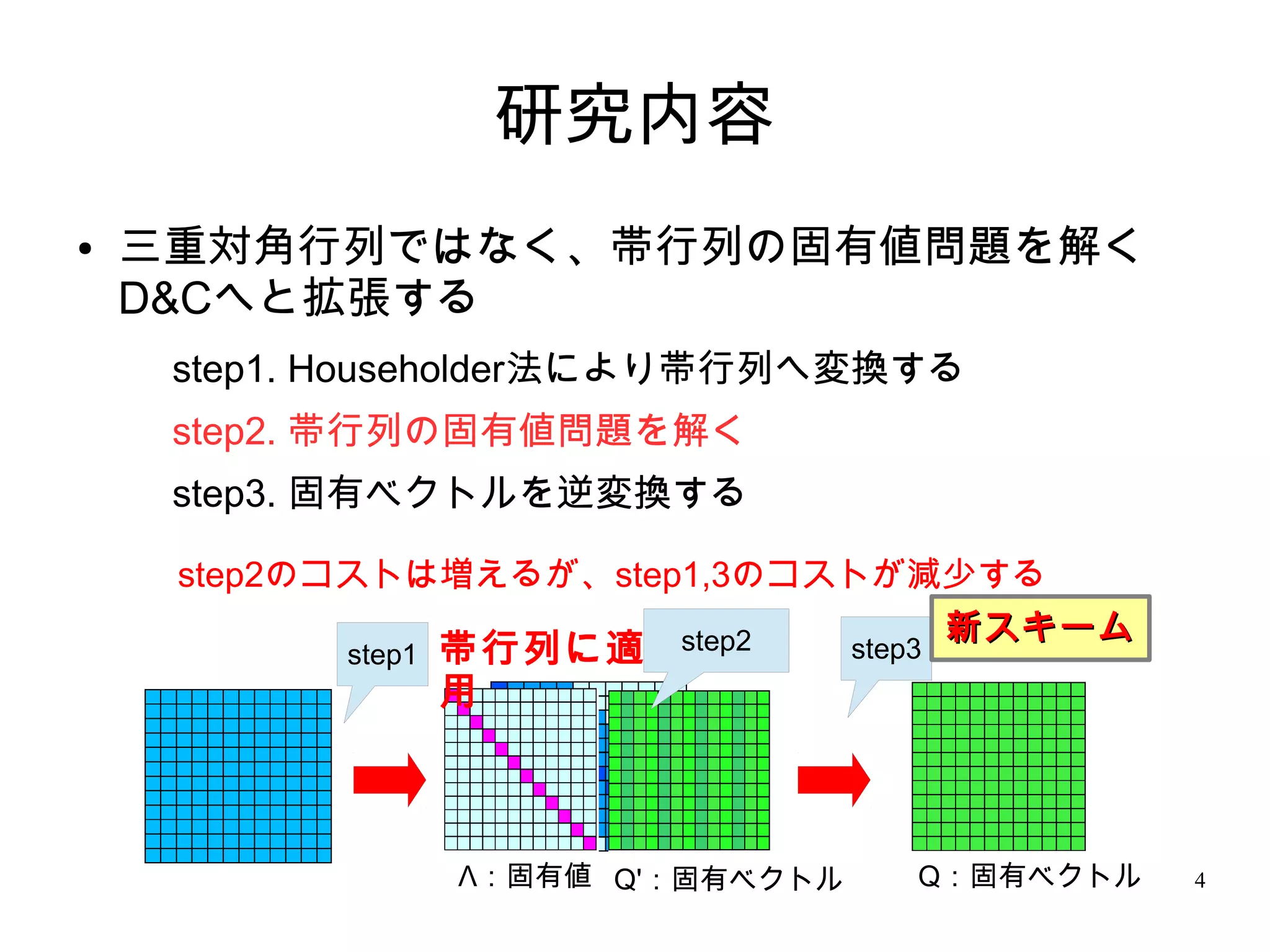
4. 研究内容
● 三重対角行列ではなく、帯行列の固有値問題を解く
D&Cへと拡張する
step1. Householder法により帯行列へ変換する
step2. 帯行列の固有値問題を解く
step3. 固有ベクトルを逆変換する
step2のコストは増えるが、step1,3のコストが減少する
新スキーム
step1 帯行列に適step2 step3
用
Λ：固有値 Q'：固有ベクトル Q：固有ベクトル 4

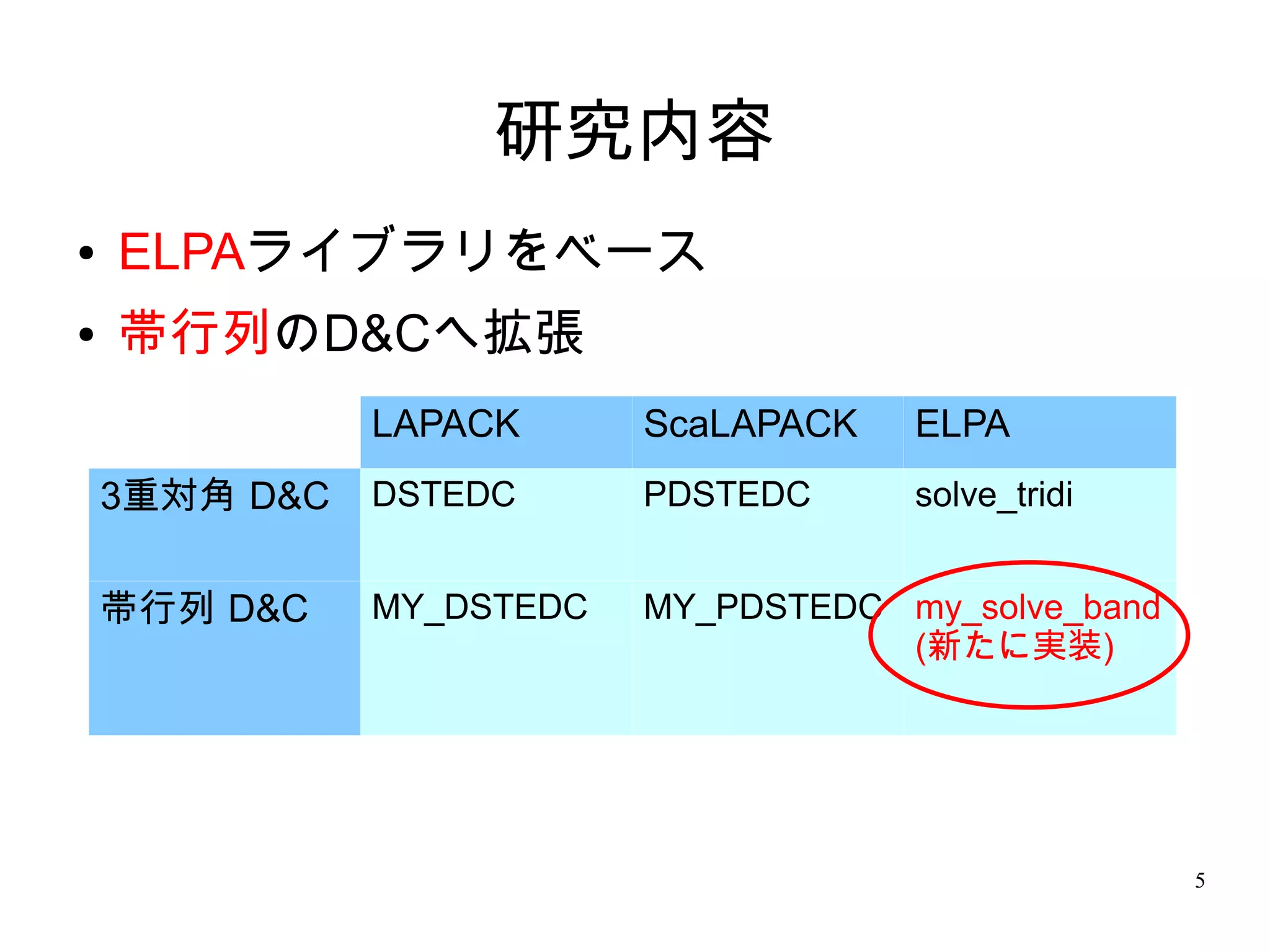
5. 研究内容
● ELPAライブラリをベース
● 帯行列のD&Cへ拡張
LAPACK ScaLAPACK ELPA
3重対角 D&C DSTEDC PDSTEDC solve_tridi
帯行列 D&C MY_DSTEDC MY_PDSTEDC my_solve_band
(新たに実装)
5

6. 3重対角D&Cアルゴリズム
3重対角向けD&Cのアルゴリズム
procedure tridiagonal eigen(T , Q , D)
(
(1)T = 1
T
) T2
+ b m vv T に分割する 分割
(2)tridiagonal eigen(T 1 , Q1 , D1 )
(3)tridiagonal eigen(T 2 , Q 2 , D 2 )
(4)Q 1 ,Q 2 , D1 , D2 で D+ cuuT を形成する
(5) deflate( D , c , u) De e作
a
lt
f 業
(6) rank1(d , c , u , Λ ,Q ' ) 1階 摂 動 cuuT =Q ' Λ Q ' T を解く
D+
統治
(
(7)Q= 1
Q
) Q2
∗Q ' を計算する
returnQ , D=Λ
6

7. 帯行列D&Cアルゴリズム
帯行列向けD&Cのアルゴリズム
procedure bandmatrix eigen(T ,Q , D) (8) for j :=1から k do
begin
統治
( )
T
T1 C
(1)T = に分解する 分割 (9) u j =Uの j番 目 の 列
C T2
if j=1then
(2) DGESVD (C ,W , S ,V ,...) (10) w j =u 1
1/2 1/2 T
(3)Q=W ×S , R=S ×V else
( )
T
T 1 −R R (11) w j =Q ' u j
+ UU の形に変換する
T
(4)T = ( j−1)
T 2 −QQ T (12) deflate ( D , c j , w j)
( j−1) ( j) ( j)
T
(5)bandmatrix eigen(T 1 −R R , Q 1 , D 1 ) (13) rank1( D ,c j , w j , D ,Q )
T
(6)bandmatrix eigen(T 2 −QQ ,Q 2 , D 2 ) if j=1then
(14) Q ' =Q (1)
(0)
(7) D =
( D1
D2 ) (15)
else
Q ' =Q '∗Q
( j)
end ;
(16)Q= 1
( Q
Q2 )
∗Q '
( j)
7
return Q , D= D

8. ELPA 概要
● Eigenvalue soLvers for Petaflops Applications
● （大規模な）対称行列の固有値問題を（並列に）解く
● BLAS、LAPACK、BLACS、ScaLAPACKのサブルーチ
ン
● MPI 並列
● Faster replacements for ScaLAPACK...
● ScaLAPACKよりも高速 （遅くても2倍以上）
8

9. ELPA 改良点の調査結果
● アルゴリズム・実装・通信手法の改良
– ステップ 1 部分 (3重対角化)
● 二段階の操作
– (i) 密 full → 帯行列化
– (ii) 帯 band → ３重対角化
● ブロックhouseholder変換 ＆ バルジ追跡
● BLAS-3 の使用
● キャッシュブロッキング(cache blocking)：
– カーネルレベルでブロックサイズを指定
● MPI非同期通信の使用
– ステップ 2 部分(D&C)
● 通信体系の改善 9

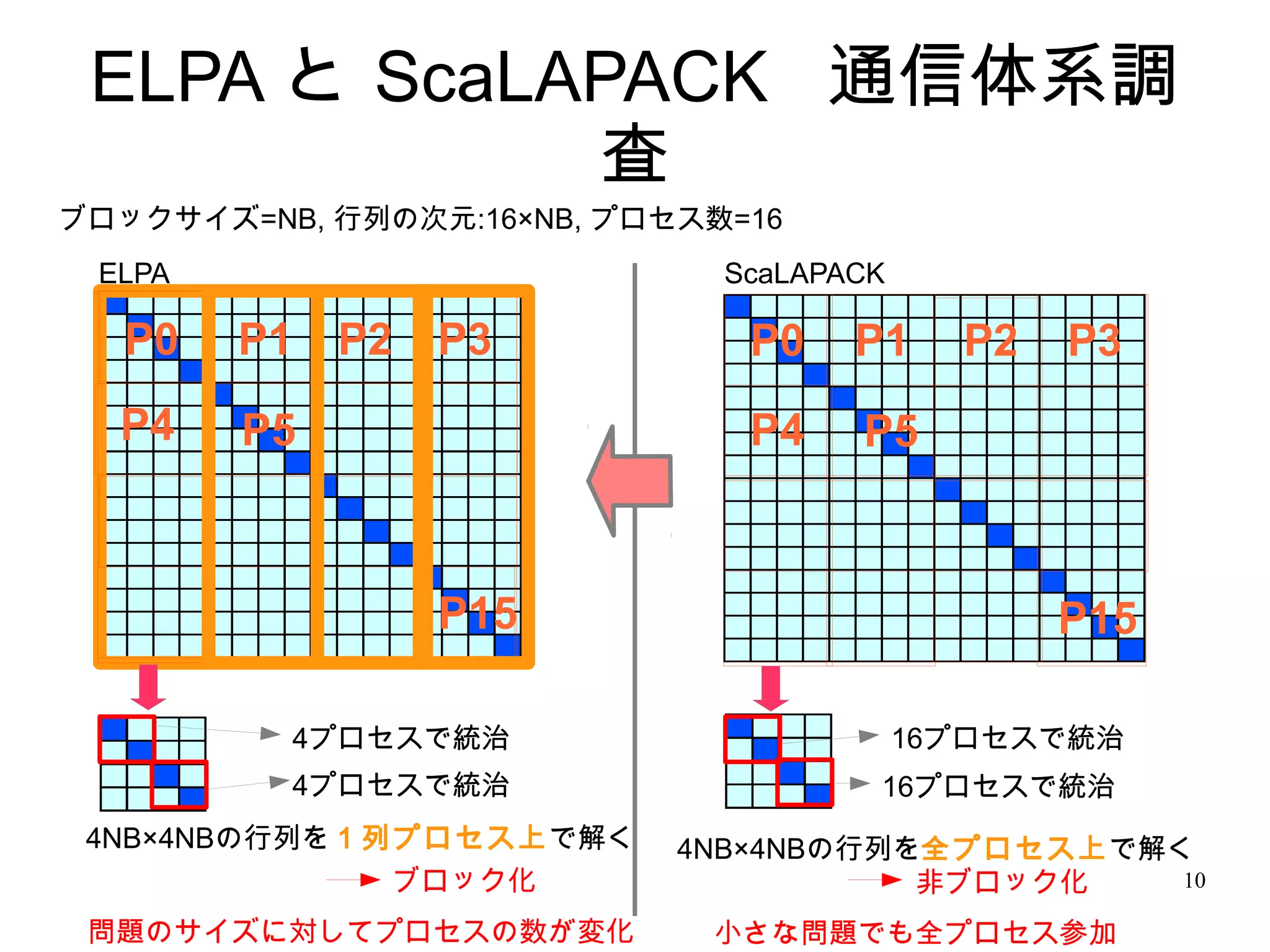
10. ELPA と ScaLAPACK 通信体系調
査
ブロックサイズ=NB, 行列の次元:16×NB, プロセス数=16
ELPA ScaLAPACK
P0 P1 P2 P3 P0 P1 P2 P3
P4 P5 P4 P5
P15 P15
4プロセスで統治 16プロセスで統治
4プロセスで統治 16プロセスで統治
4NB×4NBの行列を１列プロセス上で解く 4NB×4NBの行列を全プロセス上で解く
ブロック化 非ブロック化 10
問題のサイズに対してプロセスの数が変化 小さな問題でも全プロセス参加

11. ELPA と ScaLAPACK 比較実験
● ３重対角D&Cの時間測定 solve_tridi v.s. PDSTEDC
● 実験環境(JED)
– ホスト: JEDのマシン purple(01~30), blue(01~20) を計50台使用
– CPU: Intel(R) Core(TM)2 Duo CPU E8300 @ 2.83GHz
– メモリ: 3598232kB
– OS: Vine Linux 6.0
– コンパイラ: mpif90, 最適化オプション: -O3
● 測定方法
– MPI並列
– 関数呼出しの前後でMPI_Wtime()により時間を測り、その時間差を記録
– 行列のサイズ: 4000, ブロックサイズ:16
11
– マシン数: 4,8,16,19,25,32,41,50台 と変化 (コア数は ”台数×2” )

12. ELPA と ScaLAPACK 比較実験
縦軸： 時間[sec]
横軸： プロセス数
青 ELPA： プロセス数・ノード数の増加に伴い、性能向上
赤 ScaLAPACK： プロセス・ノード数50以降から性能鈍化の傾向 12

13. まとめ
● ELPA：
– マシンを最大限利用 → 性能向上
– 通信手法の工夫：
● プロセスの列ブロック化
●
非同期通信
● ScaLAPACK：
– 性能鈍化の傾向
– 通信時間（同期処理など）の増加
● D&C を 3重→帯行列へ拡張
– ELPAの性能向上率は期待できる 13

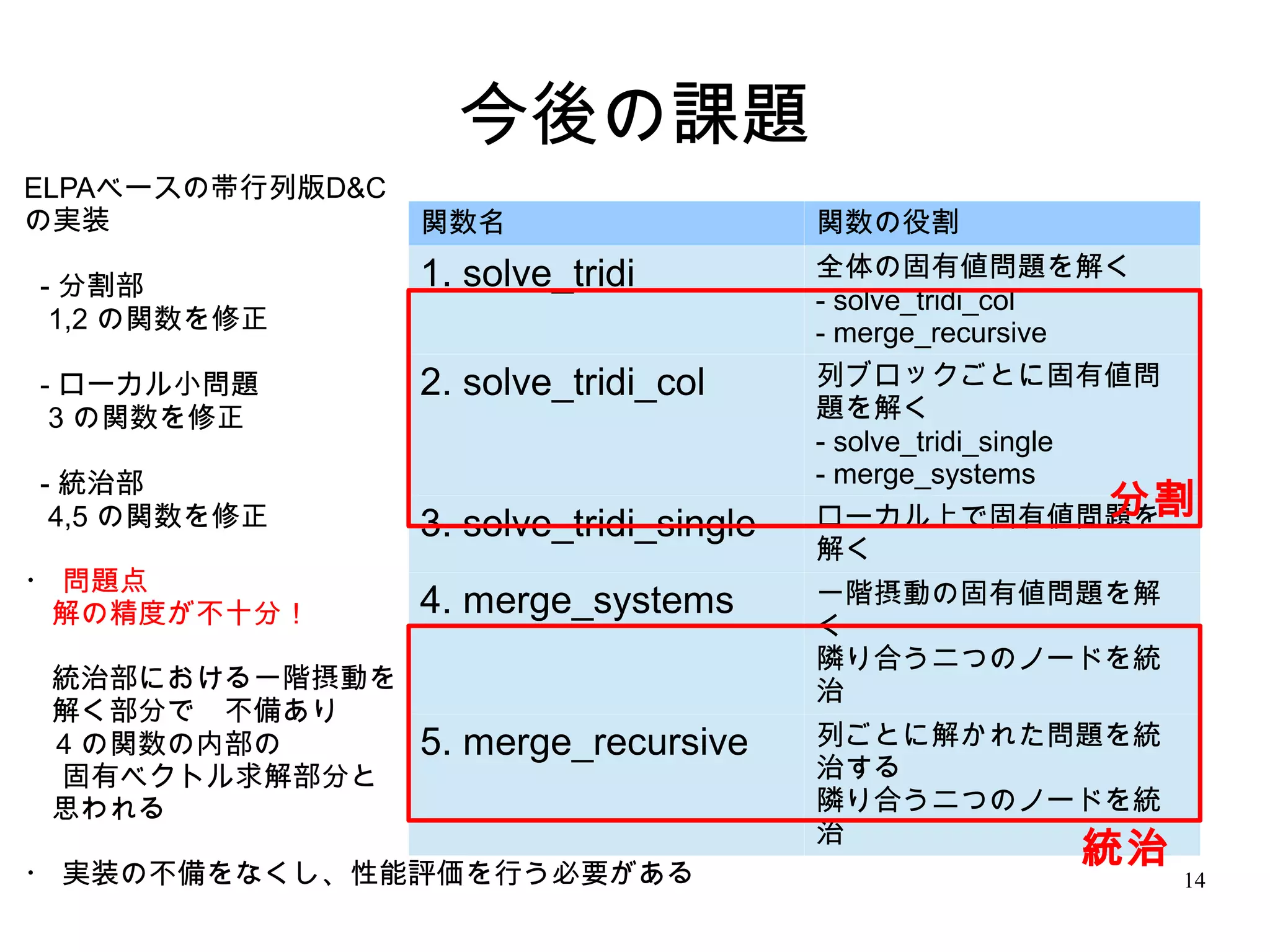
14. 今後の課題
ELPAベースの帯行列版D&C
の実装 関数名 関数の役割
1. solve_tridi 全体の固有値問題を解く
- 分割部 - solve_tridi_col
1,2 の関数を修正 - merge_recursive
- ローカル小問題 2. solve_tridi_col 列ブロックごとに固有値問
3 の関数を修正 題を解く
- solve_tridi_single
- 統治部 - merge_systems
4,5 の関数を修正 ローカル上で固有値問題を 分割
3. solve_tridi_single
解く
・ 問題点 一階摂動の固有値問題を解
解の精度が不十分！ 4. merge_systems
く
隣り合う二つのノードを統
統治部における一階摂動を 治
解く部分で 不備あり
4 の関数の内部の 5. merge_recursive 列ごとに解かれた問題を統
固有ベクトル求解部分と 治する
思われる 隣り合う二つのノードを統
治
統治
・ 実装の不備をなくし、性能評価を行う必要がある 14

15. 参考文献
1. Pham Huu Phuong, 実対称帯行列の固有値問題の分割統治法の提案,
平成22年度電気通信大学電気通信学専攻修士論文
2. T. Auckenthaler, V. Blum, H.-J. Bungartz, T. Huckle, R. Johanni, L.
Krämer, B. Lang, H. Lederer, and P. R. Willems: "Parallel solution of
partial symmetric eigenvalue problems from electronic structure
calculations", Parallel Computing 37, PP.783-794 (2011).
3. http://elpa-lib.fhi-berlin.mpg.de/wiki/index.php/Main Page(ELPA ラ
イブラリフォーラムページ)
4. 桑島豊, 田村純一, 坪谷怜, 重原孝臣, 実対称固有値問題に対する多分
割の分割統治法の分散並列アルゴリズムの提案. 情報処理学会論文誌
コンピューティングシステムVol.3, No.20-29(June 2010)
15

16. 参考文献
5. 馬路徹, GPU アーキテクチャ及びGPU コンピューティング入門. シ
ニア・ソリューション・アーキテクト、NVIDIA ジャパン, GTC
Workshop Japan 2011.
6. 今村俊幸, 並列環境向けの固有値計算アルゴリズムと自動チューニン
グ, The Japan Society for Indus-trial and Applied Mathematics,
Vol.20, No.3, PP.212-222, Sep.2010 (特集：数値計算のための自動
チューニング)
16