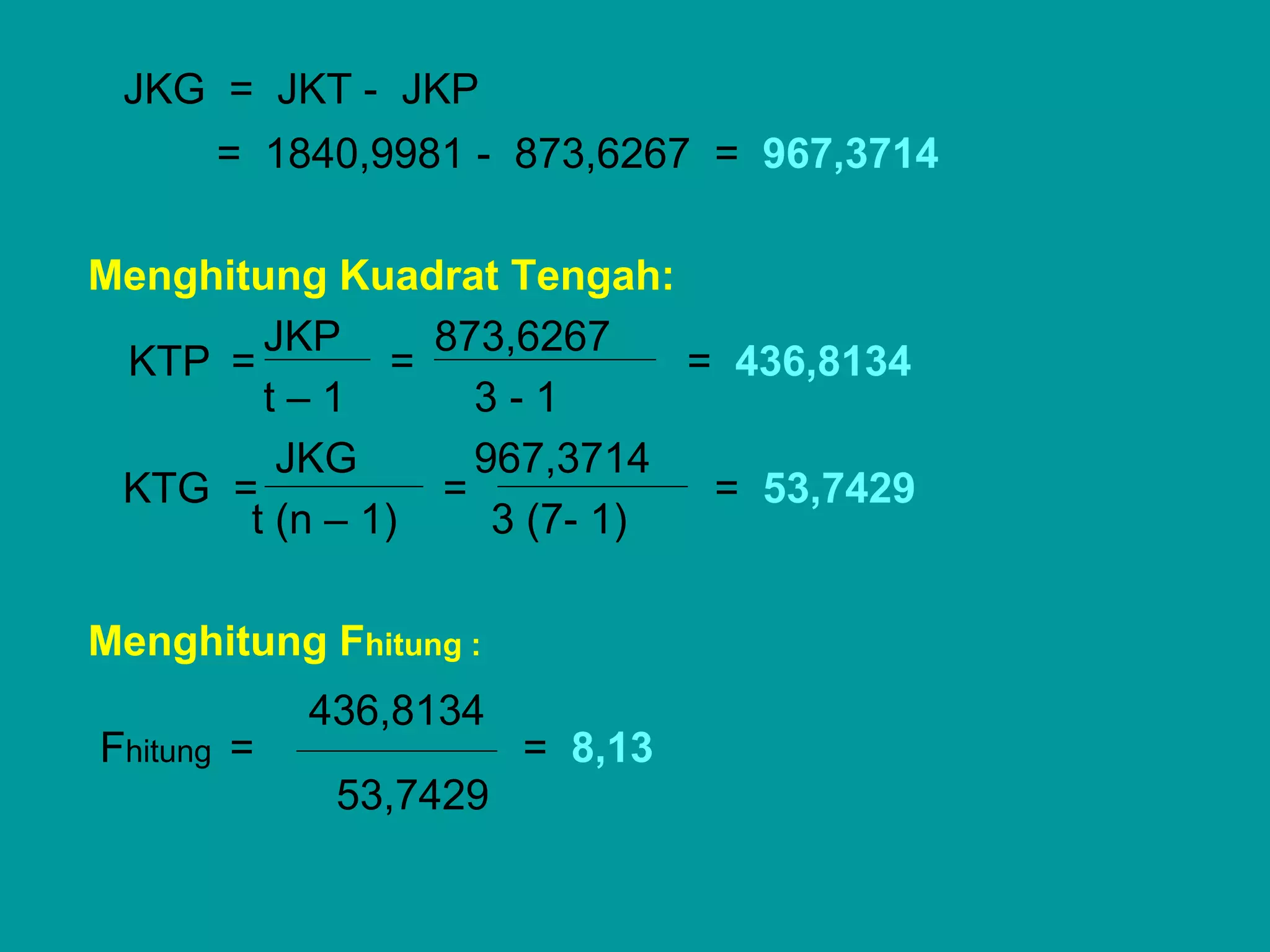
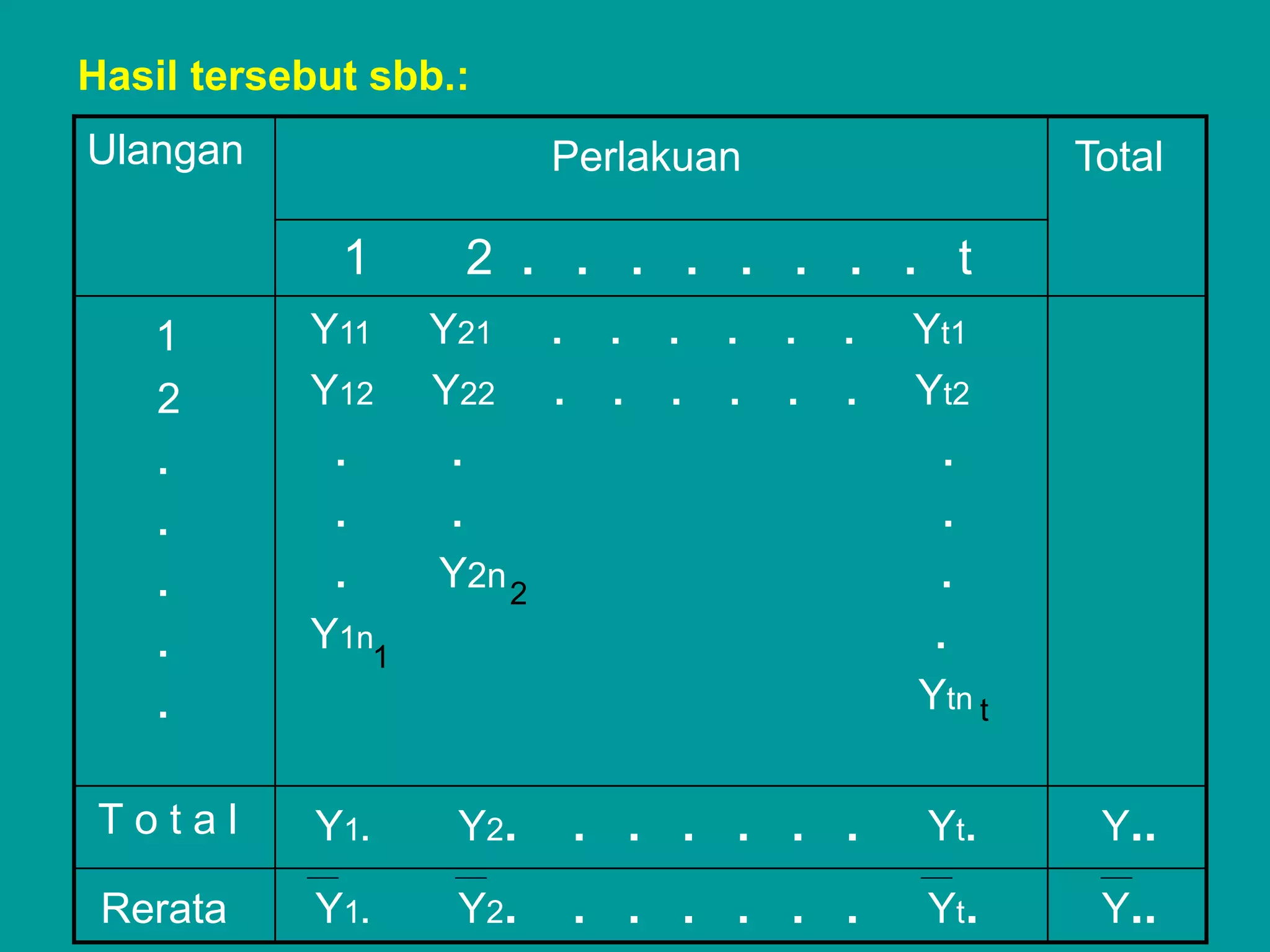
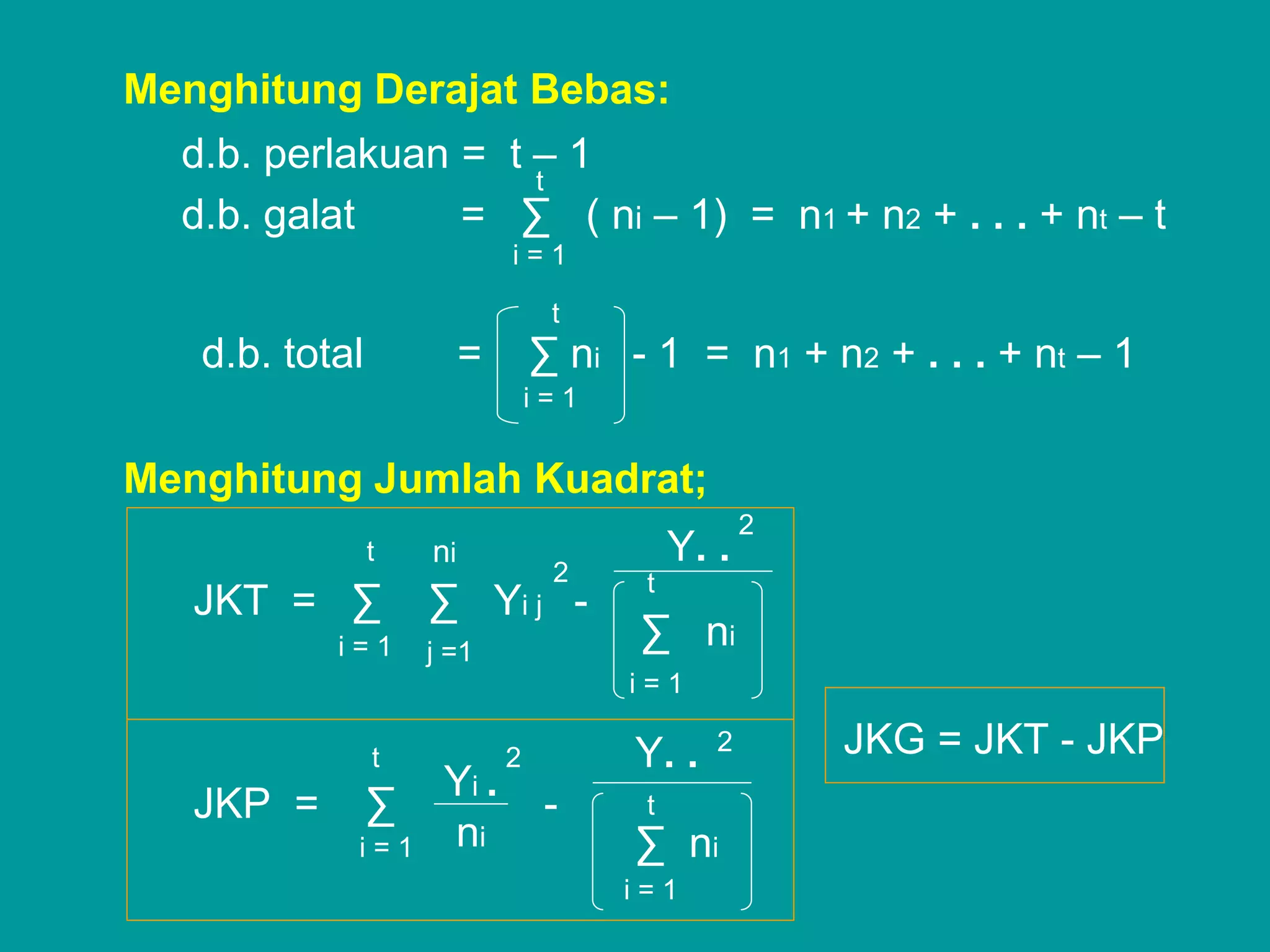
Dokumen ini membahas tentang rancangan acak lengkap (RAL) dalam eksperimen, termasuk ciri-ciri, model matematikanya, dan cara analisis data menggunakan analisis ragam (ANOVA). Contoh penerapan RAL pada penelitian berat badan babi dengan tiga jenis ransum menunjukkan perbedaan signifikan yang memerlukan uji lebih lanjut. Penghitungan derajat bebas, jumlah kuadrat, dan sidik ragam disertakan untuk mendemonstrasikan metode analisis yang tepat.

1. Rancangan Acak Lengkap
(RAL)
Completely Randomized Design
Atau
Fully Randomized Design
(Ir.Zakaria Ibrahim,MM )

2. CIRI - CIRI R.A.L. :
1. Media atau bahan percobaan
―seragam‖ (dapat dianggap se-
ragam )
2. Hanya ada satu sumber kera-
gaman, yaitu perlakuan (disam-
ping pengaruh acak)

3. Model Matematika RAL:
. Yij = μ + Τi + εij i = 1, 2, …… , t
j = 1, 2,………., n
Yij = nilai pengamatan pada perlakuan ke i, ulangan
ke j
μ = nilai tengah umum
Τi = pengaruh perlakuan ke i
εij = pengaruh acak (kesalahan percobaan) pada
perlakuan ke i dan ulangan ke j
t = banyaknya perlakuan
n = banyaknya ulangan

4. ULANGAN pada RAL :
Diperoleh dari: Derajat bebas galat RAL ≥ 15
t ( n – 1 ) ≥ 15 t = banyaknya perlakuan
n = banyaknya ulangan
Contoh: Diketahui jumlah perlakuan yang diberikan = t = 3
Maka ulangan minimal yang diperlukan:
t ( n – 1 ) ≥ 15
3 ( n – 1 ) ≥ 15
3n – 3 ≥ 15
3n ≥ 18 → n = 18/3 = 6

5. t ( n – 1 ) ≥ 15 t = banyaknya perlakuan
n = banyaknya ulangan
Contoh: Diketahui jumlah perlakuan yang diberikan = t = 6
Maka ulangan minimal yang diperlukan:
t ( n – 1 ) ≥ 15
6 ( n – 1 ) ≥ 15
6n – 6 ≥ 15
6n ≥ 21 → n = 21/6 = 3,5
Jadi banyaknya ulangan = minimal 3,5 maka dipakai 4 ulangan

6. • Cara Pengacakan RAL secara acak lengkap
Misalnya: Perlakuan A, B, C, D, E dan F
Ulangan 4 kali A1, A2, A3, A4
B1, B2, B3, B4
C3 B1 D2 A4 E2 A1 dst
D1 F3 A2 C1 F1 B3 diperoleh:
6x4=
24 satuan
B2 F4 E3 D3 B4 C2
percobaan
A3 D4 F2 E1 C4 E4

7. PENGOLAHAN DATA dan SIDIK RAGAM
Percobaan dengan t perlakuan dan n ulangan
Perlakuan
Ulangan Total
1 2 .............. t
1 Y11 Y21 . . . . . . . . . . . . . Yt1
2 Y12 Y22 .
. . . .
. . . .
. . . .
n Y1n Y2n Ytn
Total Y1. Y2. Yt . Y..
Rerata Y1. Y2. Yt . Y..

8. n
t Hasil pengamatan yang mendapat
Y 12 = perlakuan 1 dan ulangan ke 2
i=1 2
Y. .
j=1 Faktor Koreksi = FK = ——
txn
t n 2
JKT = ∑ ∑ Yi j - FK
i=1 J=1
JKG = JKT - JKP
t 2
JKP = ∑ Yi .
─── - FK
n
i=1

9. Sidik Ragam = Analisis Ragam
(Analysis of variance = ANOVA)
Sumber Derajat Jumlah Kuadrat F tabel
Bebas Kuadrat Tengah Fhit 0,05 0.01
Keragaman (d.b.) (J.K.) (K.T.)
( S.K.)
Perlakuan t–1 JKP KTP
Galat t (n –1) JKG KTG
percobaan
Total tn-1 JKT

10. JKP JKG JKT
KTP = —— KTG = —— KTT = ——
t-1 t (n-1) tn–1
KTP
Fhit.= —— KTT ≠ KTP + KTG
KTG
Kemungkinan akan diperoleh:
(1). Fhitung < Ftabel → tidak berbeda nyata
(non significant)
↓
Berarti: - terima H0 ( tolak H1 )
- tidak terdapat perbedaan
di antara perlakuan

11. (2). Fhitung ≥ Ftabel 0,05 → berbeda nyata (significant),
Fhitung ≥ Ftabel 0,01 → berbeda sangat nyata
(highly significant)
↓
Berarti: - terima H1 (tolak H0)
- salah satu atau lebih dari perla-
kuan yang diberikan, berbeda
dengan perlakuan yang lain
Perlu uji lebih lanjut
untuk menentukan perlakuan-perlakuan mana
yang berbeda nyata satu sama lain

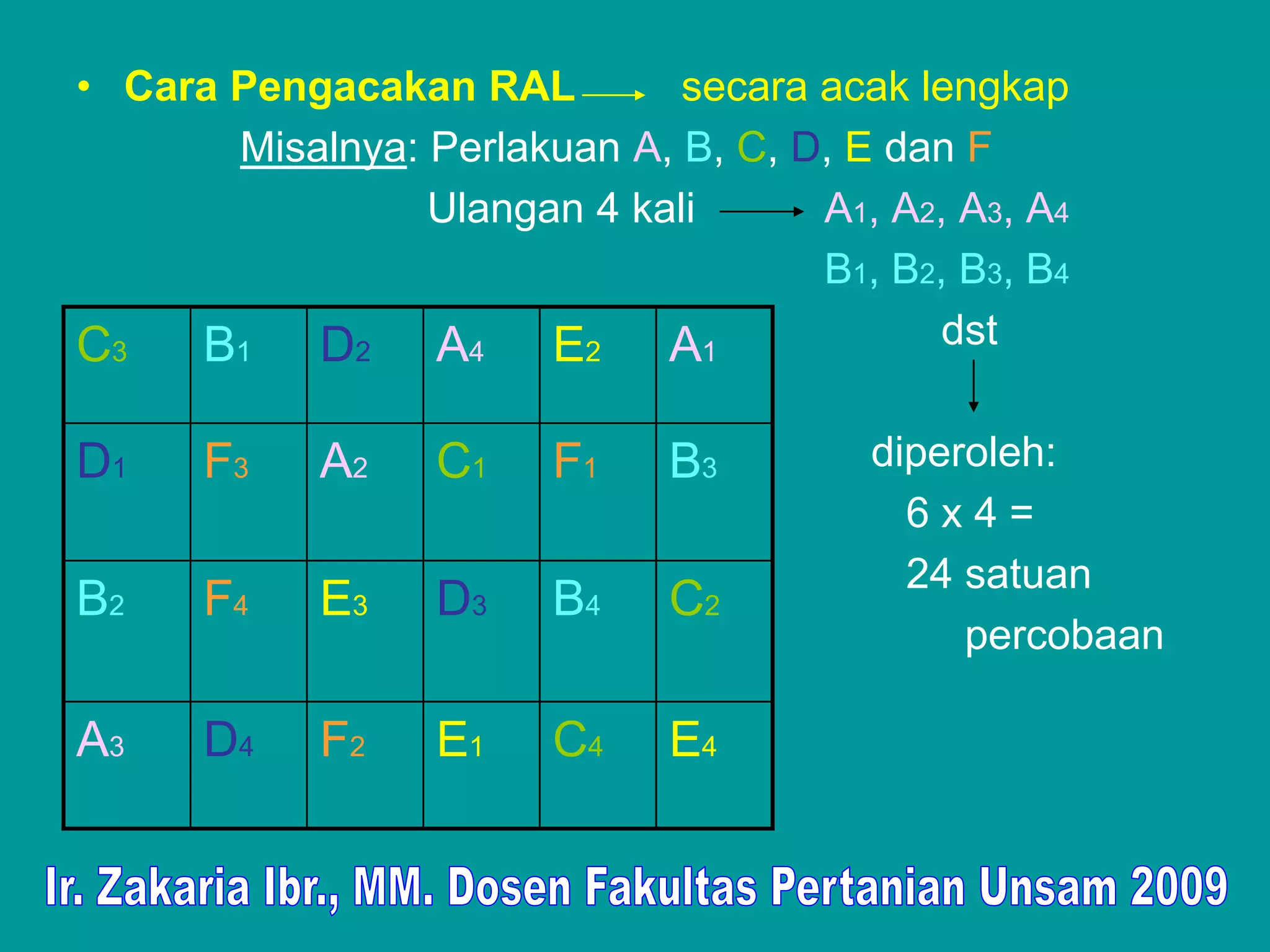
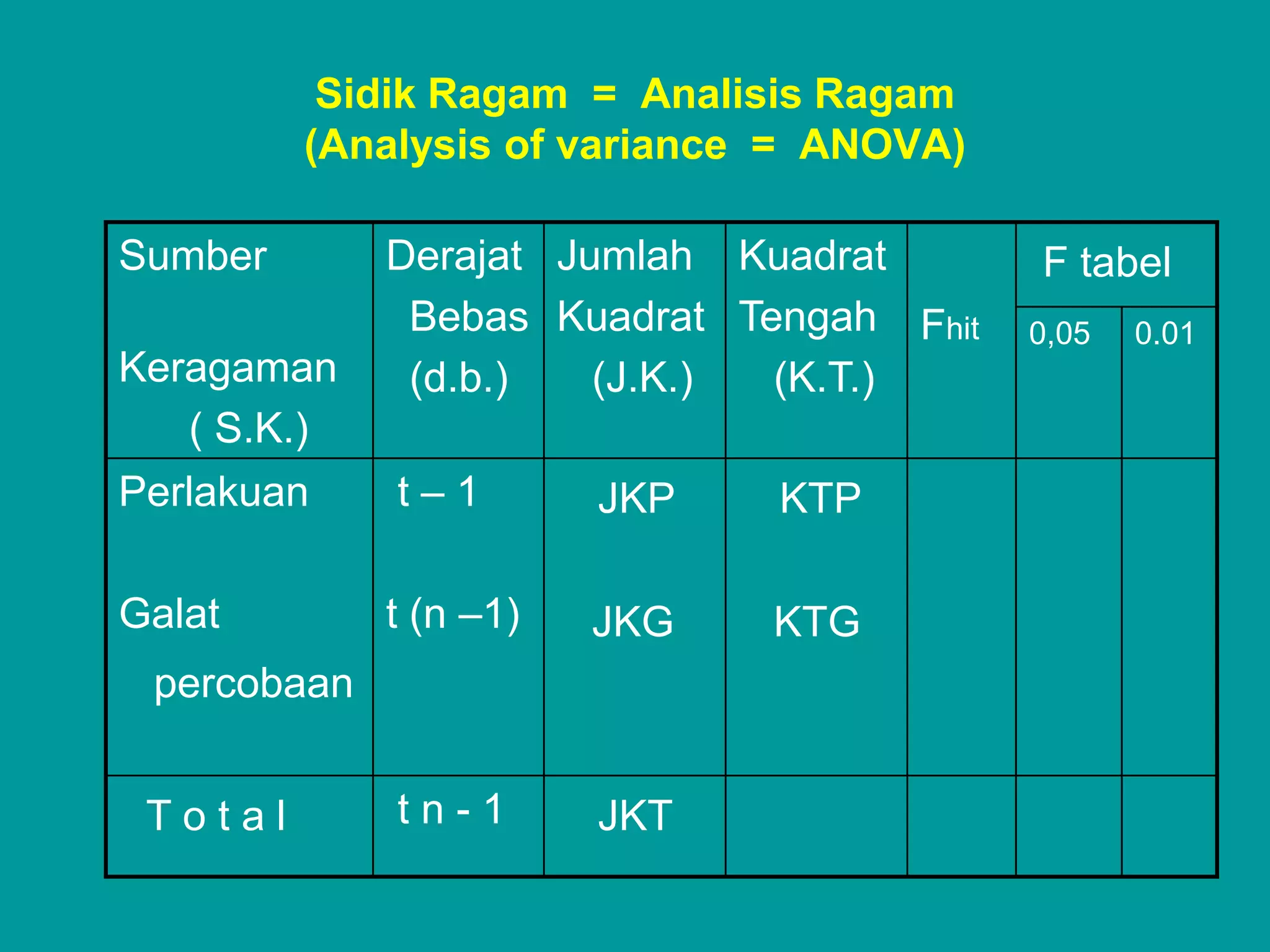
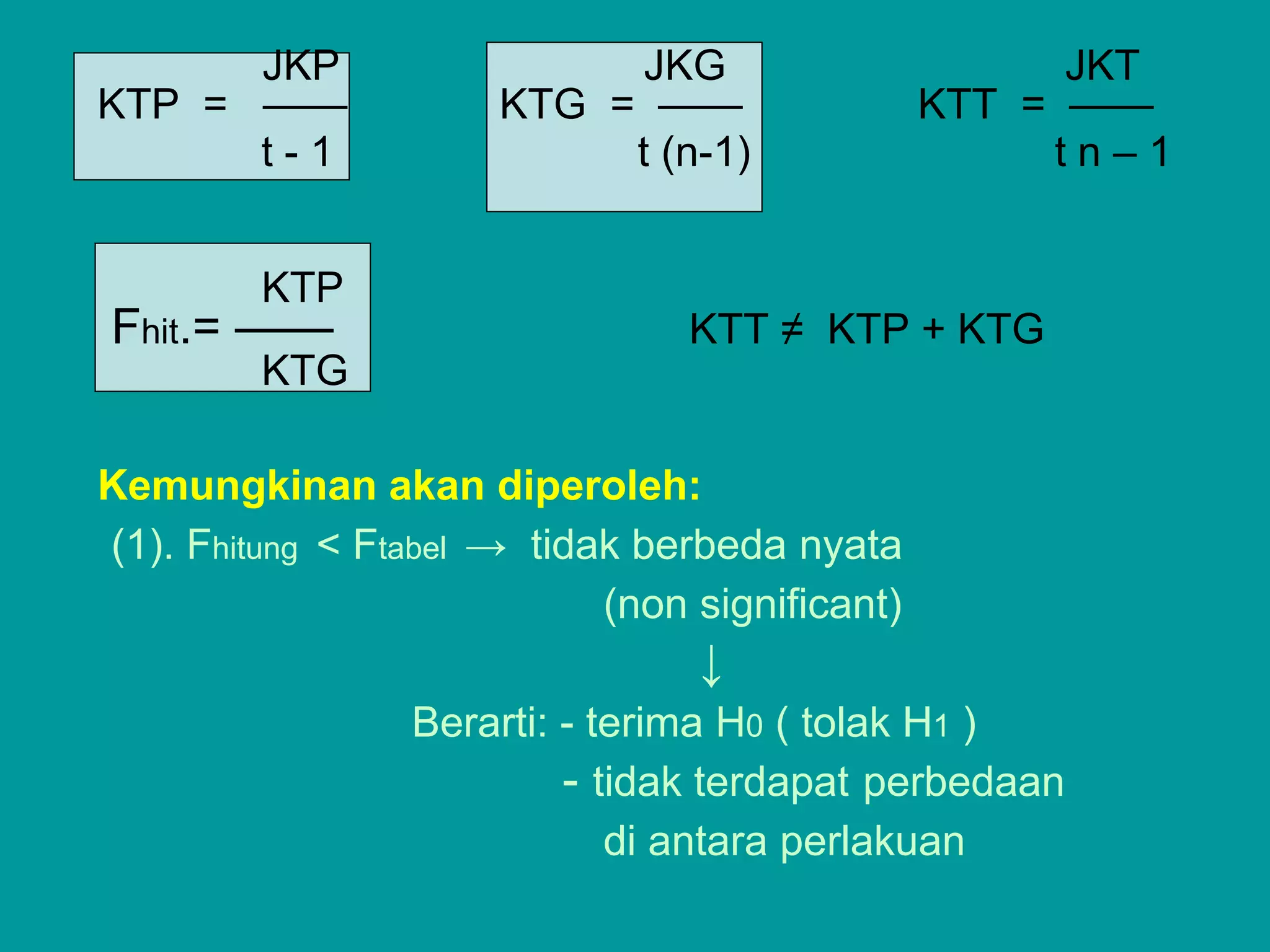
12. Contoh: Penelitian menggunakan RAL dan
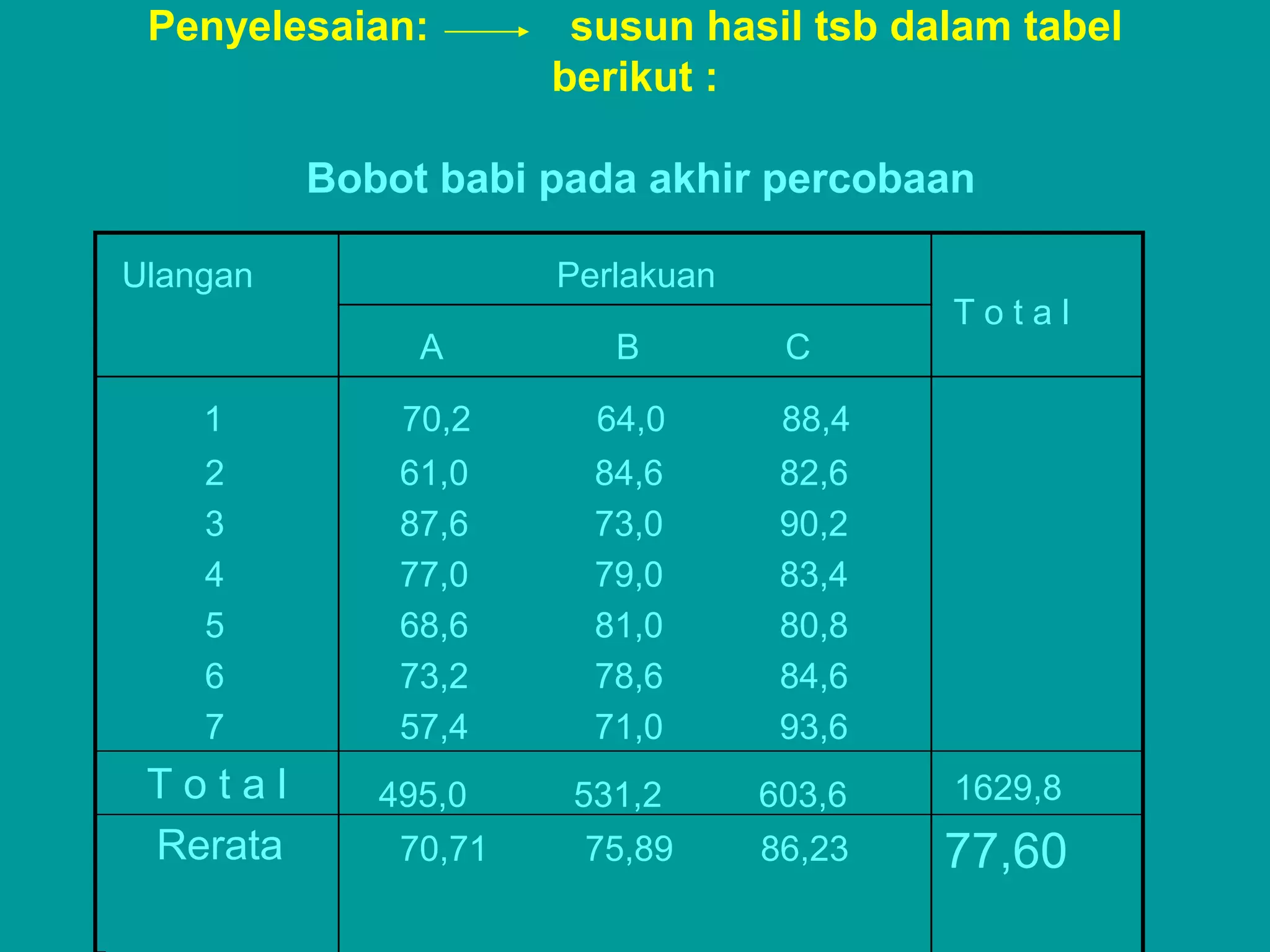
Cara pengolahan hasilnya
Penelitian ingin mengetahui pengaruh 3 macam ransum:
A = ransum setempat
B = ransum + 0,1% Pfizer Penicilin Feed Supplement
C = ransum + 0,1% Pfizer Teramycin Animal Mix
terhadap berat badan ternak babi.
Tersedia anak-anak babi umur 4½ bulan, sebanyak 21
ekor dilahirkan pada waktu yang sama, dengan keadaan
yang ―seragam‖ ( jantan semua, dan dengan berat
badan yang relatif sama)
[Dalam hal ini semua ―sama‖ kecuali perlakuan → RAL ]

13. - Rancangan acak lengkap dgn: perlakuan = t = 3
ulangan = n = 21/3 = 7
-Hasil pengacakan yang dilakukan:
A2 B3 C7 B6 A4 C5 B2
C6 B4 A5 C4 B1 A3 C1
C3 A1 B7 A6 C2 B5 A7

14. Model umum matematika penelitian:
Yi j = μ + i + εi j dengan: i = 1, 2, 3.
j = 1, 2, . . . .. 7
Yi j = bobot babi yang menerima perlakuan ransum ke i
pada ulangan ke j
μ = nilai tengah umum
i = pengaruh perlakuan ransum ke I
εi j = pengaruh acak (kesalahan percobaan) pada
perlakuan ransum ke I dan ulangan ke j
Hasil penelitian → Bobot babi pada akhir penelitian:
(A): 70,2; 61,0; 87,6; 77,0; 68,6; 73,2 dan 57,4 kg
(B): 64,0; 84,6; 73,0; 79,0; 81,0; 78,6 dan 71,0 kg
(C): 88,4; 82,6; 90,2; 83,4; 80,8; 84,6 dan 93,6 kg

15. Penyelesaian: susun hasil tsb dalam tabel
berikut :
Bobot babi pada akhir percobaan
Ulangan Perlakuan
Total
A B C
1 70,2 64,0 88,4
2 61,0 84,6 82,6
3 87,6 73,0 90,2
4 77,0 79,0 83,4
5 68,6 81,0 80,8
6 73,2 78,6 84,6
7 57,4 71,0 93,6
Total 495,0 531,2 603,6 1629,8
Rerata 70,71 75,89 86,23 77,60

16. Menghitung Jumlah Kuadrat:
2
2
y .. (1629,8)
F.K. = ─── = = 126488,0012
nxt 7x3
t n 2
JKT = ∑ ∑ Yi j - FK
i=1 j=1
2 2 2
= (70,2) + (61,0) + . . . . . . + (93,6) - FK
= 1840,9981
t 2
Yi .
JKP = ∑ ─── - FK
i=1
n
2 2 2
(495,0) + (531,2) + (603,6) - FK
=
7
= 873,6267

17. JKG = JKT - JKP
= 1840,9981 - 873,6267 = 967,3714
Menghitung Kuadrat Tengah:
JKP 873,6267
KTP = = = 436,8134
t–1 3-1
JKG 967,3714
KTG = = = 53,7429
t (n – 1) 3 (7- 1)
Menghitung Fhitung :
436,8134
Fhitung = = 8,13
53,7429

18. Sidik Ragam pengaruh Perlakuan terhadap bobot babi
S.K. d.b. J. K K.T. Fhitung F tabel
0,05 0,01
Perla-
kuan 2 873,6267 436,8134 8,13** 3,55 6,01
Galat 18 967,3714 53,7429
Total 20 1840,9981
Fhitung > Ftabel 0,01 terdapat perbedaan sangat nyata
↓
Tiga macam ransum pakan (A, B dan C)
memberikan perbedaan yang sangat
nyata terhadap bobot babi

19. Ransum pakan mana yang paling baik pengaruhnya
terhadap bobot babi? → Perlu uji lebih lanjut dengan
Uji Pembandingan Berganda:
- Uji BNT
- Uji BNJ
KOEFISIEN KERAGAMAN: - Uji Jarak Duncan
K.K.= s x 100% = √ KTG x 100%
y. . y. .
√53,7429
= x 100% = 9,45%
1629,8 7 x 3
< (15 – 20%)
(Kemungkinan terdapat kesalahan da-
lam pengamatan atau pencatatan data)

20. Percobaan memakai R.A.L. → memungkinkan perlakuan
perlakuan yang diberikan mempunyai jumlah ulangan
tidak sama.
Suatu percobaan dilaksanakan dengan Rancangan Acak
Lengkap, dengan t perlakuan dan ulangan untuk:
perlakuan 1 mendapat sebanyak n1 ulangan,
perlakuan 2 mendapat sebanyak n2 ulangan,
perlakuan 3 mendapat sebanyak n3 ulangan,
. .
. .
perlakuan t mendapat sebanyak nt ulangan.

21. Hasil tersebut sbb.:
Ulangan Perlakuan Total
1 2 . . . . . . . . t
1 Y11 Y21 . . . . . . Yt1
2 Y12 Y22 . . . . . . Yt2
. . . .
. . . .
. . Y2n 2 .
. Y1n1 .
. Ytn t
Total Y1. Y2. . . . . . . Yt. Y..
Rerata Y1. Y2. . . . . . . Yt. Y..

22. Menghitung Derajat Bebas:
d.b. perlakuan = t – 1
t
d.b. galat = ∑ ( ni – 1) = n1 + n2 + . . . + nt – t
i=1
t
d.b. total = ∑ ni - 1 = n1 + n2 + . . . + nt – 1
i=1
Menghitung Jumlah Kuadrat;
2
t ni Y. .
2 t
JKT = ∑ ∑ Yi j -
i=1 j =1
∑ ni
i=1
t 2 Y. . 2 JKG = JKT - JKP
Yi .
JKP = ∑ - t
i=1 ni ∑ ni
i=1

23. Sidik Ragam untuk RAL dengan ulangan tak sama
Ftabel
S.K. d.b. J.K. K.T. Fhitung 0,05 0,01
Perla-
kuan t - 1 JKP KTP
t
Galat ∑ ( ni – 1) JKG KTG
i=1
t
Total ∑ ni - 1 JKT
i=1

24. Menghitung Kuadrat Tengah & Fhitung:
JKP JKG
KTP = KTG = t
t–1
∑ ( ni – 1)
i=1
KTP
Fhitung =
KTG
Contoh soal :
Percobaan pada tikus, dengan 4 macam perlakuan ransum
yang berbeda. Percobaan dilaksanakan dengan RAL. Pa-
da akhir percobaan pertambahan berat badan tikus (dalam
gram) sebagai berikut:

25. Pertambahan Berat Badan Tikus (gram)
Ulangan Perlakuan Total
A B C D
1 3,42 3,17 3,34 3,64
2 3,96 3,63 3,72 3,93
3 3,87 3,38 3,81 3,77
4 4,19 3,47 3,66 4,18
5 3,58 3,39 3,55 4,21
6 3,76 3,41 3,51 3,88
7 3,84 3,55 3,96
8 3,44 3,91
Total 26,62 27,44 21,59 31,48 107,13
Rerata 3,80 3,43 3,60 3,94 14,77

26. Apakah terdapat perbedaan nyata dari pengaruh pembe-
rian ke-4 macam ransum terhadap pertambahan berat
badan tikus tersebut?
2
Penyelesaian: y. . 2
(107,13)
Faktor Koreksi = FK = t = 7+8+6+8
∑ ni
2
i=1 (107,13)
=
29
2 2 2
JKT = (3,42) + (3,96) + . . . . + (3,91) - FK = 2,061
2 2
(26,62) (27,44) (21,59)2 (31,48) 2
JKP = + + + FK = 1,160
7 8 6 8
JKG = 2,061 - 1,160 = 0,901

27. d.b. perlakuan = 4 – 1 = 3
d.b. galat = (7 + 8 + 6 + 8) – 4 = 25
d.b. total = ( 7 + 8 + 6 + 8) – 1 = 28
Sidik ragam:
S.K. d.b. J.K. K.T. Fhitung F tabel
0,05 0,01
Perlakuan 3 1,160 0,387 10,75 ** 2,99 4,68
Galat 25 0,901 0,036
Total 28 2,061
Kesimpulan: Ke-4 ransum tersebut berpengaruh sangat nya-
ta terhadap pertambahan berat badan tikus.

28. Mencari Nilai Ftabel 0.05 dengan Interpolasi:
Untuk: d.b.perlakuan = 12 dalam daftar tabel F
d.b. sisa (galat) = 35 tidak tercantum
↓
d.b. d.b. perlakuan perlu dilakukan
galat 10 12 interpolasi
0,05 0,01
1 .
2 . selisih dari 34 ke 35 =
. . ¼ x 0,03 = 0,0075
. . = 0,01
34 selisih 1 2,05
4 35 ? Selisih 0,03 Jadi nilai dari 35 =
38 selisih 3 2,02 2,05 – 0,01 = 2,04

29. ANALISIS PARAMETRIK & NON PARAMETRIK
Nominal
Tidak Normal Non
Parametrik
Ordinal
Tidak
Normal Transformasi
Interval
Periksa Mendekati Parametrik
Normalitas Normal
Ratio

30. ANALISIS PARAMETRIK ANALISIS NON
PARAMETRIK
1. Uji t berpasangan Wilcoxon test
2. Uji t tidak berpasangan Mann – Whitney test
3. Rancangan Acak Lengkap Uji Kruskal Wallis
4. Rancangan Acak Kelompok Uji Friedman
5. Rancangan Bujursangkar Latin
6. Percobaan Faktorial

31. TUGAS PEKERJAAN RUMAH
P E R LAK UAN
Ulangan
P Q R S T
1 2,2 2,4 3,0 2,8 2,6
2 2,1 2,4 2,9 3,1 2,5
3 1,9 2,3 2,9 2,9 2,6
4 2,1 2,5 3,1 3,0 2,4

33. Ir. Zakaria Ibrahim, MM
JL. A. Yani Lr Utama II No. 35C
 085262794035
PB Seuleumak Langsa
http://zakariaib.multiply.com
http://rancob.web.id
e- mail zakariaib@gmail.com
jack_atim@yahoo.co.id
jack-atim@plasa.com