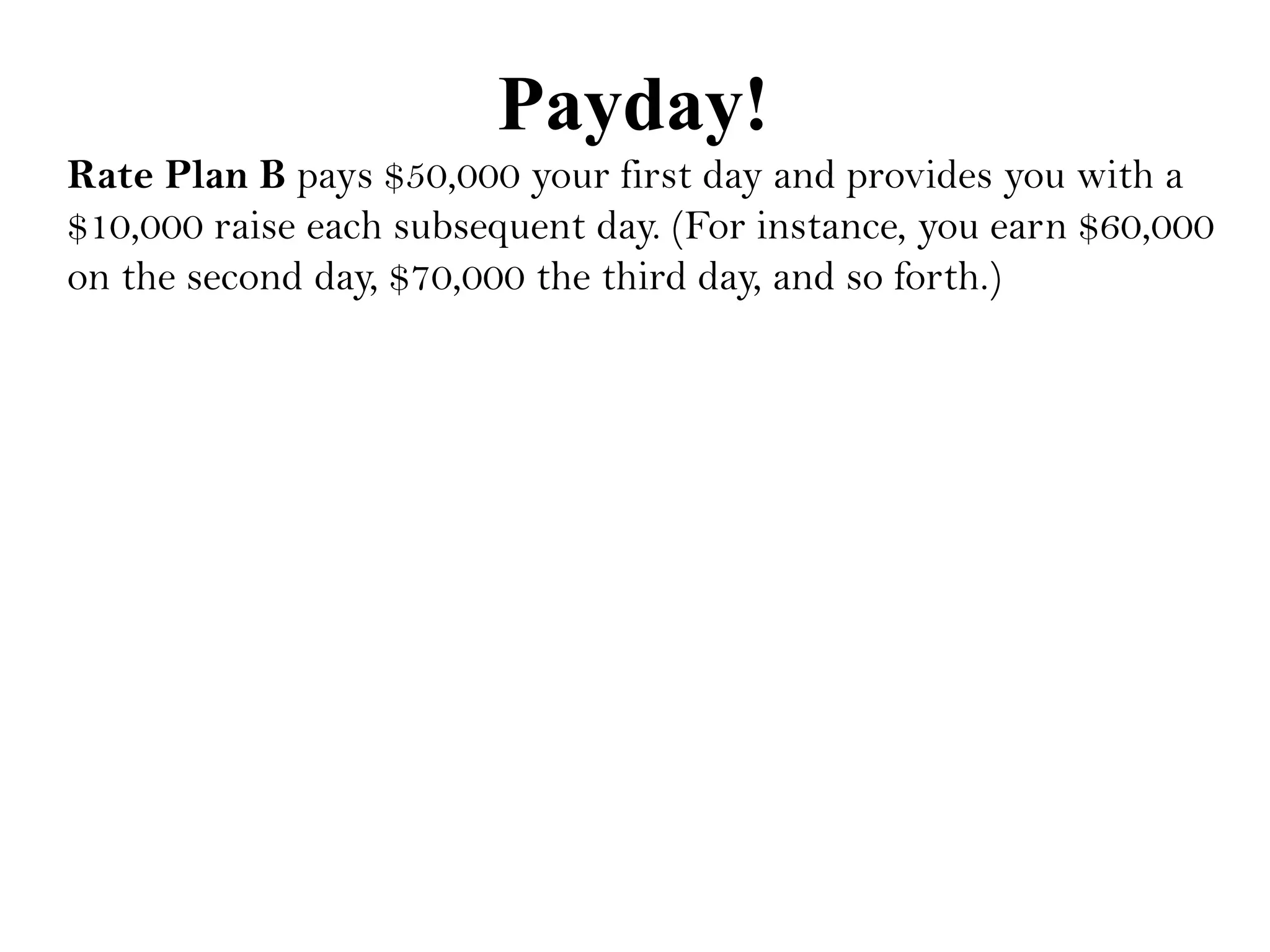
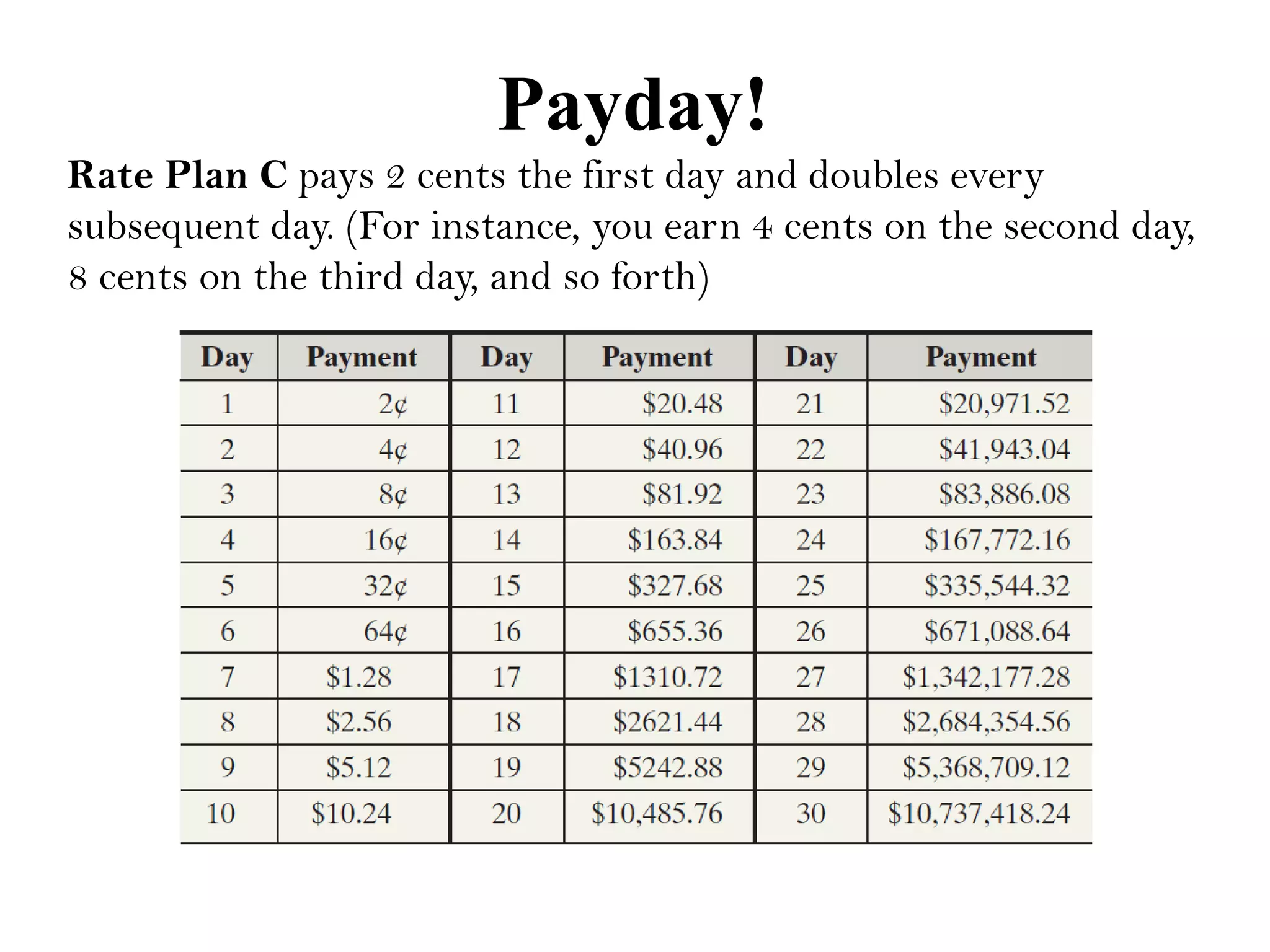
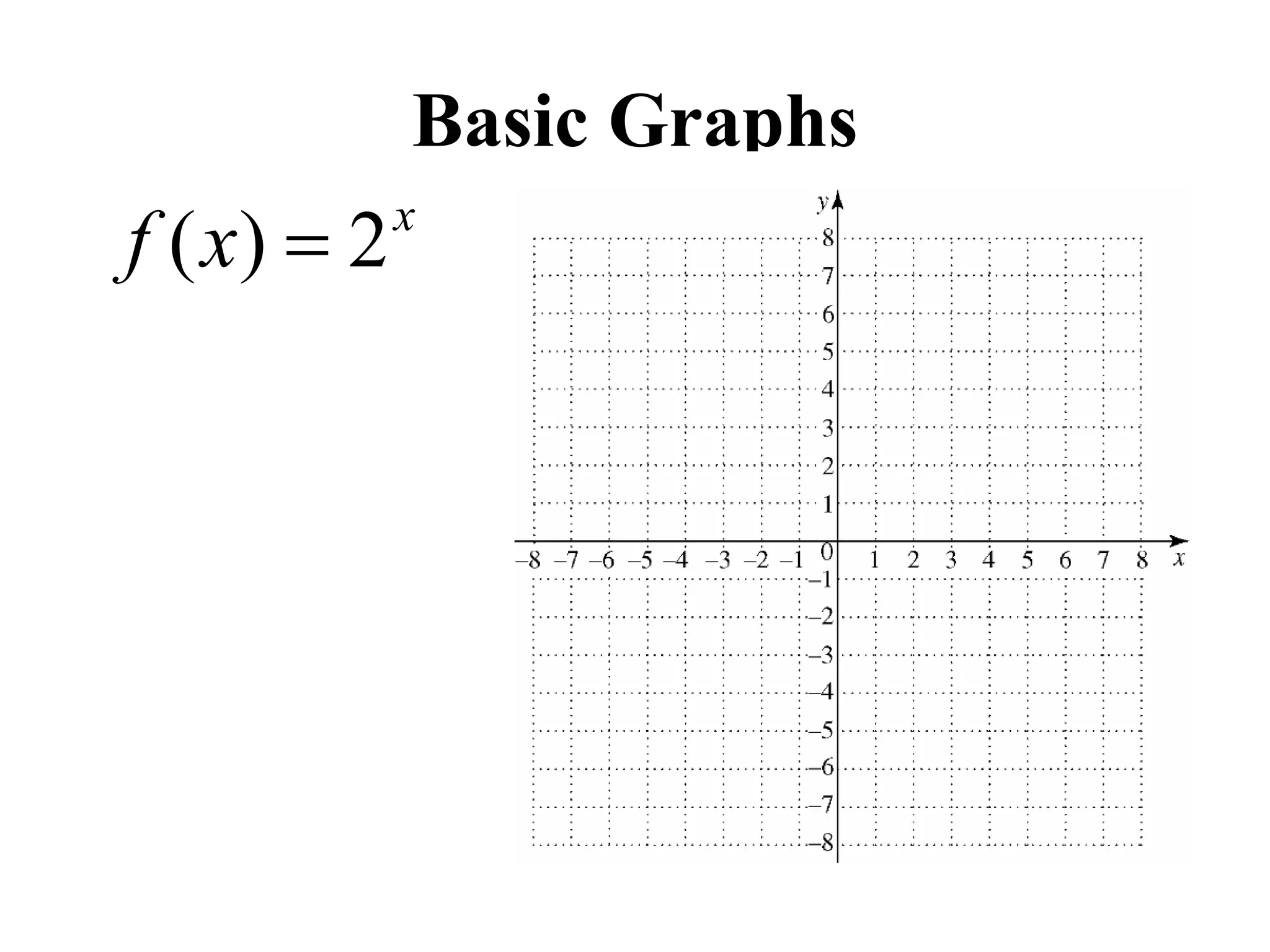
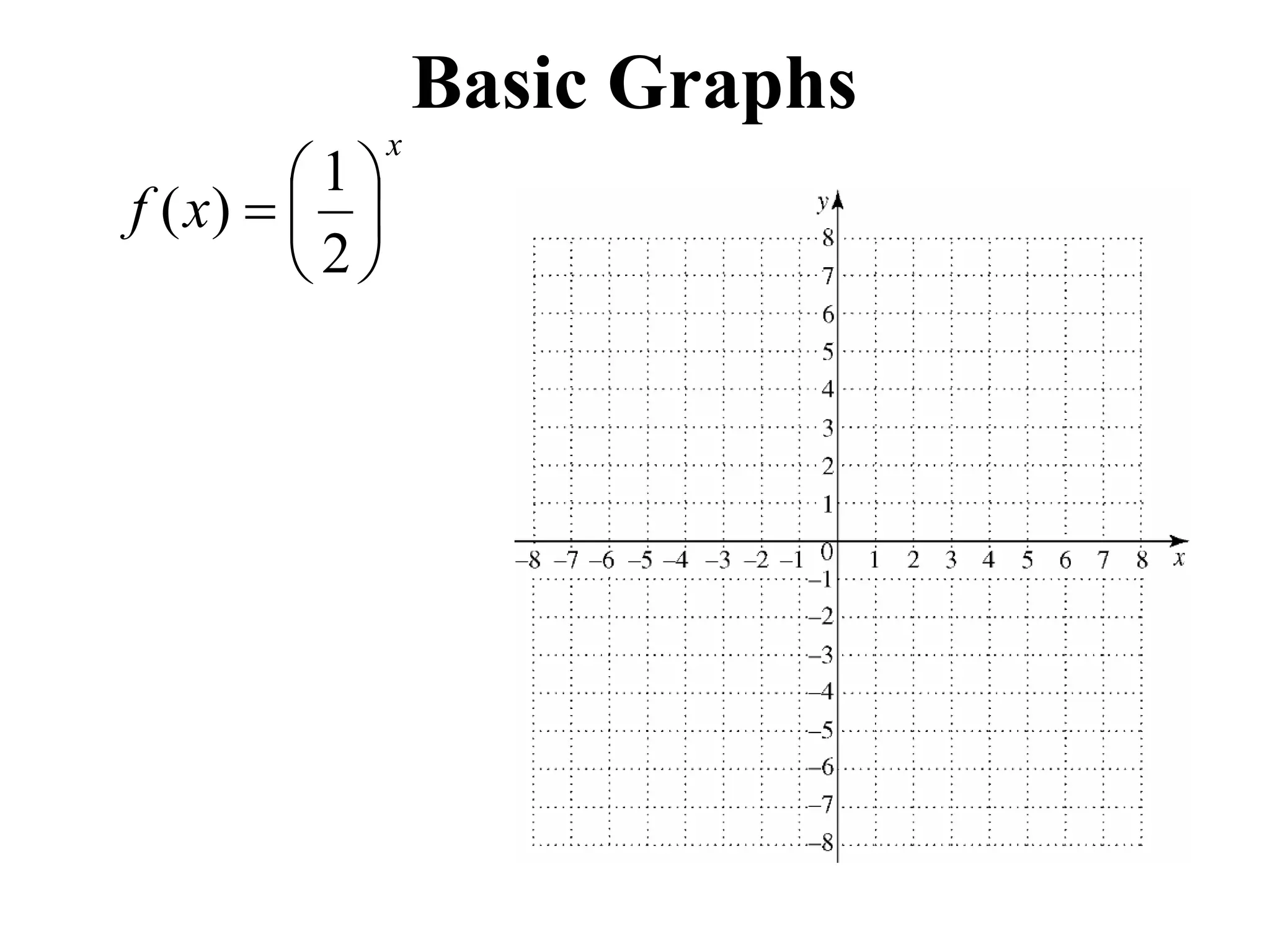
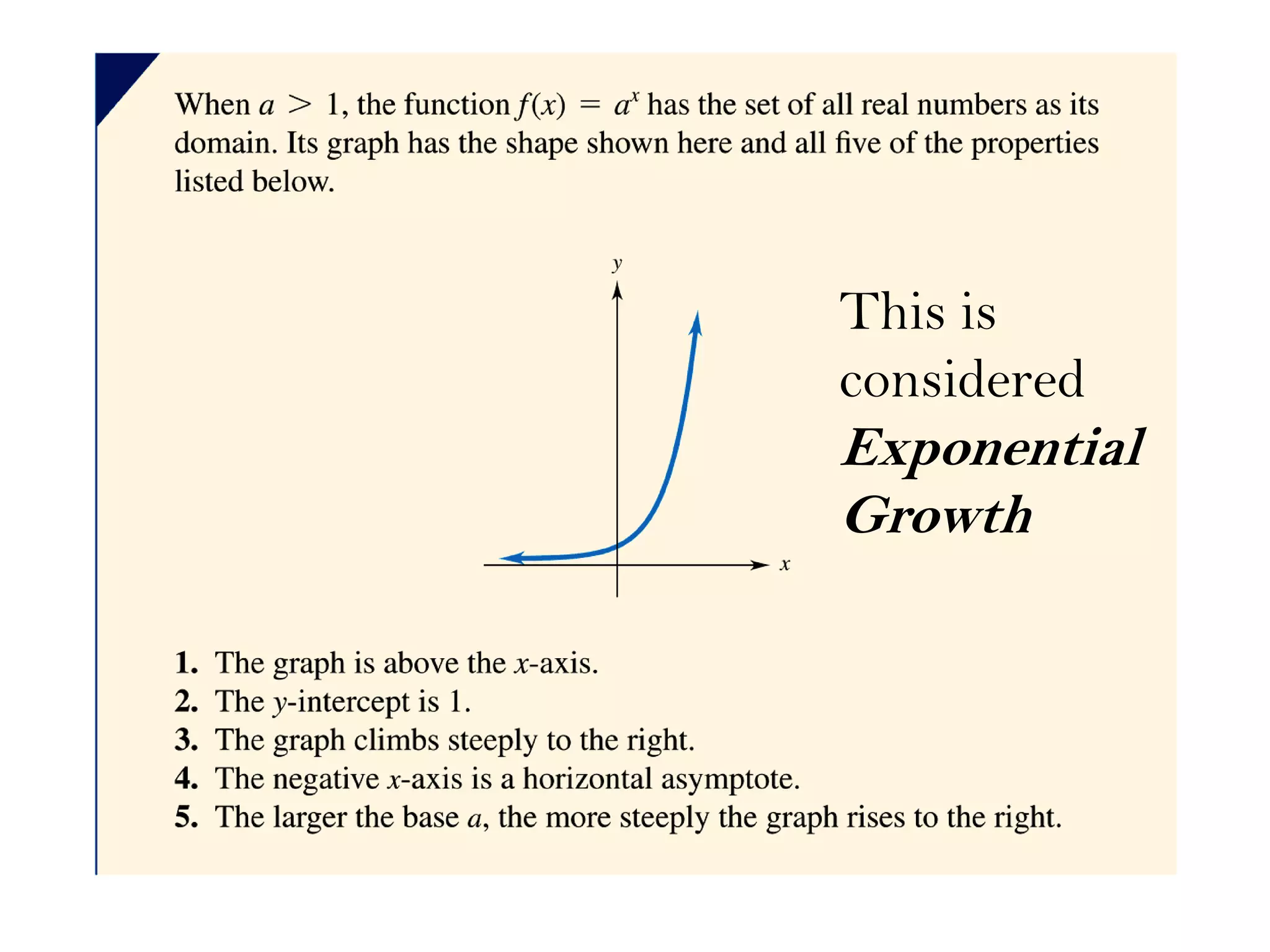
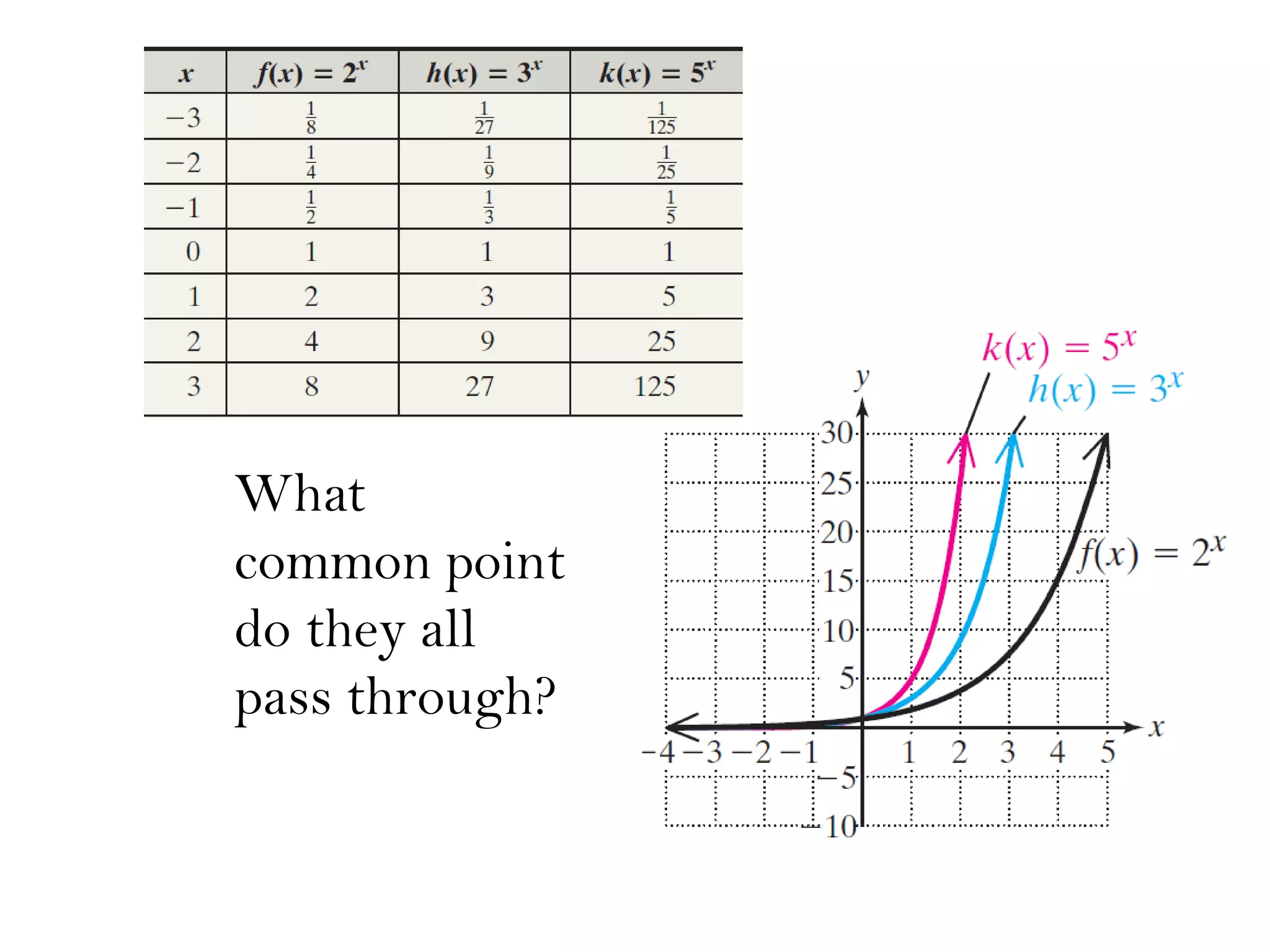
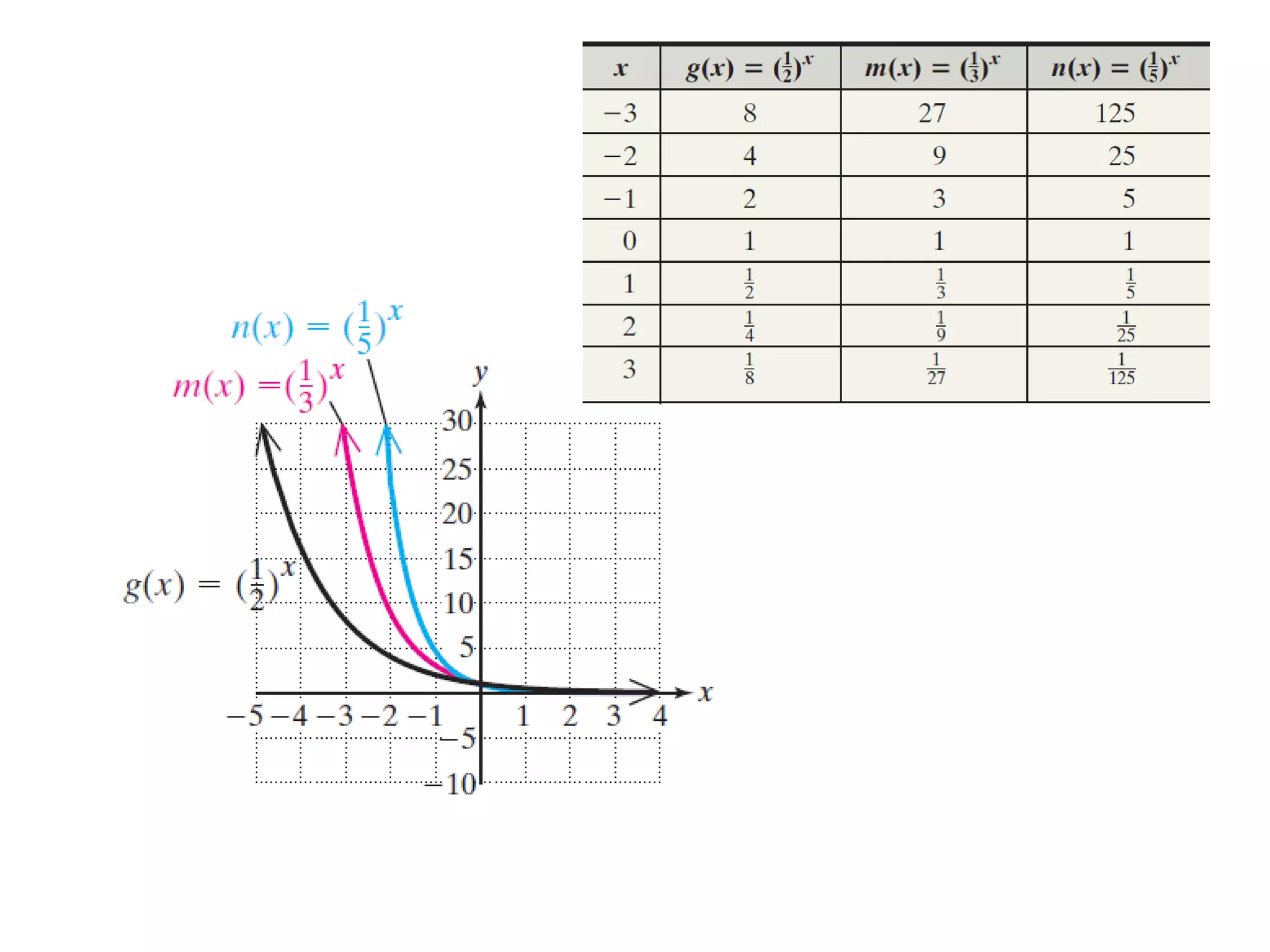
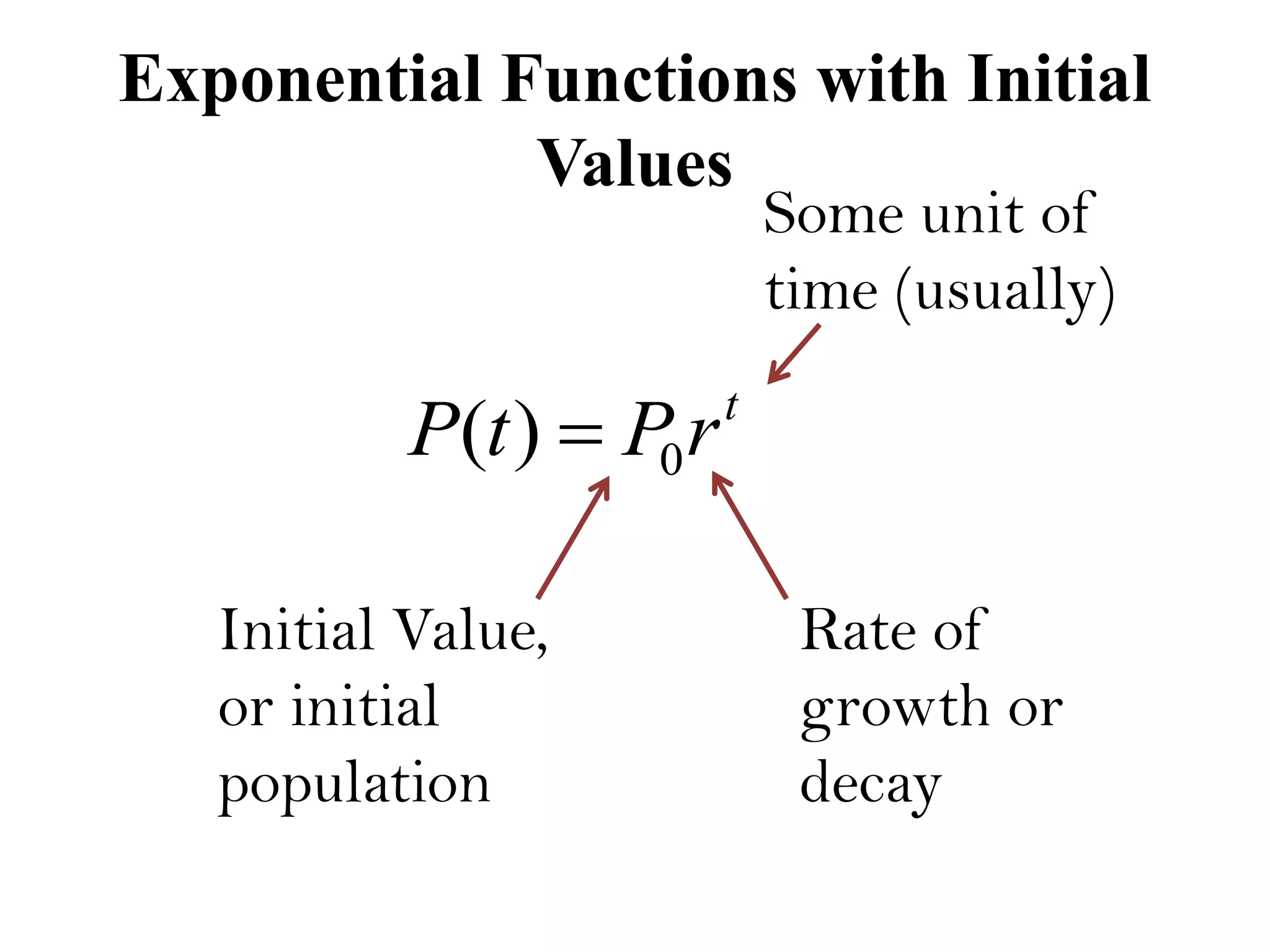
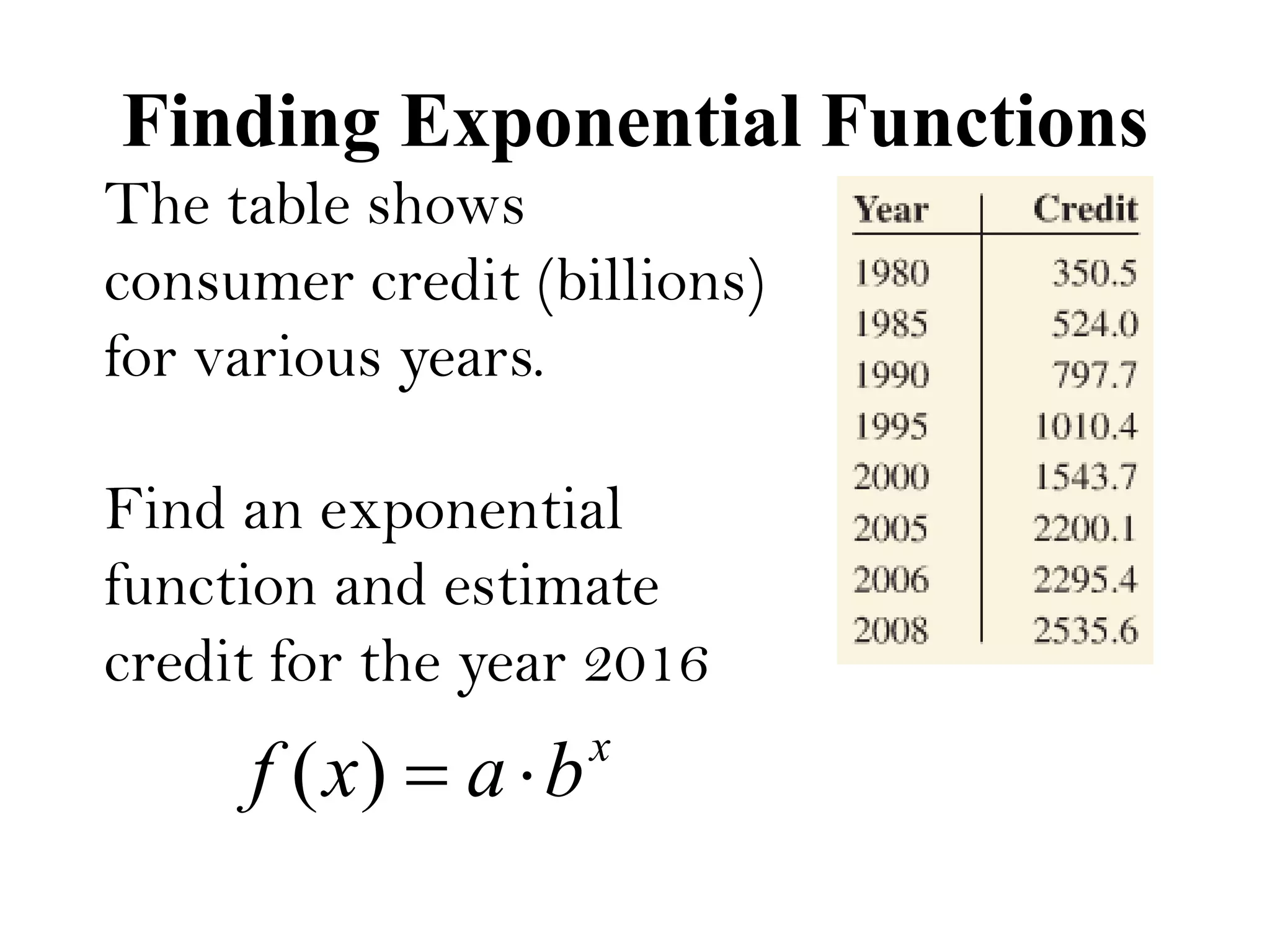
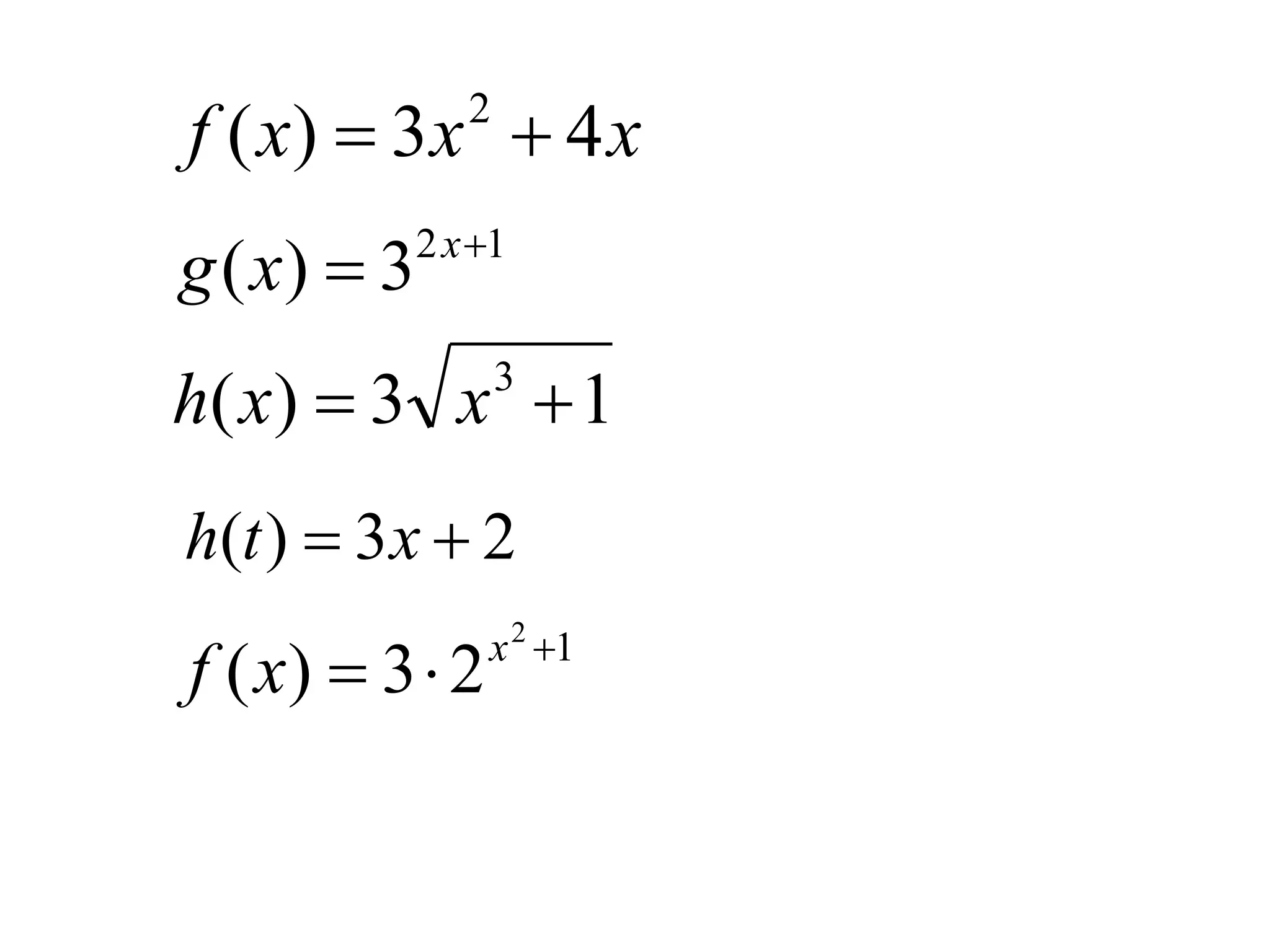The document outlines an agenda for today which includes attendance, submitting projects, covering a section, homework due on Sunday, and a quiz on Monday. It then provides three pay rate plans - Plan A pays $200,000 per day, Plan B starts at $50,000 and increases by $10,000 each day, and Plan C starts at 2 cents and doubles each day. Finally, it discusses exponential functions, including basic graphs, functions with initial values, and examples of finding exponential functions from data points.

1. Today’s Agenda
 Attendance / Announcements
 Submit Projects
 Section 4.1
 MyLabsPlus Homework due Sun.
 E.C. Quiz Monday

2. Payday!
You just got a job! You will work for 30 days. You may
choose between three pay rates.
Rate Plan A pays $200,000 a day.
Rate Plan B pays $50,000 your first day and provides
you with a $10,000 raise each subsequent day. (For
instance, you earn $60,000 on the second day, $70,000 the
third day, and so forth.)
Rate Plan C pays 2 cents the first day and doubles every
subsequent day. (For instance, you earn 4 cents on the
second day, 8 cents on the third day, and so forth)

3. Payday!
Rate Plan A pays $200,000 a day.

4. Payday!
Rate Plan B pays $50,000 your first day and provides you with a
$10,000 raise each subsequent day. (For instance, you earn $60,000
on the second day, $70,000 the third day, and so forth.)

5. Payday!
Rate Plan C pays 2 cents the first day and doubles every
subsequent day. (For instance, you earn 4 cents on the second day,
8 cents on the third day, and so forth)

6. Payday!
Rate Plan C pays 2 cents the first day and doubles every
subsequent day. (For instance, you earn 4 cents on the second day,
8 cents on the third day, and so forth)

7. Payday!
Rate Plan C pays 2 cents the first day and doubles every
subsequent day. (For instance, you earn 4 cents on the second day,
8 cents on the third day, and so forth)

8. Exponential Functions
x
bxf )(
base
Variable is in
exponent
*Just because a function has an exponent,
doesn’t mean it is an exponential function

9. xxxf 43)( 2

12
3)( 
 x
xg
13)( 3
 xxh
23)(  xth
12
23)( 
 x
xf

10. Basic Graphs
x
xf 2)( 

11. Basic Graphs
x
xf 






2
1
)(

12. This is
considered
Exponential
Growth

13. What
common point
do they all
pass through?

14. This is
considered
Exponential
Decay

16. Exponential Functions with Initial
Values
x
baxf )(
Initial Value,
or initial
population
Rate of
growth or
decay
Some unit of
time (usually)

17. Exponential Functions with Initial
Values
Initial Value,
or initial
population
Rate of
growth or
decay
Some unit of
time (usually)
t
rPtP 0)( 

18. …Quick Algebra Check!...
 2
23
   
3
2
1
4

19. A bacteria starts with an initial count of 3000
and doubles every hour.
How many bacteria after 3.5 hours?
When will there be 25,000 bacteria?

20. A bacteria starts with an initial count of 3000.
An antibiotic is introduced, causing half of the
bacteria to die off each hour.
How many bacteria after 3.5 hours?
When will there be 500 bacteria?

21. Finding Exponential Functions
Need initial value (0, …), and another
data point (x, y).
Substitute into exponential function:
Solve for the growth/decay rate.
Then rewrite exp. function.
(similar to what we’ve done before)
x
baxf )(

22. Finding Exponential Functions
Find the exponential function of the
form that passes through the points
(0,100) and (4, 1600)
x
baxf )(

23. Finding Exponential Functions
A population of bacteria grew from 24
to 615 over the course of 5 hours, find
an exponential function to model this
growth x
baxf )(

24. Finding Exponential Functions
x
baxf )(
The table shows
consumer credit (billions)
for various years.
Find an exponential
function and estimate
credit for the year 2016

25. Classwork
• Page 220
1 – 6 All
19, 20 – 30 all,
45, 49