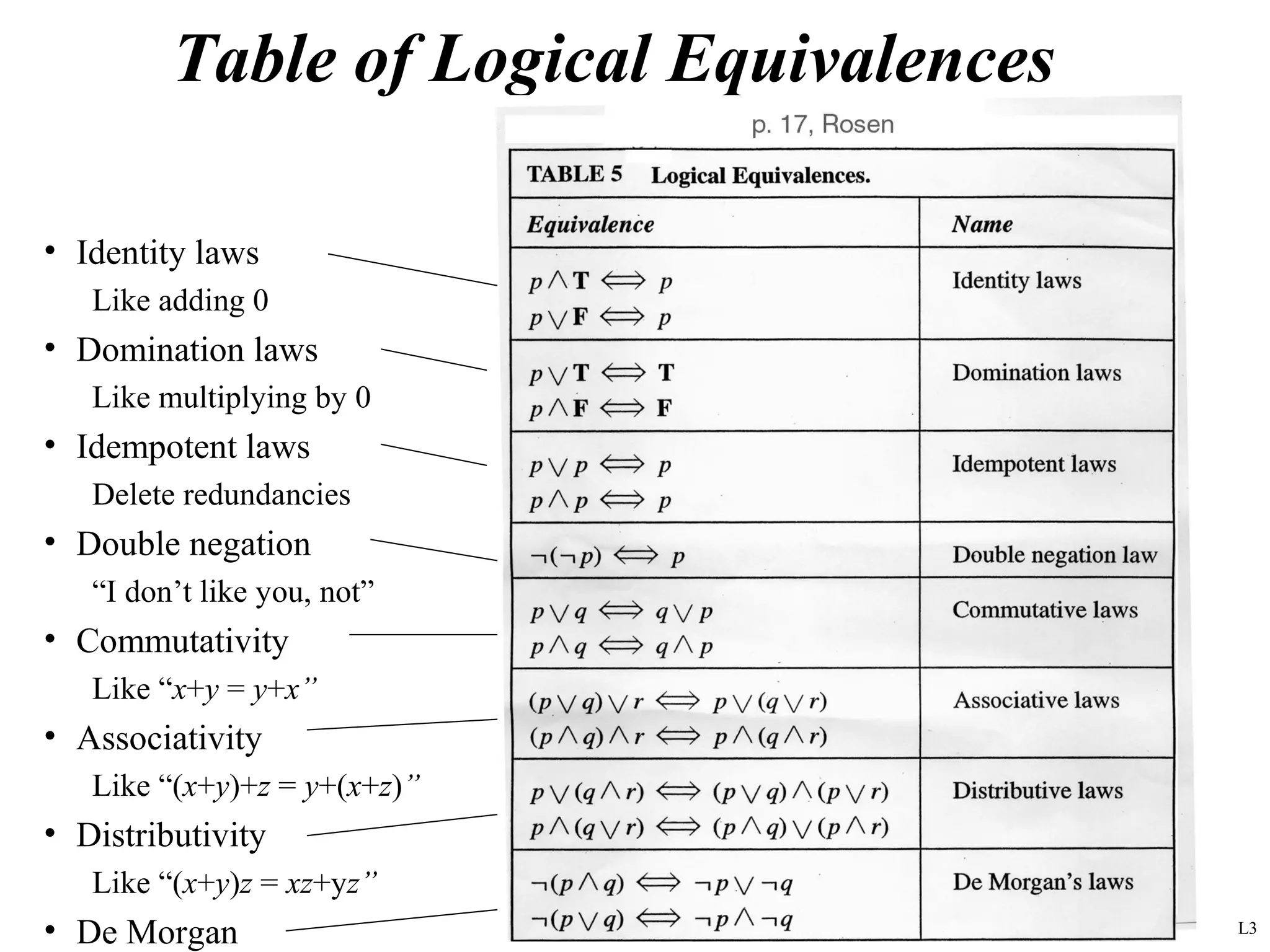
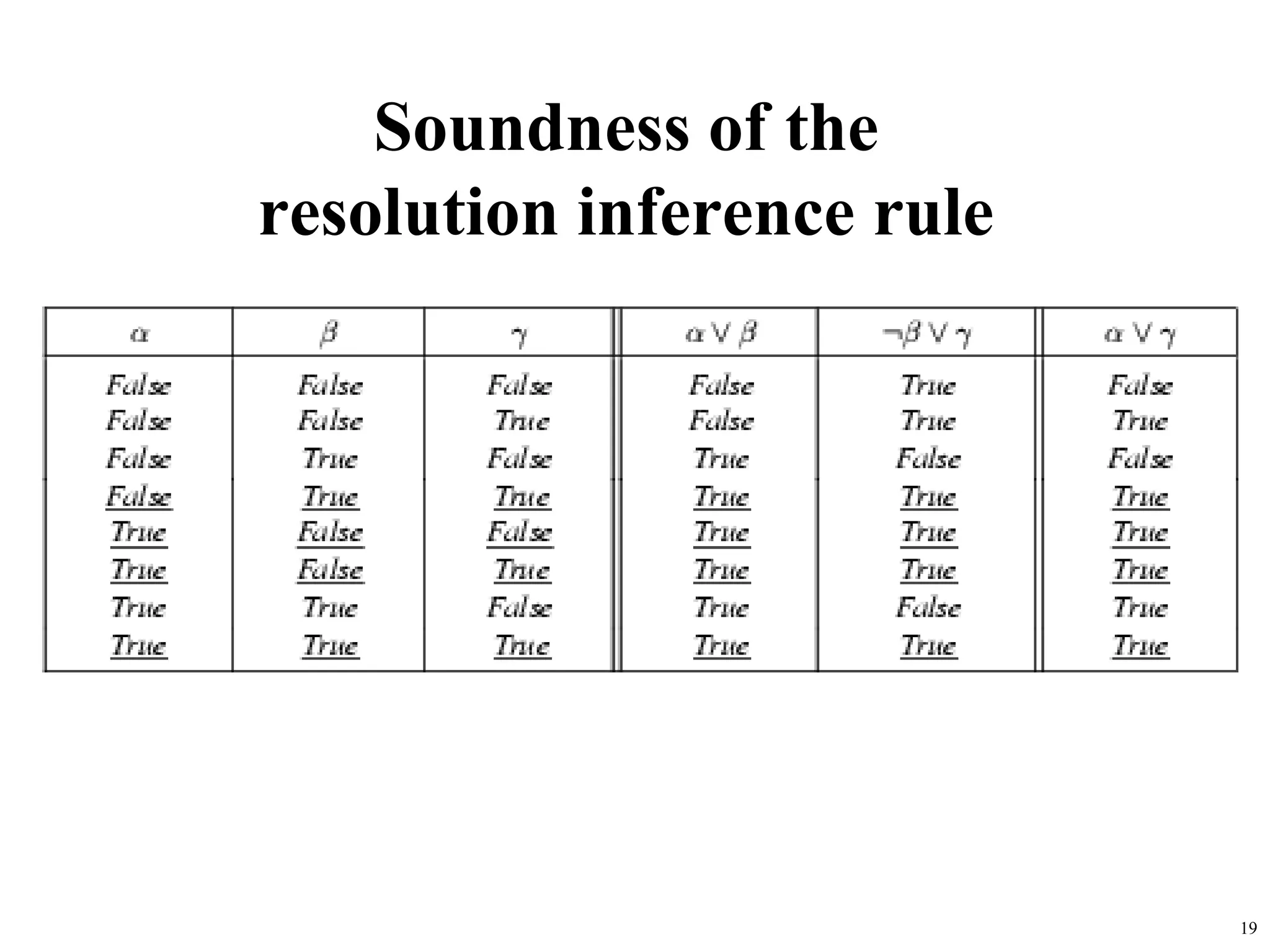
This document provides an introduction to propositional logic and first-order logic. It defines propositional logic, including propositional variables, connectives like conjunction and disjunction, and the laws of propositional logic. It then introduces first-order logic, which adds quantifiers, variables, functions, and predicates to represent objects, properties, and relations in a domain. First-order logic allows for more expressive statements about individuals and generalizations than propositional logic alone.

1. Propositional and
First-Order Logic
1

2. Propositional Logic
2

3. Propositional logic
• Proposition : A proposition is classified as a declarative
sentence which is either true or false.
eg: 1) It rained yesterday.
• Propositional symbols/variables: P, Q, S, ... (atomic
sentences)
• Sentences are combined by Connectives:
∧ ...and [conjunction]
∨ ...or [disjunction]
⇒ ...implies [implication / conditional]
⇔ ..is equivalent [biconditional]
¬ ...not [negation]
• Literal: atomic sentence or negated atomic sentence
3

4. Propositional logic (PL)
Sentence or well formed formula
• A sentence (well formed formula) is defined as follows:
– A symbol is a sentence
– If S is a sentence, then ¬S is a sentence
– If S is a sentence, then (S) is a sentence
– If S and T are sentences, then (S ∨ T), (S ∧ T), (S → T), and (S ↔ T) are
sentences
– A sentence results from a finite number of applications of the above rules
5

5. Laws of Algebra of Propositions
• Idempotent:
pVp≡p pΛp≡p
• Commutative:
pVq≡qVp pΛq≡qΛp
• Complement:
p V ~p ≡ T p Λ ~p ≡ F
• Double Negation:
~(~p) ≡ p
7

6. • Associative:
p V (q V r) ≡ (p V q) V r
p Λ (q Λ r) ≡ (p Λ q) Λ r
• Distributive:
p V (q Λ r) ≡ (p V q) Λ (p V r)
p Λ (q V r) ≡ (p Λ q) V (p Λ r)
• Absorbtion:
p V (p Λ q) ≡ p
p Λ (p V q) ≡ p
• Identity:
pVT≡T pΛT≡p
pVF≡p pΛF≡F 8

7. • De Morgan’s
~(p V q) ≡ ~p Λ ~q
~(p Λ q) ≡ ~p V ~q
• Equivalence of Contrapositive:
p → q ≡ ~q → ~p
• Others:
p → q ≡ ~p V q
p ↔ q ≡ (p → q) Λ (q → p)
9

8. Tautologies and contradictions
• A tautology is a sentence that is True under all
interpretations.
• An contradiction is a sentence that is False under all
interpretations.
p ¬p p ∨¬p p ¬p p ∧¬p
F T T F T F
T F T T F F
10
L3

9. Tautology by truth table
p q ¬p p ∨q ¬p ∧(p ∨q ) [¬p ∧(p ∨q )]→q
T T F T F T
T F F T F T
F T T T T T
F F T F F T
11
L3

10. Propositional Logic - one last proof
Show that [p ∧ (p → q)] → q is a tautology.
We use ≡ to show that [p ∧ (p → q)] → q ≡ T.
[p ∧ (p → q)] → q
≡ [p ∧ (¬p ∨ q)] → q substitution for →
≡ [(p ∧ ¬p) ∨ (p ∧ q)] → q distributive
≡ [ F ∨ (p ∧ q)] → q complement
≡ (p ∧ q) → q identity
≡ ¬(p ∧ q) ∨ q substitution for →
≡ (¬p ∨ ¬q) ∨ q DeMorgan’s
≡ ¬p ∨ (¬q ∨ q ) associative
≡ ¬p ∨ T complement
≡T identity
11/09/12
12

11. Logical Equivalence of
Conditional and Contrapositive
The easiest way to check for logical equivalence is to
see if the truth tables of both variants have
identical last columns:
p q p →q p q ¬q ¬p ¬q→¬p
T T T T T F F T
T F F T F T F F
F T T F T F T T
F F T F F T T T
13
L3

12. Table of Logical Equivalences
• Identity laws
Like adding 0
• Domination laws
Like multiplying by 0
• Idempotent laws
Delete redundancies
• Double negation
“I don’t like you, not”
• Commutativity
Like “x+y = y+x”
• Associativity
Like “(x+y)+z = y+(x+z)”
• Distributivity
Like “(x+y)z = xz+yz” 14
• De Morgan L3

13. Table of Logical Equivalences
• Excluded middle
• Negating creates opposite
• Definition of implication in terms
of Not and Or
15
L3

14. Inference rules
• Logical inference is used to create new sentences that
logically follow from a given set of predicate calculus
sentences (KB).
16

15. Sound rules of inference
• Here are some examples of sound rules of inference
– A rule is sound if its conclusion is true whenever the premise is true
• Each can be shown to be sound using a truth table
RULE PREMISE CONCLUSION
Modus Ponens A, A → B B
And Introduction/Conjuction A, B A∧B
And Elimination/SimplificationA ∧ B A
Double Negation ¬¬A A
Unit Resolution A ∨ B, ¬B A
Resolution A ∨ B, ¬B ∨ C A∨ C
17

16. Soundness of modus ponens
A B A→B OK?
True True True
√
True False False
√
False True True
√
False False True
√
18

17. Soundness of the
resolution inference rule
19

18. Proving things
• A proof is a sequence of sentences, where each sentence is either a
premise or a sentence derived from earlier sentences in the proof
by one of the rules of inference.
• The last sentence is the theorem (also called goal or query) that
we want to prove.
• Example for the “weather problem” given above.
1 Hu Premise “It is humid”
2 Hu→Ho Premise “If it is humid, it is hot”
3 Ho Modus Ponens(1,2) “It is hot”
4 (Ho∧Hu)→R Premise “If it’s hot & humid, it’s raining”
5 Ho∧Hu And Introduction(1,3) “It is hot and humid”
6R Modus Ponens(4,5) “It is raining”
20

19. Problems with Propositional Logic
21

20. Propositional logic is a weak language
• Hard to identify “individuals” (e.g., Mary, 3)
• Can’t directly talk about properties of individuals or
relations between individuals (e.g., “Bill is tall”)
• Generalizations, patterns, regularities can’t easily be
represented (e.g., “all triangles have 3 sides”)
• First-Order Logic (abbreviated FOL or FOPC) is expressive
enough to concisely represent this kind of information
FOL adds relations, variables, and quantifiers, e.g.,
• “Every elephant is gray”: ∀ x (elephant(x) → gray(x))
• “There is a white alligator”: ∃ x (alligator(X) ^ white(X))
22

21. First-Order Logic
23

22. First-order logic
• First-order logic (FOL) models the world in terms of
– Objects, which are things with individual identities
– Properties of objects that distinguish them from other objects
– Relations that hold among sets of objects
– Functions, which are a subset of relations where there is only one
“value” for any given “input”
• Examples:
– Objects: Students, lectures, companies, cars ...
– Relations: Brother-of, bigger-than, outside, part-of, has-color,
occurs-after, owns, visits, precedes, ...
– Properties: blue, oval, even, large, ...
– Functions: father-of, best-friend, second-half, one-more-than ...
24

23. User provides
• Constant symbols, which represent individuals in the world
– Mary
–3
– Green
• Function symbols, which map individuals to individuals
– father-of(Mary) = John
– color-of(Sky) = Blue
• Predicate symbols, which map individuals to truth values
– greater(5,3)
– green(Grass)
– color(Grass, Green)
25

24. FOL Provides
• Variable symbols
– E.g., x, y, foo
• Connectives
– Same as in PL: not (¬), and (∧), or (∨), implies (→), if
and only if (biconditional ↔)
• Quantifiers
– Universal ∀x or (Ax)
– Existential ∃x or (Ex)
26

25. Quantifiers
• Universal quantification
– (∀x)P(x) means that P holds for all values of x in the
domain associated with that variable
– E.g., (∀x) dolphin(x) → mammal(x)
• Existential quantification
– (∃ x)P(x) means that P holds for some value of x in the
domain associated with that variable
– E.g., (∃ x) mammal(x) ∧ lays-eggs(x)
– Permits one to make a statement about some object
without naming it
27

26. Quantifiers
• Universal quantifiers are often used with “implies” to form “rules”:
(∀x) student(x) → smart(x) means “All students are smart”
• Universal quantification is rarely used to make blanket statements
about every individual in the world:
(∀x)student(x)∧smart(x) means “Everyone in the world is a student and is smart”
• Existential quantifiers are usually used with “and” to specify a list of
properties about an individual:
(∃x) student(x) ∧ smart(x) means “There is a student who is smart”
• A common mistake is to represent this English sentence as the FOL
sentence:
(∃x) student(x) → smart(x)
– But what happens when there is a person who is not a student?
28

27. Quantifier Scope
• Switching the order of universal quantifiers does not change
the meaning:
– (∀x)(∀y)P(x,y) ↔ (∀y)(∀x) P(x,y)
• Similarly, you can switch the order of existential
quantifiers:
– (∃x)(∃y)P(x,y) ↔ (∃y)(∃x) P(x,y)
• Switching the order of universals and existentials does
change meaning:
– Everyone likes someone: (∀x)(∃y) likes(x,y)
– Someone is liked by everyone: (∃y)(∀x) likes(x,y)
29

28. Connections between All and Exists
We can relate sentences involving ∀ and ∃
using De Morgan’s laws:
(∀x) ¬P(x) ↔ ¬(∃x) P(x)
¬(∀x) P ↔ (∃x) ¬P(x)
(∀x) P(x) ↔ ¬ (∃x) ¬P(x)
(∃x) P(x) ↔ ¬(∀x) ¬P(x)
30

29. Quantified inference rules
• Universal instantiation
∀x P(x) ∴ P(A)
• Universal generalization
– P(A) ∧ P(B) … ∴ ∀x P(x)
• Existential instantiation
∃x P(x) ∴P(F)
• Existential generalization
– P(A) ∴ ∃x P(x)
31

30. Universal instantiation
(a.k.a. universal elimination)
• If (∀x) P(x) is true, then P(C) is true, where C is any
constant in the domain of x
• Example:
(∀x) eats(Ziggy, x) ⇒ eats(Ziggy, IceCream)
32

31. Translating English to FOL
Every gardener likes the sun.
∀x gardener(x) → likes(x,Sun)
You can fool some of the people all of the time.
∃x ∀t person(x) ∧time(t) → can-fool(x,t)
You can fool all of the people some of the time.
∀x ∃t (person(x) → time(t) ∧can-fool(x,t))
Equivalent
∀x (person(x) → ∃t (time(t) ∧can-fool(x,t))
All purple mushrooms are poisonous.
∀x (mushroom(x) ∧ purple(x)) → poisonous(x)
No purple mushroom is poisonous.
¬∃x purple(x) ∧ mushroom(x) ∧ poisonous(x)
∀x (mushroom(x) ∧ purple(x)) → ¬poisonous(x) Equivalent
Clinton is not tall.
¬tall(Clinton)
33

32. 34