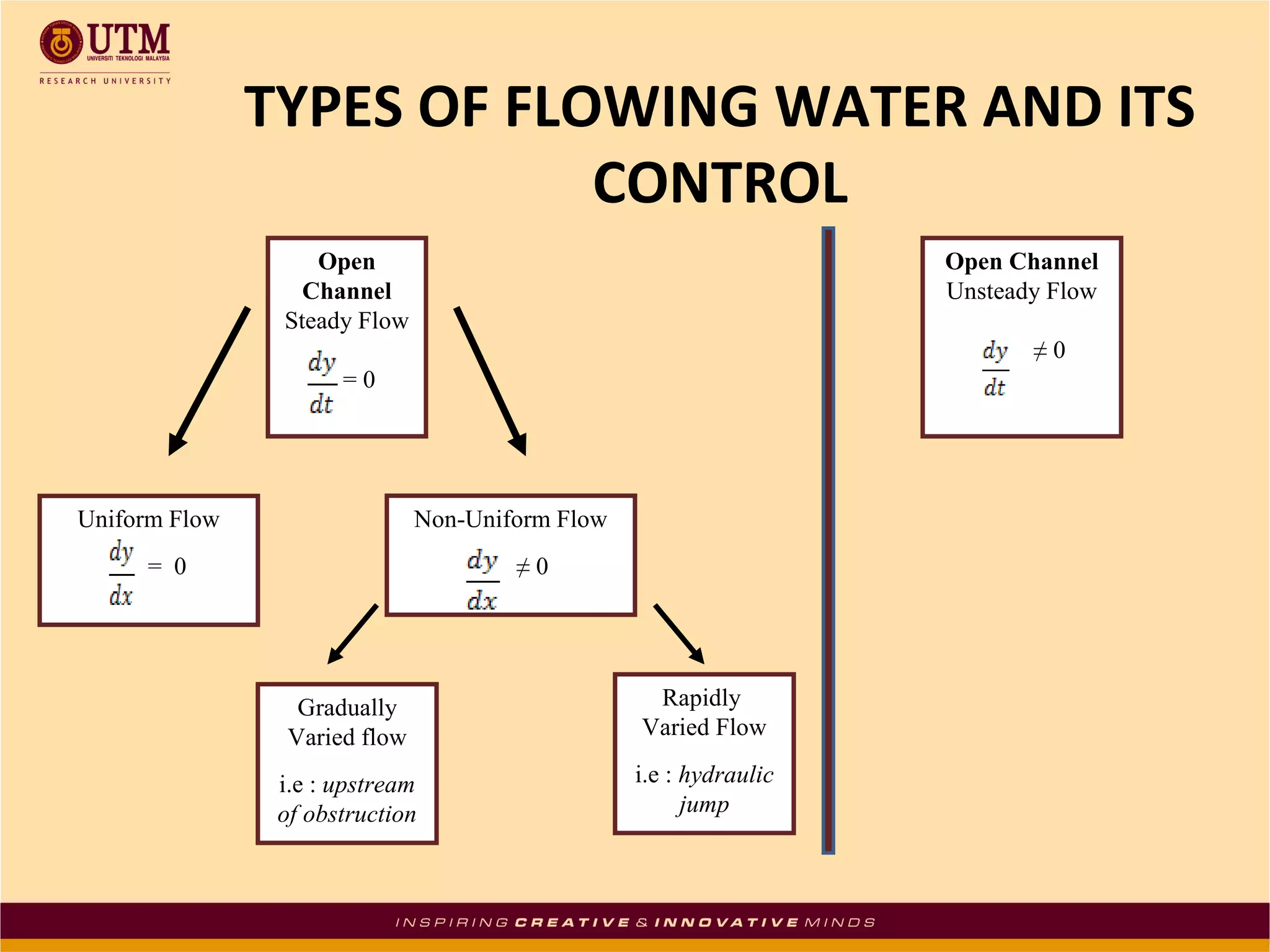
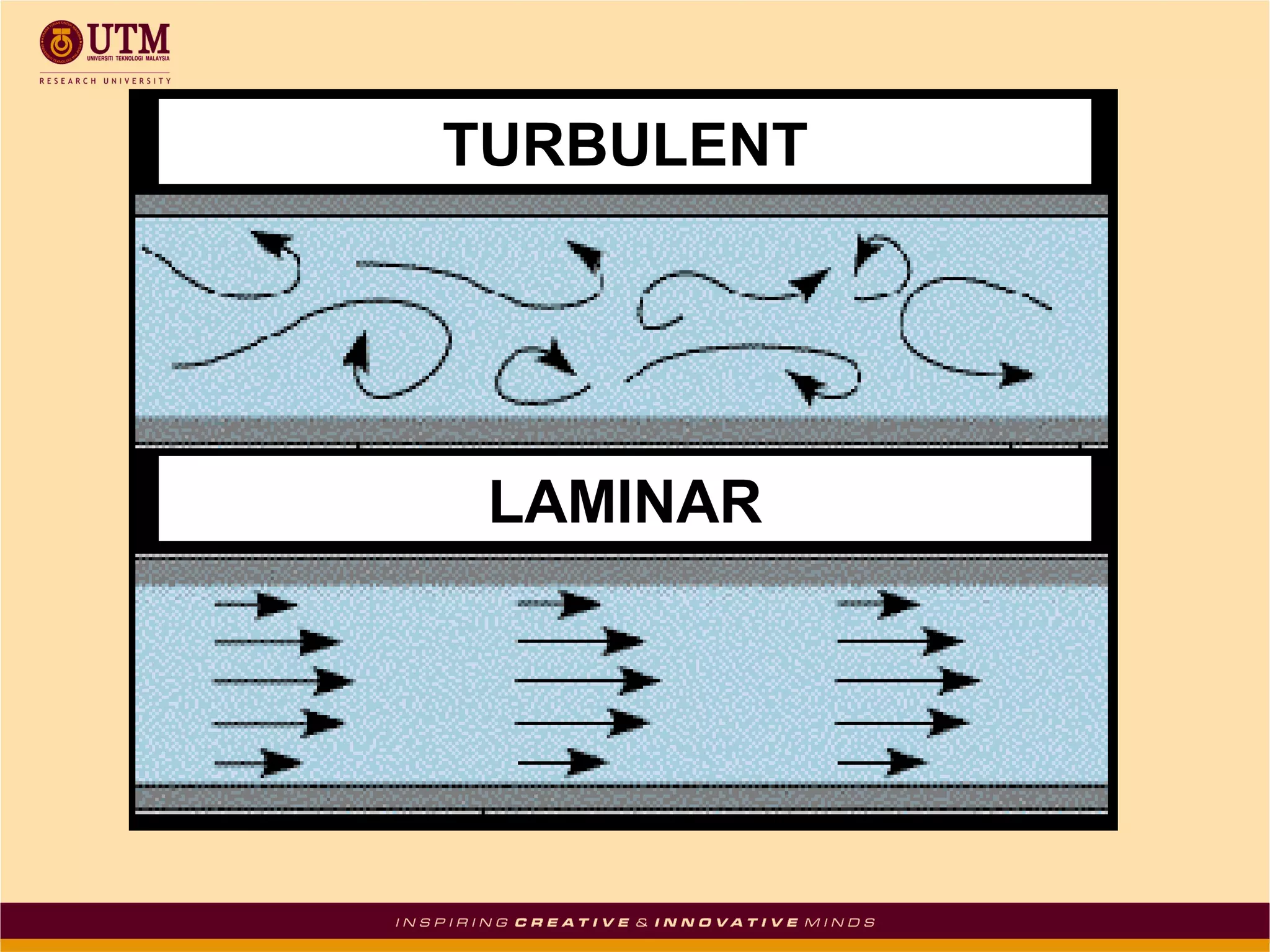
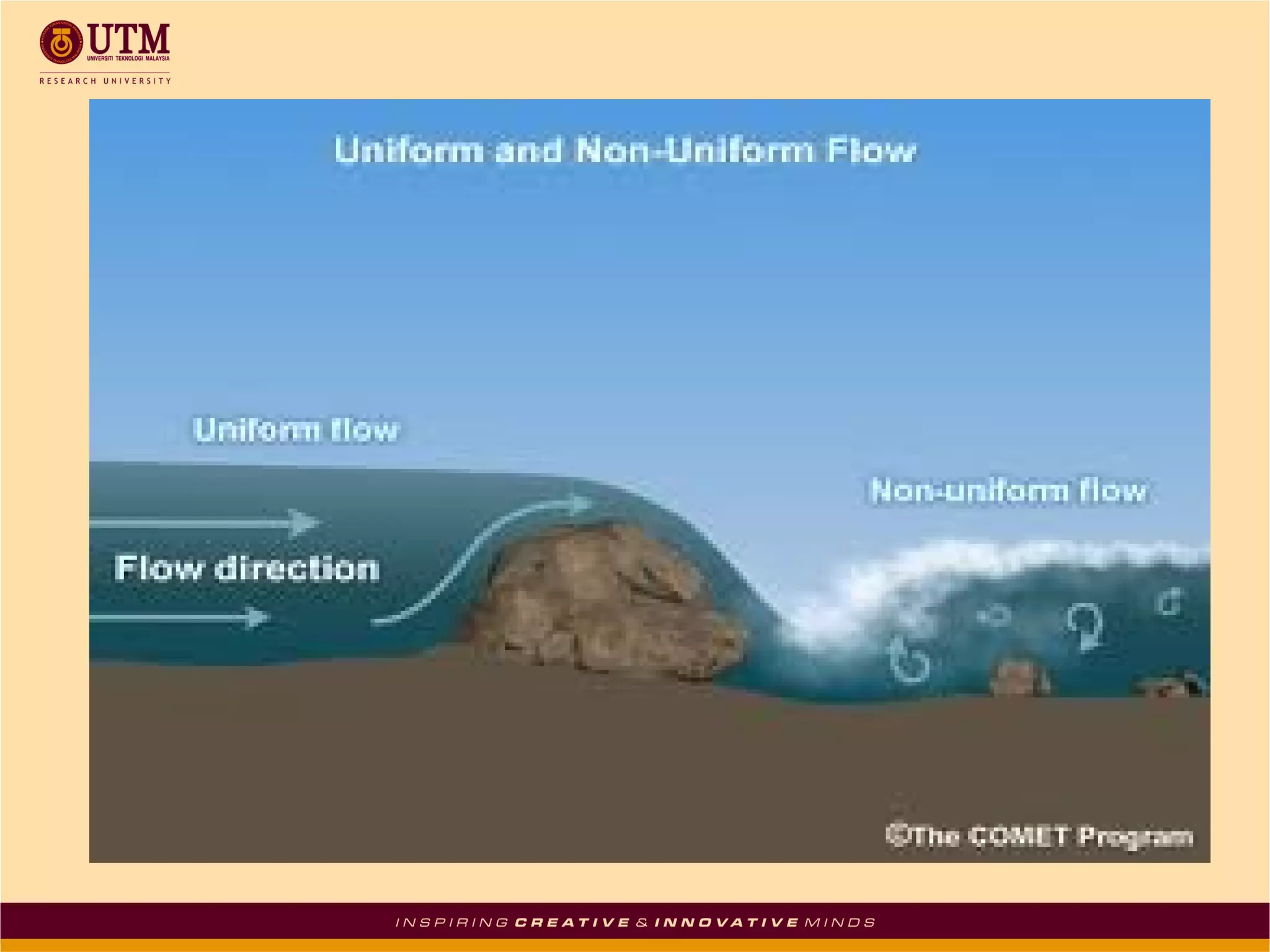
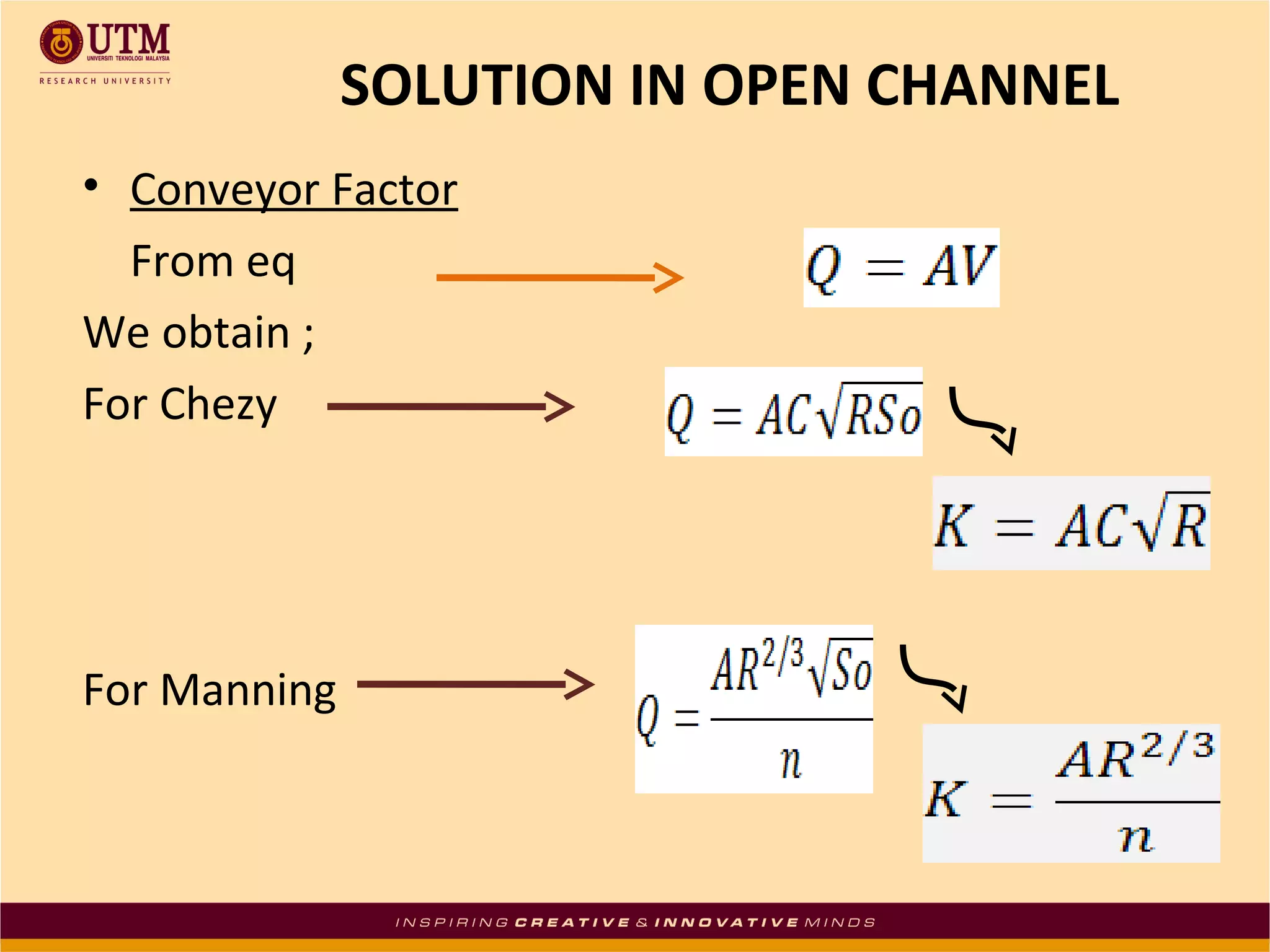
This document summarizes uniform flow in open channels. It defines open channels as streams not completely enclosed by boundaries with a free water surface. Open channels can be natural or artificial with regular shapes. Uniform flow occurs when the depth, area, velocity and discharge remain constant in a channel with a constant slope and roughness. The Chezy and Manning formulas are presented to calculate mean flow velocity from hydraulic radius, slope and conveyance factors. Examples are given to solve for velocity, flow rate, and channel slope using the formulas.

1. HYDRAULICS ENGINEERING
UNIFORM FLOW IN OPEN CHANNELS
By
Erni Syuhada Bt Mazwil Ishan

2. HYDRAULICS ENGINEERING
• A scientific fluid flow particularly in water
thoroughly in pipe, open channel, orifice and
embankment, including the problem related
to energy and pressure.
• Related to water or fluid in dynamic condition.

3. CONTENT
 What is Open Channel
 Types of Open Channel
 Types of flowing water and control
 Solution of uniform flow in Open Channel

4. OPEN CHANNEL
An open channel :
a)The stream not completely enclosed by solid
boundaries
b)It has free surface subjected only to
atmospheric pressure.
c) Referred as free-surface flow or gravity flow

5. TYPES OF OPEN CHANNEL
Open Channel
Natural Channel
Irregular shape
Artificial Channel
Regular shape
i.e : river, hillsides
rivulets, tidal etuaries
i.e : drains, culverts,
sewer, tunnels

6. TYPES OF OPEN CHANNEL

7. TYPES OF FLOWING WATER AND ITS
CONTROL
Open
Channel
Steady Flow
Open Channel
Unsteady Flow
≠0
=0
Uniform Flow
Non-Uniform Flow
= 0
≠0
Gradually
Varied flow
Rapidly
Varied Flow
i.e : upstream
of obstruction
i.e : hydraulic
jump

8. TYPES OF FLOWING WATER AND ITS
CONTROL
Steady
• y (depth of water) and v (velocity) remain constant
with respect to time
Unsteady Flow
• y and v change with time

9. TYPES OF FLOWING WATER AND ITS
CONTROL
Uniform
• y (depth of water) and v (velocity) remain constant
along the channel. Figure 2.0
Figure 2.0
Non - uniform Flow
• y and v change along the length of the
channel

10. TYPES OF FLOWING WATER AND ITS
CONTROL
• Flow Classifications
1) Depending on the Reynolds number, Re
– Laminar Flow (if Re < 500): very slow and shallow
flowing water in very smooth open channels.
– Turbulent Flow (if Re > 1000): ordinary flow in
ordinary open channels.
– Transition Flow (if 500 < Re < 1000)
V = average channel velocity
L = length of channel
v = kinematic viscosity of fluid

11. TYPES OF FLOWING WATER AND ITS
CONTROL
2) Depending on Froude number, Fr
– Fr = 1 : Critical Flow
– Fr < 1 : Subcritical Flow – slow flowing water
– Fr > 1 : Supercritical Flow – fast flowing water
V = average channel velocity
g = gravity acceralation
D = hydraulics water depth

12. TURBULENT
LAMINAR

15. TYPES OF FLOWING WATER AND ITS
CONTROL
Critical Section (In uniform and non-uniform flow)
1) If So < Sc, y > yc : Subcritical flow
2) If So = Sc, y = yc : Critical flow
3) If So > Sc, y < yc : Supercritical flow
Figure 3.0

16. Bernoulli’s Equation
2
2
p1 V1
p2 V2
+
+ z1 =
+
+ z 2 + hL
γ 2g
γ
2g

17. GEOMETRIC PROPERTIES OF OPEN
CHANNELS
Open Channel
RECTANGULAR CHANNEL
TRAPEZOIDAL CHANNEL

18. GEOMETRIC PROPERTIES OF OPEN
CHANNELS
• The terminology of geometric elements
y : depth of flow
m : side slope
T : top width
So : channel bottom slope
b : bottom channel width
v : average flow density
Fr : Froude number
Q : flow rates , Q = AV
R: hydraulic radius at cross
section
ν : velocity
θ : flow temperature
Re : Reynold number
L : length of channel
A : area of the flow
P : wetted perimeter
D : hydraulics water depth V : volume
E : specific energy
∆z : weir height
q = discharge over width
(m)

19. GEOMETRIC PROPERTIES OF OPEN
CHANNELS
Type of
TOP WIDTH,
channel
T
RECTANGULAR
B
AREA, A
By
WETTED
PERIMETER, P
B + 2y
TRAPEZOIDAL
By + my2
B+2y √ 1+m2
Where,
B+2my

20. UNIFORM FLOW IN OPEN CHANNEL
Uniform flow is an equilibrium condition that flow
tends to if the channel :
a)constant slope
b)constant cross section
c)constant roughness
d)depth, water area, velocity and discharge at every
section of channel are constant
e)channel bed, water surface and energy line are
parallel, So = Sw = S
f)y1 = y2 , V1 = V2

21. UNIFORM FLOW IN OPEN CHANNEL
• CHEZY FORMULA :
Where ; V = mean velocity (m/s)
C = Chezy’s factor of flow resistance (m1/2/s)
R = hydraulic radius
So = slope of energy line
Q = Discharge (m3/s)
• MANNING FORMULA :
Where ; V = mean velocity (m/s)
n = Manning’s coefficient of roughness (s/m1/3)
R = hydraulic radius
So = slope of energy line
Q = Discharge (m3/s)

22. UNIFORM FLOW IN OPEN CHANNEL
Typical values of Manning’s coefficient, n
Closed conduits flowing partly full
Corrugated metal storm drains
Concrete culvert
Unfinished concrete
Clay drain tile
Lined or built up channels
Unpainted steel
Planed wood
Unplaned wood
Trowel – finished concrete
Rough concrete
Glazed brick
Brick in cement mortar
Excavated channels
Clean earth (straight channel)
Earth with weeds (winding channel)
Natural streams
Clean and straight
Weedy reaches, deep pools
0.010
0.024
0.013
0.014
0.012
0.012
0.013
0.013
0.017
0.020
0.013
0.022
0.030
0.030
0.100

23. SOLUTION IN OPEN CHANNEL
• Conveyor Factor
From eq
We obtain ;
For Chezy
For Manning

24. SOLUTION IN OPEN CHANNEL
• Section Factor, Z
For Chezy ;
For Manning;
• Thus, normal depth, yo can be obtain by using
trial and error method

25. SOLUTION IN OPEN CHANNEL
• Example :
Given trapezoidal channel 10m wide with side
slope of 1:1.5. Bed slope is 0.0003. The
channel with concrete lining, n = 0.012.
Calculate the velocity, V and flow rate, Q
when the flow depth is 3.0m. If the flow rate
is 50m/s, determine the slope, So of channel.