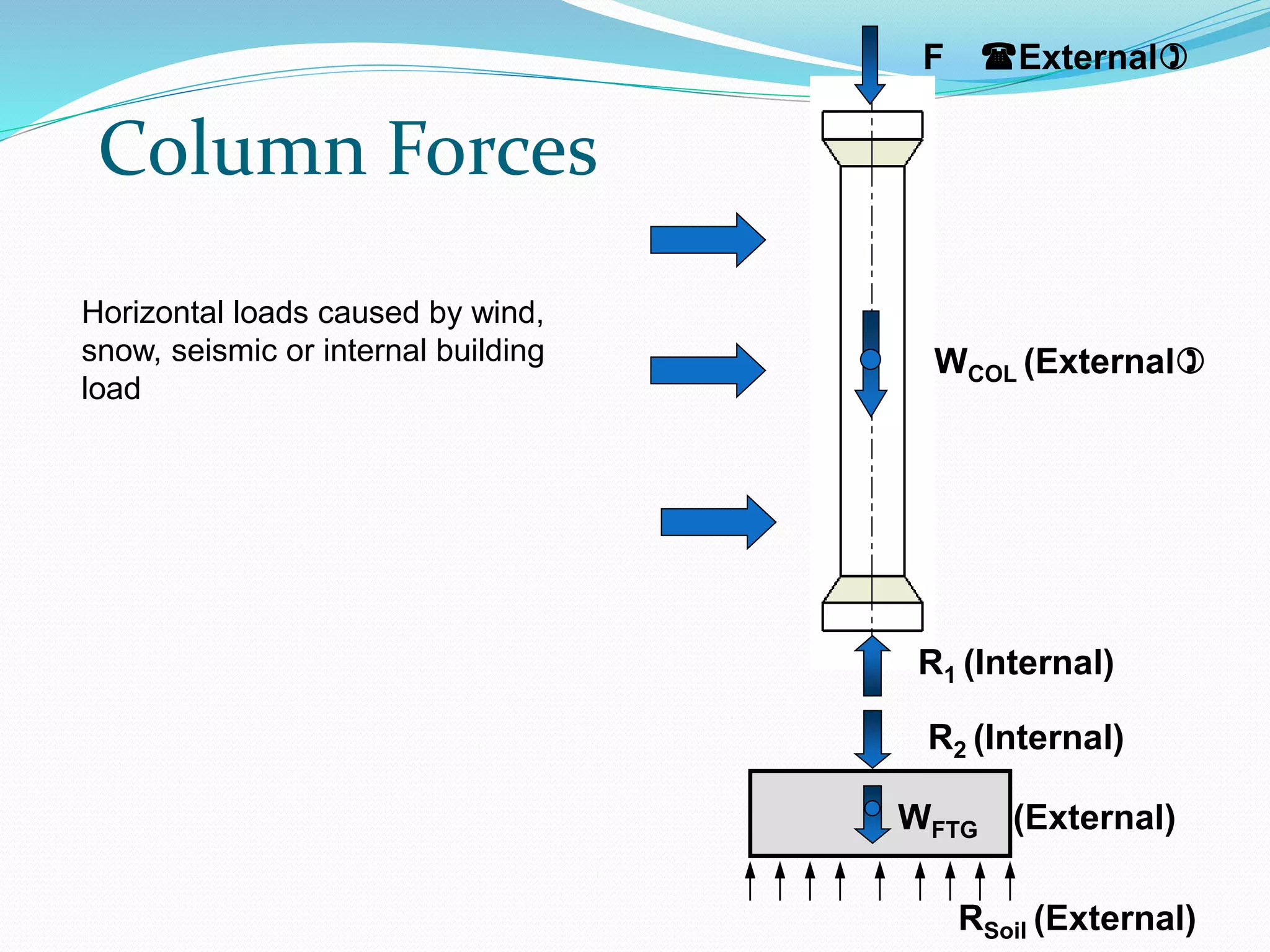
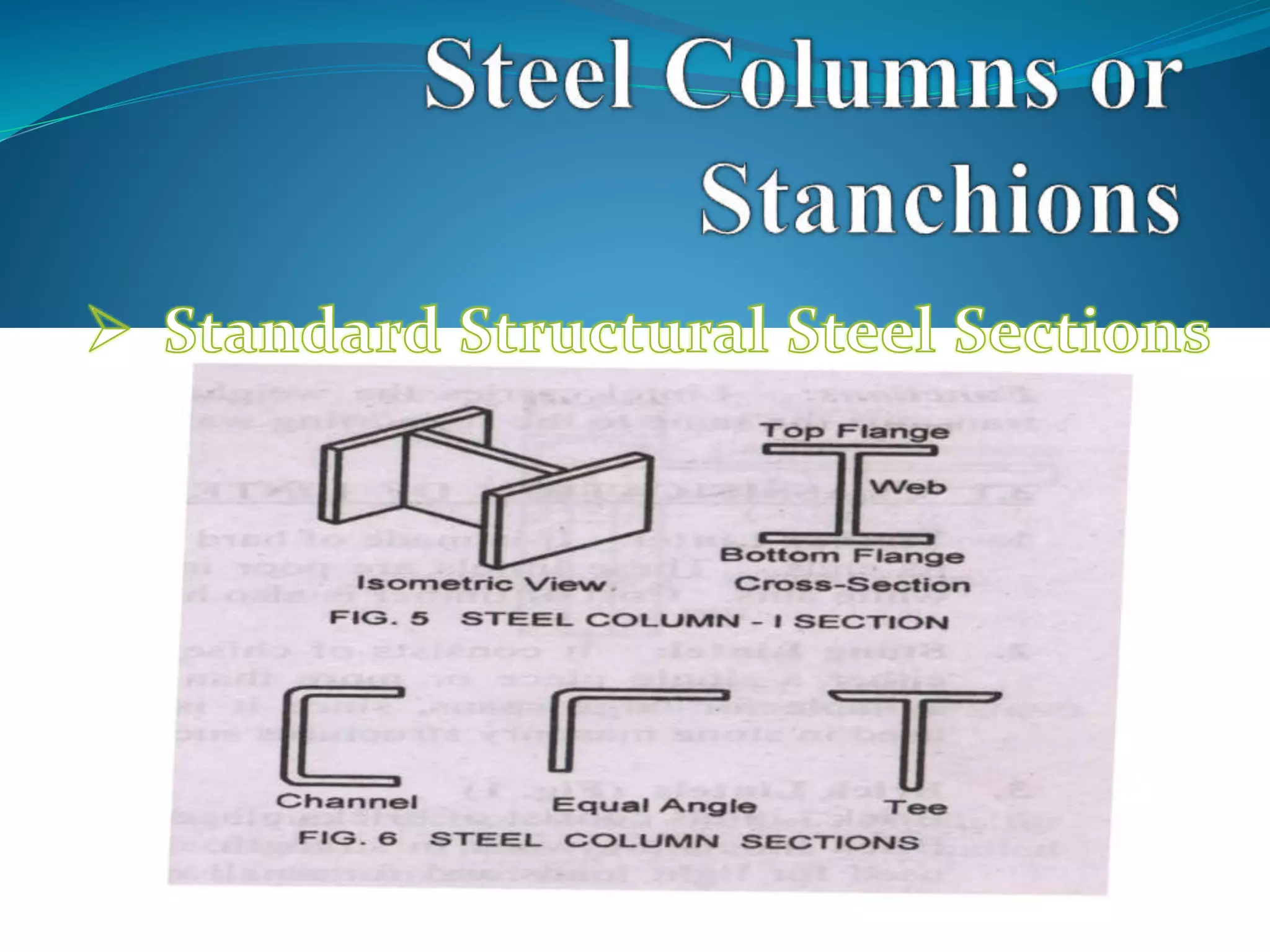
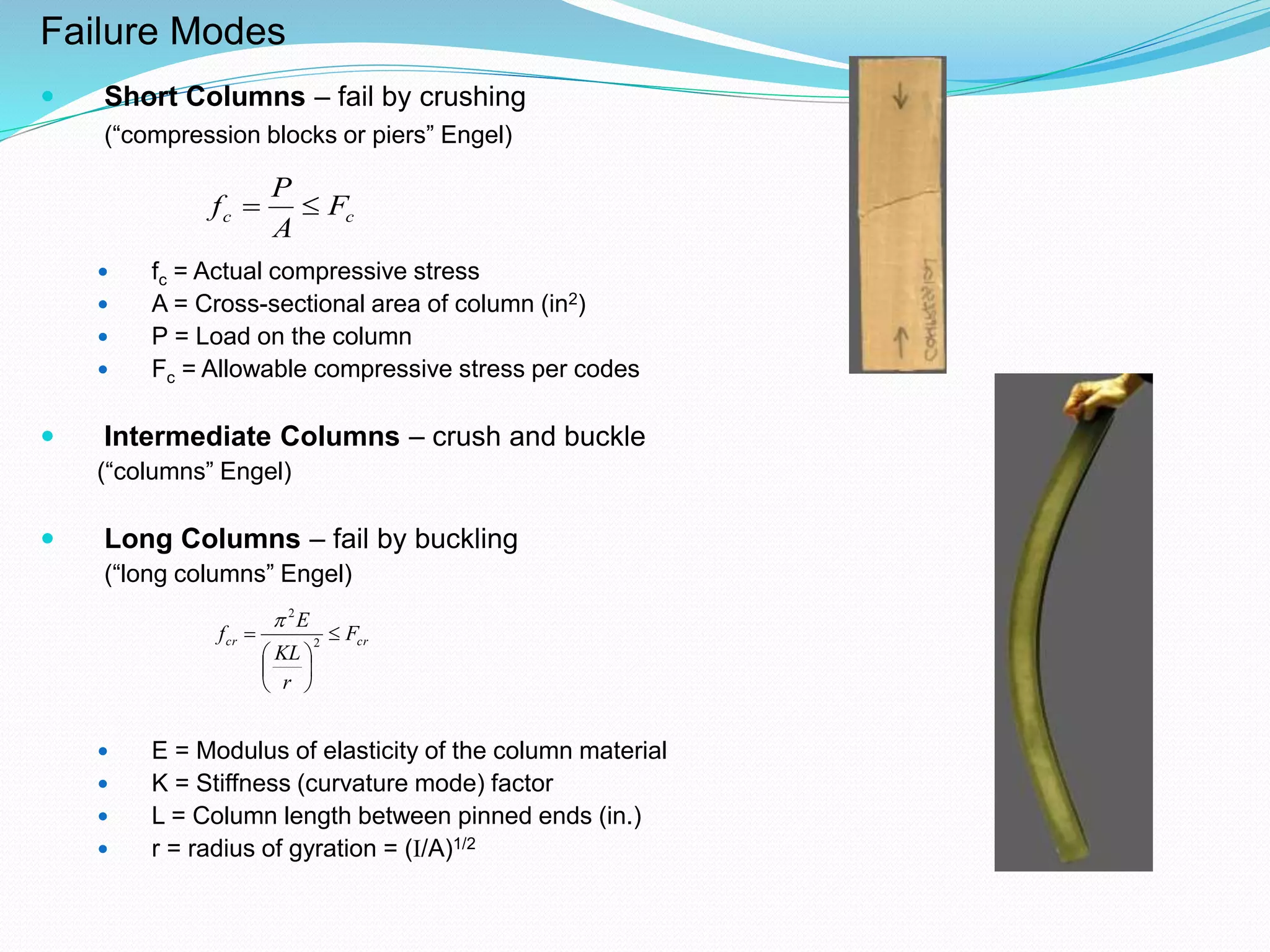
1. The document discusses reinforcement in concrete columns. It lists group members for a project and provides information on different types of columns, their load transfer mechanisms, and failure modes. 2. Key points covered include defining short, long, and intermediate columns based on their slenderness ratio. It also discusses calculating the effective length and radius of gyration of a column. 3. The document provides guidelines for steel reinforcement in columns, including minimum bar diameter and concrete cover, as well as the design procedure and considerations for selecting the reinforcement ratio.

2. Group members
1-M. Ismail Joiya
2- M.Adnan doger
3-M.Asif
4-Tariq Rasool
5-Sajjad Ahmad
6-Irfan Hussan

3. WHAT IS COLUMN?
 Column is a vertical structural member. It
transmits the load from ceiling/roof slab
and beam, including its self-weight to the
foundation. Columns may be subjected to
a pure compressive load. R.C.C. columns
are the most widely used now-a-days.

4. Columns
 Columns carry primary Axial Loads and therefore are
designed for compression.
 Additional loads from snow, wind or other horizontal
forces can cause bending in the columns.
 Columns then need to be designed for Axial Load and
Bending.

5. Columns
 Longitudinal rebar runs
vertically and is held in
place by ties
 Longitudinal bars are
typically about 4% of
the gross column area;
ties are usually #3 or #4
bars
 Typically designed for
compression, but must
be able to resist bending
Photo courtesy of John Gambatese

6. Column Forces
F (External)
WCOL (External)
R1 (Internal)
R2 (Internal)
RSoil (External)
WFTG (External)
Horizontal loads caused by wind,
snow, seismic or internal building
load

7. COLUMN LOAD TRANSFER FROM
BEAMS

8. Types Of Columns
 Long Columns
 Short (Strut) Columns
 Intermediate Columns

9. Long Column
When the ratio of effective length to the least radius of
gyration is greater than 45, then it is called a long column.
A long column is subjected to bending moment
in addition to direct compressive stress.
The load carrying capacity of a long column is less than a
short column
The load carrying capacity of a long column depends upon
slenderness ratio (slenderness ratio increases then the
capacity of the column decreases)

10.  LONG COLUMN :
 When length of column is more as compared to
its c/s dimension, it is called long column.
Long Column
Le/rmin > 50
Where,
Le = effective length of column
rmin = Minimum radius of gyration

11. Real world example:
 Here in picture we can see long columns on front of
building in “The White house” Washington D.C(USA).

12. Short Column:

When the ratio of effective length to the least lateral
dimensions of the column is less than 12, then it is
called a short column.
(or)
When the ratio of effective length to the least radius of
gyration is less than 45, then it is called a short column

13. SHORT COLUMN :
 When length of column is less as compared to its c/s
dimension, it is called Short column.
Short Column
Le/rmin <50
Or,
Le/d < 15
 Crushing Load : The load at which short column fails
by crushing is called crushing load.

14. INTERMEDIATE COLUMN:
 Column is intermediate when
4d < L < 30d
and
30 < Le /r min < 100 or Critical slenderness ratio.

15. What is the definition of the slenderness
ratio of a column?
 Slenderness ratio is the ratio of the length of a column
and the least radius of gyration of its cross section
 Often denoted by lambda
 λ = le/rmin

16. Uses of slenderness ratio
 It is used extensively for finding out the design load as
well as in classifying various columns in
short/intermediate/long
 Example-
Short Steel column - lambda is less than 50.
Intermediate - 50 -250
Long - 250 above.

17. Why this is important?
 Long columns under compression can fail via both
buckling (bending side ways) as well as crushing.
Various formulas to calculate such failure
characteristics extensively use the use of this ratio.

18. Radius of gyration
Radius of gyration is used to describe the distribution
of cross sectional area in a column around
its censorial axis. The radius of gyration is given by the
following formula.
 R.g= i/A
 Where I is the second moment of inertia. and A is the
total cross-sectional area.

19. Calculating the radius of gyration
 To calculate the radius of gyration for the cross-section of
the beam in the diagram, start with the values of I that
were calculated earlier.
 Ixx = 33.3 x 106 mm4
 Iyy = 2.08 x 106 mm4
 Refer to the diagram for the values of b and d that are used
in the calculation of A.
 A = Area of cross-section = 50 mm x 200 mm = 10,000 mm2
 Substitute I and A into the formula for r to give:
 This is the value of the radius of gyration about the x-x axis.

24. Footing
Column
Girder
Beam
Partial View of 2nd floor Framing
For Clarity the Ground Floor Slab, 2nd Floor Slab and Roof
Framing and Roof Deck are not shown

25. 3D View of Retail Building
Steel Framing and 1st Floor Slab Shown

27. Failure Modes of COLUMN
 Column may fail in one of three condition
 Compression failure of concrete or steel
reinforcement
 Buckling
 Combination of buckling and compression failure
 Compression failure is likely to occur with columns
which are short and stocky.
 Buckling is probable with column which are long and
slender

28. Failure modes of columns
Compression
failure Buckling

31. CRIPPLING LOAD OR BUCKLING
LOAD
 The load at which, long column starts buckling(bending) is
called buckling load or crippling load.
 Buckling of column depends upon the following factors.
1. Amount of load.
2. Length of column
3. End condition of column
4. C/s dimensions of column
5. Material of column.

32. Failure Modes
 Short Columns – fail by crushing
(“compression blocks or piers” Engel)
 fc = Actual compressive stress
 A = Cross-sectional area of column (in2)
 P = Load on the column
 Fc = Allowable compressive stress per codes
 Intermediate Columns – crush and buckle
(“columns” Engel)
 Long Columns – fail by buckling
(“long columns” Engel)
 E = Modulus of elasticity of the column material
 K = Stiffness (curvature mode) factor
 L = Column length between pinned ends (in.)
 r = radius of gyration = (I/A)1/2
cc F
A
P
f 
crcr F
r
KL
E
f 






 2
2


33. Find the Effective length
 1. Both ends pinned
Effective length = actual length x 1.0
 2. Both ends fixed
Effective length = actual length x 0.5
 3. One end pinned
other end fixed
Effective length = actual length x 0.7
 4. One end fixed other end completely free
Effective length = actual length x 2.0

34. (Le) for different support
conditions.

35. In order to select the correct column for a particular
application
 Determine the effective length of the column required
 Select a trial section
 Using the radius of gyration value for this trial section
calculate the slenderness ratio.
 If the slenderness ratio is greater than 180, try a larger
cross section trial section.
 Using the slenderness ratio obtain the compressive
strength from tables. (from the Y-Y axis)

36. A column, pin ended, length 5m has an axial load of
1500kN. The steel has a yield stress of about 265MPa
Effective L = 1 x 5 = 5m
Choose a trial section – 203 x 203 / 86
From table 1 - Rad. Of Gyration = 5.32
SR = 5 / 0.0532(Needs to be in metre) = 94

37. Serial size
(mm)
Mass per unit
length (kg/m)
Area of
section (cm2)
Min Rad of
Gyration (cm)
305 x 305 283 360.4 8.25
198 252.3 8.02
137 174.6 7.82
97 123.3 7.68
254 x 254 167 212.4 6.79
107 136.6 6.57
89 114.0 6.52
73 92.9 6.46
203 x 203 86 110.1 5.32
71 91.1 5.28
60 75.8 5.19
52 66.4 5.16
46 58.8 5.11

38. Extract from Table 2
Axis of Buckling – Y – Y
Yield (MPa)
SR = 94
Comp
Strength
= 200MPa
(Approx)
SRatio
265 275 340
25 258 267 328
50 221 228 275
75 187 192 221
100 138 141 153
150 74 74 77

39. From Table 2 –
Compressive strength is approx 150MPa
The actual stress (s)
= Load / CSA
= 1500 x 103 / 110.1 x 10-4
= 132 MPa
This value is 18MPa below the required stress value
for this section
We should now repeat the process until we have a
stress value JUST below the 150 MPA value
TRY IT YOURSELF

40. WHAT IS UNIAXIALLY LOADED
COLUMN?
WHEN A COLUMN IS SUBJECTED
TO EITHER COMBINED AXIAL
COMPRESSION (P) AND
MOMENT (M) AS IN FIG-1 OR
ONLY AXIAL LOAD (P) APPLIED
AT AN ECENTRICITY e=(M/P) AS
IN FIG-2 SO THAT THE COLUMN
IS TRYING TO BEND ABOUT
ONLY ONE AXES OF THE
COLUMN CROSS SECTION IS
KNOWN AS UNIAXIALLY
LOADED COLUMN.

41. CROSS SECTION OF UNIAXIALLY
LOADED COLUMN

42. IN THIS CASE,COLUMNS
ARE SUBJECT TO
TENSION OVER A PART
OF THE SECTION AND
IF OVERLOADED MAY
FAIL DUE TO TENSILE
YIELDING OF THE
STEEL ON THE SIDE
FARTHEST FROM THE
LOAD.

43. 43
Steel Reinforcement in Columns
 The limiting steel ratio ranges between 1 % to 8 %.
 The concrete strength is between 25 MPa to 45 Mpa.
 Reinforcing steel strength is between 400 MPa to 500 Mpa.

44. 44
Design procedure
1. Calculate factored axial load Pu
2. Select reinforcement ratio
3. Concrete strength = 30 MPa, steel yield strength = 420 MPa
4. Calculate gross area
5. Calculate area of column reinforcement, As, and select rebar
number and size.

45. 45
Guidelines for Column
Reinforcement
 Long Reinforcement
 Min. bar diameter Ø12
 Min. concrete covers 40 mm
 Min. 4 bars in case of tied rectangular or circular
 Maximum distance between bars = 250 mm
 Short Reinforcement ( Stirrups)
 Least of:
 (16)×diameter of long bars
 least dimension of column
 (48)×diameter of ties
dc
S
Asp

46. 46
Reinforcement of Columns