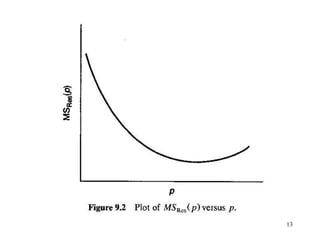
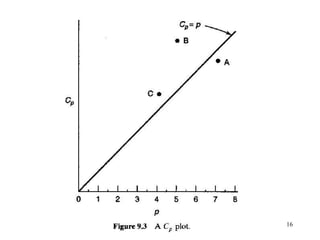
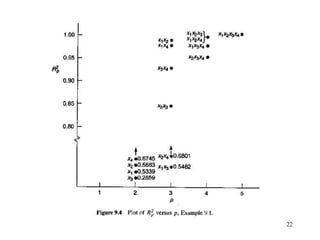
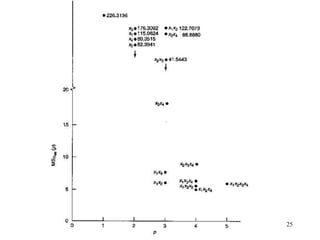
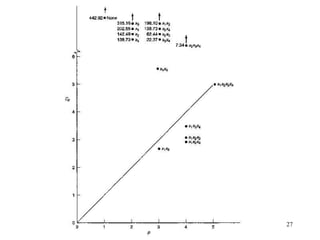
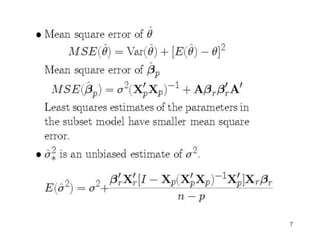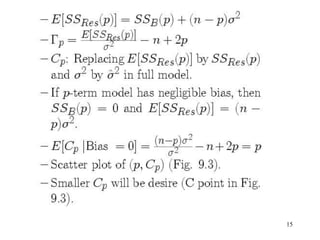This document discusses variable selection and model building techniques. It introduces the variable selection problem of balancing including more variables for information versus fewer variables to reduce variance. Several variable selection algorithms are presented but may select different subsets. Iterative approaches are recommended to check model assumptions. Variable selection aims to improve precision but can introduce bias if unimportant variables are removed. Common evaluation criteria like R-squared and mean squared error are covered. Computational techniques like all-possible regressions, forward selection, backward elimination, and stepwise regression are described.

1. 1
Chapter 9 Variable Selection and
Model building
Ray-Bing Chen
Institute of Statistics
National University of Kaohsiung

2. 2
9.1 Introduction
9.1.1 The Model-Building Problem
• Ensure that the function form of the model is
correct and that the underlying assumptions are
not violated.
• A pool of candidate regressors
• Variable selection problem
• Two conflicting objectives:
– Include as many regressors as possible: the
information content in these factors can
influence the predicted values, y

3. 3
– Include as few regressors as possible: the
variance of the prediction increases as the
number of the regressors increases
• “Best” regression equation???
• Several algorithms can be used for variable
selection, but these procedures frequently specify
different subsets of the candidate regressors as
best.
• An idealized setting:
– The correct functional forms of regressors are
known.
– No outliers or influential observations

4. 4
• Residual analysis
• Iterative approach:
1. A variable selection strategy
2. Check the correct functional forms, outliers
and influential observations
• None of the variable selection procedures are
guaranteed to produce the best regression
equation for a given data set.

5. 5
9.1.2 Consequences of Model Misspecification
• The full model
• The subset model

6. 6

7. 7

8. 8

9. 9
• Motivation for variable selection:
– Deleting variables from the model can improve
the precision of parameter estimates. This is
also true for the variance of predicted response.
– Deleting variable from the model will introduce
the bias.
– However, if the deleted variables have small
effects, the MSE of the biased estimates will be
less than the variance of the unbiased estimates.

10. 10
9.1.3 Criteria for Evaluating Subset Regression
Models
• Coefficient of Multiple Determination:

11. 11
– Aitkin (1974) : R2-adequate subset: the subset
regressor variables produce R2 > R2
0

12. 12

13. 13

14. 14

15. 15

16. 16

17. 17
• Uses of Regression and Model Evaluation Criteria
– Data description: Minimize SSRes and as few
regressors as possible
– Prediction and estimation: Minimize the mean
square error of prediction. Use PRESS statistic
– Parameter estimation: Chapter 10
– Control: minimize the standard errors of the
regression coefficients.

18. 18
9.2 Computational Techniques
for Variable Selection
9.2.1 All Possible Regressions
• Fit all possible regression equations, and then
select the best one by some suitable criterions.
• Assume the model includes the intercept term
• If there are K candidate regressors, there are 2K
total equations to be estimated and examined.

19. 19
Example 9.1 The Hald Cement Data

20. 20

21. 21
• R2
p criterion:

22. 22

23. 23

24. 24

25. 25

26. 26

27. 27

28. 28

29. 29
9.2.2 Stepwise Regression Methods
• Three broad categories:
1. Forward selection
2. Backward elimination
3. Stepwise regression

30. 30

31. 31
Backward elimination
– Start with a model with all K candidate
regressors.
– The partial F-statistic is computed for each
regressor, and drop a regressor which has the
smallest F-statistic and < FOUT.
– Stop when all partial F-statistics > FOUT.

32. 32
Stepwise Regression
• A modification of forward selection.
• A regressor added at an earlier step may be
redundant. Hence this variable should be dropped
from the model.
• Two cutoff values: FOUT and FIN
• Usually choose FIN > FOUT : more difficult to add a
regressor than to delete one.