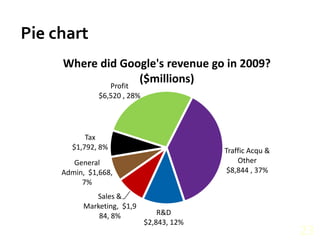
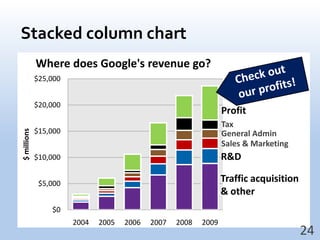
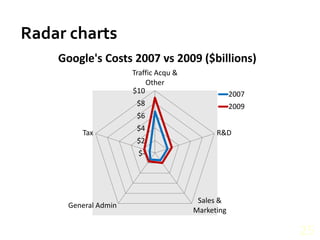
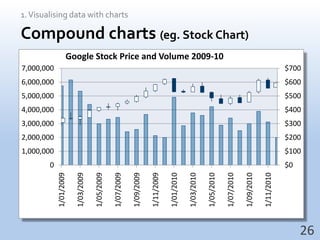
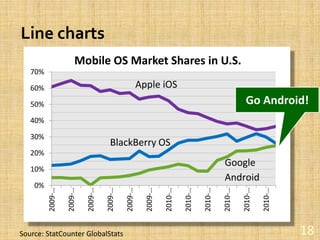
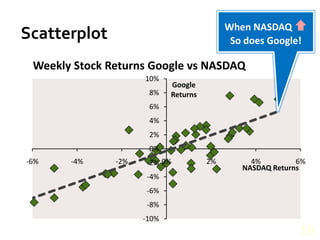
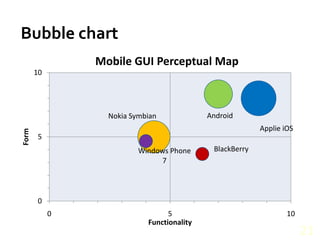
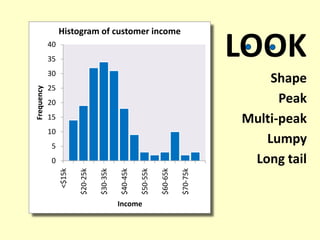
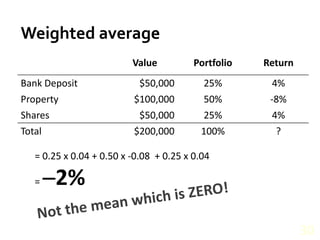
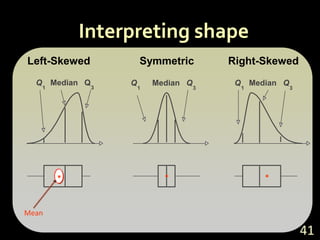
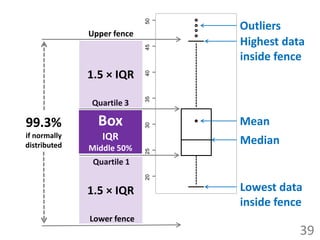
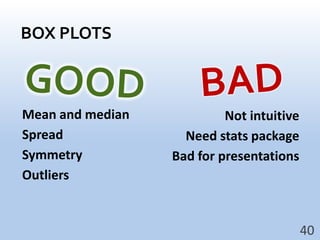
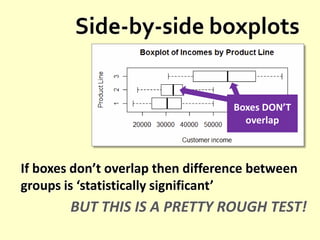
This document provides an overview of key concepts for understanding data, including: - Visualizing data through various chart types like bar charts, line charts, scatterplots, and histograms to build understanding and identify patterns. - Calculating and interpreting the mean, median, and spread of data using concepts like the interquartile range. - Using histograms and box plots to visualize the distribution and spread of data. 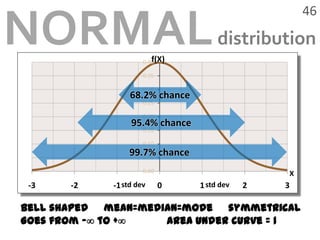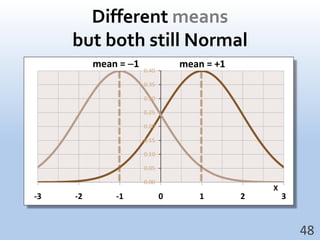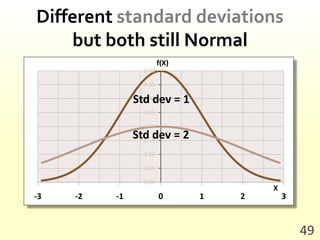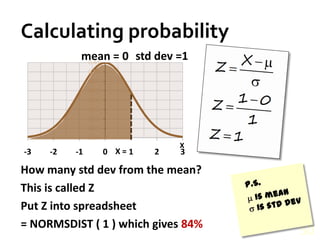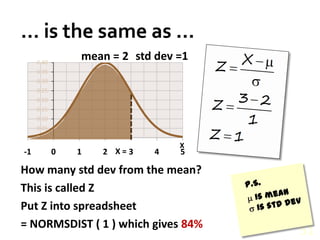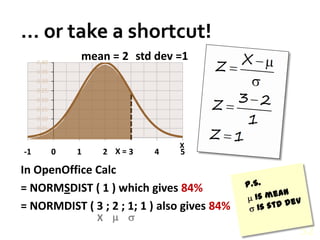- The properties of the normal distribution and how to calculate probabilities based on the mean and standard deviation. 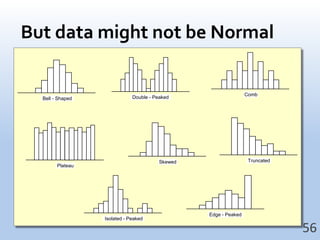The document cautions that real-world data may not always conform to a normal distribution and introduces the central limit theorem. Exercises are provided in R to reinforce these concepts.

1. Not Waving But DrowningUnderstanding DataAndrew Hingstonswitchsolutions.com.au

2. Not Waving But Drowningby Stevie SmithNobody heard him, the dead man,But still he lay moaning:I was much further out than you thought And not waving but drowning.Poor chap, he always loved larkingAnd now he's deadIt must have been too cold for him his heart gave way,They said.Oh, no nono, it was too cold always(Still the dead one lay moaning)I was much too far out all my lifeAnd not waving but drowning. Name and what you doHobby others don’t knowWaving or drowning in data?

3. 3Whyunderstanddata?

4. 4Sometimes we are like this

5. 5… and other times like this!

6. MemorabilityAnchoring and adjustmentStatus quoSelf-servingNegative comparisonsFramingBIAS6

7. Sources of POWERLegitimate powerReferent powerExpert powerReward powerCoercive powerFrench and Raven (1959)“The bases of social power”See Wikipedia:“Power (philosophy)”7

8. PersuasionReciprocityConsistencySocial proofAuthorityLikingScarcityRobert Cialdini (2001)“Influence: Science and practice”See Wikipedia “Robert Cialdini”8

9. Busting jargon9

10. Steps …Specify problemPropose answersIdentify the right toolsObtain your dataVisualise itCrunch numbersInterpret, persuade, apply10

11. Today1. Visualising data2. Measuring middle3. Measuring spread4. Histograms5. Box plots6. Bell-shaped curves7. Exercises using R11Course1. Understanding data2. Monitoring processes3. Exploring relationships

12. 121Visualising

13. Why visualise your data?For youFast understandingBuild solid ‘foundation’Flags problems13For othersEasier to followMemorableLess info overloadMore convincing

14. 14GOODCHARTSBADCHARTS

15. Lots of charts …15

16. Bar charts16Most revenueis still from ads

17. Column charts17And that storygoes back a while

18. Line charts18Go Android!Source: StatCounterGlobalStats

19. Scatterplot19When NASDAQ So does Google!

20. GUI Shoot Out20iOSWin Phone 7SymbianAndroidBlackBerryOSScore out of 10FormFunctionality

21. Bubble chart21

22. 22

23. Pie chart23

24. Stacked column chart24Check outour profits!TaxGeneral AdminSales & MarketingR&DTraffic acquisition& other

25. Radar charts25

26. Compound charts (eg. Stock Chart)261. Visualising data with charts

27. PRESENTATIONS!5 second ruleSimplicityColourFont sizeHandoutsJargonPictures27

28. 282Middle

29. Mode = 1Median = 3Mean = 4Trimmed Mean = 329

30. Weighted average30= 0.25 x 0.04 + 0.50 x -0.08 + 0.25 x 0.04 = 2%Not the mean which is ZERO!

31. 313Spread

32. 32

33. 334Histograms

34. 34LOOKShapePeakMulti-peakLumpyLong tail

35. FreedmanDiaconisEquationSuggests good bin widthVery robustUse common sense though!35IQR = interquartile range, n = data points

36. Double - PeakedBell - ShapedCombPlateauSkewedTruncatedEdge - PeakedIsolated - PeakedWhat is the story?36

37. HISTOGRAMSVisualise spreadEasy to interpretIndicates skewnessIndicates multiple peaks37BADGOODData points?Width of bins?Sample size?

38. 385Box plots

39. 3950454035302520OutliersUpper fenceHighest datainside fence1.5 × IQRQuartile 3BoxIQRMiddle 50%Mean99.3%if normallydistributedMedianQuartile 11.5 × IQRLowest datainside fenceLower fence

40. BOX PLOTSMean and medianSpreadSymmetryOutliers40BADGOODNot intuitiveNeed stats packageBad for presentations

41. Interpreting shape41Right-SkewedLeft-SkewedSymmetricQMedianQQMedianQQMedianQ131313***Mean

42. Side-by-side boxplotsIf boxes don’t overlap then difference between groups is ‘statistically significant’BUT THIS IS A PRETTY ROUGH TEST!42Boxes DON’Toverlap

43. Why?VisualiseMiddleSpreadHistogramsBoxplotsRecap43

44. 446Bell-shapedcurves

45. WARNING!45

46. 46NORMALdistribution68.2% chance95.4% chance99.7% chancestddevstddevBell shaped mean=median=mode symmetricalGoes from - to + Area under curve = 1

47. Mean return 10%Std deviation 10%Likelihood of -50%47?

48. Different meansbut both still Normal48mean = 1mean = +1

49. Different standard deviationsbut both still Normal49Stddev = 1Stddev = 2

50. Calculating probability50stddev =1mean = 0X =How many stddev from the mean?This is called ZPut Z into spreadsheet= NORMSDIST ( 1 ) which gives 84%P.S. is mean is stddev

51. … is the same as …51stddev =1mean = 2X =How many stddev from the mean?This is called ZPut Z into spreadsheet= NORMSDIST ( 1 ) which gives 84%P.S. is mean is stddev

52. … or take a shortcut!52stddev =1mean = 2X =In OpenOfficeCalc= NORMSDIST ( 1 ) which gives 84%= NORMDIST ( 3 ; 2 ; 1; 1 ) also gives 84%P.S. is mean is stddevX

53. NEVERCALCULATE THE PROBABILITYOF ONE POINT53YOU CAN ONLY CALCULATE PROBABILITY OF A REGION

54. SPEED challenge54

55. WARNING!55

56. Double - PeakedBell - ShapedCombPlateauSkewedTruncatedEdge - PeakedIsolated - PeakedBut data might not be Normal56

57. Central Limit TheoremThe shape of the data doesn’t matter … if you take a large enough sample ( > 30 ) the means of the sample will follow a Normal distribution shape around the mean of the underlying data57DEMO

58. Use modified Z-score formula for probabilitythat mean of a sampletakes on certain values58 is mean is stddevn is sample sizeUse Z-score formulaif your data follows aNormal distribution

59. 597Exercises

60. PROJECT60

61. Exercises in RTest DataExercise 4 Employee ExpensesExercise 5 Toll BoothExercise 6 Cycle WorldExercise 9 Chan’s LinenExercise 10 Stock returnsFor the brave!Exercise 11 Social Insight TestExercise 13 QualityExercise 16 Car production61

62. THANKSFeedback please!62