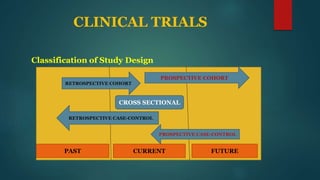
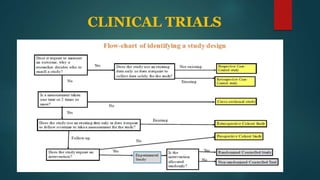
This document provides an overview of clinical trials and statistics. It discusses key concepts like randomized controlled trials, bias, standard deviation, p-values, confidence intervals, risk, odds ratios, and numbers needed to treat. The objectives are to help understand how to interpret clinical trial results and appreciate statistically significant versus clinically meaningful differences. Understanding basic statistics is important for critically evaluating the medical literature and making evidence-based clinical decisions.

1. UNDERSTANDING
CLINICAL TRIALS
STATISTICS
DR.MAGDY KHAMES ALY
CRITICAL CARE MEDICINE
ZMH ALBATAYEH

2. OVERVIEW
 Clinicians examine and intervene with individual patients, must take
clinical decision on a sold base according to guidelines that evidence-
based.
 Statistical analysis is one of the foundations of evidence-based clinical
practice, a key in conducting new clinical research and in evaluating
and applying prior research.
 Reading and getting through clinical trials and researches is most
important part in our daily practice.
 Understanding basic statistical concepts will allow you to become a
more critical consumer of the medical literature, and ultimately be
able to produce better research and make better clinical decisions.

3. OBJECTIVES
 Describe how to interpret the results of a trial, including what
statistical significance means.
 Appreciate that results of trials have a direction, size, and
statistical significance
 Understand the information provided by P values and
confidence intervals
 Know how to interpret statistical significance
 Appreciate when there is an important difference between the
treatment and control arms of a trial.

4. CLINICAL TRIALS
Classification of Clinical trails:
Experimental(Intervention)
Randomized Controlled Trials (RCT)
Non-randomized Trials
 Epidemiologic
Observational
Cohort studies
Case-control studies
Cross-sectional studies
 Non-epidemiologic: Case-study （Case-series）
Opinion from a specialist based on biological and clinical principles
Importance
as
an evidence

5. CLINICAL TRIALS
Classification of Study Design
CROSS SECTIONAL
PROSPECTIVE COHORT
RETROSPECTIVE CASE-CONTROL
RETROSPECTIVE COHORT
PROSPECTIVE CASE-CONTROL
PAST CURRENT FUTURE

6. CLINICAL TRIALS
CONCEPTS AND TERMINOLOGY:
Cohort:
A group of people who share a common characteristics, sample subjects without
knowing their outcome status.
Case-Control Study:
Need to know who has an outcome when deciding which subjects to include in a
study.
Follow to observe their outcome
Compare their exposure status

7. CLINICAL TRIALS
COHORT STUDY CASE-CONTROL STUDY
Smoker Non-smoker With Lung Cancer Without Lung Cancer
N= 4000 N=4000 N=200 N=200
Lung CA - Lung CA + Lung CA - Lung CA + Non-smoker Smoker Non-smoker Smoker
N= 3800 N=200 N=3950 N=50 N=40 N=160 N=180 N=20

8. CLINICAL TRIALS

9. CLINICAL TRIALS
BIAS
 Bias is the intentional or unintentional adjustment in the
design and/or conduct of a Clinical trial, and analysis and
evaluation of the data that may affect the results.
Bias may affect the results of a clinical trial and cause them to be
unreliable.
Bias can occur at any phase of research, e.g. during trial design,
data collection, data analysis and publication.

10. CLINICAL TRIALS
MAJOR TYPES OF BIAS:
 Selection bias
Occurs when the selection of subjects into a sample or their allocation to a treatment group
produces a sample that is not representative of the population, or treatment groups that are
systematically different
prevented by random selection and random allocation
 Detection bias
Occurs when observations in one group are not sought as diligently as in the other
prevented by observer blinding
 Observer bias
Occurs when the observer is able to be subjective about the outcome
prevented by observer blinding and outcome measure design

11. CLINICAL TRIALS
MAJOR TYPES OF BIAS:
 Recall bias
Occurs when patients know which group they have been allocated to,
Which influences the way they report past history and symptoms
ie. if patient knows the are in the placebo group they may exaggerate their ‘untreated’ symptoms
Prevented by patient blinding
 Response bias
Occurs when patients who enroll in a trial may not represent those of the population as a whole
ie. the obese patients who enroll in a weight loss medication trial may be more motivated than those
in the general population
Prevention -> random sampling from population

12. CLINICAL TRIALS
MAJOR TYPES OF BIAS:
 Publication bias
Occurs because negative studies less likely to be submitted and/or published than positive ones
prevented by clinical trials registries and ensuring all well conducted studies are submitted and published (should be
mandatory)
in meta-analysis, the possibility of absent negative studies should be sought for by funnel plot analysis
 Regression to the mean
Occurs when random effects may cause a rare, extreme variation on a measurement if the measurement is repeated, the
likelihood is that the measurement will be less extreme thus, if a treatment had been given after the first measurement, it would
erroneously appear, on the basis of the second measurement, that it had had an effect
prevented by having a control group
 Hawthorne effect
Occurs when the process of studying and following up patients itself influences the outcome
ie. chronic headache may improve in patients who are being studied and regularly followed up
prevented by having a control group and masking the intention of study from patients and observers

13. Biostatistics
Tools used to
Analyze
Present
InterpretMake clinical decisions
Collect
Organize

14. Biostatistics
TYPES OF STATISTICS:
 To Organize Use information from
 Display descriptive statistics to
 Describe data using tables, make decisions or predictions
graphs about a population
Descriptive Inferential

15. Biostatistics
 STANDARD DEVIATION
 HOW TO USE SD
 PROBABILITY: (P value)
 CONFIDENCE INTERVAL
 ODDS AND ODDS RATIO
 RISK AND RISK RATIO
 CALCULATE NNT
 HOW TO INTERPRET A CLINICAL TRIAL

16. Biostatistics
STANDARD DEVIATION(SD):
Standard deviation (SD) is used for data which are “normally distributed” , to
provide information on how much the data vary around their mean.
SD indicates how much a set of values is spread around the average.
A range of one SD above and below the mean
 (abbreviated to ± 1 SD) includes 68.2% of the values.
 ± 2 SD includes 95.4% of the data.
 ± 3 SD includes 99.7%.
 Bell shaped curve when normally distributed

17. Biostatistics
STANDARD DEVIATION(SD):

18. Biostatistics
STANDARD DEVIATION(SD):
SD should only be used when the data have a normal distribution. However,
means and SDs are often wrongly used for data which are not normally
distributed.
A simple check for a normal distribution is to see if 2SDs away from the mean
are still within the possible range for the variable.
For example, if we have some length of hospital stay data with a mean stay of
10 days and a SD of 8 days then:
mean – (2 × SD) = 10 – (2 × 8) = 10 – 16 = –6 days.
This is clearly an impossible value for length of stay ( out of range), so the
data cannot be normally distributed. The mean and SDs are therefore not
appropriate measures to use.

19. Biostatistics
MEDIAN AND INTERQUIRTILE RANGE(IQR):
 Median used in case of SKEWED result (not normally distributed)
 IQR: it’s a range of result
Presenting 3 percentages:
25% of results
50% which is the Median
75% of the results

20. Biostatistics

21. Biostatistics

22. Biostatistics
PROBABILITY (P value):
The P (probability) value is used when we wish to see how likely a hypothesis
is true. The hypothesis is usually that there is no difference between two
treatments, known as the “null hypothesis”.
Null hypothesis:
The Original rule of any comparison or testing something is that no difference
or no effect, the role of biostatistics and P value is to disprove that. Null
hypothesis is impossible to prove it only can be disproved.
You can say that the Null hypothesis not true and there is difference between
two treatment.
The question the P value try to answer is this difference is significant and I
can depend on to make clinical decision or not.

23. Biostatistics
 The P value gives the probability of any observed difference have happened by
chance (the probability of play of chance)
 P = 0.5 means that the probability of a difference this large or larger have
happened by chance is 0.5 in 1, or 50:50.
 P = 0.05 means that the probability of a difference this large or larger have
happened by chance is 0.05 in 1, i.e. 1 in 20.
 The lower the P value, the less likely it is that the difference happened by chance
and so the higher the significance of the finding.
 P = 0.01 is often considered to be “highly significant”. It means that a difference
of this size or larger will only have happened by chance 1 in 100 times. This is
unlikely, but still possible.
 P = 0.001 means that a difference of this size or larger will have happened by
chance 1 in 1000 times, even less likely, but still just possible. It is usually
considered to be “very highly significant”.

24. Biostatistics
Pit falls of P-value:
 P-value becomes larger with a smaller difference.
 P-value becomes larger with a smaller sample size.
Thus, we cannot really tell why statistical significance is absent, due to small effect, or
small sample size?
 Not to confuse statistical significance with clinical relevance. If a study is too small,
the results are unlikely to be statistically significant even if the intervention actually
works.
 Conversely a large study may find a statistically significant difference that is too
small to have any clinical relevance.

25. Biostatistics
In this table we can say that the admission APACHII score and Antibiotic delay have
HIGH STATISTICALLY SIGNIFCANT impact on hospital mortality

26. Biostatistics
Confidence intervals CI:
Confidence intervals (CI) are typically used when, instead of simply
wanting the mean value of a sample, we want a range that is likely to
contain the true population value. This “true value” is the mean value that
we would get if we had data for the whole population.
Statisticians can calculate a range (interval) in which we can be fairly sure
(confident) that the “true value” lies.

27. Biostatistics
Relationship between p-value and 95% Confidence Interval, CI:
95% CI including the null value P>0.05 No difference detected
95% CI excluding the null value P<=0.05 A difference detected
Null value = 1 when a ratio between two means (or proportions) is evaluated.
Null value = 0 when a difference between two means is evaluated.

28. Biostatistics

29. Biostatistics
SD and CI:
Standard deviation tells us about the variability (spread) in a sample. The CI
tells us the range in which the true value (the mean if the sample were
infinitely large) is likely to be. Use SD to describe sampled data, and use 95%
CI to make statistical inference.
Meta-analysis CI 95% graph:
A technique for bringing together results from a number of similar
studies to give one overall estimate of effect.

30. Biostatistics
Risk and Risk ratio(RR):
Risk:
Is the probability that an event will happen.
It is calculated by dividing the number of events by the number of people at risk.
E.g: if 2 from 10 patients taking aspirin will bleed so the Risk of bleeding is 2/10=0.2
Risk Ratio(RR):
Risk in treatment group divided by Risk in controlled group (to compare the 2 Risks)
If RR > 1 that means the Risk increased in treatment group
If RR < 1 that means the Risk increased in control group
If RR = 1 means no difference.

31. Biostatistics
Odds and Odds ratio:
Odds:
Used by epidemiologists in studies looking for factors which do harm, it is a way of
comparing patients who already have a certain condition (cases) with patients who
do not (controls) – a “case–control study”.
calculated by dividing the number of times an event happens by the number of
times it does not happen.
E.g: 2 of 10 patients taking aspirin have bleeding Odds is 2/8=0.25
Odds ratio:
Calculated by dividing the odds of having been exposed to a risk factor by the odds in
the control group.

32. Biostatistics
Odds ratio:
An odds ratio of 1 indicates no difference in risk between the groups, i.e. the
odds in each group are the same.
If the odds ratio of an event is >1, the rate of that event is increased in patients
who have been exposed to the risk factor.
If <1, the rate of that event is reduced.

33. Biostatistics
Risk reduction and numbers needed to treat(NNT):
Risk reduction:
It refer to Relative or Absolute Risk Reduction(RRR,ARR) and it answer and
quantify how often the treatment or intervention works?
ARR is the difference between the event rate in the intervention group and that in
the control group. It is usually given as a percentage.
RRR is the proportion by which the intervention reduces the event rate. It is
calculated by dividing the ARR by the control event rate.
NNT is the number of patients who need to be treated for one to get benefit.
It is 100 divided by the ARR, i.e. NNT = 100/ARR

34. Biostatistics
Risk reduction and numbers needed to treat(NNT):
In a study testing the effect of a new antihypertensive patients 100 patient have been given the
new treatment and another 100 have been given placebo and followed up for 1 month the results
shown:
 ARR : (improved drug group – improved placebo group): 80%-60%=20% so ARR=20%
 NNT: (100/ARR) 100/20=5 so we need at least 5 patient taking the drug to see the effect in
1 of them.
 RRR: (ARR/event or not improved in Control group) 20/40=0.5 so RRR is 50% by this drug
Antihypertensive group Placebo group
Improved Not improved Improved Not improved
80 20 60 40

35. SUMMARY
 Mean and Standard deviation are useful when data are normally distributed,
otherwise, you may consider using Median and Inter-quartile range because they
are more robust for data distribution.
 P-value indicates the probability of falsely detecting a difference when there is no
difference. Larger effect and larger sample size leads to more significant result
(smaller p-value). So even clinically meaningless difference could reach statistical
significance, so be careful.
 Using confidence interval can refer statistical significance. When 95% CI does not
include null value, which links with P < 0.05.
 Use SD to describe sampled data, and use 95% CI to make statistical inference.
 Biostatistics are important topic to learn if you keen to be up-to-date with medical
researches and literatures

36. References
 Harris M, Taylor G, Dunitz M. Medical Statistics Made Easy. London and New York: 3rd
edition; 2014.
 Altman DG, Bland JM. Absence of evidence is not evidence of absence. BMJ
1995;311(7003):485.
 Higgins JP, Thompson SG, Deeks JJ, Altman DG. Measuring inconsistency in meta-
analyses. BMJ 2003;327(7414):557-60.
 Barratt A, Wyer PC, Hatala R, et al. Tips for learners of evidence-based medicine: 1.
Relative risk reduction, absolute risk reduction and number needed to treat. CMAJ
2004;171(4):353-8.
 Cates C. P values and confidence intervals (Update Article 2005). [Full text
(http://www.nntonline.net/pvalues-and-confidence-intervals/)]
 Guyatt G, Jaeschke R, Heddle N, Cook D, Shannon H, Walter S. Basic statistics for
clinicians: 1. Hypothesis testing. CMAJ 1995;152(1):27-32.