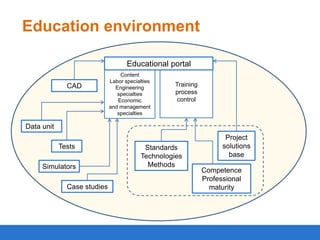
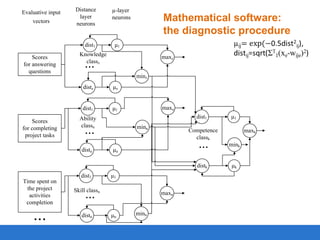
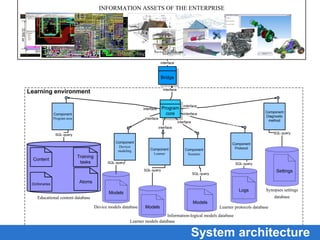
The document proposes an intelligent distance learning environment for engineering education. It introduces individualized learning based on domain, learner, and learning scenario models. The principles of intelligence and individualization are described to improve quality through applying artificial intelligence and forming individual learner trajectories. The principles of integration and accessibility ensure interaction between the environment and enterprise information assets and availability anywhere through cloud computing. Key components of the proposed environment are an educational portal, content management, and a data unit to control the learning process. Mathematical models are provided for the domain, learner, diagnostic procedures, learning scenario, and system architecture. Contact details are given for the research institution developing this environment.

1. Intelligent distance
environment for engineering
education

2. Introduction
Prediction of the educational, learner-oriented process
in the computer-based learning systems provides
the ability to customize it, and as a result, improve
the quality, efficiency and manageability.
The individualization of the learning process is based
on a number of scientific results obtained by the authors:
domain model, learner's fuzzy model, learning scenario,
diagnostic procedures and learning process planning.
The learning content is an experience, which is put
in the learning programs, techniques, methods,
models and practices.

3. The principles of intelligence,
individualization
The principle of intelligence implies that to increase
efficiency and quality of distance e-learning it is necessary
to apply the rich experience of artificial intelligence theory
and practice, including smart- technologies.
The principle of individualization implies that to develop
the required competencies of trainees it is necessary
to form their individual trajectories of engineering
education containing methodological, supervisory
and design pedagogical components.

4. The principles of integration,
accessibility
The principle of integration means the interaction
between educational environment with the enterprise
information assets.
The principle of accessibility implies that m-training
is available for any place , any time and any category
of students (3–For Principle) and is provided
by organizational and technical means of cloud computing.

5. Education environment
Educational portal
CAD
Content
Labor specialties
Engineering
specialties
Economic
and management
specialties
Training
process
control
Data unit
Tests
Simulators
Case studies
Standards
Technologies
Methods
Project
solutions
base
Competence
Professional
maturity

6. Mathematical software:
the domain model
The domain model is given as
SModel = {ObjectName; Functions; Processes;Data; Patterns;
MetaData | ortree;≺; view}; where
ObjectName = {ObjectNamei , i = 1 . . .E} is a set of subject objects names;
Functions = {functioni, i = 1 . . . Z} is a set of subject functions;
Processes = {processi, i = 1 . . .P} is a set of subject processes;
Datat = {datai, i = 1 . . .D} is a set of subject data;
Patterns = {Operationi, Commandi, Methodi, i = 1 . . .T} is a set of subject
templates,
Operation = {operationi, i = 1 . . .O} is a set of subject operations,
Command = {commandi, i = 1 . . .C} is a set of subject commands,
Method = {methodi, i = 1 . . . S} is a set of subject methods to run a command,
Atom = {notioni, actioni, i = 1 . . .A} is a set of knowledge "atoms", consisting of elementary concepts and the simplest actions,
Atom ∈ Stage, Atom ∈ Procedure, Atom ∈ Operation,
Atom ∈ Command, Atom ∈ Method;
MetaData = {keyi, hash-function, i = 1 . . .H} is model metadata,
where <keyi > is a tuple of associative keys,
hash-function is a hash function for element searching;
ortree is an hierarchical relation;
≺ is a relation of the order;
view is an associative relation.

7. Mathematical software:
the learner model
Description of the learner model is given as
UserModel = {OcenkaZnaniei;OcenkaUmeniei;OcenkaNaviki;
OcenkaKompetentnosti; haracteristika | calcZ; calcU; calcN; calcK;
i = 1 …N}; where
OcenkaZnaniei, OcenkaUmeniei, OcenkaNaviki and OcenkaKompetentnosti
are arrays of grades for knowledge, abilities, skills and competence respectively, N is
the number of scenario control points Ki. The range of values of the grade calculation
functions is given in pairs (D, µ): calcZ, calcU, calcN, calcK ∈ (D, µ), where D is a
value of Euclidean distance function, µ is a value of the class characteristic
membership function, haracteristika =
{grade1; grade2; grade3;… ; gradeS} is a set of linguistic characteristics. calcZ:
markTeori →gradei, calcU: marki →gradei, calcN: ti →gradei, calcK: calcZ,
calcU, calcN → gradei where markTeori is a set of grades for the solution of
theoretical problems, marki is a set of grades for the operations completed,
ti is a set of the timeframes which were taken to solve problems.
calcZ, calcU, calcN, calcK functions are implemented with fuzzy Kohonen maps and
the custom developed rating scale in interval and linguistic forms.

8. Evaluative input
vectors
Distance
layer
neurons
dist1
Scores
for answering
questions
µ-layer
neurons
μ1
Knowledge
classz
maxz
...
minz
distz
μz
dist1
Scores
for completing
project tasks
Mathematical software:
the diagnostic procedure
μ1
maxu
dist1
Ability
classu
minu
...
μ1
Competence
classk
maxk
dist1
Time spent on
the project
activities
completion
distn
μu
μ1
Skill classn
...
...
...
maxn
μn
minn
mink
distk
distu
μk

9. Mathematical software:
a model of learning scenario
The model is given as
Scenariy = {G(vertex; edge);Reflaction; Alternativ};where
G (vertex, edge) is a scenario directed graph,
vertex = {vi, i = 1… V} is a set of attribute vertices,
edge = {ei, i = 1 … E} is a set of edges;
Reaction = {Rf1, Rf2, Rf3, Rf4} is a set of heterogeneous vertex
mappings
into the subject objects (Rf1 is the names of subject objects, function
objects,
processes, data, patterns (see the SModel model), Rf2 is the test
questions,
Rf3 is the practical subject tasks, Rf4 is the Ki control points,
containing the
required (target) linguistic criteria characteristics values of the
learner);
Alternativ = {vj , if vi is incidential to vj an vi = Ki, vi ≺ vj} is the
learner's
choice of learning trajectory from vi noncontrol vertex.

10. INFORMATION ASSETS OF THE ENTERPRISE
interface
Bridge
interface
Learning environment
IUnknown
IUnknown
interface
Component
Program area
Program
core
interface
Component
Diagnostic
method
interface
interface
interface
IUnknown
interface
IUnknown
IUnknown
IUnknown
SQL-query
SQL-query
Component
Devices
modeling
Content
Training
tasks
Component
Learner
Component
Scenario
Component
Protocol
SQL-query
SQL-query
SQL-query
Settings
SQL-query
Dictionaries
Atoms
Logs
Models
Synopses settings
database
Educational content database
Models
Device models database
Models
Learner protocols database
Information-logical models database
Learner models database
System architecture

11. Contacts
Ulyanovsk State Technical University,
The Institute of Distance and Further Education.
Engelsa str. 3. 432063, Ulyanovsk, Russia
tel. +7-8422-77-88-45
http://gc.ulstu.ru, http://ido.ulstu.ru
Alexander Afanas’ev, pro-rector for the distance
and further education, UlSTU
E-mail: a.afanasev@ulstu.ru