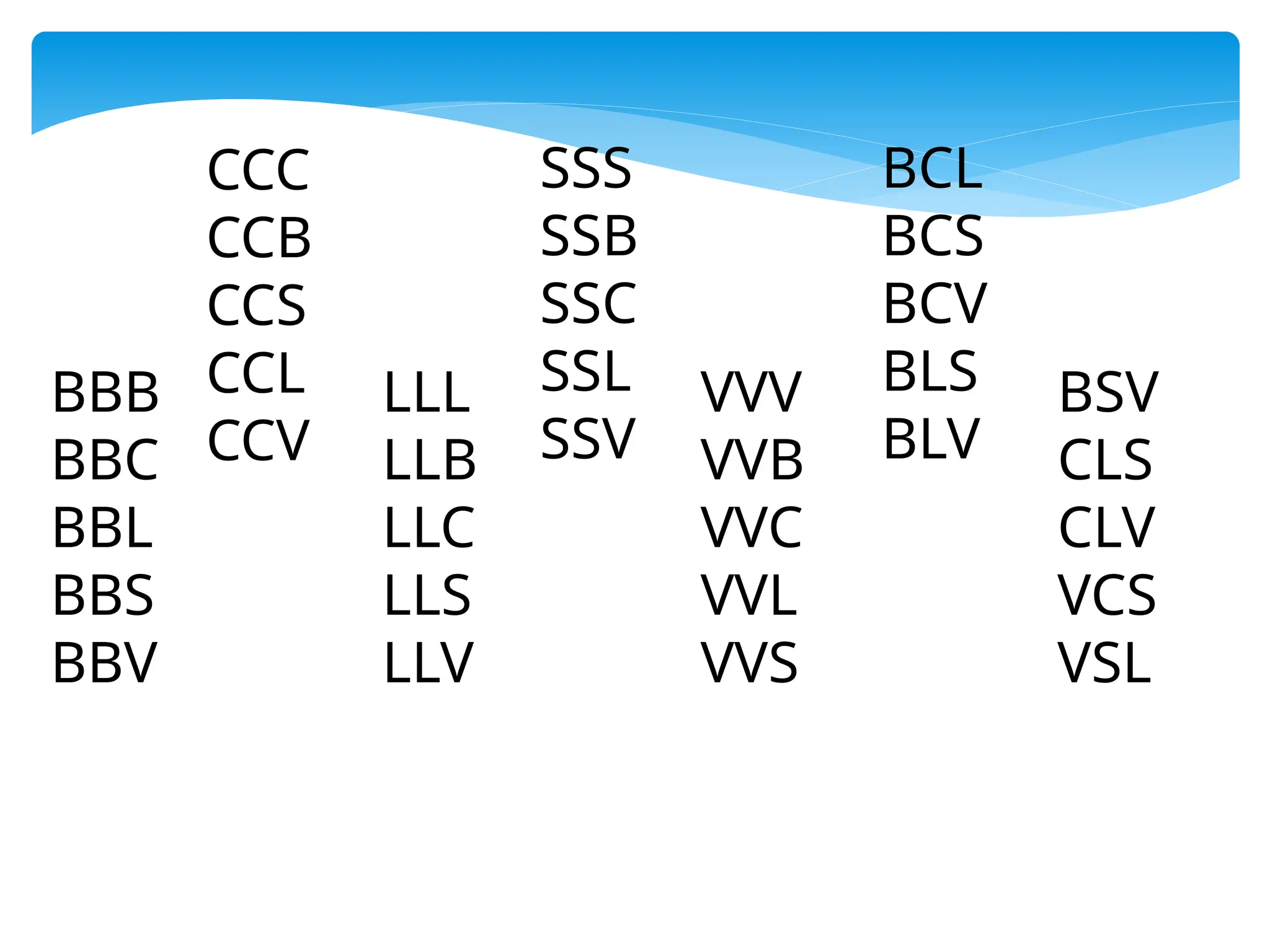
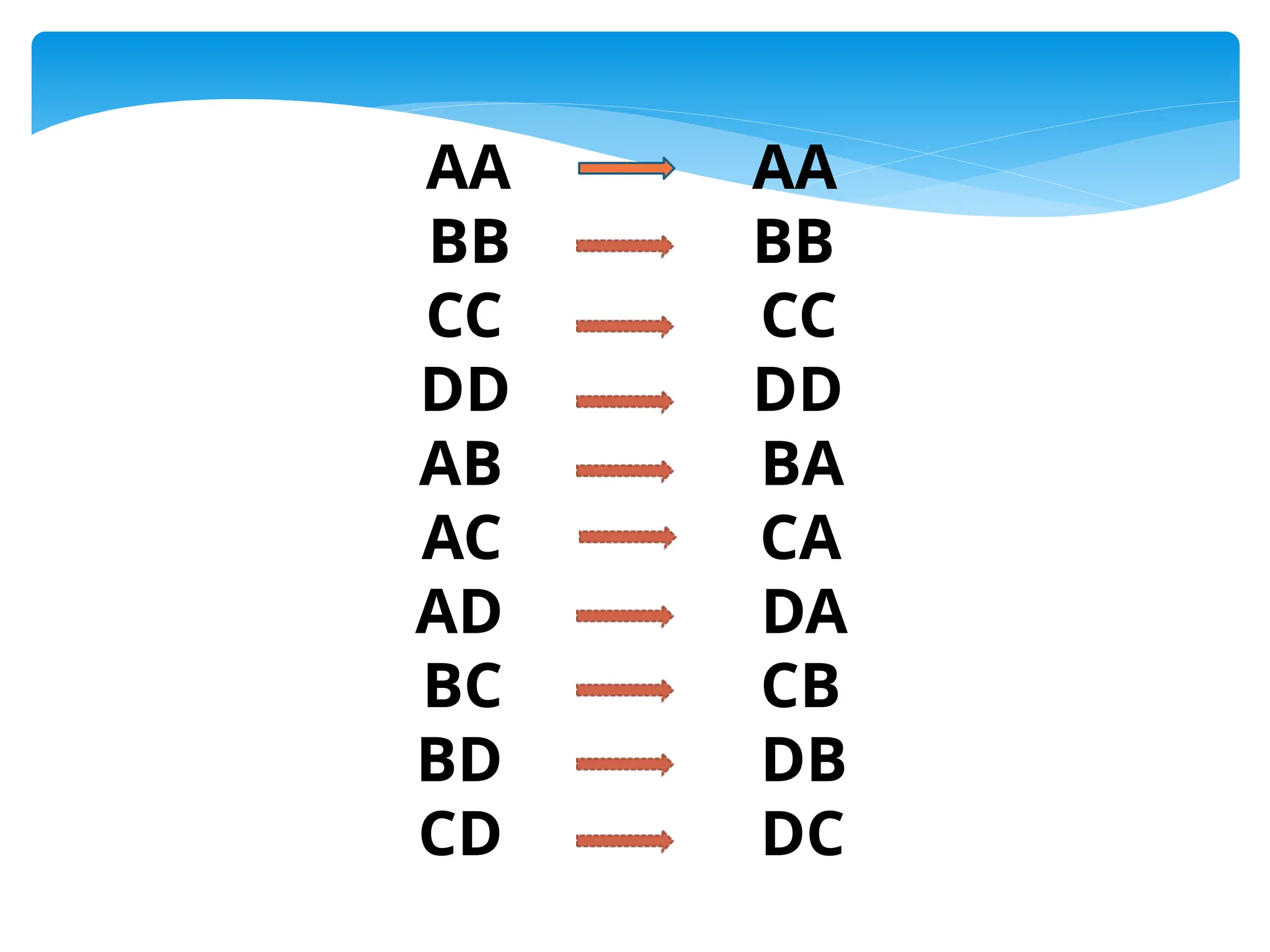
The document explains combinations, distinguishing between those with and without repetition using examples of ice-cream flavors and letter combinations. It provides formulas for calculating combinations based on the number of distinct objects and the number chosen. Examples illustrate how to derive the number of variations and different words that can be formed.

1. COMBINATION

2. A combination of a set of distinct objects
is an unordered selection of elements from
the set

3.  COMBINATION WITH
REPETITION
 COMBINATION WITHOUT
REPETITION
THERE ARE BASICALLY 2 TYPES OF COMBINATION

4. Ex.
Let us say there are five flavors of ice-cream: banana, chocolate,
lemon, strawberry and vanilla. You can have three scoops. How
many variations will there be?
Let's use letters for the flavors: {b, c, l, s, v}
Problem:
How many 3-scoop ice-cream set will
be created out of five flavors?

5. Solution:
=
¿
7 !
3 ! ( 4) !
7𝑥 6 𝑥5 𝑥 4 𝑥3 𝑥2 𝑥1
3𝑥 2𝑥1(4 𝑥 3𝑥 2𝑥1)
¿
5040
6( 24)
¿
5040
144
= 35
Given:
n=5
r=3

6. CCC
CCB
CCS
CCL
CCV
BBB
BBC
BBL
BBS
BBV
LLL
LLB
LLC
LLS
LLV
SSS
SSB
SSC
SSL
SSV
VVV
VVB
VVC
VVL
VVS
BCL
BCS
BCV
BLS
BLV
BSV
CLS
CLV
VCS
VSL

7. EX.
How many different 2-letter words
can be created from 4 distinct
letters such as a, b, c and d?
COMBINATION WITH REPETITION:

8. Using the formula
Given: n=4
r=2
¿
5 !
2 !(3) !
¿
120
12
¿10
where n is the number of things
to choose from, and you choose
r of them
(Repetition allowed, order
doesn't matter)

9. AA AA
BB BB
CC CC
DD DD
AB BA
AC CA
AD DA
BC CB
BD DB
CD DC

10. Using the formula:
COMBINATION WITHOUT REPETITION
Given: n=4
r=2
¿
4 !
2 ! (4 − 𝑟 ) !
¿
4 !
2 ! (2)!
4 𝑥 3𝑥 2 𝑥 1
2 𝑥 1(2 𝑥 1)
¿
24
4
=6
where n is the number of things
to choose from, and you choose
r of them
(No repetition, order doesn't
matter)